基于博弈演化算法的PMU最优配置方法

毛 义，吕飞鹏

（四川大学 电气信息学院，四川 成都 610065）

0 引言

基于GPS或北斗和离散傅里叶变换DFT（Discrete Fourier Transform）原理的同步相量测量单元PMU（Phasor Measurement Unit）在广域测量系统WAMS（Wide Area Measurement System）中扮演着核心角色［1-4］。随着对电力系统状态评估和安全评估要求的不断提高，基于数据采集与监视控制（SCADA）系统的数据采集和处理亟待技术上的提升［5-6］。电力系统中所有PMU与一个GPS或北斗时钟以微秒级误差实现同步，可以直接测量节点电压相量幅值和相角，并通过高速通信信道把数据传输到调度中心［7］。国网公司正在加快WAMS的建设，目前500 kV及以上变电站、220 kV主要变电站、100 MW以上机组和新能源并网汇集站几乎均安装了PMU。

由于PMU的高成本，众多学者都在寻求PMU最优配置OPP（Optimal PMU Placement）方法。在解决OPP问题上，已有优化算法主要包括确定性分析法［8-10］和启发搜索法［11-13］两大类。文献［8］使用二进制粒子群算法优化配置PMU，将PMU数量与不可观节点作为适应度参数，使其满足种群的最大适应度。文献［9-10］使用数字规划算法建立不等式约束方程求解结果。确定性分析法通过建立不等式约束求解问题，结果单一、效率低、计算量大，不适合解决大型网络优化问题。文献［11］提出使用遗传算法解决OPP问题，并分析了系统发生故障的情况。文献［12］研究了基于禁忌算法配置PMU，并考虑了最大冗余度问题。文献［13］使用模拟退火混合遗传算法解决PMU优化配置问题。启发搜索法使用某种规律随机搜索最优解，搜索方向不确定，全局最优解难以得到保证，易早熟或收敛于局部最优解。

博弈论作为一个先进的优化工具［5］，越来越受到学术界的重视。博弈论源于经济学，研究多个利益相关主体如何进行优化决策，其在军事、社会科学、工程等领域有着广泛的应用，在智能电网快速发展的过程中，博弈论为其优化问题提供了新的解决途径。本文以电力系统状态完全可观和PMU配置数量最少为目标，提出了一种基于博弈论［5］的演化优化算法。电力系统一个节点可映射为经济学中一个理性人，PMU最优化配置问题可映射为理性人的博弈过程，最优配置方案对应于主体博弈的纳什均衡解。基于博弈论的演化算法演化方向确定，提高了收敛速度和全局搜索能力，对于实际大电网也有收敛性好的特征，而且使PMU的配置问题更加形象、直观。与此同时，算法采用非合作博弈模式，提高了解的多样性，为实际工程提供了更多选择，提高了可操作性。

1 电力系统可观测性

1.1 代数可观性

实现电力系统可观性，可以采用数值分析或网络拓扑方法。一个节点数为N、测量向量维数为m的电力系统，其线性量测模型可表示为：

其中，Z为m维测量向量；H为m×（2N-1）维测量雅可比矩阵；x为2N-1维电压状态向量；E为m维测量噪声向量。代数可观性的理论基础线性量测模型可以直接求解，即如果rank（H）=2N-1，即H满秩，则可认为系统是代数可观的。

1.2 拓扑可观性

从图论的角度，可以将电力系统看成是一个由N个顶点和b条边构成的图G=（V，E），V表示图的顶点集，E表示图的边集合，它们分别对应于系统的母线和支路集合。一个测量子图 G′=（V′，E′），并有V′⊆V，E′⊆E。如果测量网络满足 V⊆V′，即子网络图G′中包含了图G的所有顶点，则系统是拓扑可观的。

2 OPP的数学模型

2.1 OPP目标函数

如果在系统每个节点都安装PMU，则无需迭代计算就可以实现整个系统完全可观性。但由于PMU的高成本，如果在系统的每个节点都安装PMU，则费用太高且没有必要。如何找到最优的安装位置和合理的安装数量是需要解决的问题。n节点系统OPP问题可以由以下目标函数给出：

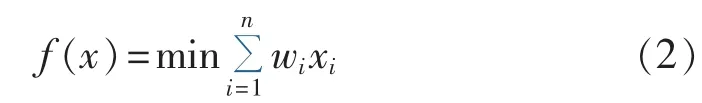
其中，n为给定系统的节点数；wi为在节点i安装PMU的成本，主要包括通信网络、TA、TV、GPS接收器等，本文中不考虑各个节点PMU安装成本差异，wi都假设为1；xi表示节点PMU安装状态，由一个二进制数表示，如式（3）所示。

2.2 可观测性的约束条件

电力系统一个节点是否可观由以下规则来判断。

a.一条已经配置了PMU的母线，其电压及连接到该母线每条支路的电流都能被测量。

b.若支路一端装有PMU，则该支路另一端的节点电压能被虚拟测量。

c.若已知支路两端节点电压，则该支路电流能被虚拟测量。

d.除一条支路外，若其余与某节点相连的所有支路的电流都已知，即支路上的电流能利用基尔霍夫电流定律（KCL）间接计算出来，则未知电流支路的电流能被虚拟测量。该规则适用于一个节点上的电流平衡关系已知的情况。

e.如果节点i为无负荷节点，且节点i的电压相量未知，与节点i相连的所有节点的电压相量已知，则节点i的电压相量可通过计算得到。

根据以上配置原则，系统节点关联矩阵如下：

系统可观测性的约束方程可表示为：

其中，F（X）为一个矢量函数；X=［x1，x2，…，xn］T，表示各个节点PMU配置的状态；A为系统节点关联矩阵；I为所有元素都为1的n维列向量。

3 博弈算法

3.1 映射关系

博弈论是现代数学的一个重要分支，主要研究多个决策主体存在利益联系或冲突时，主体如何根据自身能力及所掌握的信息作出有利于自己或决策者群体的决策。一个博弈［5，14］的基本结构由三元组合表示：

其中，G为参与博弈的理性人，每个参与者的纯策略为有限集；S为策略空间，即纯策略的n元组合；U为支付函数，即理性人的期望。

纳什均衡在非合作博弈分析中有十分关键的作用和地位。纳什在1950年的论文中证明了任何一个有限博弈至少有一个纳什均衡。在博弈B=（G，S，U）中，策略组合为一个纳什均衡，对于任意博弈方，存在是给定其他博弈方情况下 xi的最优策略，即。也即存在一个策略组合，所有博弈方面临同一情况，在其他博弈方不改变策略时，此时的策略是最优策略。

本文通过一个映射关系将PMU的配置寻优过程转化为博弈主体寻找博弈均衡解的过程。每个节点xi映射为一个博弈主体，xi的策略映射为策略组合S的一个变量，目标函数 f（x）映射为博弈主体的支付函数U（S）。映射关系如图1所示。

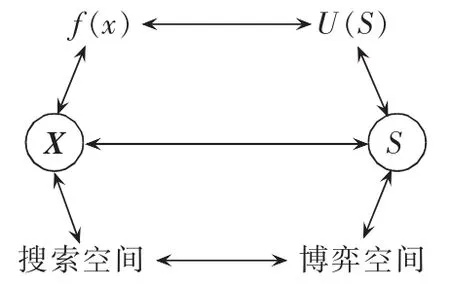
图1 映射关系Fig.1 Mapping relation

3.2 算法说明

在博弈论原理指导下，本文设计一种演化博弈算法（EGA）［15］。算法采用自下而上的设计方式，构造拥有理性人特征的主体，通过主体的利益冲突来寻找纳什均衡解［16］，算法的演化过程可建立一个马尔科夫链模型，再通过扰动因子在均衡解随机扰动后重新寻找均衡解，最终达到全局的帕累托最优解。

本文设计的EGA用一个六元组合表示：

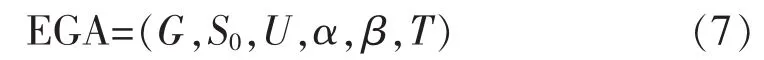
a.博弈结构G。

对于每个主体 xi（i=1，2，…，n）用一个纯策略表示，n个主体的纯策略组合S对应于PMU配置的一个解。

b.初始策略S0。

每个主体xi在自己的策略空间（0或1）中随机选择一个策略组成初始策略S0。

c.支付函数U。

在同一策略组合S下，各行为主体为非合作博弈模型，定义在同一策略下各主体具有相同的支付函数，如下式所示：

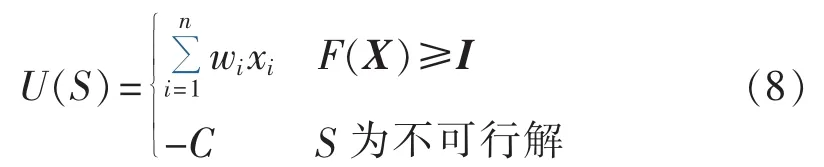
如果S为可行解，支付函数即为所求的目标函数；如果S为不可行解时，C为给予所有主体的惩罚函数［16］。保证无论初始策略如何，在所有主体进行了一次策略调整后，策略S一定收敛于可行解。

d.主体理性行为α。

本文假设所有主体都具有经济理性，即始终追求自身收益的最大化，在博弈演化过程中，主体通过自身策略（0或1）的调整来不断增加自身收益。本文把主体顺序从1到n的一次调整称为一次迭代。如果一次迭代前后主体收益不再变化，即任一主体不能通过单独改变自身策略来增加收益，此时就达到了一个纳什均衡解。

e.均衡扰动因子β。

当各个主体均无法选择更优的策略更新系统状态，系统达到了纳什均衡，但纳什均衡解不一定是帕累托最优解［15］。为了进一步演化，设置扰动因子对均衡策略进行随机扰动，使之偏离均衡解然后再进行新一轮的博弈，不断地重复这样的过程以搜寻到更优的解。对于S的每个主体xi的策略si，如果随机数 rand（0，1）小于扰动因子 β，主体 xi用相反策略代替si，否则策略保持不变。得到新的策略组合S′后，主体在新的策略组合再次进行顺序寻优。

f.最大博弈回合数T。

本文定义寻找到一个纳什均衡解的过程为博弈的一个回合，T为预设的最大博弈回合数。

基于以上对算法的描述，得到算法的流程图如图2所示。

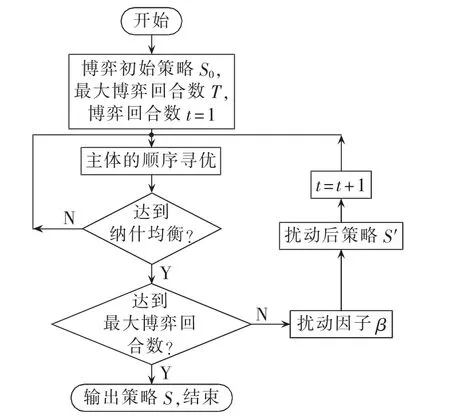
图2 算法流程图Fig.2 Flowchart of algorithm

4 算例结果与比较

利用本文提出的博弈演化算法对IEEE 30、新英格兰39节点系统进行仿真计算，并与深度优化解（DFS）算法、模拟退火（SA）算法以及最小生成树（MST）算法计算的结果进行比较，说明博弈算法的可行性与优点。应用EGA对上海地区128节点系统进行仿真计算，说明算法的实用性并给出配置原则建议。

4.1 算例1

在 IEEE30 节点系统中［12］，节点 6、9、22、25、27、28为无负荷节点。设置扰动因子β分别为0.1、0.5，最大博弈回合数T=1000。分别应用DFS算法、SA算法、MST算法、EGA进行仿真计算，得到结果如表1所示。

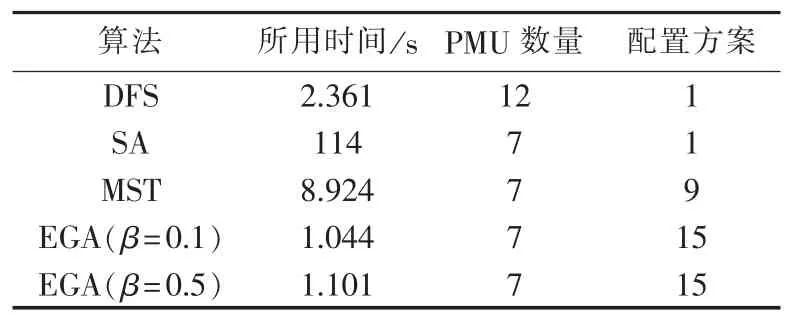
表1 IEEE 30节点系统仿真结果Table 1 Simulative results of IEEE 30-bus system

本文的结果采用MATLAB程序，在CPU主频为2.7 GHz的主机上运行得到。在其他电脑上结果可能不同，但比例关系不变。从表1中可知，DFS算法和EGA的计算速度都很快，但DFS算法的收敛性差，配置PMU的数量是EGA的2倍，其所造成的不必要的冗余会导致经济性能下降。SA算法解的收敛性与初始值有密切的关系，每搜索一步就要计及所有节点配置情况，计算量大、收敛速度慢。MST算法虽在收敛性速度和质量上吸取了DFS、SA算法的优点，但仍是一种随机搜索算法，收敛速度和解的多样性还是不及EGA。从表1也可看出，扰动因子的大小并不影响算法的收敛速度和收敛性。扰动因子大小只影响新的策略组合S′和纳什均衡解的差异程度。但主体会在新的策略组合再次进行顺序寻优，并不影响最终的帕累托最优解。比较而言，EGA利用了理性主体的理性行为，策略信息被所有主体共知，演化方向确定。除了计算约束条件外，最主要的操作就是比较不同策略的效用大小、收敛速度。由于非合作博弈可存在多个纳什均衡解［14］，也保证了解的多样性。

4.2 算例2

新英格兰 39 节点测试系统［18］中，节点 1、2、5、6、9、10、11、14、17、19、22 为无负荷节点。算法设置扰动因子β分别为0.1、0.8，最大博弈回合数T=1000。分别应用DFS算法、SA算法、MST算法、EGA进行仿真计算，得到结果如表2所示。

当系统结构变得更加复杂时，DFS的收敛性差的缺点将更明显，配置的数量几乎是最优解的2倍。而SA算法收敛速度慢的缺点也暴露无遗，对于大系统并不适用。MST算法虽然在解的收敛性、收敛速度和解的多样性上都得到一定的改善，但收敛速度和解的多样性上都远远不及EGA。

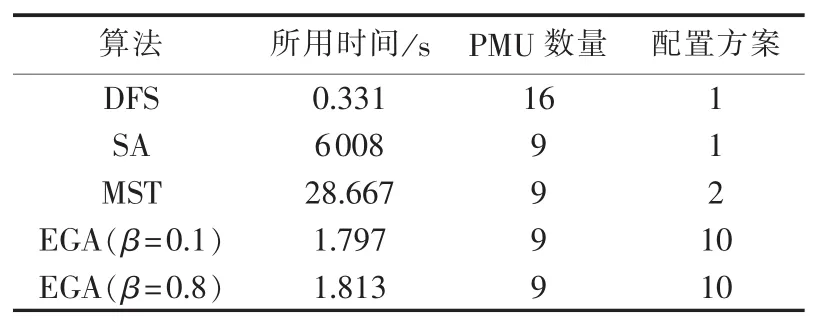
表2 新英格兰39节点系统仿真结果Table 2 Simulative results of New England 39-bus system

4.3 算例3

上海地区220kV以上电网共128个节点，如图3所示。其中，节点1—15、26、27为电源点，节点16—25、95为500 kV变电站，其他节点为220 kV变电站和负荷节点。应用EGA分别在无条件（记为情况1）下进行全网PMU配置，以及在已知所有电源点和500 kV变电站安装PMU的条件（记为情况2）下，对系统其他节点配置PMU，算法设置扰动因子β=0.1，最大博弈回合数T=1000。结果如表3所示。

图3 上海地区128节点系统Fig.3 Shanghai 128-bus system

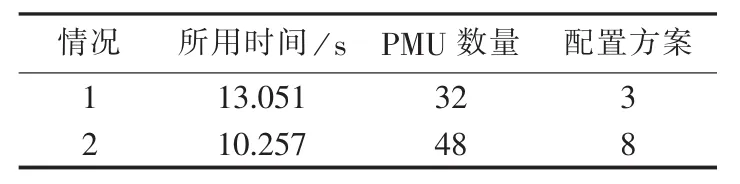
表3 上海电网128节点系统仿真结果Table 3 Simulative results of Shanghai 128-bus system

在实际大系统的仿真中，EGA的收敛速度快和解多样性好的特点得到进一步体现。而且可以看出，当系统结构成几何数量增加时，EGA的收敛速度并不会成几何增加，依然在秒级范围内，更加说明EGA能很好地应用于实际。在已知所有电源点和500 kV变电站安装PMU的条件下，针对其他节点进行配置PMU得到的方案虽然比无条件时多出2倍，但整体所需的PMU数量却比无条件时多出一半。考察其中2种优化配置方案如表4所示。

表4 上海128节点系统配置结果Table 4 PMU configuration of Shanghai 128-bus system

从表4中可知，2种情况下在500 kV枢纽变电站都配置了PMU，在情况2下多出的PMU数量主要是因为对所有电源点配置了PMU，造成了冗余。因此，考虑全网可观测性和经济性，PMU的优化配置应从全网角度进行整体优化配置，PMU配置规划应和电网规划同步进行，并且优先在500 kV枢纽变电站建设。

5 结论

本文提出了一种基于博弈论的演化算法求解PMU最优配置的问题，并通过实例验证了算法的有效性。与常用的DFS、SA、MST算法的结果对比，证明本文算法克服了SA算法的收敛速度慢和DFS算法收敛性差的缺点。与MST算法相比，本文算法收敛速度更快、解多样性更好，可为实际工程建设提供更多的可行性方案，在对实际大系统的仿真中，更体现了本文算法收敛性好与收敛速度快的优点。本文提出了对现行PMU配置原则的建议。

本文以电力系统正常运行的可观测性为目标，未考虑系统N-1状态和通信信道故障时系统的可观测性。在考虑PMU的成本时，也没有考虑各个节点PMU安装成本的差异。系统出现N-1状态或通信信道有限的情况下考虑系统的可观测性的PMU最优化配置将是下一步的研究目标。

参考文献：

［1］李江，徐志临，李国庆.配电网微型PMU与故障录波装置研究与开发［J］.电力自动化设备，2016，36（9）：54-59.LI Jiang，XU Zhilin，LI Guoqing.Research and development of micro PMU and fault wave recording device for distribution network［J］.Electric Power Automation Equipment，2016，36（9）：54-59.

［2］ARIASD，VARGASL，RAHMANN C.WAMS-basedvoltage stability indicator considering real time operation［J］.IEEE Latin America Transactions，2015，13（5）：1421-1428.

［3］LU Chao，SHI Bonian，WU Xiaochen，et al.Advancing China’s smart grid：phasor measurement units in a wide-area management system［J］.IEEE Power and Energy Magazine，2015，13（5）：60-71.

［4］刘新东，江全元，曹一家.N-1条件下不失去可观测性的PMU优化配置方法［J］.中国电机工程学报，2009，29（10）：47-51.LIU Xindong，JIANG Quanyuan，CAO Yijia.Optimal PMU placement to guarantee observability under N-1 condition ［J］.Proceedings of the CSEE，2009，29（10）：47-51.

［5］卢强，陈来军，梅生伟.博弈论在电力系统中典型应用及若干展望［J］.中国电机工程学报，2014，34（29）：5010-5016.LU Qiang，CHEN Laijun，MEIShengwei.Typicalapplications and prospects of game theory in power system［J］.Proceedings of the CSEE，2014，34（29）：5010-5016.

［6］MOSTAFA B M，RAHMAT-ALLAH H，FARIBARZ H F.A new approach for optimal placement of PMUs and their required communication infrastructure in order to minimize the cost of the WAMS［J］.IEEE Transactions on Smart Grid，2016，7（1）：84-93.

［7］彭江南，孙元章，王海风.考虑系统完全可观测性的PMU最优配置方法［J］.电力系统自动化，2003，27（4）：10-16.PENG Jiangnan，SUN Yuanzhang，WANG Haifeng.An optimal PMU placementalgorithm forfullnetwork observability ［J］.Automation of Electric Power Systems，2003，27（4）：10-16.

［8］HAJIAN M，RANJBAR A M，AMRAEE T，et al.Optimal placement of phasor measurement units：particle swarm optimi-zation approach［C］∥2007 International Conference on Intelligent Systems and Application to Power System.Toki Messe，Niigata，Japan：IEEE，2007：1-6.

［9］张作鹏，陈刚，白茂金.基于动态规划算法的 PMU 优化配置［J］.电网技术，2007，31（1）：51-56.ZHANG Zuopeng，CHEN Gang，BAI Maojin.PMU optimal placement based on dynamic programming ［J］.Power System Technology，2007，31（1）：51-56.

［10］罗毅，赵冬梅.电力系统PMU最优配置数字规划算法［J］.电力系统自动化，2006，30（9）：20-24.LUO Yi，ZHAO Dongmei.Optimal PMU placement in power system using numerical formulation ［J］.Automation of Electric Power Systems，2006，30（9）：20-24.

［11］SAJAN K S，TYAGIB.OptimalplacementofPMU with optimal branch current phasors for complete and incomplete observability［C］∥2011 IEEE Power and Energy Society General Meeting.San Diego，USA：IEEE，2011：1-5.

［12］沈天时，刘崇新，岳青，等.基于改进禁忌搜寻法的IEEE 30节点系统无功优化［J］.电工电气，2015（7）：19-23.SHEN Tianshi，LIU Chongxin，YUE Qing，et al.Reactive power optimization of IEEE 30 node system based on improved tabu search method［J］.Electrotechnics Electric，2015（7）：19-23.

［13］兰华，万旺经，王韵然，等.基于模拟退火混合遗传算法的电力系统相量测量装置优化配置［J］.电网技术，2007，31（2）：114-117.LAN Hua，WAN Wangjing，WANG Yunran，et al.An optimal PMUs placement in power systems based on the simulated annealing and genetic algorithm ［J］.Power System Technology，2007，31（2）：114-117.

［14］哈罗德.W.库恩.博弈论经典［M］.北京：中国人民大学出版社，2002：12-20.

［15］YE Jun，LIU Xiande，HAN Lu.Evolutionary game algorithm for continuous parameteroptimization ［J］.Information Processing Letters，2004，91（5）：211-219.

［16］徐敏.基于博弈思想的优化算法研究［D］.合肥：中国科技大学，2006.XU Min.Research on game theory idea based optimization algorithm ［D］.Hefei：University of Science and Technology of China，2006.

［17］堪忠瑞.多目标优化设计博弈分析方法的研究和应用［D］.杭州：浙江大学，2013.KAN Ruizhong.The research and application of multi-objective optimization design method based on game theory［D］.Hangzhou：Zhejiang University，2013.

［18］蔡田田，艾芊.电力系统中PMU最优配置的研究［J］.电网技术，2006，30（13）：32-37.CAI Tiantian，AI Qian.Research on optimal PMU placement in power systems［J］.Power System Technology，2006，30（13）：32-37.