Givens正交变换法状态估计中基于VPAIR消元的改进策略

刘 颖 ，童伟林 ，邹 宇 ，王建全，夏彦辉 ，肖谭南

（1.南京国电南自电网自动化有限公司，江苏 南京 211153；2.浙江大学 电气工程学院，浙江 杭州 310027）

0 引言

电力系统状态估计是能量管理系统（EMS）的重要组成部分，也是稳定控制、经济调度等其他电力系统应用的重要基础，在电网安全运行中承担着重要作用［1-2］。它利用实时测量系统的冗余度来提高数据精度，给出系统运行状态的估计值。

状态估计一般用非线性加权最小二乘法问题加以描述。正则方程法是早期状态估计的主要方法，包括加权最小二乘法、快速分解法等。但是，正则方程系数矩阵的条件数是量测雅可比矩阵条件数的平方，方程的病态性导致计算精度下降。在处理虚拟量测的情况下，方程病态问题更加突出。

对此，一类研究较多的方法是利用拉格朗日乘子法来处理等式约束［3］，但是该方法存在信息矩阵不正定和计算量大的不足。Cholesky分解法［4］能够提升算法的数值稳定性、克服信息矩阵不正定的情况，但计算效率仍然有待提高。使用修正牛顿法［5-7］处理等式约束计算简单，可以有效规避上述问题。

另一类研究方法则是利用正交变换法。正交变换法［8-9］是一种可以有效提高数值稳定性的计算方法，在电力系统状态估计中应用广泛。Givens旋转法及Household镜像法是正交变换的2种主要方法。Household镜像法适用于满矩阵的情况，而状态估计的加权雅可比矩阵一般比较稀疏，使用Givens正交变换法具有更高的效率。

在进行Givens正交变换过程中会产生大量的中间注入元素，增加了Givens旋转的次数和计算量，影响计算效率。选择合适的列编号顺序和消元策略，可以减少Givens正交变换的计算量。列编号顺序一般采用最小度原则，可以保证分解后矩阵的稀疏性。

而Givens正交变换的消元策略可分为逐行消元和逐列消元。早期的消元策略一般为逐行消元策略和定转轴逐列消元策略。而后续研究发现，变转轴逐列消元策略可以在很大程度上减少中间注入元素的数量，有效地改善算法的性能。文献［10］提出将最稀疏的一行作为固定转轴，其余行与转轴比较，按照注入元素的个数依次进行Givens旋转。文献［11］提出基于矩阵稀疏性的变转轴策略，选择最稀疏的2行进行Givens旋转。文献［12］提出基于最少注入元的VPAIR变转轴策略，选择产生中间注入元素最少的2行进行Givens旋转。文献［13］对几种策略进行了比较，证明采用最小度原则的列排序和VPAIR逐列变转轴策略是一种效率更高的方法。变转轴消元策略的正交变换法在状态估计中有广泛的应用［14-16］。

本文在VPAIR逐列变转轴策略的基础上，提出在其消元过程中动态调整量测排序的改进策略。与传统的策略相比，所提策略对量测排序进行了在线动态优化，可以进一步有效地减少注入元数量，提高计算效率。

1 正交变换法状态估计

状态估计用非线性加权最小二乘法问题描述如下：

其中，x为n维状态向量；z为m维量测向量；h（x）为m维量测方程向量；W为m×m阶量测权重矩阵（对角矩阵）。

对量测方程h（x）进行泰勒级数展开，取线性项，有：

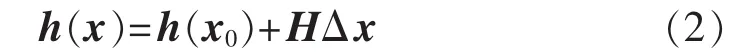
其中，H为量测雅可比矩阵。将式（2）代入式（1）可得到：

其中，r=z-h（x0）为 m 维量测残差向量；rw=W1/2r为m维加权量测残差向量；Hw=W1/2H为m×n阶加权量测雅可比矩阵；‖·‖2为欧几里得范数。

假设存在 m×m 阶正交矩阵 Q，使得式（4）、（5）成立，那么可得式（6）。

其中，R为n×n阶上三角矩阵；Z为（m-n）×n阶全零矩阵；b1为n维向量；b2为m-n维向量。

由于范数大于或等于 0，当式（7）成立时，J（Δx）达到最小值‖b2‖2。

因此，只需要构造矩阵Q就可以变换出R和b1，求解式（7）可以得到状态向量修正量Δx。矩阵Q可以通过对Hw的Givens变换或者Household变换获得。

2 Givens旋转

Givens正交变换过程中每次Givens旋转仅消去1个非零元素，直到对角线左边没有非零元素为止。以第i行和第j行2行元素为例说明。

当对第j行第k列以第i行第k列为转轴进行Givens旋转时，第i、j行第k列左边的元素均为0，以使第j行第k列的元素变为0。初始的第i、j行元素如下：

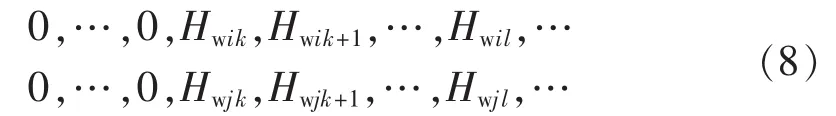
经过单次Givens变换，得到如下结果：

Givens变换推导后得到计算公式如下：

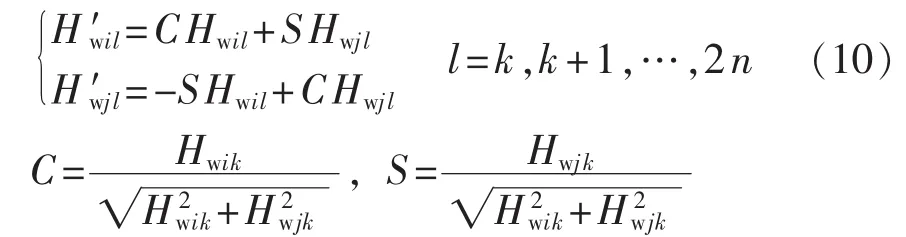
3 VPAIR消元策略

VPAIR消元策略是Robey提出的基于最少注入元的变转轴逐列消元策略，该策略经过大量算例验证，计算效率高，是目前被广泛采用的方法。其原则如下：

a.检查是否存在结构完全一致（无中间注入元）的2行，若有则直接进行Givens旋转；

b.计算所有旋转对产生的中间注入元个数，并对各旋转对产生注入元的个数进行比较，选择产生注入元个数最少的2行作为确定的旋转对进行Givens旋转；

c.在中间注入元个数一样的情况下，选择最稀疏的2行作为旋转对进行Givens旋转。

下面通过简单的4×3阶矩阵A来演示用VPAIR策略进行逐列变转轴Givens旋转的过程。原始矩阵A如式（11）所示。

其中，×表示非零元素。

步骤1：第1列共计有个旋转对可供旋转。旋转对［R3，R4］无注入元，故选之进行变换，元素（4，1）被消去，所得结果如式（12）所示。

其中，［Ri，Rj］表示第i行、第j行组成的旋转对；（i，j）表示矩阵第i行第j列元素。

步骤2：第1列有3个旋转对可供旋转，旋转对［R1，R2］和［R2，R3］均只有 1 个非零注入元，而旋转对［R1，R2］更稀疏，故选之。此时元素（2，1）被消去，同时产生注入元（1，1）（注入元用⊗表示），所得结果如式（13）所示。

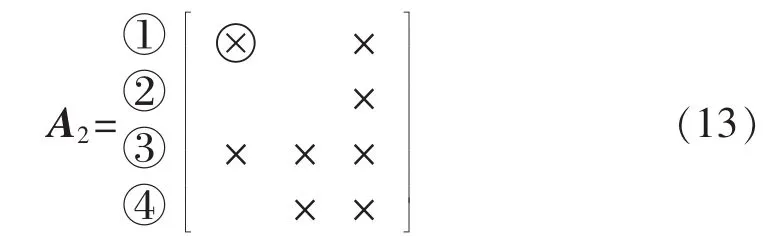
步骤 3：第1 列只剩下旋转对［R1，R3］，故选之进行变换。此时元素（3，1）被消去，同时产生注入元（1，2）。至此第1列旋转结束。所得结果如式（14）所示。

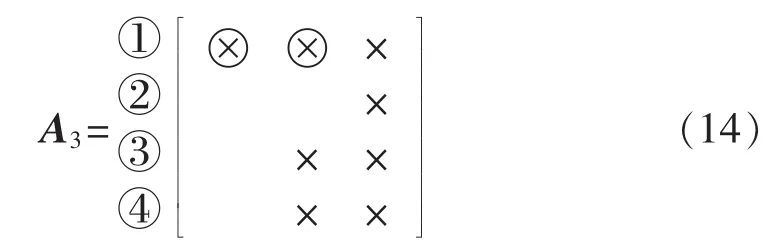
步骤 4：进行第2 列旋转。旋转对［R3，R4］无注入元，故直接选之进行变换，元素（4，3）被消去。所得结果如式（15）所示。

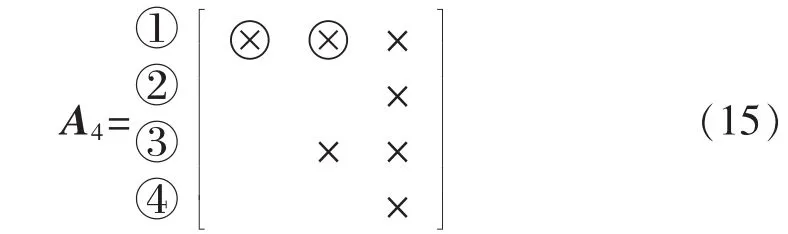
步骤 5：第2列只剩下旋转对［R2，R3］，故选之进行变换。元素（3，2）被消去，产生注入元（2，2）。至此第2列旋转结束。所得结果如式（16）所示。

步骤 6：第3列只剩下旋转对［R3，R4］，故选之进行变换。上三角矩阵R形成，旋转过程结束。所得结果如式（17）所示。

由上述可知，VPAIR策略为了实现严格的矩阵上三角结构，进行了6次旋转操作。

4 基于VPAIR消元的改进策略

4.1 改进策略的基本原理

VPAIR消元策略采用寻找产生最少注入元的旋转对进行变换，很大程度上减少了注入元的数量。但是，由4×3阶矩阵A不难发现，当对第i列进行旋转时，元素（i，i）出现了为0的情况。为了满足上三角矩阵R的结构特点，仍然要将该行纳入旋转对进行变换，这在一定程度上增加了注入元素的数量，降低了计算效率。由于电力系统状态估计的加权雅可比矩阵的大规模稀疏性，矩阵对角元素为0的情况更为普遍。对此，本文提出了基于VPAIR消元的改进策略。仍然采用逐列消元，具体步骤如下。

a.对第i列进行变换时，统计该列第i行以下（包括第i行）所有非零元素个数和非零元素所在行的信息。由非零元素所在行组成子矩阵。

b.对子矩阵进行VPAIR策略的消元，即寻找非零注入元个数最少的旋转对进行旋转。记录该列最后一次旋转的旋转轴所在行信息。

c.将该旋转轴所在行与第i行元素位置互换。d.进行第i+1列的变换。

上述策略的关键在于旋转过程中动态调整行排序（即量测排序），实现排序优化。由式（4）可知：

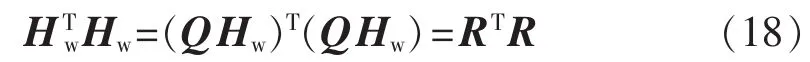
由式（18）可知，加权雅可比矩阵 Hw经Givens正交变换后得到的最终上三角矩阵R和信息矩阵平方根分解后得到的上三角矩阵相同。调整行排序的过程中虽然Hw发生变化，但是不会发生变化，所以最后的上三角矩阵R也是一致的。因此，改进策略不改变计算结果，从理论上而言是可行的。

4.2 改进策略的具体实现

为了说明改进策略的变换过程，同样采用上述4×3阶矩阵A进行演示。

步骤1：第1列有3个非零元素，共计个旋转对可供旋转。旋转对［R3，R4］无注入元，故选之进行变换，元素（4，1）被消去，所得结果如式（19）所示。

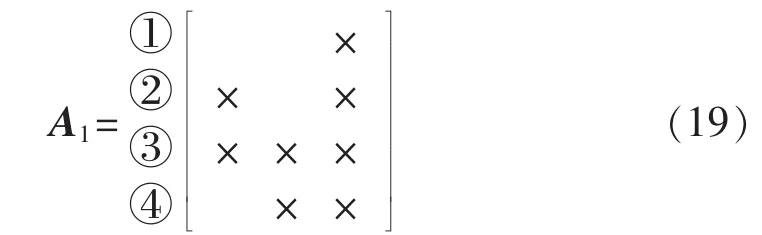
步骤2：A1第1列还有2个非零元素，组成唯一可供选择的旋转对［R2，R3］，故选之进行变换，元素（3，1）被消去。此时第1列只剩下第2行一个非零元素，该列旋转过程结束。将第2行元素与第1行元素位置互换，所得结果如式（20）所示。

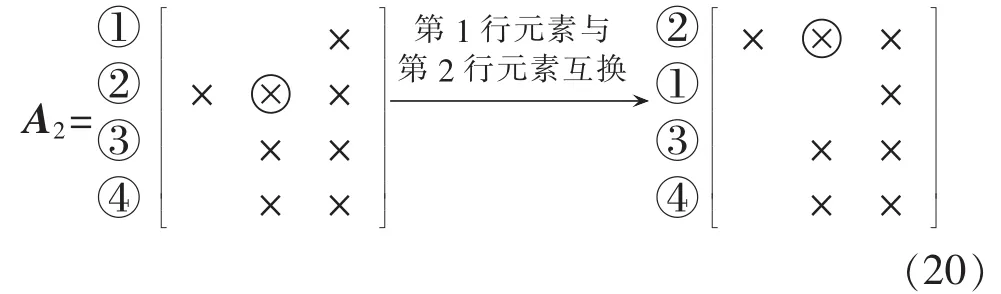
步骤3：第2列还有2个非零元素，组成唯一可供选择的旋转对［R3，R4］，选之进行变换，元素（4，1）被消去。此时第2列只剩下第3行一个非零元素，该列旋转过程结束。将第3行元素与第2行元素（如备注所示为原第1行）位置互换，所得结果如式（21）所示。

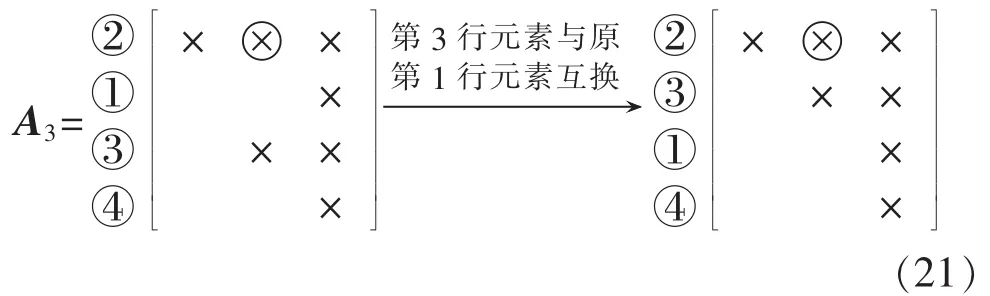
步骤 4：对第3 列唯一旋转对［R3，R4］（如备注所示为原［R1，R4］）进行变换，形成上三角矩阵 R（A4）。

通过演示可以发现对于4×3阶矩阵A而言，VPAIR策略需要进行6次旋转操作；改进策略进行了4次旋转操作和2次矩阵行位置互换操作。由第3节Givens旋转公式可知，每一次的旋转操作是复杂的，运行时间也远远大于位置互换操作的时间。因此，利用改进策略的Givens变换可以在很大程度上减少计算时间，提高计算效率。

由式（22）的结果不难发现，改进策略在得到最后上三角矩阵的同时，也给出了雅可比矩阵所在行（即量测量）的新排序。这种排序是在利用VPAIR策略进行Givens变换的过程中得到的更加优化的排序。该排序可以有效地规避旋转过程中处理对角元元素为0的情况，很大程度上提高了计算效率。

4.3 策略比较与分析

与一般加权最小二乘法处理对称矩阵不同，在正交变换法状态估计中，Givens旋转由于需要直接对加权雅可比矩阵进行处理，所以存在量测排序的优化问题。量测排序的合理与否，对旋转过程中产生注入元的数量会产生重要的影响。

VPAIR策略在选择最少注入元所在的行对进行变换的过程中，本质上也对量测排序进行了一定程度的优化。但是在逐列消元的过程中，该列最后一次Givens旋转的旋转轴所在行号与列号一致，是已经固定的。所以这种量测排序的优化只是半动态的优化策略，部分量测量顺序没有得到优化。

而改进策略在逐列消元过程中，避免了固定最后旋转轴所在行号的弊端，同时将最后的旋转轴所在行与和该列列号一致的行号进行在线动态的互换，调整了量测排序。这种量测排序的优化手段是一种动态的优化策略，因此具有更高的计算效率。

5 算例验证

为了验证所提改进策略的计算效率，并与VPAIR策略进行比较，2种策略均采用按照最小度原则的列排序，保证矩阵R稀疏性的同时，便于策略之间的比较。在IEEE 39、57、118节点系统和实际某区域23节点、区域433节点上分别进行了测试。选用主频为3.4 GHz、内存为8 G的台式机运行程序。测试算例的配置信息如表1所示。

表1 测试系统的配置信息Table 1 Configuration information of test systems

将原策略和改进策略分别在上述系统中进行运行和验证，计算结果如表2所示。其中旋转次数为状态估计中对加权雅可比矩阵Hw完成一次完整的正交变换，形成最终上三角矩阵R所进行的Givens旋转总次数，而CPU时间为完成上述正交变换的计算时间。

由表2可知，改进策略在Givens旋转总次数和计算时间上都有50%以上大幅度的减少。因此，改进策略的计算效率得到很大的提高。

表2 VPAIR策略与改进策略测试结果比较Table 2 Comparison of testing result between VPAIR strategy and improved strategy

6 结论

在电力系统状态估计中，针对正交变换法在变换过程中出现大量非零注入元的情况，本文在VPAIR变转轴逐列消元策略的基础上，提出消元过程中动态调整量测排序的改进策略。将所提改进策略与VPAIR策略在不同规模仿真系统运行比较，表明改进策略具有更高的计算效率，满足在线状态估计的要求。

本文提出的改进策略结合了量测排序的动态优化，简单有效，切实可行，能够有效提高计算效率。

参考文献：

［1］林伟芳，汤涌，孙华东，等.巴西“2·4”大停电事故及对电网安全稳定运行的启示［J］.电力系统自动化，2011，35（9）：1-5.LIN Weifang，TANG Yong，SUN Huadong，etal.Blackoutin Brazilpowergrid on February 4，2011 and inspirationsfor stable operation of power grid［J］.Automation of Electric Power Systems，2011，35（9）：1-5.

［2］钟庆，张哲，许中，等.广州配电网故障停电事故的自组织临界特征［J］.电力自动化设备，2017，37（4）：109-113.ZHONG Qing，ZHANG Zhe，XU Zhong，et al.SOC characteristics of power-supply failure of Guangzhou distribution network［J］.Electric Power Automation Equipment，2017，37（4）：109-113.

［3］倪小平，张步涵.一种带有等式约束的状态估计新算法［J］.电力系统自动化，2001，25（21）：42-44.NIXiaoping，ZHANG Buhan.New stateestimation algorithm with equality constraints［J］.Automation of Electric Power Systems，2001，25（21）：42-44.

［4］KORRES G N.A robustalgorithm forpowersystem state estimation with equality constraints［J］.IEEE Transactions on Power Systems，2010，25（3）：1531-1541.

［5］郭烨，张伯明，吴文传，等.直角坐标下含零注入约束的电力系统状态估计修正牛顿法［J］.中国电机工程学报，2012，32（19）：96-100.GUO Ye，ZHANG Boming，WU Wenchuan，et al.Power system state estimation solution with zero injection constraints using modified Newton method［J］.Proceedings of the CSEE，2012，32（19）：96-100.

［6］郭烨，张伯明，吴文传，等.极坐标下含零注入约束的电力系统状态估计的修正牛顿法与快速解耦估计［J］.中国电机工程学报，2012，32（19）：113-117.GUO Ye，ZHANG Boming，WU Wenchuan，et al.Power system state estimation solution with zero injection constraints using modified Newton method and fast decoupled method in polar coordinate［J］.Proceedings of the CSEE，2012，32（19）：113-117.

［7］常鲜戎，樊瑞.计及零注入节点约束的混合量测分区状态估计方法［J］.电网技术，2015，39（8）：2254-2257.CHANG Xianrong，FAN Rui.A mixedmeasurementpartition state estimation method taking zero injection node constraint into account［J］.Power System Technology，2015，39 （8）：2254-2257.

［8］刘广一，胡锡龙，于尔铿，等.快速正交变换阻尼最小二乘法在电力系统状态估计中的应用［J］.中国电机工程学报，1991，11（6）：34-40.LIU Guangyi，HU Xilong，YU Erkeng，et al.Application of fast orthogonal transformation with damping factor to power system state estimation［J］.Proceedings of the CSEE，1991，11（6）：34-40.

［9］VEMPATI N，SLUTSKER I W，TINNEY W F.Orthogonal sparse vector methods［J］.IEEE Transactions on Power Systems，1992，7（2）：926-932.

［10］DUFF I S.Pivot selection and row ordering in Givens reduction on sparse matrices［J］.Computing，1974，13（3-4）：239-248.

［11］GENTLEMAN W M.Row elimination for solving sparse linear systems and least squares problems［J］.Springer Berlin Heidelberg，1976，506：122-133.

［12］ROBEY T H，SULSKY D L.Row ordering for a sparse QR decomposition［J］.SIAM Journal of Matrix Analysis and Applications，1994，15（4）：1208-1225.

［13］PANDIAN A，PARTHASARATHY K，SOMAN S A.Towards fast givens rotations based power system state estimator［J］.IEEE Transactions on Power Systems，1999，14（3）：837-843.

［14］杜正春，牛振勇，方万良.基于分块QR分解的一种状态估计算法［J］.中国电机工程学报，2003，23（8）：50-55.DU Zhengchun，NIU Zhenyong，FANG Wanliang.A block QR based power system state estimation algorithm［J］.Proceedings of the CSEE，2003，23（8）：50-55.

［15］郭瑞鹏，邵学俭，韩祯祥.基于分块吉文斯旋转的电力系统状态估计［J］.中国电机工程学报，2006，26（12）：26-31.GUO Ruipeng，SHAO Xuejian，HAN Zhenxiang. A blocked givens rotations based algorithm for power system state estimation［J］.Proceedings of the CSEE，2006，26（12）：26-31.

［16］WANG G，ALI K，XU J.An efficient engine for orthogonal SE［C］∥Proceedingsofthe Third InternationalConference on Control Automation&Systems Engineering.［S.l.］：CASE，2013：13-17.