直流系统无功动态特性及其对受端电网暂态电压稳定的影响
杨欢欢,蔡泽祥 ,朱 林 ,冯 雷 ,金小明 ,周保荣 ,张东辉
(1.华南理工大学 电力学院,广东 广州 510640;2.南方电网科学研究院,广东 广州 510080)
0 引言
直流输电系统在大规模远距离输电中的广泛应用使得其在系统中所占的比例越来越高,受端电网中的直流落点也越来越密集,交流系统发生故障可能导致多回直流系统同时换相失败,从而使有功和无功功率产生较大的扰动,恶化受端电网的暂态电压稳定,威胁交直流系统的安全稳定运行[1-2]。
引起暂态电压不稳定的根本原因是电力系统的无功电源和无功负荷的动态失衡[3],受端电网电压支撑强度、电动机负荷、直流系统、网络结构是暂态电压稳定的主要影响因素。交流系统发生故障后,直流换流器从受端电网吸收大量无功是直流系统影响暂态电压稳定的主要原因[4-6]。文献[7-9]分析了直流控制与直流系统无功动态特性的关系,并从优化直流控制的角度,降低大扰动后的直流系统无功,从而减小直流系统对受端电网暂态电压稳定的影响,但对直流系统对受端电网暂态电压稳定的影响机理认识不足。文献[10-11]通过衡量交流系统对直流系统的电压支撑强度,提出了短路比(SCR)、多馈入短路比(MISCR)等指标,用于分析直流系统对受端电网暂态电压稳定的影响,认为SCR或MISCR越大,直流系统对受端电网暂态电压稳定的影响越小。但SCR系列指标仅体现了交流系统对直流系统的电压支撑强度[12],用其来评价直流系统对受端电网暂态电压稳定的影响存在固有的缺陷。临界切除时间能准确地评价直流系统对受端电网暂态电压稳定的影响[13-14],但其严重依赖于数值仿真,难以建立完备的分析方法和评价体系。因此,亟需研究直流系统对受端电网暂态电压稳定影响的评估方法及指标以指导直流系统的规划和运行。
本文在对大扰动后直流系统无功动态特性进行深入研究的基础上,提出了直流系统受扰后无功源-荷转换的新观点。结合暂态电压失稳的物理本质,揭示了直流系统无功源-荷转换特性对受端电网暂态电压稳定的影响机理和途径,并根据临界暂态电压稳定时直流系统无功的变化规律,提出了一种直流系统无功动态特性的定量刻画方法。在此基础上,构建了综合考虑直流系统无功动态特性、无功网络传递特性和直流落点电压支撑强度的评价直流系统对受端电网暂态电压稳定影响的指标。以南方电网为背景,利用所提指标评估了不同直流输电系统对受端电网暂态电压稳定的影响,相关结果与采用临界切除时间变化量指标所得到的结果具有一致性,从而验证了所提指标的有效性和实用性。
1 大扰动下直流系统无功动态特性分析
以换流母线为界,交直流系统分为交流系统部分和直流系统部分,如图1所示。图中,Uac为换流母线电压;Ud和Id分别为直流电压和电流;Pd为直流系统有功功率;Qd为换流器(包括换流变)消耗的无功功率,简称换流器无功;Qc为滤波器的无功功率,简称补偿无功,B为其等效电纳;Qa为直流系统从交流系统吸收的无功功率,简称直流系统无功。

图1 交直流系统示意图Fig.1 Schematic diagram of AC/DC system
Qa可由式(1)表示。

其中,k为换流变变比;N为每极桥数;Xc为等效换相电抗;φ为功率因数角;γ为熄弧角;α为触发角。
稳态运行时,直流系统从交流系统吸收的无功基本为0。当交流系统遭受较大扰动而导致换流母线电压变化时,在毫秒级的时间框架内,直流电压、直流电流和熄弧角都将随之变化,从而导致换流器无功随之变化。而秒级时间框架内的机械投切并联补偿装置动作时间相对较长(直流系统无功越限后5 s投入或10 s退出),补偿无功无法实时跟踪换流器无功,从而导致逆变站的无功就地平衡状态被破坏,直流系统多余或缺少的无功将由与之相连的交流系统吸收或提供。
图2为云广特高压直流输电系统受端电网发生三相金属性对称故障且导致换流母线电压跌至0.6 p.u.时,熄弧角、直流电流、换流器无功、补偿无功以及直流系统无功的变化曲线。
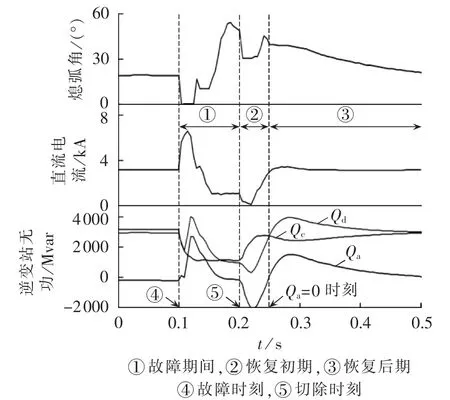
图2 直流系统无功动态特性Fig.2 Dynamic characteristic of HVDC reactive power
由图2可知,大扰动后的直流系统无功动态特性可划分为如下3个阶段。
a.故障期间,换流母线电压降低,补偿无功、直流系统无功均减小;由于直流系统换相失败,直流电流增大,直流系统无功随之有所增大;随着低压限流环节(VDCOL)的动作(故障后 20 ms),直流电流迅速减小,直流系统无功也随之减小,但其仍大于补偿无功,因此直流系统将从交流系统吸收无功。
b.恢复初期,补偿无功随着换流母线电压的恢复而恢复,但直流电流由于VDCOL的延时作用(达到门槛电压后75 ms退出),恢复有所延迟,从而导致换流器无功无法在故障切除后立即开始恢复,此时的补偿无功大于换流器无功,直流系统将向交流系统注入无功。
c.恢复后期,换流器无功随直流电流的恢复而逐渐增大,在换流器无功峰值附近,直流电压和电流基本恢复到额定值,但由于熄弧角超调,换流器无功持续大于补偿无功,直流系统在很长的一段时间需要从交流系统吸收大量的无功。
2 直流系统无功动态特性对暂态电压稳定的影响分析
2.1 暂态电压稳定和感应电动机稳定的一致性分析
感应电动机无功电压特性是交流电网暂态电压稳定最重要的影响因素。故障期间滑差越过不稳定平衡点的感应电动机在故障切除后将趋于堵转并吸收大量的无功,拖累附近的电压下降,并导致临近的其他感应电动机堵转,从而产生区域性的感应电动机群无功需求激增的效应,导致系统无功动态不平衡进一步恶化,系统电压进一步下降,最终演变成全网的暂态电压稳定问题。因此,暂态电压稳定常常也被称为负荷稳定[16]。
本文关注直流系统无功动态特性对直流落点受端超高压电网暂态电压稳定的影响。一方面,低压电网一台或几台小容量感应电动机的堵转并不意味着高压电网的暂态电压失稳;另一方面,当将低压母线的电动机等值到所关注电压等级(如500 kV)的高压母线时,等值感应电动机的无功电压特性实际上代表了该区域的低压感应电动机的集群效应。此时,该等值感应电动机的失稳堵转就与相应500 kV母线的暂态电压失稳一致。实际上,目前关于大电网暂态电压稳定的数值仿真也做不到对全网低电压小容量感应电动机的全建模,而是采用考虑500 kV高压母线出线的综合负荷模型。因此,本文在评估直流系统对直流落点电网暂态电压稳定影响时,采用相应500 kV母线的等值感应电动机的稳定性来表征相应母线的暂态电压稳定性是合理的。
图3为云广直流逆变侧换流母线发生同一类型但不同故障持续时间的三相短路故障时,等值感应电动机负荷的滑差和500 kV母线电压的仿真曲线(滑差、电压为标幺值),不同的故障持续时间分别对应等值感应电动机和母线暂态电压的稳定、临界稳定、临界不稳定和不稳定4种场景。由图3可以看出,4种场景下等值感应电动机的稳定性与相应母线的暂态电压稳定性是一致的。
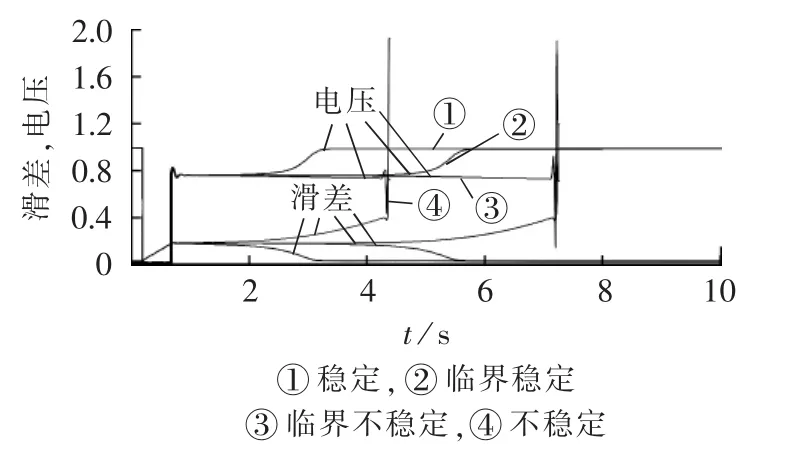
图3 等值感应电动机负荷滑差和母线电压曲线Fig.3 Load slip and bus voltage curves of equivalent induction motor
2.2 直流接入后对暂态电压稳定的影响
由直流系统无功动态特性的分析结果知,对受端电网而言,大扰动后直流系统无功的性质在无功电源、无功负荷间不断变化,呈现无功源-荷转换特性,从而构成了影响受端电网暂态电压稳定的新因素。
图4为在分别考虑直流和不考虑直流的场景下,云广特高压直流输电系统受端电网发生三相短路且临界暂态电压稳定时电动机无功和直流系统无功的变化曲线。由图4可知,直流系统的接入使故障的临界切除时间减小,受端电网的暂态电压稳定性降低,即恶化了暂态电压稳定性。

图4 临界暂态电压稳定时电动机负荷和直流系统的无功Fig.4 Reactive power of induction motor load and HVDC with stable critical transient voltage
由于不同阶段直流系统的无功性质不同,其对暂态电稳定的影响也不同:故障期间,直流系统从交流系统吸收无功,进一步降低了系统的电压水平,但此时电动机负荷的无功需求较小,直流系统对受端电网暂态电压稳定的影响较小;恢复初期,直流系统向交流系统输送无功,有利于系统的电压恢复,但该过程持续时间较短,直流系统对受端电网暂态电压稳定的影响也较小;恢复后期,直流系统从交流系统吸收大量的无功,正好与电动机增大的无功需求相叠加,恶化了受端电网的无功动态平衡,降低了受端电网的暂态电压稳定性。
综上可知,大扰动后直流系统无功源-荷转换特性中对受端电网暂态电压稳定影响最大的是恢复后期的无功负荷特性。
3 直流系统无功动态特性的解析刻画
3.1 直流系统无功峰值的时间特性分析
图5为不同故障持续时间下的直流系统无功变化情况。图中,Qam为直流系统无功峰值,tm为其对应时刻;tc为故障切除时刻;Δtcm为故障切除时刻到无功峰值时刻的时间间隔。
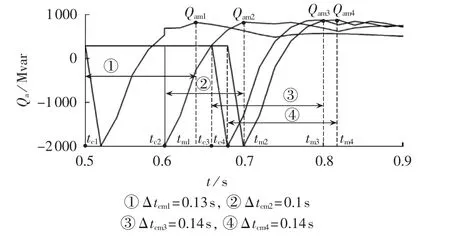
图5 不同故障持续时间下的直流系统无功动态特性Fig.5 Dynamic characteristic of HVDC reactive power with different failure duration
由图5可知,不同故障持续时间下的直流系统无功基本都在故障切除后0.1 s达到峰值,且峰值大小基本相同。随着故障持续时间增大,恢复后期的直流系统无功维持在峰值附近的时长也增大。当故障持续时间等于系统临界切除时间时,恢复后期的直流系统无功大小将长时间维持在峰值附近。对受端电网而言,此时直流系统相当于无功负荷,无功虽略有增加,但变化不大,可将其等效为恒无功负荷。
3.2 直流系统无功峰值解析求解
在以上分析的基础上,本文试图采用解析的方式求解恢复后期直流系统的无功峰值,从而避免直流系统无功动态特性的刻画依赖于仿真。由式(1)可知,求解直流系统无功峰值需已知换流母线电压、直流电流、触发角和熄弧角这4个变量。
a.直流控制对直流系统无功峰值的影响。
大扰动后直流系统的无功动态特性主要取决于极控层,其控制功能主要由定电流控制、定电压控制和定熄弧角控制3个控制环节协调配合完成,如图6所示。图中,Udact、Idact和 γact分别为实际直流电压、电流和熄弧角;Udref、Idref和 γref分别为直流电压、电流和熄弧角参考值;Idmarg为直流电流裕度。
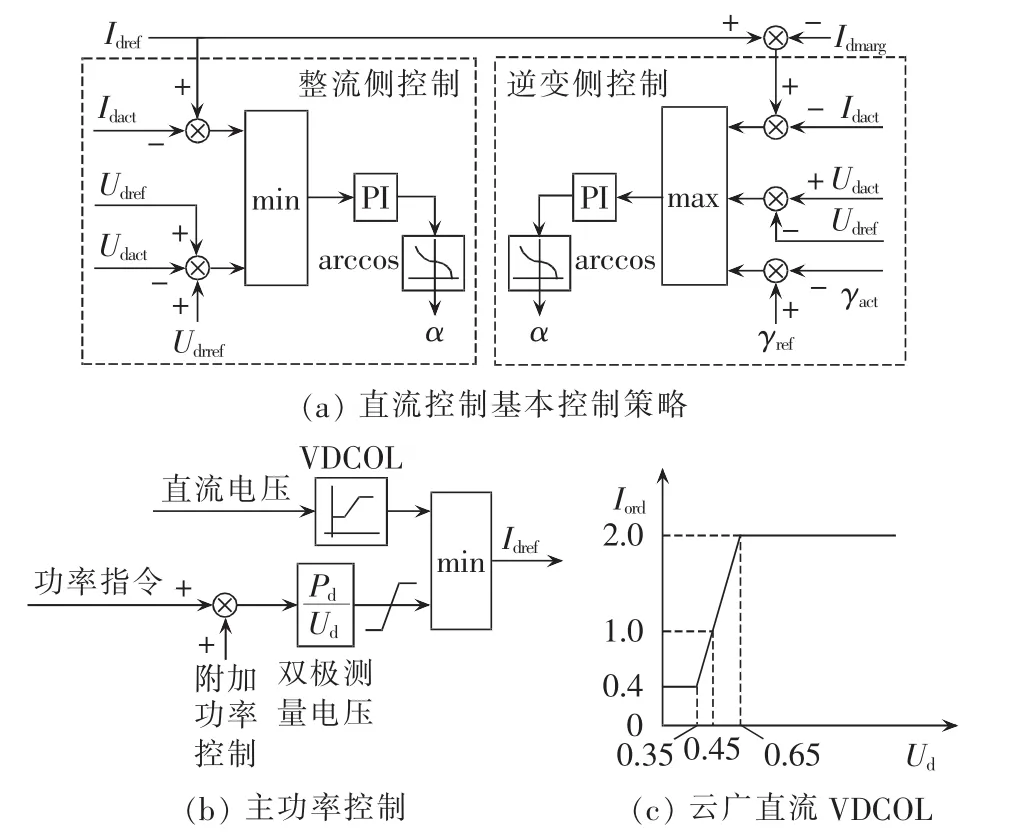
图6 直流系统的主控制和极控制Fig.6 Master control and pole control of HVDC
稳态运行时,整流侧运行在定电流控制方式,主功率控制为定电流控制提供参考值以使直流系统保持为恒功率运行。当直流电压由于交流系统发生故障而降低时,直流控制将通过VDCOL降低直流电流参考值,从而降低直流电流和功率。整流侧也配置有VDCOL以防止过电压,但其仅作为限制器使用。
逆变侧在稳态情况下运行在定电压控制方式,当换流母线电压降低时运行在定熄弧角控制方式,以保证换相裕度,定电流控制只在整流侧交流电压大幅下降且无法维持直流电流恒定时才起作用。
由此可知,在恢复后期,由于交流系统电压水平尚未完全恢复,换流母线电压将低于故障前水平,直流系统的整流侧将继续运行在定电流控制方式,逆变侧将由定电压控制方式切换到定熄弧角控制方式。而直流电压随着换流母线电压的恢复而有所恢复,所以VDCOL在恢复后期将退出运行(退出门槛电压为 0.45 p.u.)。
图7为云广特高压直流输电系统受端电网发生三相短路且临界暂态电压稳定时,换流母线电压(标幺值)、直流电流、触发角和熄弧角的变化曲线。
由图7可知,换流母线电压在恢复后期基本维持在相对较为稳定的值,在该过程中毫秒级响应的直流控制有充足的调节时间,直流电流在整流侧定电流控制作用下基本可恢复到扰动前的大小,熄弧角在逆变侧定熄弧角控制作用下也基本可恢复到扰动前的大小。因此,求解恢复后期的直流系统无功峰值仅需知道换流母线电压和触发角这2个变量。
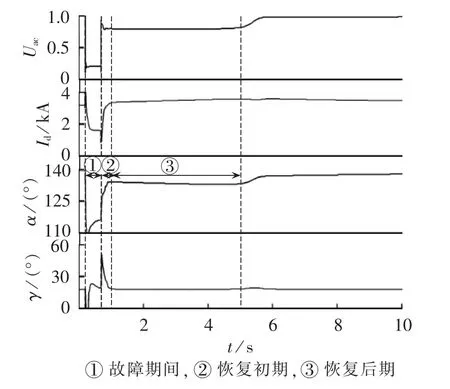
图7 临界暂态电压稳定时的Uac、Id、α和γFig.7 Curves of Uac,Id,α and γ with stable critical transient voltage
根据式(1)可得直流电压Ud为:

其中,γ0和Id0分别为扰动前的熄弧角和直流电流。
Ud也可以由式(3)求得:

由式(2)和式(3)可得触发角 α:

由式(4)可知,在直流电流、熄弧角的大小恢复到扰动前大小的情况下,临界暂态电压稳定时恢复后期的换流母线电压是求解直流系统无功峰值的关键。
b.换流母线电压的求解。
图8为含有多直流接入的交直流系统示意图。图中,点j为所考察的直流系统的接入点,也是扰动点;Uacj为换流母线电压;点i为点j扰动所导致的失稳电动机节点;Uaci为机端母线电压;Qamj为恢复后期点j的直流系统无功峰值。

图8 含多直流系统接入的交直流系统Fig.8 AC/DC system with multi-infeed HVDC
当换流母线点j遭受扰动而导致点i的电动机失稳时,电动机滑差将不断增大并最终堵转(滑差等于1 p.u.),机端电压也将随着滑差的增大而降低且扰动清除后无法恢复,即系统暂态电压失稳。
失稳节点i处的电动机堵转时,其等值阻抗不再变化,相当于恒阻抗负荷。忽略电动机的定子电阻、励磁电抗,可得堵转电动机的简化等值电路,见图9。图中,XTHi、ETHi分别为电动机机端的戴维南等值电抗、电势;X为电动机的定子电抗、转子电抗之和;R为电动机的定子电阻、转子电阻之和。
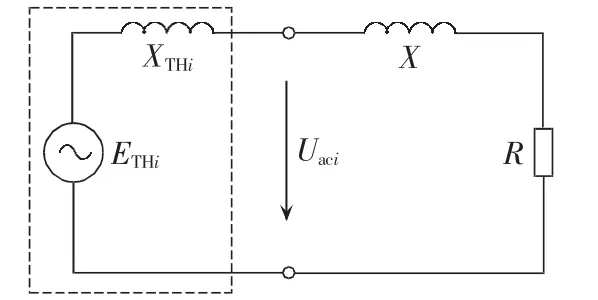
图9 堵转电动机的简化等值电路Fig.9 Simplified equivalent circuit of locked motor
可求得节点i失稳电动机的基准功率SMi为:

其中,Ppf为潮流中节点i的有功负荷;Ker为节点i的电动机负荷比例;KL为负载率。
将XTHi折算到感应电动机侧,可得:

其中,Saci为节点i失稳电动机机端的运行短路容量。
所以节点i失稳电动机的机端电压Uaci为:

由于暂态电压失稳一般是局部的,直流换流母线发生故障对其电气距离最近的电动机负荷影响最大。出于经济性的考虑,直流系统往往直接落点于负荷中心,所以直流接入点j(也是扰动点)和暂态电压失稳节点i的电气距离一般较近,因此可以近似认为Uacj=Uaci。
c.直流系统无功峰值的解析计算。
结合式(1)、(4)—(7)可求得恢复后期节点 j的直流系统无功峰值Qamj,如式(8)所示。

4 直流系统无功动态特性对暂态电压稳定影响的评价指标
在受端电网故障恢复期间,直流系统的接入会使节点j的无功需求增加Qamj,由此所导致的直流接入点j的电压变化ΔUj为:

其中,Sacj为直流接入点j的短路容量。
暂态电压失稳节点i的电压由于直流接入点j的电压变化ΔUj而产生的变化ΔUij为:
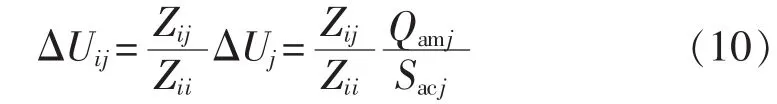
其中,Zii为暂态电压失稳节点i的自阻抗;Zij为暂态电压失稳节点i与直流接入点j之间的互阻抗。
ΔUij反映了节点j接入的直流系统对失稳节点i的电压水平的影响程度,ΔUij越大表明节点j的直流系统变化对失稳节点i电压的影响越大,即对受端电网暂态电压稳定性的影响越大。因此,可以构建如式(11)所示的直流系统对受端电网暂态电压稳定影响的评价指标 DCII(HVDC Influence Index)。

其中,MIIFij为暂态电压失稳节点i和直流接入点j之间的相互作用因子,其大小为节点i和j之间的互阻抗与节点i的自阻抗的比值的绝对值,即MIIFij=。
DCII综合考虑了直流系统的无功扰动大小、无功在网络中的传递和直流落点的电压支撑强度。因此,DCII可以用来评价直流系统的容量和落点的选择、受端电网动态无功支撑选址方案等工作,对于交直流电力系统的规划运行具有重要的指导意义。
5 算例
5.1 指标的验证与分析
以南方电网2015年丰大方式为例,2015年落点至受端广东电网的直流回路数达到8回,分别为高肇直流、溪洛渡直流(同塔双回)、云广直流、天广直流、糯扎渡直流、兴安直流、三广直流。为了排除功角稳定的影响,在保证发电机出口侧短路电流不变的前提下,发电机全部采用暂态电抗后电势不变的模型。负荷全部等值到500 kV母线(北郊站等值到200 kV母线),由60%感应电动机负荷+40%恒阻抗负荷组成,电动机参数参见文献[14]。
以逆变侧换流母线发生三相金属性故障为例,各直流逆变侧换流母线的短路容量Sac、临界暂态电压稳定时的直流系统无功峰值Qam、直流接入点与暂态电压失稳点间的相互作用因子以及根据式(11)求得的DCII如表1所示。
考虑直流系统时受端电网发生三相短路故障下临界切除时间为tc0,不考虑直流系统时的临界切除时间为tc1,Δt表示两者的相对变化率,即:
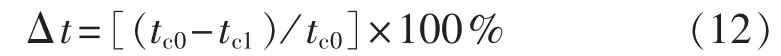
临界故障切除时间反映了系统的暂态电压稳定性,直流系统接入之后临界切除时间的相对变化率Δt反映了直流系统对暂态电压稳定性的影响[13-14]。Δt越大,表示直流系统对受端电网暂态电压稳定的影响越大;反之,则越小。本文采用Δt指标和DCII评估各直流系统对受端电网暂态电压稳定的影响,以验证DCII的有效性。
各直流逆变侧换流母线发生三相金属性故障情况下的tc0和tc1以及Δt如表2所示。
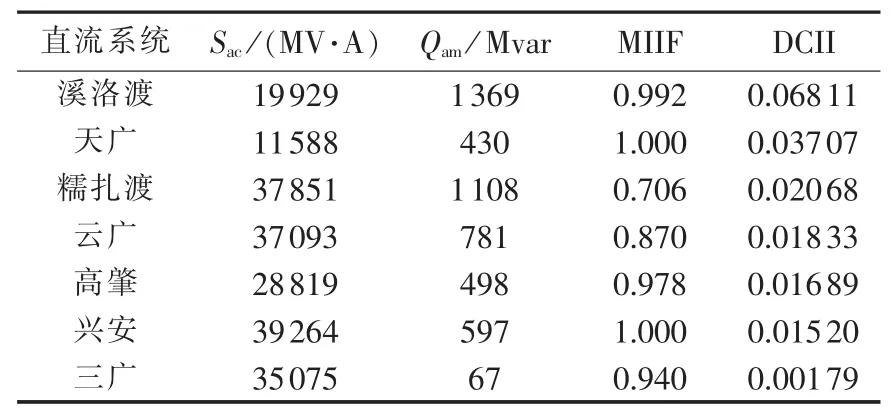
表1 Sac、Qam、MIIF 和 DCII值Table 1 Values of Sac,Qam,MIIF and DCII

表2 临界切除时间Table 2 Critical clearing time
由表1可知,根据本文提出的DCII,直流系统对广东电网暂态电压稳定影响大小的排序为:溪洛渡>天广>糯扎渡>云广>高肇>兴安>三广。对比表2可知,该排序与根据Δt的排序完全一致,说明DCII准确地反映了直流系统对受端电网暂态电压稳定的影响,从而验证了DCII的有效性和实用性。
5.2 与SCR指标的比较
SCR指标是目前常用的衡量交流系统和单直流系统相对强弱的指标,SCR越大,受端电网对直流系统的电压支撑能力越强,即直流系统对受端电网暂态电压稳定的影响越小。在SCR的基础上,CIGRE(International Council on Large Electric systems)工作组又提出了MISCR指标,与SCR相比,MISCR考虑了直流间的相互影响。
各直流系统逆变侧的SCR和MISCR见表3。
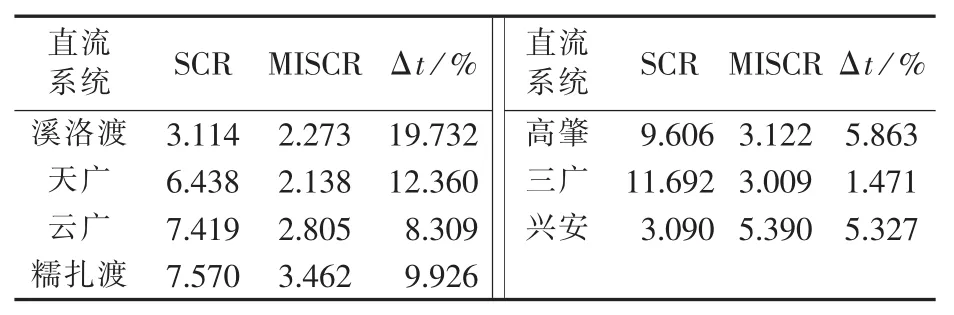
表3 各直流系统逆变侧SCR、MISCR和相对变化率Table 3 SCR,MISCR and relative change rate of inverter side of HVDC
由表3可知,根据SCR指标,直流系统对广东电网暂态电压稳定影响大小的排序为溪洛渡>天广>云广>糯扎渡>高肇>三广>兴安;根据MISCR指标,直流系统对广东电网暂态电压稳定影响大小的排序为天广>溪洛渡>云广>三广>高肇>糯扎渡>兴安。该排序与Δt指标排序的一致性较差,说明SCR或MISCR指标不能准确地反映直流系统对受端电网暂态电压稳定的影响。对比SCR(或MISCR)和DCII可知,SCR(或MISCR)仅反映了节点的电压支撑强度Sac和直流系统有功静态特性Pd;而DCII综合考虑了直流系统无功动态特性Qam、无功网络传递特性MIIF和直流落点的电压支撑强度Sac,更体现了直流系统对受端电网暂态电压稳定影响的本质。
6 结论
a.大扰动后的直流系统无功功率存在源-荷转换的特性,恶化了受端电网的无功动态平衡,构成了影响受端电网暂态电压稳定的新因素。
b.直流系统无功源-荷转换的特性中,对受端电网暂态电压稳定影响最大的是恢复后期的无功负荷特性,当交直流系统临界暂态电压稳定时,恢复后期的直流系统无功基本恒定不变。在此基础上,提出了定量刻画恢复后期直流系统无功峰值的解析求解方法,使得直流系统无功的获得不用依赖于仿真。
c.提出了综合考虑直流系统无功动态特性、无功网络传递特性和直流落点电压支撑强度的评价直流系统对受端电网暂态电压稳定影响的DCII,与传统的SCR系列指标相比,DCII更能体现直流系统对受端电网暂态电压稳定影响的本质,相关仿真结果验证了DCII的有效性和实用性。
参考文献:
[1]王永平,赵文强,杨建明,等.混合直流输电技术及发展分析[J].电力系统自动化,2017,41(7):156-167.WANG Yongping,ZHAO Wenqiang,YANG Jianming,et al.Hybrid high-voltage direct current transmission technology and its development analysis[J].Automation of Electric Power Systems,2017,41(7):156-167.
[2]李妮,李兴源,冯明,等.改善多馈入直流系统电压无功特性的直流控制策略[J].电力自动化设备,2016,36(2):25-31.LI Ni,LI Xingyuan,FENG Ming,et al.DC control for improving voltage and reactive power characteristics of multi-infeed HVDC system [J].Electric Power Automation Equipment,2016,36(2):25-31.
[3]KUNDUR P.Power system stability and control[M].New York,USA:McGraw-Hill,1994:27.
[4]蔡泽祥,冯雷,杨欢欢,等.高压直流系统无功动态对暂态电压稳定的影响[J].华南理工大学学报(自然科学版),2017,45(4):1-7.CAI Zexiang,FENG Lei,YANG Huanhuan,et al.Influence of reactive power dynamics of HVDC system on short-term voltage stability[J].Journal of South China University of Technology(Natural Science Edition),2017,45(4):1-7.
[5]AIK D L H,ANDERSSON G.Analysis of voltage and power interactions in multi-infeed HVDC systems[J].IEEE Transactions on Power Delivery,2013,28(2):816-824.
[6]欧开健,荆勇,任震.多馈入直流输电系统换流母线电压稳定性评估模型和算法[J].电力自动化设备,2003,23(9):23-26.OU Kaijian,JING Yong,REN Zhen.Model and algorithm for assessing voltage stability at commutation buses in MIDC system[J].Electric Power Automation Equipment,2003,23(9):23-26.
[7]杨欢欢,朱林,蔡泽祥,等.直流控制对直流系统无功动态特性的影响分析[J].电网技术,2014,38(10):2631-2637.YANG Huanhuan,ZHU Lin,CAIZexiang,etal.Influenceof HVDC control on HVDC reactive power dynamic characteristic[J].Power System Technology,2014,38(10):2631-2637.
[8]刘晓明,慈文斌,刘玉田.直流控制方式对受端电网电压稳定性影响[J].电力自动化设备,2011,31(4):69-73.LIU Xiaoming,CI Wenbin,LIU Yutian.Influence of DC system control mode on voltage stability of receiving-end power grid[J].Electric Power Automation Equipment,2011,31(4):69-73.
[9]刘崇茹,张伯明.直流输电系统控制参数对交直流连接母线电压幅值的影响[J].电力自动化设备,2007,27(5):23-27.LIU Chongru,ZHANG Boming.Influence of DC control parameters on joint buses of AC /DC hybrid power systems[J].Electric Power Automation Equipment,2007,27(5):23-27.
[10]郭小江,郭剑波,马世英,等.基于多馈入短路比的多直流落点选择方法[J].中国电机工程学报,2013,33(10):36-42.GUO Xiaojiang,GUO Jianbo,MA Shiying,et al.A method for multiDC terminallocation selection based on multi-infeed short circuit ratio[J].Proceedings of the CSEE,2013,33(10):36-42.
[11]金小明,周保荣,管霖,等.多馈入直流交互影响强度的评估指标[J].电力系统自动化,2009,33(15):98-102.JIN Xiaoming,ZHOU Baorong,GUAN Lin,et al.HVDC interaction strength index for the multi-infeed HVDC power system[J].Automation of Electric Power Systems,2009,33(15):98-102.
[12]黄弘扬,徐政,许烽.多馈入直流输电系统短路比指标的有效性分析[J].电力自动化设备,2012,32(11):46-50.HUANG Hongyang,XU Zheng,XU Feng.Effectiveness of short circuit ratio index for multi-infeed HVDC system[J].Electric Power Automation Equipment,2012,32(11):46-50.
[13]袁志昌,刘文华,宋强.基于暂态电压稳定指标的动态无功优化配置方法[J].电力系统自动化,2009,33(14):17-21.YUAN Zhichang,LIU Wenhua,SONG Qiang.Optimal allocation method of dynamic var compensation based on transient voltage stability index[J].Automation of Electric Power Systems,2009,33(14):17-21.
[14]孙华东,周孝信,李若梅.感应电动机负荷参数对电力系统暂态电压稳定性的影响[J].电网技术,2005,29(23):1-6.SUN Huadong,ZHOU Xiaoxin,LI Ruomei.Influence of induction motor load parameters on power system transient voltage stability[J].Power System Technology,2005,29(23):1-6.
[15]DIAZ D L J A,TAYLOR C W.Understanding and solving short-term voltage stability problems[C]∥PowerEngineering Society Summer Meeting.Chicago,IL,USA:IEEE,2002:745-752.

