基于切片反射采样的风电并网系统可用输电能力概率风险评估

张晓英 ，贾 磊 ，王 琨 ，张蜡宝 ，陈 伟

（1.兰州理工大学 电气工程与信息工程学院，甘肃 兰州 730050；2.国网甘肃省电力公司电力科学研究院，甘肃 兰州 730030；3.南京大学 电子科学与工程学院，江苏 南京 210093）

0 引言

“十三五”期间，国家电网正在进一步增加可再生能源（风能、太阳能、潮汐能等）在电力系统中的比例，尽管这些能源资源丰富、无污染、可再生，但要将这些新能源并入电网中却存在很多挑战［1］。特别是风电，其发电状况受气候与天气影响较大，在一天内可能波动幅度巨大，不稳定性与不可靠性是造成其无法大规模消纳的重要因素。因此，在满足各区域用电的前提下，有效评估可用输电能力ATC（Available Transfer Capability）［2］可以为风电基地提供更大容量的输电通道，使得风电基地盈余电量充分消纳，同时缓解负荷中心供电紧张的情况。

国内外研究人员对ATC的计算主要有确定性算法和概率性算法。确定性算法忽略系统中大量不确定因素，计算速度较快，但计算结果过于保守，适用于在线估算；而概率性的计算方法克服确定性方法的缺陷，充分地考虑设备运行状态、负荷的不确定性以及传输线路的容量等系统随机特征对ATC的影响，所得结果也更加符合实际情况。由于风电功率的随机性和间歇性会给风电并网系统的ATC计算增加更多不确定性，因此采用概率性的方法评估其对ATC的影响更为合适。文献［3］采用枚举法计算系统不同运行状态可能出现的概率，但不能考虑多个变量之间的相关性，很难适用到实际大型并网系统的研究；文献［4］重点研究了外送消纳风电时相关性对ATC的作用及ATC评估中不同电源调整策略的影响，但利用随机抽样生成风功率样本，存在较大的偶然性，样本的代表性难以保证；文献［5］采用蒙特卡洛模拟MCS（Monte Carlo Simulation）法对系统状态进行随机采样，在采样空间足够大的情况下得到较高的精度，但耗费时间过长；文献［6］基于拉丁超立方采样LHS（Latin Hypercube Sampling）的蒙特卡洛方法对输入随机变量的概率分布函数进行样本场景建模，却没有分析采样过程的稳定性和收敛性，且采样矩阵的排列计算过程繁琐。由此，研究人员将随机过程中的马尔科夫过程引入蒙特卡洛模拟法中，形成了马尔科夫链蒙特卡洛MCMC（Markov Chain Monte Carlo）模拟法，在保证精度的条件下大幅提高采样效率［7］。

根据已有研究表明，风电功率波动的概率密度分布曲线并非是单一特定的分布函数模型，具有多个极值点，即具有多峰值现象［8］。对于MCMC方法而言，通常一个概率峰值状态会吸引附近的状态转移到该峰值，这些状态包括这个峰值状态并称为一个模式（mode）。当分布十分陡峭且模式很多时，常用于构建马尔科夫链的Metropolis-Hastings采样和Gibbs采样算法很容易陷入某一个模式内部，并很难在模式之间进行状态转移，采样的结果陷入局部优化，这时的Metropolis-Hastings采样和Gibbs采样不再适用多峰值分布。由Tieleman等人提出的Tempered MCMC基于回火的MCMC采样算法［9］，以及基于自适应模式跳转AMH（Adaptive Mode-Hopping）MCMC 的限制玻尔兹曼机RBM（Restricted Boltzmann Machine）学习算法［10］有效解决了上述采样方法所遇到的困难，但不具备很强的应用性，这些采样过程产生的大量冗余计算以及采样的不稳定性往往成为其广泛应用的阻碍。

针对上述已有方法的不足，本文将切片反射采样RSS（Reflective Slice Sampling）［11］方法引入含风电并网系统的ATC评估中。通过加权高斯混合模型构建风电场出力的概率模型，采用RSS方法从概率模型函数中获取输入随机变量的样本空间；在计及含风电并网系统安全运行约束的条件下，将样本值代入潮流方程进行最优潮流计算求解ATC最大负载；最后对ATC的统计概率特征及其相关风险值曲线进行分析。在含有风电场接入的IEEE 30节点系统中分别对RSS方法和传统Gibbs采样方法进行仿真，结果表明本文所提方法具有评估效率高、收敛过程稳定和收敛速度较快等优点。

1 基于加权高斯混合分布的风电场概率模型

近年来，基于统计理论的概率密度函数法对风电场出力波动性及其量化分析的研究逐渐受到人们的关注，其核心思想是假定某一理论分布函数拟合风电功率波动的分布规律曲线，实现用已有的分布函数模型来近似描述风电功率的变化规律，以便对风电功率变化做进一步研究［12-13］。已有文献主要利用 Weibull分布［14］、t location-scal分布［15］、正态分布等对风电场出力进行拟合。本文以德国四大输网公司之一Amprion GmbH所负责的某区域的风电场实测数据 WMD（Wind Measurement Data）为样本［16］，数据周期为1 a，每点间隔15 min，共35040个数据点，得到风电功率概率密度分布。如图1所示，风电功率概率密度分布总体呈现下降趋势，但并非单调递减。单一分布函数不能对风电功率波动的概率密度分布特性所具有的“拖尾”性质进行准确拟合，拟合效果较差。因此，当风电场群“波动平滑效应”未能完全消除单个风电场的波动随机特性时，风电场群出力波动特性将不再满足某单一特定分布函数曲线。

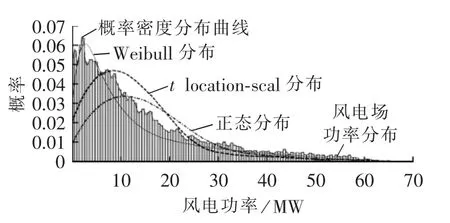
图1 单一分布函数模型拟合效果Fig.1 Fitting effect of single distribution function model

加权高斯混合分布WGMD（Weighted Gaussian Mixture Distribution）作为多个高斯分布函数的组合模型，可以平滑地近似描述许多复杂的数据分布，适用于拟合风功率波动的非线性概率密度分布特性。本文采用加权高斯混合模型来拟合图1实测风电功率概率密度分布，同时保留了风电场内部的非线性相关性。概率密度函数为：

其中，x为风电场出力实测数据；模型参数Θ=｛θm=（αm，bm，cm），m=1，2，…，M｝，M 为模型参数个数，αm、bm、cm分别为高斯混合模型m分量的权重和该权重高斯分布Gm（·）的均值、方差。通常高斯混合分布模型未知参数的估算方法有矩估计法和极大似然估计法。文献［17］采用了传统求解WGMD未知参数的EM（Expectation Maximization）算法。EM算法在求取加权高斯混合模型参数时受到初始条件的影响，输出结果不一定能够收敛到全局最优。

为克服EM算法的缺陷，本文采用DAEM（Deterministic Annealing Expectation Maximization）算法［18］，通过引入退火机制求取加权高斯混合模型中的未知参数，从而使最终的结果与实测数据计算结果之间的偏差减小。风电场功率的实测数据X就是观测数据，称为不完全数据，而每个风电场功率属于哪一类是不可观测的，令风电功率所属类别为ωϵ｛1，2，…，M｝，则完全数据为 H=｛hn=（xn，ωn），n=1，2，…，N｝，其中xn为第n个风电场出力实测数据，N为实测数据总个数。DAEM算法的参数估计具体步骤如下。

a.初始化迭代参数 Θ（0）和温度参数 β=βmin。

b.模型分布参数进行如下迭代，直到收敛。

其中，ωnm为风电实测数据第n个高斯模型m分量的隐含变量分别为高斯混合模型m分量基于第z次的迭代后第z+1次模型参数的权重和该权重高斯分布均值、标准差。

c.更新温度参数 β=ββrate，βrate为迭代步长，其取值范围为［1.1，1.5］。

d.如果β<1，则重复步骤b，否则停止。

2 RSS算法

本文基于Duane等人建立的混合蒙特卡洛（hybrid Monte Carlo）［19］法，提出一种属于汉密尔顿力学（Hamiltonian dynamics）均匀分布的特殊移动切片边界“反射”采样法。首先，假设风电场出力概率密度函数 f（x）及其梯度 h（x），给定初始采样值 x0，共采集 N 个采样值；其次，在区间［0，f（x）］均匀选取一个辅助变量y来确定切片S（切片S包含初始采样值x0）；引进动能变量p，表明当前在状态空间采样的移动方向和速度，p的选取服从标准正态分布且独立于变量x；最后，尺度参数w决定了每次沿变量p修正x的平均步长大小，xi+1=xiϵN+wp，形成精确边界反射采样，xiϵN为N次采样中的第i次采样值，采样过程如图2所示。

图2 精确边界反射采样示意图Fig.2 Schematic diagram of reflective sampling from exact boundary

若初始点x0沿着动能变量p以步长wp移动到边界之外，则需要适当改变p，使采样点沿着新的方向在切片内继续移动；直到当点xi碰撞到切片边界，此时，计算出碰撞点的梯度h，修改变量p。

理想的反射路径却很难实现，因为需要准确计算出当前路径与切片边界的交点。本文将介绍“内与外”2种反射方法来替代计算移动路径与边界碰撞点时需要的大量计算。

a.内反射移动过程：当从切片内采样点xi以步长wp移动到切片外xi+1=xi+wp时，不再计算移动轨迹与边界的交点，而是在边界内利用f（x）的梯度反射移动。通过验证点xi以同步长的相反方向移动，若终点仍然出界，则路径有效，xi+1即为采样值，如图3（a）所示；若反方向移动点同步长未出界，则重新设定变量p再次移动，如图3（b）所示。

图3 内反射采样示意图Fig.3 Schematic diagram of reflective sampling from inside point

内反射路径有效性k数学模型为：

b.外反射移动过程：同样，当采样路径进行到切片之外后，需要基于移动点处的梯度进行反射路径改变，如图4所示。经过一系列预设变量所决定的轨迹移动后，若终点停留在片内，则接受反射移动轨迹，终点即为采样值。尽管有时会导致路径不会重返切片内部而被拒绝，但随着转移次数的增加，最终会返回切片内部，形成有效的风电场出力采样值。

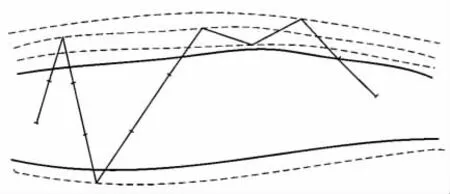
图4 外反射采样示意图Fig.4 Schematic diagram of reflective sampling from outside point

外反射路径有效性g数学模型为：

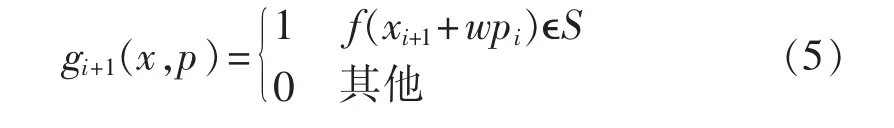
RSS方法具体迭代步骤如下。

a.给定初始采样点x0。

b.引入辅助变量 y，区间［0，f（x0）］均匀选取 y来确定切片S。

c.预定步长w，选取服从标准正态分布的动能变量p，完成采样初始变量设定。

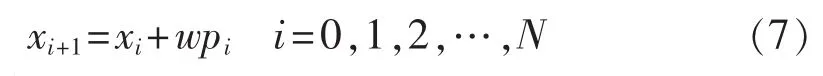
d.根据内外反射原理过程，不断更新变量p改变路径方向，如式（3）所示，进行反射采样。

e.判断路径有效性k＝1或g＝1是否成立，若成立，则路径有效，xi+1替换xi作为新的初始采样值进行下次迭代采样；若未同时成立，则路径无效，继续进行步骤d，直到获取新的采样值。

总体而言，在路径移动开始前会设定变量y、p和w，并且在迭代初期保持变量不变（除非由于反射改变p）。当使用内反射时，每一步均需要选择变量y，更新局部p；当使用外反射时，反射接受率随着预定步长w的不断优化而提高。

3 基于最优潮流的ATC评估

3.1 基于最优潮流计算ATC

ATC的计算主要由当前运行状态、约束条件及不确定性因素共同决定。本文的ATC计算中受电侧内负荷增长程度通过负荷因子λ来表达，λ达到最大的同时输电断面的输电功率也达到最大，即为ATC的值：

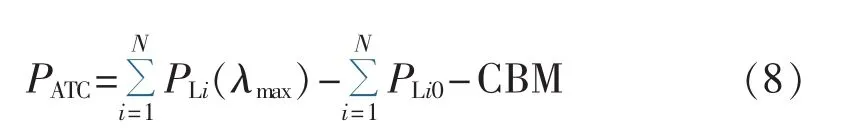
其中，PLi0为受电侧初始负荷值；PLi（λmax）为受电侧最大负荷值；容量效益裕度CBM（Capacity Benefit Margin）按最大输电能力TTC（Total Transfer Capability）的5%取值。求解负荷因子达到最大是一个优化问题。本文基于最优潮流OPF（Optimal Power Flow）进行求解，仅考虑发电机容量、节点电压及输电线路热极限等静态安全约束，简化为如下非线性优化模型：

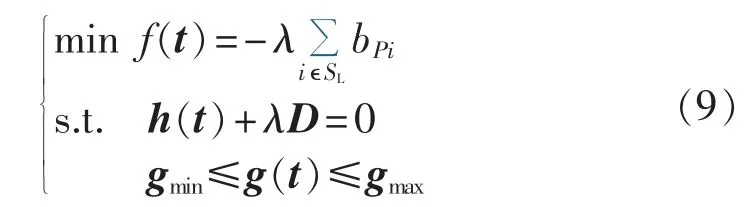
其中，t包含系统所有状态变量和控制变量；λ为负荷增长参数化标量；D=［bPbQ］T为负荷增长方向向量；SL为受电侧的负荷节点集合；h（t）为潮流方程等式约束条件；g（t）为静态安全约束所确定的不等式约束，gmax和gmin分别为其上、下限。

3.2 ATC评估指标

为了更准确地描述电网接入风电场后的输电能力，通过求取下列ATC概率统计特征和相关风险指标，以便量化风电并网对系统ATC的影响。

a.样本空间中ATC的均值、标准差、最大值、最小值等，以及统计分析方法得到累积分布函数。

b.在ATC计算结果中，不高于某一设定标准值TATC的累积概率，视为风险概率δRisk1：

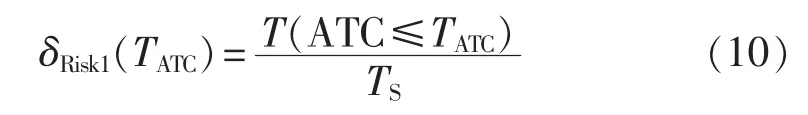
其中，TS为迭代的总次数；T为计算结果ATC不高于标准值TATC的数量。

c.除了考虑ATC不高于TATC的概率之外，ATC减少的总量（TATC－ATC）也需量化，即风险值 δRisk2计算如下：

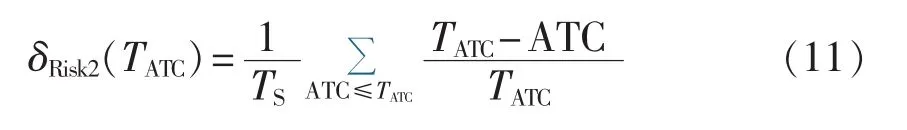
4 ATC评估算法的流程

a.根据第1节建立风电场出力概率模型，将风电场的出力实测数据 X= ｛x1，x2，…，xN｝代入 DAEM算法迭代公式，计算出风电场有功出力概率函数的未知参数。

b.分别采用RSS和Gibbs采样算法对风电场概率模型和服从正态分布的负荷模型进行采样，采样迭代次数按照变化系数波动范围确定。当变化系数小于预先设定值δ时，如式（12）所示，得到各样本空间稳定的马尔科夫链｛Pwind，Pload，Qload｝；同时，采用恒功率因数（cos φ=0.9）控制风力发电机组，得到风电场无功功率Qwind，完成构建潮流计算的样本变量空间。

其中，Var（ATC）为样本空间方差；E（ATC）为样本空间期望；本文取δ=0.0025。

c.利用概率统计方法得到ATC样本空间及风险各项指标，求取ATC期望E（ATC）（标幺值）的收敛曲线、ATC累积分布曲线以及ATC概率风险值δRisk1和δRisk2，进行采样方法比较及ATC风险评估。

5 算例分析

5.1 风电功率概率模型

通常高斯混合模型使用不超过5阶模型对目标分布建模，根据实测数据预估风电出力概率分布水平。本文分别采用2阶、5阶加权高斯混合模型得到拟合风电功率概率密度分布曲线如图5所示，表1给出了高斯混合模型的参数值。从图5可看出，随着加权阶数的增加，拟合精度也在提高。因此，本文风电场功率分布选取5阶模型进行拟合。

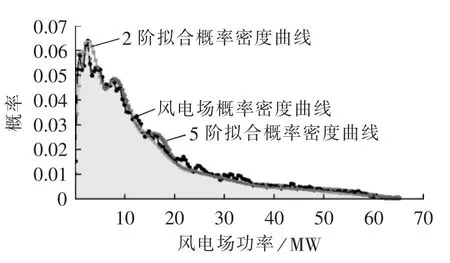
图5 风电功率波动的概率密度分布曲线拟合图Fig.5 Fitting curves of probability density distribution of wind power

表1 加权高斯混合模型的参数值Table 1 Parameters of weighted Gaussian mixture model

5.2 ATC风险评估方法的有效性

图6 含风电场的IEEE 30节点系统示意图Fig.6 IEEE 30-bus system with wind farm

本文在IEEE 30节点系统的节点15（PQ节点）接入风电场，如图6所示。基于MATLAB R2010a和PSAT电力系统计算工具包对修改后的系统进行仿真分析。系统常规发电的总装机容量为350MW，总负荷为283.4 MW，发电侧包含节点 1、2、11，负荷侧包含节点12、14、16。在无风电场接入系统情况下，依据式（3）和（4），ATC 仿真结果达到 52 MW，λmax为 2.69。

5.2.1 RSS方法的稳定性

为验证RSS方法的高效性和稳定性，利用RSS和Gibbs采样方法分别对风电场出力的概率密度函数采样，并对采样结果进行对比分析。根据MCMC模拟算法理论，若经过G次迭代采样得到的马尔科夫链收敛于平稳分布，舍去前g次采样（或称为“退火”）即为样本空间结果。

图7为2种采样方法生成的E（ATC）（标幺值）收敛曲线。如图7所示，RSS方法相互独立的3条马尔科夫链经过1300次迭代（“退火”）后，收敛结果趋于稳定，收敛曲线的变化系数小于设定值δ，且收敛过程波动范围较小；而Gibbs采样方法相互独立的3条马尔科夫链需要经过3000次迭代（“退火”）后，结果才趋于收敛，且每条链收敛过程波动范围较大。由此可以得知，与Gibbs采样算法相比，RSS算法在整个采样过程有较高的稳定性和较好的收敛性。

图7 2种采样方法生成的E（ATC）收敛曲线Fig.7 Convergence plots of E（ATC）by two sampling methods

5.2.2 RSS方法的精确性

本文以WMD作为RSS和Gibbs采样方法统计结果对比的标准数据源。表2给出了各采样算法与WMD计算结果相对误差和计算时间的比较。就计算时间而言，WMD由于数据空间的庞大，导致计算时间过长；而RSS与Gibbs采样所用时间较为相近，因此，将着重比较分析采样结果计算后的ATC样本空间数据。本文经“退火”收敛后的样本空间数据均取5 000个，与WMD的统计计算结果比较，Gibbs采样的均值远小于标准计算，标准差较大，后文将对该问题做出分析；RSS的均值和标准计算很接近，标准差误差也较小，满足应用的实际要求，由此验证了RSS算法的精确性。

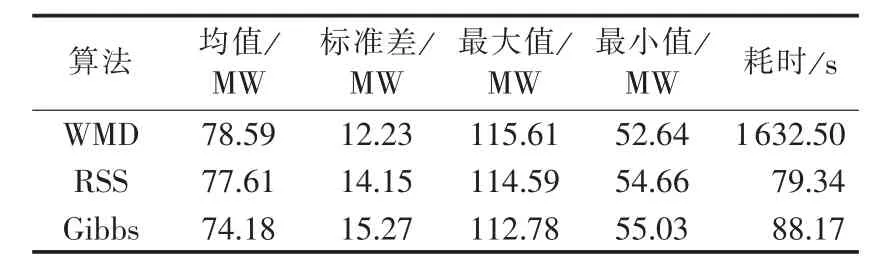
表2 不同采样算法的ATC统计指标对比Table 2 Comparison of ATC statistical indexes among different sampling methods

图8给出了不同数据来源结果的ATC累积分布曲线。由于Gibbs采样算法未能对风电功率波动的概率密度分布特性所具有的“拖尾”性质准确采样，因此不能准确反映目标函数分布，对模型的拟合曲线存在严重偏差，与标准计算结果的ATC累积分布曲线误差较大，验证了样本均值偏小、ATC计算后的样本空间趋于保守的结果；RSS优化了采样过程，保持了采样空间与目标分布的准确性，与WMD的累积分布曲线几乎完全重合，由此反映了RSS算法较Gibbs采样算法在整个采样过程有较高的精确性。

图8 ATC的累积分布曲线Fig.8 Cumulative distribution curves of ATC

5.2.3 基于概率风险分析的ATC评估

根据第3节的风险评估求解方法，对RSS和Gibbs采样方法所得到的样本空间进行ATC风险评估统计，得到如图9、10所示的风险水平随ATC的变化趋势。

图9 基于风险值δRisk1的风险变化Fig.9 Variation of δRisk1

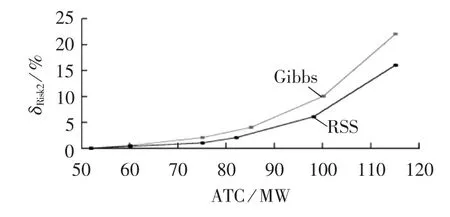
图10 基于风险值δRisk2的风险变化Fig.10 Variation of δRisk2

由图9可以看出，当ATC达到80 MW时，RSS的风险值δRisk1水平较低；当风险值δRisk1达到60%时，Gibbs采样的ATC结果为78.62MW，而RSS的ATC结果为90 MW。原因是Gibbs对风电场概率模型采样相对RSS较为保守，风电出力并入系统的采样值偏小，使得Gibbs采样方法所得的ATC低于标准值的数量较多，导致风险值δRisk1总体水平偏高。同时，2种采样的风险值曲线显示了在ATC达到62MW，即ATC容量增加12%时，δRisk1随之增长近25%；ATC从90MW增加到115MW时，δRisk1随之增加15%～18%，这样的线性风险曲线信息可以让调度人员针对电网情况选择合适的风险值，进而提高电力传输能力。

图10中的风险值δRisk2曲线体现了2种采样算法的ATC减少总量风险值δRisk2的量化走势。RSS所得ATC结果比Gibbs采样方法更接近标准值，随之产生的δRisk2的值较低，并且随着ATC容量的增涨，Gibbs采样结果的风险值δRisk2会有明显骤增的趋势，符合风险值δRisk1及第5.1节中ATC累积分布曲线的结论。因此，算例中通过ATC期望E（ATC）的收敛曲线、ATC累积分布曲线以及概率风险分析的ATC评估充分说明，RSS能够稳定收敛，显著提高了采样精准度，进而可以在考虑电力系统运行调度状态下选择合适的风险阈值，充分提高风电并网效率。

6 结论

本文通过多个高斯分布函数的组合模型验证了加权高斯混合分布适用于拟合风电功率波动的非线性概率密度分布特性的有效性。采用RSS对MCMC方法中常用的Gibbs采样算法进行改进，克服了采样过程会陷入局部优化的弊端，有效提高了采样效率。对通过潮流计算采样后的风电场样本空间，进行ATC统计分析，验证了RSS的高效性及精确性。本文结论是基于德国某风电场实测数据分析得到的，后续将增加多数据源对本文方法的普适性进行验证，同时针对电力系统突发事件的风险评估做进一步分析与研究。

参考文献：

［1］UECKERDT F，BRECHA R，LUDERER G.Analyzing major challenges of wind and solar variability in power systems［J］.Renewable Energy，2015，81：1-10.

［2］Transmission Transfer Capability Task Force.Available transfer capability definitions and determination［R］.Princeton，NJ，USA：North American Electric Reliability Council，1996.

［3］XIA F，MELIOPOULOS A P S.A methodology for probabilistic simultaneous transfer capability analysis［J］.IEEE Transactions on Power Systems，1996，11（3）：1269-1278.

［4］栗峰，王建学，程海花.面向新能源外送消纳的区域间概率可用传输能力计算［J］. 电网技术，2016，40（2）：348-353.LI Feng，WANG Jianxue，CHENG Haihua.Probabilistic calculation ofinterregionalavailable transfercapability aiming ataccommodating renewable energy［J］.Power System Technology，2016，40（2）：348-353.

［5］DUFO-LÓPEZ R，PÉREZ-CEBOLLADA E，BERNAL-AGUSTÌN J L，et al.Optimisation of energy supply at off-grid healthcare facilities using Monte Carlo simulation［J］.Energy Conversion and Management，2016，113：321-330.

［6］罗钢，石东源，蔡德福，等.计及相关性的含风电场电力系统概率可用输电能力快速计算［J］.中国电机工程学报，2014，34（7）：1024-1032.LUO Gang，SHI Dongyuan，CAI Defu，et al.Fast calculation of probabilistic available transfer capability considering correlation in wind power integrated systems［J］.Proceedings of the CSEE，2014，34（7）：1024-1032.

［7］ALMUTAIRI A，AHMED M H，SALAMA M M A.Use of MCMC to incorporate a wind powermodelfor the evaluation of generating capacity adequacy［J］.Electric Power Systems Research，2016，133：63-70.

［8］申颖，赵千川，李明扬.多时空尺度下风电平滑效应的分析［J］.电网技术，2015，39（2）：400-405.SHEN Ying，ZHAO Qianchuan，LI Mingyang.Analysis on wind power smoothing effect in multiple temporal and spatial scales［J］.Power System Technology，2015，39（2）：400-405.

［9］FISCHER A，IGEL C.A bound for the convergence rate of parallel tempering for sampling restricted Boltzmann machines［J］.Theoretical Computer Science，2015，598：102-117.

［10］FARR W M，MANDEL I，STEVENS D.An efficient interpolation technique for jump proposals in reversible-jump Markov chain Monte Carlo calculations［J］.Royal Society Open Science，2015，2（6）：150030.

［11］NEAL R M.Slice sampling［J］.Annals of Statistics，2003，31（3）：705-741.

［12］刘兴杰，谢春雨.基于贝塔分布的风电功率波动区间估计［J］.电力自动化设备，2014：34（12）：26-31.LIU Xingjie，XIE Chunyu.Wind powerfluctuation interval estimation based on beta distribution［J］.Electric Power Automation Equipment，2014，34（12）：26-31.

［13］江岳文，温步瀛.结合风电功率超短期预测值偏差的实时市场调度［J］. 电力自动化设备，2015：35（3）：12-17.JIANG Yuewen，WEN Buying.Real-time market dispatch based on ultra-short-term forecast error of wind power［J］.Electric Power Automation Equipment，2015，35（3）：12-17.

［14］MOHAMMADI K，ALAVI O，MOSTAFAEIPOUR A，et al.Assessing different parameters estimation methods of Weibull distribution to compute wind power density［J］.Energy Conversion and Management，2016，108：322-335.

［15］林卫星，文劲宇，艾小猛，等.风电功率波动特性的概率分布研究［J］. 中国电机工程学报，2012，32（1）：38-46.LIN Weixing，WEN Jinyu，AI Xiaomeng，et al. Probability density function of wind power variations［J］.Proceedings of the CSEE，2012，32（1）：38-46.

［16］Grid data［EB／OL］. ［2016-09-10］.https：∥www.amprion.net／Grid-Data／Wind-Feed-In ／.

［17］蔺红，孙立成，常喜强.新疆风电出力波动特性的概率建模［J］.电网技术，2014，38（6）：1616-1620.LIN Hong，SUN Licheng，CHANG Xiqiang.A probabilistic model to simulate wind power output fluctuation of a certain wind farm cluster in Xinjiang region［J］.Power System Technology，2014，38（6）：1616-1620.

［18］GAO J，ZHOU L，DU B.Parameter estimation of Gaussian mixture model and its application in multimode process monitoring［C］∥2016 12th World Congress on Intelligent Control and Automation（WCICA）. ［S.l.］：IEEE，2016：2896-2901.

［19］DUANE S，KENNEDY A D，PENDLETON B J，et al.Hybrid Monte Carlo［J］.Physics Letters B，1987，195（2）：216-222.