基于遗传算法的魔术公式轮胎模型参数两级辨识

边 伟，龚佳慧，文爱民，陈林山，刘奕贯，

(1.南京交通职业技术学院 汽车工程学院，江苏 南京 211188；2.南京农业大学 工学院，江苏 南京 210031)

基于遗传算法的魔术公式轮胎模型参数两级辨识

边 伟1，龚佳慧2，文爱民1，陈林山1，刘奕贯1，2

(1.南京交通职业技术学院 汽车工程学院，江苏 南京 211188；2.南京农业大学 工学院，江苏 南京 210031)

为了提高魔术公式(Magic formula，MF)轮胎模型参数的辨识精度及速度，采用参数的两级辨识的方法，定义公式相关的参数B，C，D，E为一级参数，轮胎模型的特性参数为二级参数。首先基于Matlab遗传算法工具箱对一级参数进行辨识，然后基于一级参数的辨识结果再次利用遗传算法对二级参数进行辨识，并且将辨识出的参数带入到魔术公式计算轮胎的受力，拟合出不同载荷下的魔术公式轮胎模型的纵向力随滑移率变化曲线。对一级参数辨识的相对残差为2.196 8%，且遗传代数为40代左右就收敛；二级参数的辨识相对残差为0.840 3%，且遗传代数为20代左右时就收敛。辨识结果表明：对魔术公式轮胎模型参数分两级辨识的方法，可以保证参数辨识的精度，并有效提高辨识的效率,为实时参数辨识提供了高效可靠的方法。

车辆工程；轮胎模型；魔术公式；遗传算法；参数辨识

轮胎是汽车的重要部件，作为汽车与路面的支撑和传递单元，其力学特性的好坏直接影响汽车的平顺性、操纵稳定性、制动性、安全性等。因此，建立与简化合理的轮胎动力学模型对轮胎新型产品的开发以及对汽车整车性能的分析具有重要的意义[1]。轮胎模型的研究经历了从静态到动态，从稳态到非稳态，从线性到非线性的过程。轮胎模型可划分为理论轮胎模型、经验轮胎模型和自适应轮胎模型[2-3]。目前，在操纵稳定性研究分析中用得较多的为魔术轮胎经验模型、Fiala轮胎理论模型以及UA轮胎理论模型。

魔术公式(Magic formula，MF)轮胎模型能够精确地描述轮胎的力学特性，因此在车辆动力学研究领域被广泛采用。目前，对MF轮胎模型参数辨识的方法有多种。宋晓琳等[4]基于改进的粒子群优化算法对轮胎参数进行了辨识；王丹等[5]，田晶晶等[6]都基于遗传算法对其参数进行辨识；杨峰[7]基于Excel Solver对多种常用轮胎模型参数进行辨识，其中包MF轮胎模型；J.A.CABRERA等[8]使用协同进化算法对MF轮胎模型参数进行辨识。遗传算法鲁棒性强，可以在全局范围内应用，受初值影响较小，因此被广泛使用[9-10]。从研究结果来看，田晶晶等利用遗传算法辨识的精度较高，但是迭代次数很多，即辨识速度慢，而王丹等辨识的精度较低。考虑到MF 轮胎模型的参数较多，且高度非线性，是导致辨识速度慢、精度低的主要原因。笔者提出两级参数辨识的方法，定义公式相关的参数峰值因子、形状因子、刚度因子、曲率因子为一级参数，轮胎模型的特性参数为二级参数，分别采用遗传算法对一级、二级参数进行辨识，并用迭代次数和辨识精度验证遗传算法两级辨识MF模型参数的优越性。

1 魔术公式轮胎模型

魔术公式是以三角函数为基础，以统一形式表达纵向力Fx、侧向力Fy、回正力矩Mz、翻转力矩Mx、滚动阻力矩My等之间的关系。魔术公式轮胎模型的输入和输出如图1。

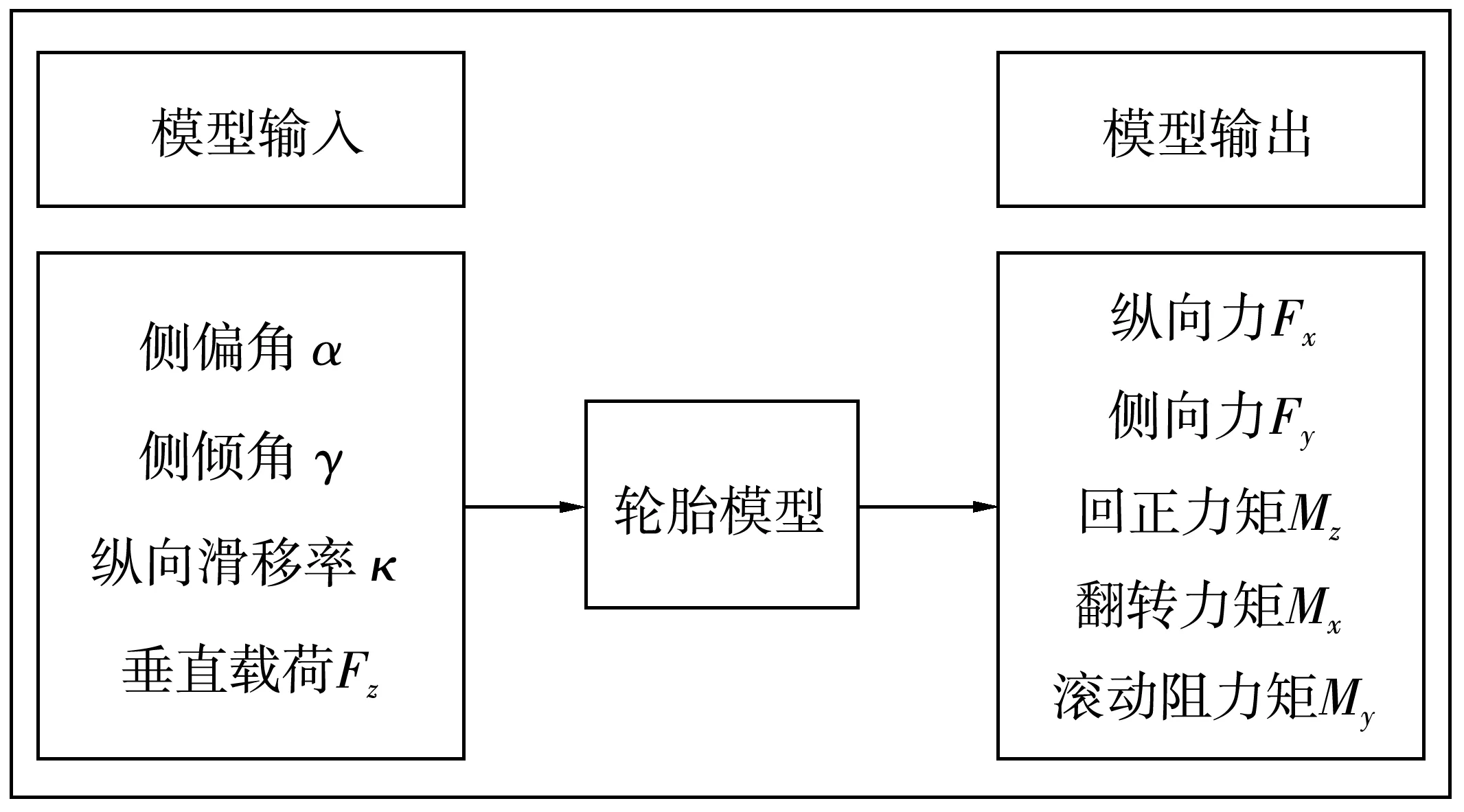
图1 魔术公式轮胎模型的输入输出Fig.1 Input and output of magic formula tire model

此外，MF轮胎模型是基于实验测得的数据，辨识出模型相关参数，从而得到相应的魔术公式轮胎模型，并且可以运用辨识的模型计算轮胎其他各种工况下的受力。

MF轮胎模型计算力与力矩的总体表达式为[11]

Y(x)=Dsin{C·arctan[Bx-E(Bx-arctan(Bx))]}

(1)

式中：Y(x)是纵向力、侧向力或者回正力矩；D是峰值因子，决定了曲线峰值；B是刚度因子，决定了原点处斜率；C是形状因子，控制着曲线形状；E是曲率因子，影响着曲线峰值以及渐近线附近的曲率。

笔者以Pacejka’89轮胎纵向力魔术公式的参数辨识过程为例进行分析。Pacejka’89轮胎纵向力计算公式为[12]

Fx=Dsin{Carctan[BX1-E(BX1-arctan(BX1))]}+Sv

(2)

其中：

2.2 两组患者心室重构指标比较 治疗前，两组患者的心室重构指标均明显异常；治疗后，两组的心室重构指标均明显改善，且观察组改善程度较地高辛组更明显，差异有统计学意义(P<0.05)。见表1。

X1=k+Sh

(3)

C=b0

(4)

(5)

(6)

(7)

(8)

Sh=b9Fz+b10

(9)

Sv=0

(10)

式中：X1是纵向力组合自变量；k为纵向滑移率；Sv是曲线垂直方向漂移；Sh是曲线水平方向的漂移。

纯纵滑工况下纵向力计算公式需要辨识的参数共有11个，如表1[7]。

表1 轮胎纵向力魔术公式待辨识的参数Table 1 Parameters to be identified of the magic formula of tire longitudinal force

2 利用遗传算法进行参数辨识的过程

遗传算法操作使用适者生存的原则，把问题的参数用基因表示，把问题的解用染色体表示，从而得到一个由具有不同染色体的个体组成的群体。它通过选择淘汰，突然变异，基因遗传等规律产生适应环境变化的优良后代，经过遗传迭代，最终得到最优解。其本质是一种高效、并行、全局搜索的方法，具有高速收敛性和较高的鲁棒性[13]。

利用遗传算法寻找最优解的过程首先是将需要辨识的参数编码成由n位{0,1}组成的基因组，则解的精度取决于n的大小。所有参数的基因组形成一个行向量，代表了一条染色体，而一条染色体代表一个个体。第一代即初始种群是随机产生的，初始种群代表着初始解，这些解的优劣，需要通过计算其适应度值，根据适应度值来评估这些解。定义此次参数辨识过程的目标函数为

(11)

其物理意义是将识别得到的参数带入到魔术公式轮胎模型中，相同的滑移率下，魔术公式轮胎模型的计算结果与实验测得的数据差值的平方和。y(x)是由魔术公式轮胎模型计算得到的纵向力，而ytest是实验数据。显然，目标函数值越小，则对应的解更优，即希望较小目标函数值对应的解的适应度值高。这一步可以通过基于排序的适应度分配函数得到。

种群的进化过程则是逼近最优解的过程，进化过程主要包括遗传算子的选择、交叉、变异。为了降低选择的误差，同时又要遵循“优胜劣汰”的自然法则，即越优的解被保存的概率就越大，因此选用随机遍历选择方法。将选择出的染色体进行复制，作为交叉和变异的父代。

遗传算子交叉时，父代中的染色体两两一组进行交叉，交叉的概率Pc∈[0.4～0.99]。两点交叉是指交叉点为2个的交叉方式，而交叉点位置是通过随机数确定的。交叉时两个交叉点的基因段互换，交叉过程如图2。

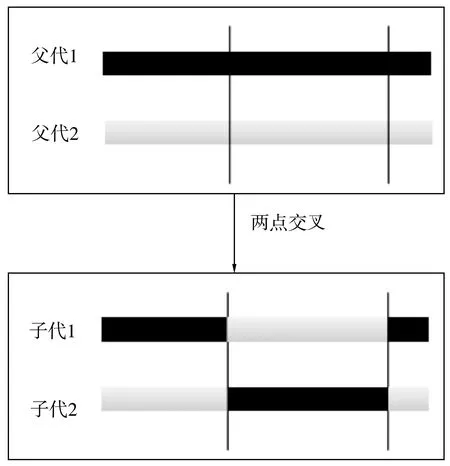
图2 两点交叉运算示意Fig. 2 Two-point crossover operation schematic

变异是染色体上的某个或者某些基因的值发生改变，根据编码的特点，变异其实就是染色体上某一位或者某些位“0”变为“1”或者“1”变为“0”。变异的基因位是以一较小的概率随机产生的，变异概率Pm∈[0.000 1～0.1]，变异过程如图3。变异是寻优过程中的重要步骤，不仅可以避免选择和交叉带来的一部分信息的丢失，提高遗传算法的全局和局部搜索能力，而且能够保持种群的多样性，防止早熟现象的出现。

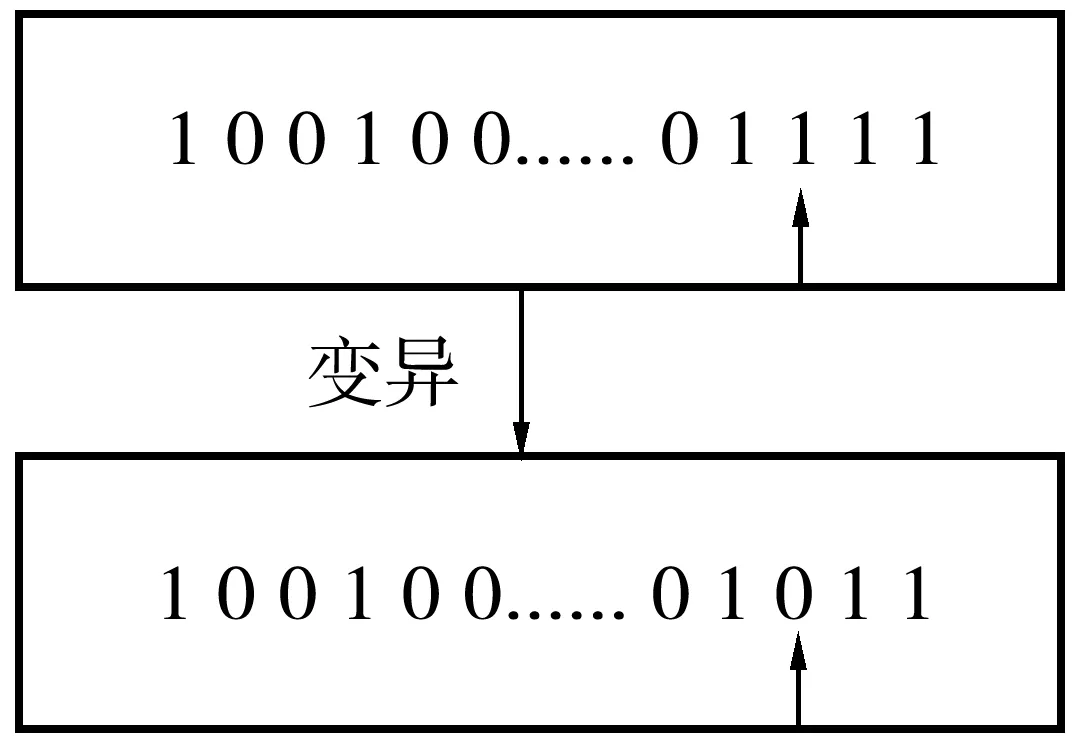
图3 变异运算示意Fig. 3 Mutation operation schematic

经过选择、交叉、变异得到子代，并将其转化为十进制数带入到目标函数，得到子代各个体的适应度值，按照代沟的比例，将子代中个体按照适应度值从高到低插入父代种群中，形成新种群，再计算新种群适应度值，进行选择、交叉、变异。这样不断重复上述过程，最终得到最优结果，终止条件是遗传代数最大值。整个参数辨识过程流程如图4。

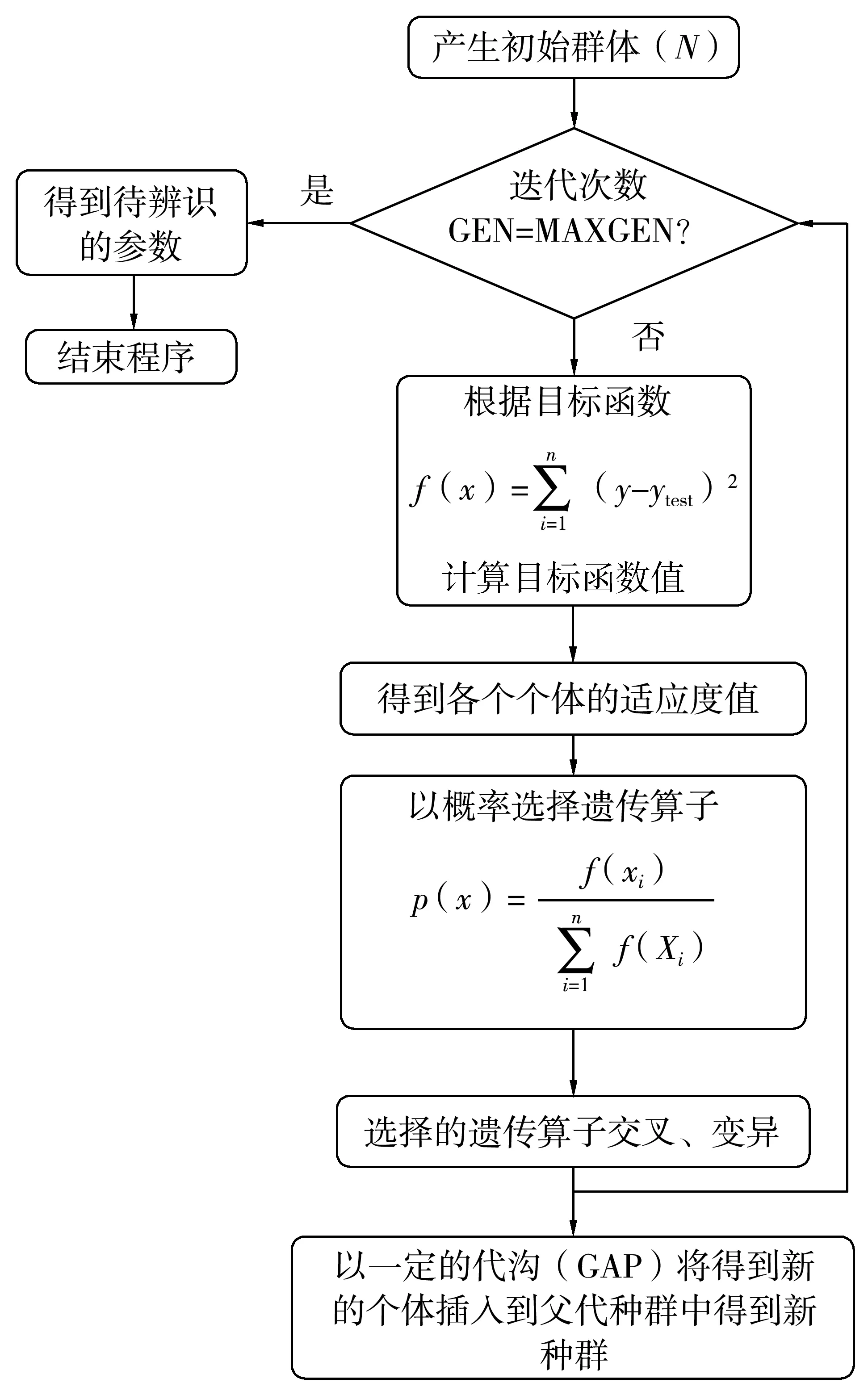
图4 基于遗传法的魔术公式参数辨识流程Fig.4 Flow chart of parameter identification of magic formula based on genetic algorithm

3 魔术公式轮胎模型参数辨识的结果

3.1 魔术公式轮胎模型一级参数的辨识

笔者利用文献[8]中的实验数据组作为参数辨识的实验数据。选取轮胎的垂向载荷分别为Fz=3 020 lb，Fz=6 040 lb，Fz=9 060 lb时的数据，如表2。

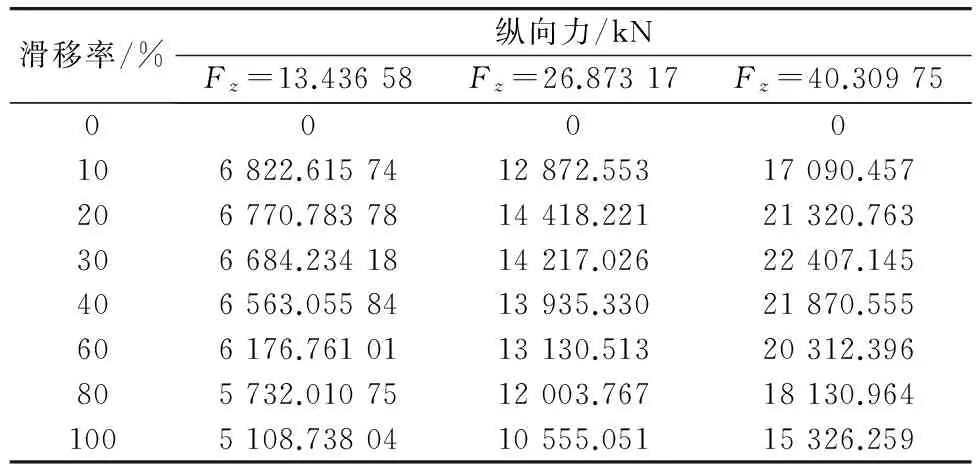
表2 参数辨识使用的实验数据

笔者利用遗传算法辨识魔术公式轮胎模型一级参数时算法相关参数的设置为：初始种群N=2 000，最大遗传代数为MAXGEN=100，交叉概率Pc=0.7，变异概率Pm=0.01，代沟GAP=0.95，即遗传算法辨识过程中父代中将有95%的个体被子代中的优秀个体替换。

车轮的外倾角是车轮平面与坐标系的垂直轴的夹角，假设为理想情况，不考虑车轮的外倾角和漂移，即侧倾角γ，Sh，Sv均为0，对魔术公式轮胎模型公式相关的参数进行辨识，辨识过程中实验数据的残差进化过程如图5。由图5可看出遗传迭代到第40代时，结果都已经趋于收敛，说明遗传算法在辨识一级参数时的速度很快。

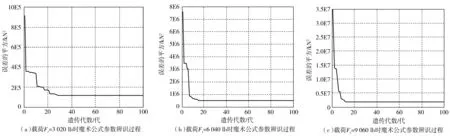
图5 基于遗传算法的MF轮胎模型一级参数辨识过程Fig. 5 Process of first level parameters identification of MF tire model based on genetic algorithm

根据一级参数辨识结果拟合出不同载荷下魔术公式轮胎模型纵向力随滑移率变化的曲线如图6。原始数据与遗传算法计算结果基本吻合，证明了基于遗传算法对魔术公式轮胎模型参数辨识的有效性。

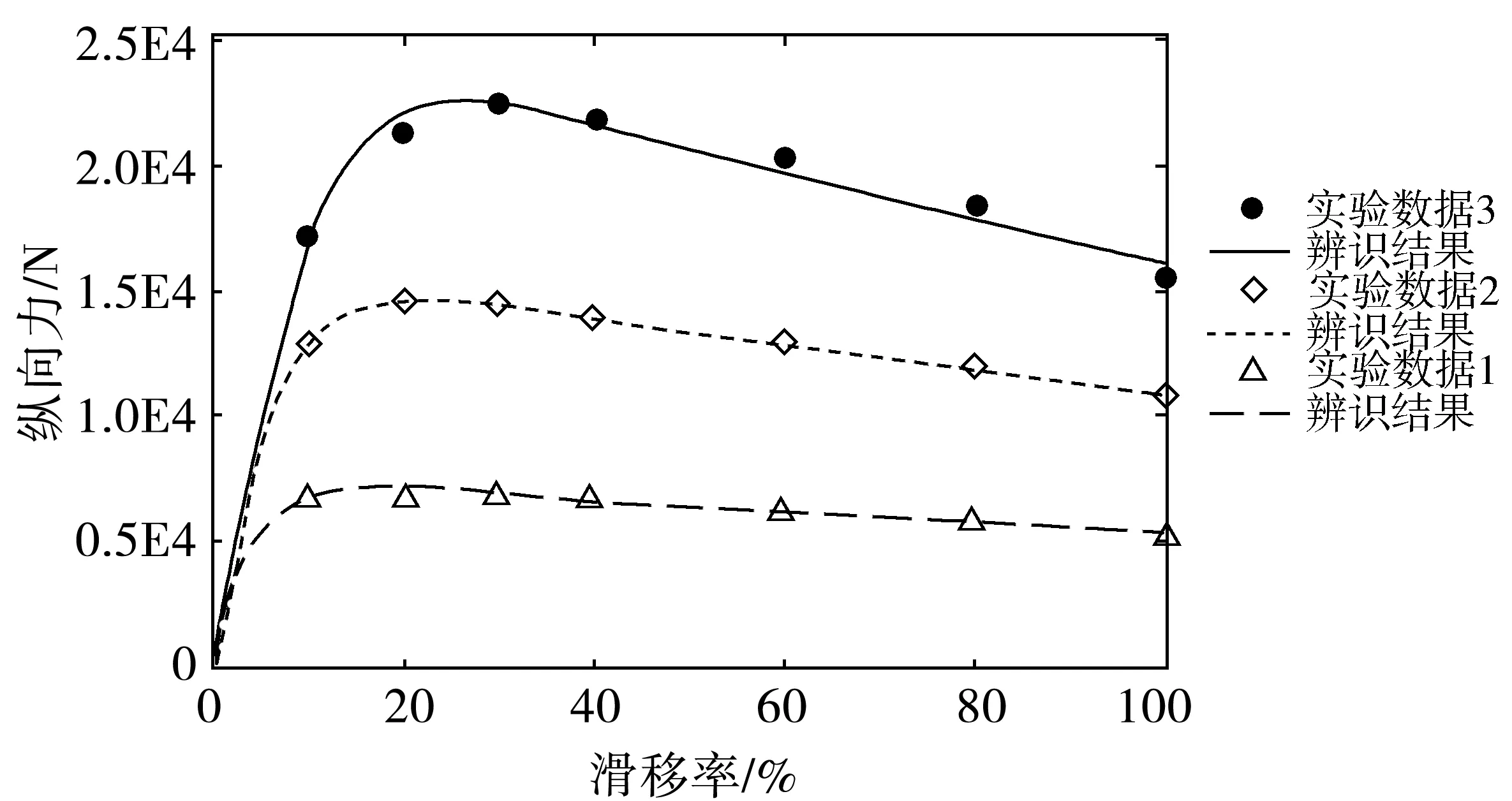
图6 基于遗传算法的魔术公式纵向力法拟合曲线Fig. 6 Fitting curve of magic formula longitudinal force based on genetic algorithm

为了进一步研究轮胎模型辨识效果，引入相对残差作为辨识精度的评价指标：

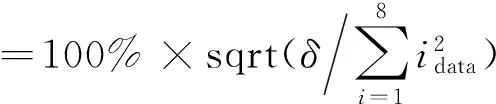
(12)

式中：δ为辨识残差，即拟合的魔术公式轮胎模型得到的值与实验数据之间的误差的平方之和；idata是试验数据点。

显而易见，相对残差越小，辨识精度越高。相关参数辨识结果如表3。

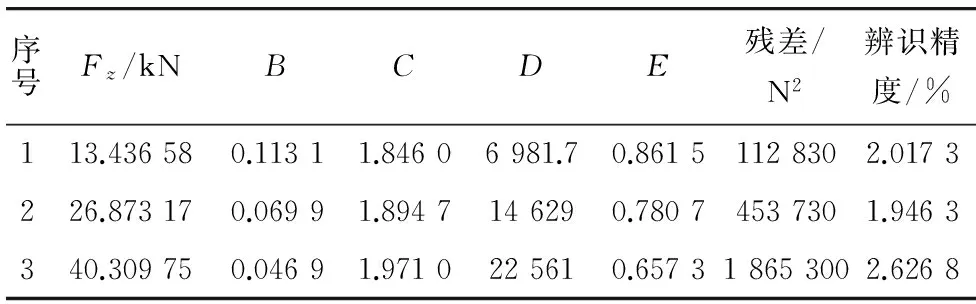
表3 魔术公式轮胎模型一级参数辨识结果Table 3 First level parameter identification results of magic formula tire model

根据表4的辨识结果，可以得出魔术公式轮胎模型一级参数的辨识过程全局辨识残差为810 620 N2，全局辨识精度为2.196 8%。

3.2 魔术公式轮胎模型二级参数辨识

对魔术公式二级参数即b0～b10辨识时，利用表4的辨识结果，根据式(3)～式(10)，基于遗传算法对其进行辨识。辨识的方法和算法相关参数的设置与一级参数的辨识过程一致。通过分析可得二级参数的辨识顺序为峰值因子参数、刚度因子参数、曲率因子参数。以峰值因子参数的辨识为例，由于D是关于Fz的二次函数，利用不同载荷下所辨识出来的D参数的值，可以较好地辨识出b1，b2的值。同理按顺序可以辨识出b3～b10的参数，辨识结果如表4，并得到遗传迭代变化如图7。

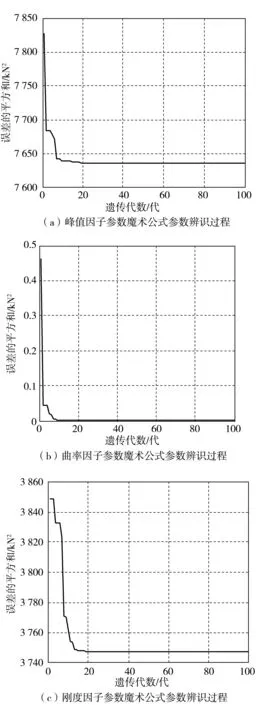
图7 基于遗传算法的魔术公式轮胎模型二级参数辨识过程Fig. 7 Process of second level parameters identification of MF tire model based on genetic algorithm

表4 MF轮胎模型二级参数辨识结果

Table 4 Secondary parameter identification results of MF tire model

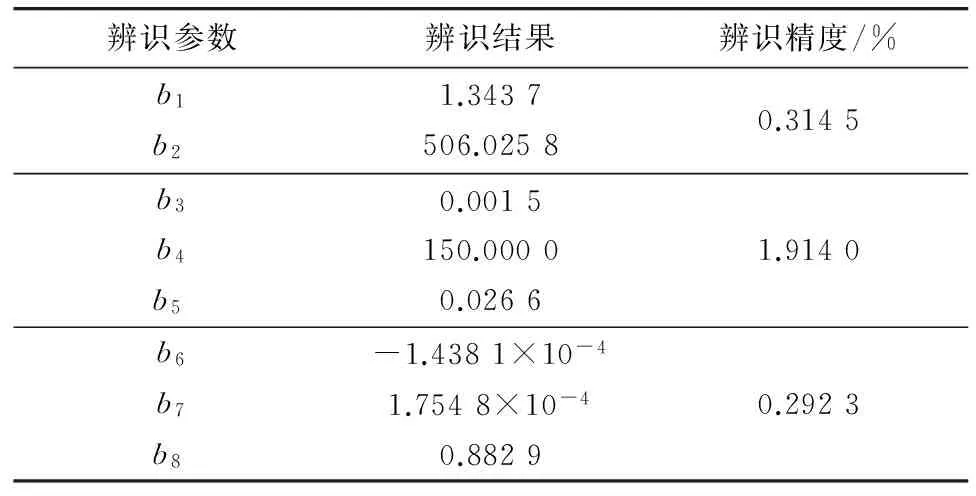
辨识参数辨识结果辨识精度/%b1b21.3437506.02580.3145b3b4b50.0015150.00000.02661.9140b6b7b8-1.4381×10-41.7548×10-40.88290.2923

对峰值因子参数、刚度因子参数、曲率因子参数辨识的精度分别为0.314 5%，1.914 0%，0.292 3%，辨识精度很高。同时，由辨识过程遗传迭代图分析得出，利用遗传算法对二级参数辨识时，迭代到20代左右的时候解就已经收敛，辨识速度很快。分级辨识的好处就是可以快速地辨识出相关的参数，并且在一次性对全部的参数进行辨识的时候很容易出现早熟现象，分级辨识时，每次辨识的参数较少，可以有效避免早熟现象的出现。

4 结 论

1)根据魔术公式轮胎模型公式相关参数以及待辨识的参数之间的关系，可将参数分级，先后用遗传算法对一级参数公式相关的参数和二级参数峰值因子参数、形状因子参数、刚度因子参数、曲率因子参数进行辨识。

2)完成一级参数的辨识，拟合出魔术公式轮胎模型纵向力随滑移率的变化曲线，拟合曲线上的数据点与试验的数据点基本吻合，辨识精度为2.196 8%。二级参数辨识的精度为0.840 3%，辨识精度较文献[4]有较大的提高。

3)分析辨识过程遗传迭代图，一级参数、二级参数的辨识结果都能在40代内收敛。证明了基于遗传算法对魔术公式轮胎模型参数分两级辨识的方法在保证辨识精度的情况下大大提高了辨识的速度，对于研究周期的缩短有重要意义，并且为参数的实时在线辨识提供了快速有效的方法。

[1] 任光胜.用Magic Formula对轮胎特性曲线的拟合与优化[J].重庆大学学报(自然科学版)，2001, 24(3)：22-25. REN Guangsheng. Optimization of curve fitting used in development of Magic Formula tire model[J].JournalofChongqingUniversity(NaturalScience), 2001, 24(3): 22-25.

[2] 马晓.不同轮胎模型对重型载货汽车整车性能仿真的影响分析[D].长春：吉林大学，2013. MA Xiao.AnalysisofInfluenceofDifferentTireModelsonPerformanceSimulationforHeavy-dutyTruck[D]. Changchun: Jilin University, 2013.

[3] 张云清，陈伟，陈立平，等.Magic Formula轮胎模型参数辨识的一种混合优化方法[J].汽车工程，2007，29(3):250-255. ZHANG Yunqing, CHEN Wei, CHEN Liping, et al. A hybrid optimization on parameters identification for Magic Formula tire model[J].AutomotiveEngineering, 2007, 29(3): 250-255.

[4] 宋晓琳，李红，郭孔辉.基于改进的粒子群优化算法的轮胎参数辨识[J].科技导报，2011，29(9)：53-56. SONG Xiaolin, LI Hong, GUO Konghui. Parameter identification of the tire model based on an improved particle swarm optimization algorithm[J].Science&TechnologyReview, 2011, 29(9): 53-56.

[5] 王丹，何乐，孙秀静，等.利用遗传算法识别汽车轮胎魔术公式参数[J].客车技术与研究，2015，37(2):1-4. WANG Dan, HE Le, SUN Xiujing, et al. Parameters identification of Magic Formula of vehicle tire using genetic algorithm[J].Bus&CoachTechnologyandResearch, 2015, 37(2): 1-4.

[6] 田晶晶，阳东波，李枭.基于遗传算法的魔术公式轮胎模型参数辨识方法研究[J]. 交通节能与环保，2014(4):13-16. TIAN Jingjing, YANG Dongbo, LI Xiao. Study on the parameters identification method of Magic Formula tire model based on genetic algorithm[J].EnergyConservation&EnvironmentalProtectioninTransportation, 2014(4):13-16.

[7] 杨峰.基于Excel Solver的常用稳态轮胎模型参数辨识[D].长春：吉林大学，2011. YANG Feng.ParametersIdentificationforCommonStead-StateTireModelsBasedonExcelSolver[D].Changchun: Jilin University,2011.

[8] CABRERA J A, ORTIZ A. A co-evolutionary algorithm for tire model parameters identification[J].StructuralandMultidisciplinaryOptimization, 2010, 41(5): 749-763.

[9] 雷英杰.MATLAB遗传算法工具箱及应用[M].西安：西安电子科技大学出版社，2004: 6-9. LEI Yingjie.MATLABGeneticAlgorithmToolboxandItsApplication[M]. Xi’an: Xidian University Press, 2004:6-9.

[10] 边霞，米良.遗传算法理论及其应用研究进展[J].计算机应用研究，2010,27(7):2425-2429. BIAN Xia, MI Liang. Development on genetic algorithm theory and its applications[J].ApplicationResearchofComputers, 2010, 27(7): 2425-2429.

[11] WEI Y T，OERTEL C，SHEN X L. Tyre rolling kinematics and prediction of tyre forces and moments: part II-simulation and experiment[J].VehicleSystemDynamics, 2012, 50(11): 1689-1706.

[12] 韦尧兵，赵学美，姜祖啸.纯工况和联合工况下MF-Tyre模型的参数辨识[J].山东理工大学学报(自然科学版)，2010,24(2):7-11. WEI Yaobing, ZHAO Xuemei, JIANG Zuxiao. Parameters identification for MF-Tyre model under pure and combined slip conditions[J].JournalofShandongUniversityofTechnology(NaturalScienceEdition), 2010, 24(2):7-11.

[13] 张雷，牛玉广，淮小利.基于LabVIEW的遗传算法辨识系统设计与应用[J].华北电力大学学报，2008，35(2)：51-56. ZHANG Lei, NIU Yuguang, HUAI Xiaoli. Design and application research of genetic algorithm identification system based on LabVIEW[J].JournalofNorthChinaElectricPowerUniversity, 2008, 35(2): 51-56.

(责任编辑：谭绪凯)

Two Levels of Parameter Identification of Magic Formula Tire Model Based on Genetic Algorithm

BIAN Wei1, GONG Jiahui2, WEN Aimin1, CHEN Linshan1, LIU Yiguan1，2

(1.College of Automobile Engineering, Nanjing Communications Institute of Technology, Nanjing 211188, Jiangsu, P. R. China;2.College of Engineering, Nanjing Agricultural University, Nanjing 210031,Jiangsu, P. R. China)

To improve the identification accuracy and speed of magic formula (MF) tire model, a method that dividing all parameters into two levels was used. The formula-related parametersB,C,D,Ewere defined as the first level parameters and the characteristic parameters of the tire model as the second level. Firstly, the first level parameters were identified by Matlab genetic algorithm toolbox, and then the second level parameters were identified by genetic algorithm again based on the former results. At the same time, the identification results were brought into the magic formula to calculate the tire force, and then the curve of longitudinal force of MF tire model changing with slip rate under different loads was fitted. The identification result shows that the relative residual error of first level parameter identification is 2.196 8%, and the result is converged within 40 iterations; the relative residual error of the second level is 0.840 3%, and the result is converged within 20 iterations. It is concluded that the method that two levels of parameter identification of MF tire model based on genetic algorithm can ensure the parameter identification accuracy and improve identification efficiency, which provides an efficient and reliable method for real-time parameter identification.

vehicle engineering; tire model; magic formula; genetic algorithm; parameter identification

10.3969/j.issn.1674-0696.2017.05.20

2016-03-12；

2016-11-12

国家自然科学基金项目(51175269)

边 伟(1967—)，女，河南商丘人，副教授，主要从事汽车机电一体化技术与运用方面的研究。E-mail：b3415417@126.com。

龚佳慧(1991—)，女，江苏扬州人，硕士，主要从事车辆电子控制技术应用方面的研究。E-mail：15195955668@163.com。

U463.341

A

1674- 0696(2017)05-115- 06