单箱双室薄壁混凝土连续箱梁剪力滞效应分析

陈 印, 唐怀平

(西南交通大学， 四川成都 610031)



单箱双室薄壁混凝土连续箱梁剪力滞效应分析

陈 印, 唐怀平

(西南交通大学， 四川成都 610031)

混凝箱梁具有抗弯刚度大、稳定性高和适应现代化施工等特点，广泛应用于简支梁桥、连续梁桥、拱桥和混凝土斜拉桥等桥梁常用的主梁结构形式。文章针对翼板沿横向变化的单箱双室薄壁混凝土连续箱梁，利用有限元模拟箱梁在不同集中力和均布荷载作用下，箱梁剪力滞的分布规律。

连续箱梁； 单箱双室； 有限元； 剪力滞

初等梁理论认为，在不考虑剪切应变对纵向变形影响的情况下，当某对称荷载作用于箱梁的两肋板时，翼板的正应力与其到中性轴的距离成正比，且正应力在顶板与底板横向各处都相等。

实际的带翼缘板的T梁和箱形截面梁，在对称垂直力作用下，翼缘板上的正应力沿宽度方向呈不均匀的分布状态。这种由于腹板处剪力流向翼缘板中传递的滞后而导致翼缘板正应力沿宽度方向呈不均匀分布的现象，称为“剪力滞效应”。如果靠近腹板处翼缘板中的正应力大于初等梁理论的正应力，称为“正剪力滞效应”，反之称为“负剪力滞效应”。在宽翼缘梁的设计分析中，如果忽略剪力滞效应，将低估结构的实际应力大小，使其应力分布状态与实际不符，从而可能造成梁体开裂、跨中超限下挠等安全和耐久性问题[1]。

在工程中在工程当中，目前较为常用的方法是引入剪力滞系数λ的概念，研究人员可根据λ值的大小以及其分布情况能够方便直观地描述箱梁截面的正负剪力滞效应，以及剪力滞效应的强弱程度[2]。

式中：σ(x,y,z)为考虑剪力变形求得的法向应力；σ0(x,z)为按初等梁理论求得的法向应力。

1 箱梁剪力滞效应微分方程

1.1 三杆比拟法的等效处理[3]

对称箱梁在竖向荷载作用下，原来由翼板和腹板共同承担的内力，现在模型简化为一个附加的等效面积计入翼板，等效翼板进一步简化为承受荷载的三个比拟杆和传递剪力的等效薄板(图1)。

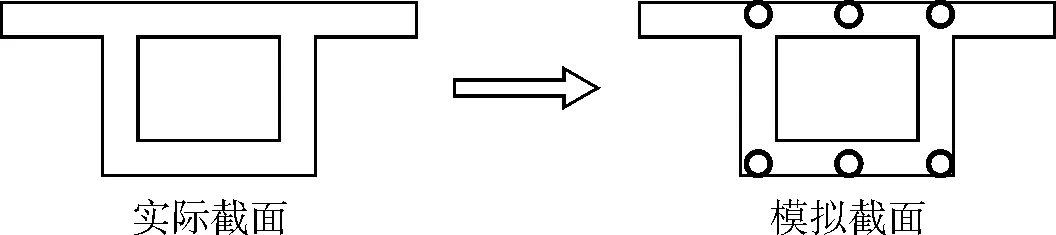
图1 箱梁三杆比拟法示意

1.2 三杆比拟法微分方程

假设作用在箱梁任意截面上的竖向剪力Q(x)完全由腹板承受，且均匀分布在腹板上。于是作用的剪力流可以近似为

式中：2表示两个腹板，h表示顶板中点到底板中点的高度。根据力平衡和变形协调条件，对于边杆：

对于边杆：

式中：qE(x)为由于外荷载引起的剪力流；q为薄板传递的未知剪力流；FE为截面处由腹板传递给翼板的剪力；FC为薄板传递的剪力。利用剪切角的增量原理并将上式代入，剪力流的平衡方程为

其全解为：

q=C1shkx+C2chkx+R/(A1k2)qE(x)

式中：R、k是与翼板几何参数有关的常数[4]。

上式表明，剪力流与翼板参数、截面位置及外荷载有关。

2 连续箱梁剪力滞效应有限元分析

2.1 桥梁概况

某连续箱梁，翼板沿横向均匀变化，设计为单箱双室混凝土直梁，单跨跨度为40 m，双向八车道，箱梁顶面宽17.5 m，立面高2.2 m，C50混凝土，分左右两幅，两幅之间设置中央隔离带。桥的立面见图2，横截面见图3。

图2 联系梁立面(单位:mm)

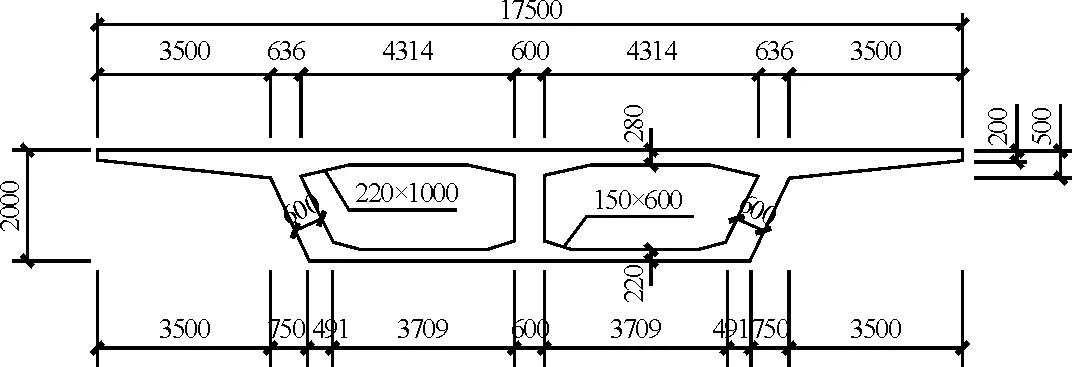
图3 箱梁横截面(单位：mm)

2.2 连续梁的有限元分析

采用大型有限元ANSYS 14.5建立桥梁模型见图4。

图4 有限元建模

材料基本参数为：

弹性模量：E=3.45×104MPa； 密度：ρ=2 600 kg/m3； 泊松比：μ=0.3； 单元类型：solid95。

2.3 集中力作用下双箱室连续梁剪力滞研究

分析中集中力采用P=400 kN。荷载工况如图5所示，为避免集中力作用下产生应力集中现象，加载时荷载平均分配到周围几个节点。

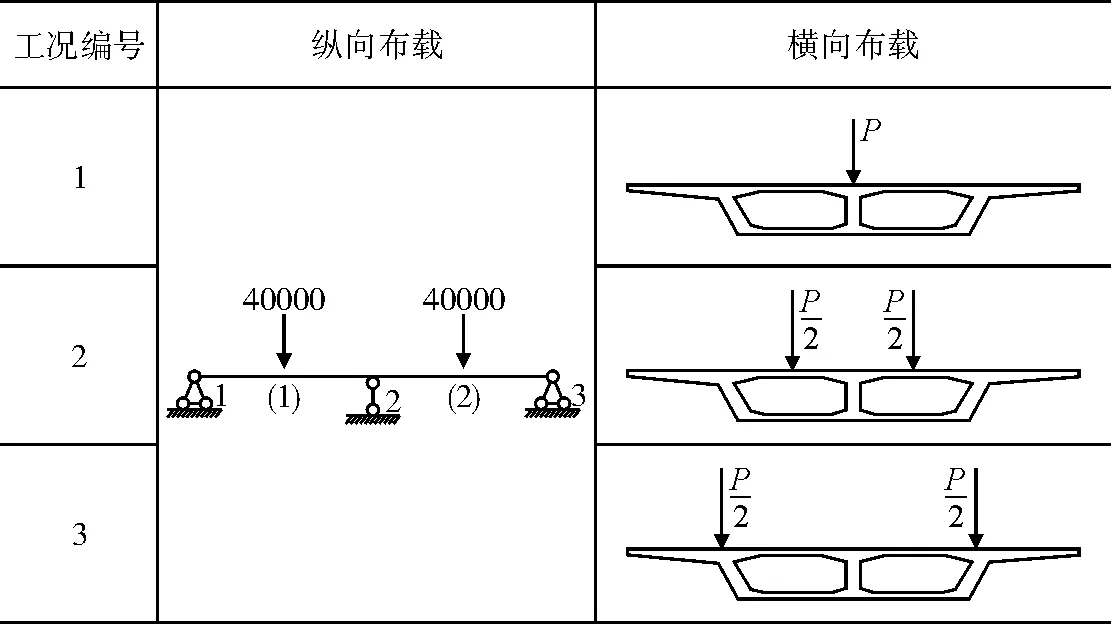
图5 集中力加载

箱梁顶、底板跨中剪力滞系数如图6、图7所示。

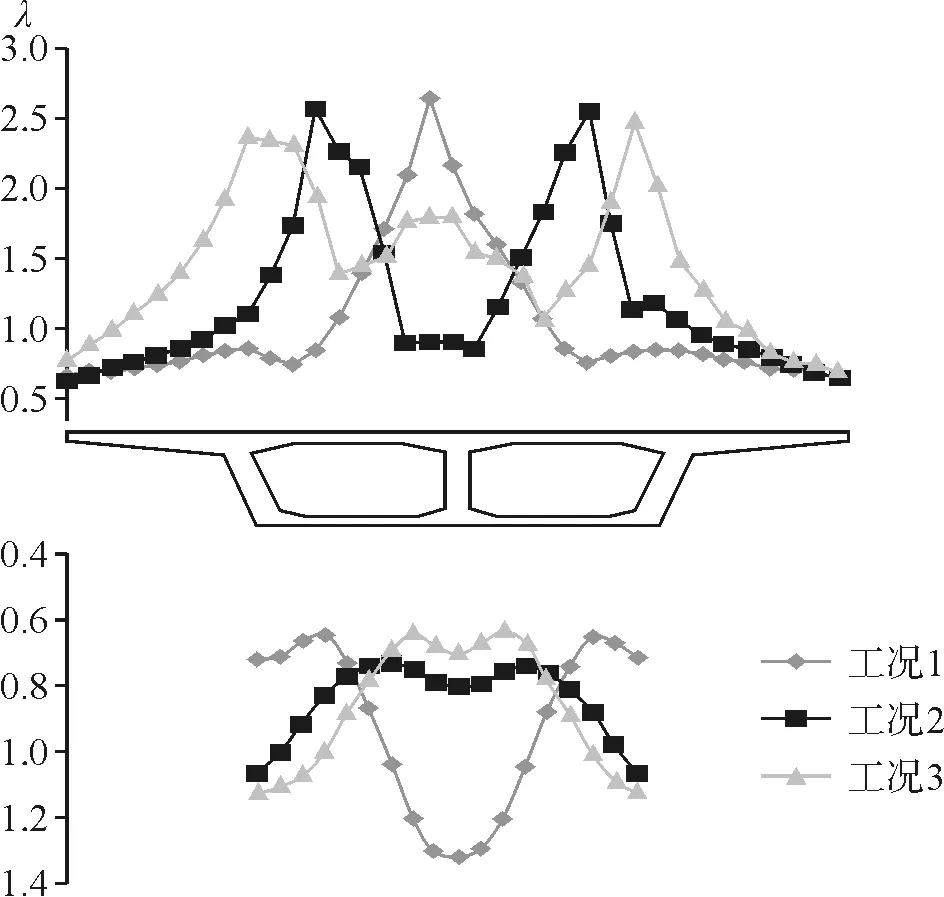
图6 工况1～工况3断面一剪力滞系数

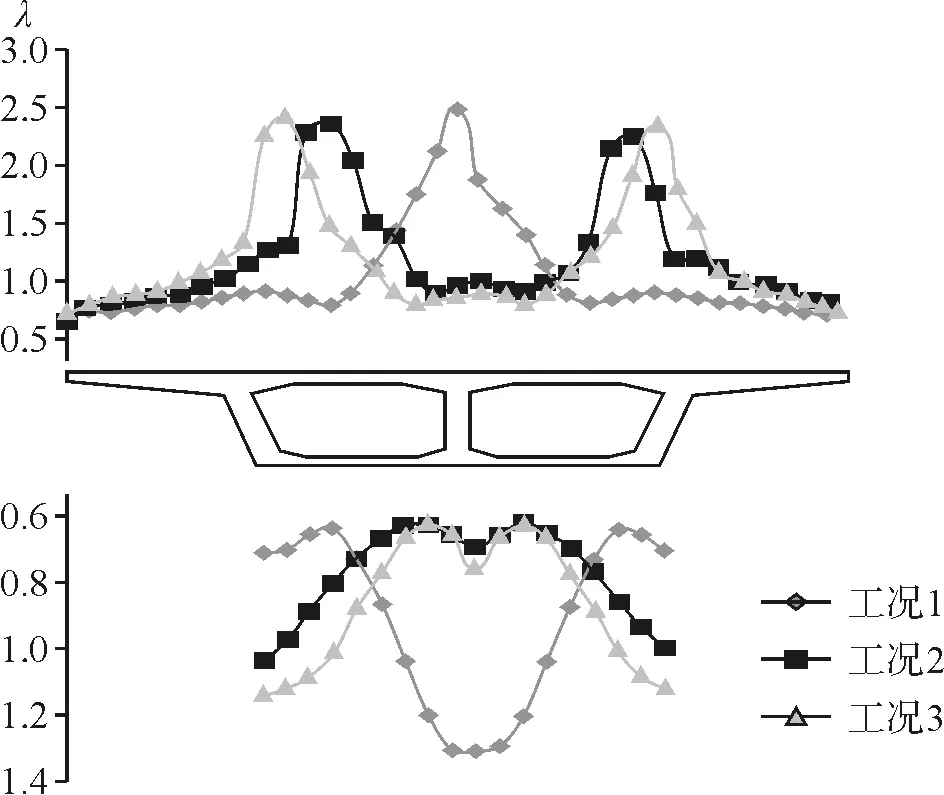
图7 工况1～工况3断面二剪力滞系数

由图6、图7可以看出，在工况1、工况2和工况3作用下，双箱室连续梁跨中顶、底板整体大致出现正剪力滞效应，且由于荷载是对称作用，剪力滞效应基本对称。当集中力作用在中心腹板处时(工况1)，剪力滞系数在中心腹板处达到峰值，峰值为2.6，并以中心腹板处往两边递减。当集中力平均作用在两边腹板处时(工况3)，剪力滞系数在三个腹板处都存在峰值，并向两侧递减。三种工况下，箱梁底板剪力滞系数比顶板剪力滞系数小。由上述三种工况可知，剪力滞与集中力的作用点相关。

2.4 均布荷载与集中力共同作用下双箱室连续梁剪力滞研究

集中力采用P=400 kN，均布荷载采用q=160 kN/m[5]，荷载工况如图8。同样，为避免集中力作用下产生应力集中现象，加载集中力时荷载平均分配到周围几个节点。

图8 均布荷载与集中力共同加载

箱梁顶、底板跨中断面剪力滞系数如图9、图10所示，由于结构和荷载都是对称的，剪力滞系数也基本对称。

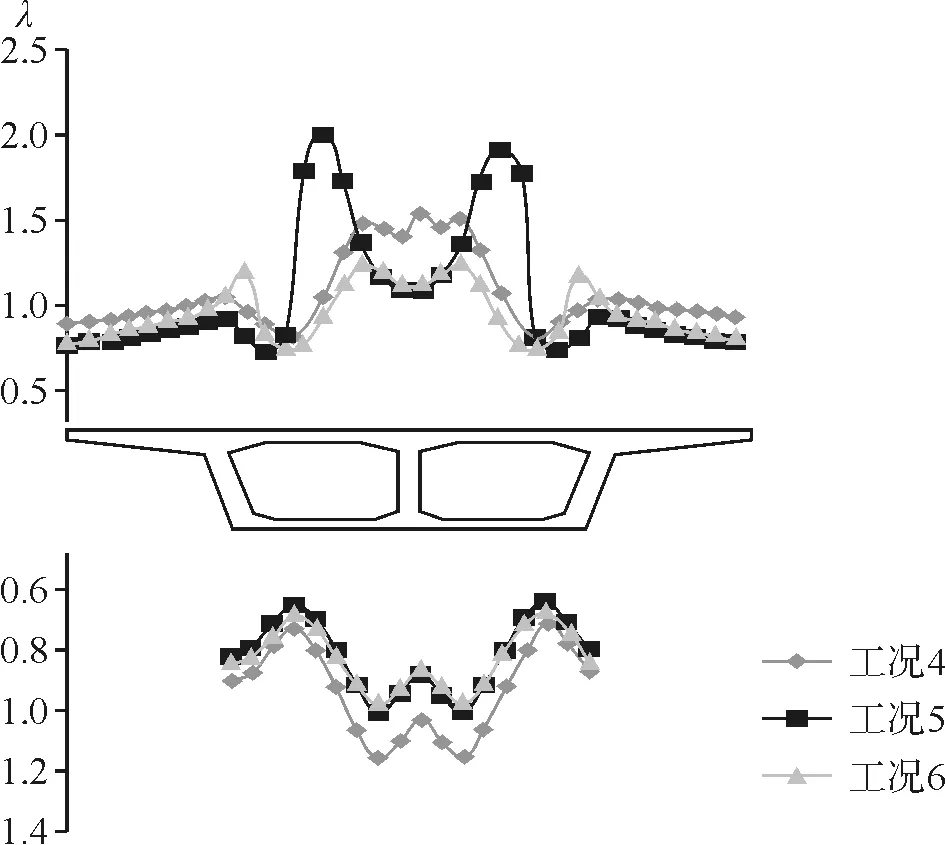
图9 工况4～工况6断面一剪力滞系数

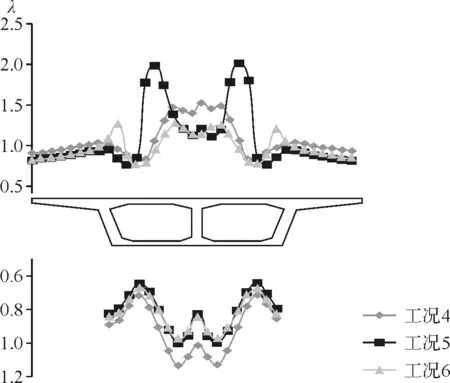
图10 工况4～工况6断面二剪力滞系数

均布荷载与集中力共同作用下与剪力滞效应与集中力单独作用下的分布趋势基本相同，但是剪力滞系数较后者小，且剪力滞分布差异较集中力单独作用下相对较小。剪力滞系数最大值出现在工况5作用下，峰值为1.99。箱梁在工况4、工况5、工况6作用下，翼板剪力滞系数走向与数值都基本相同。

3 结论

(1)三杆比拟法模拟表明：剪力流与翼板参数、截面位置及外荷载有关。

(2)以单箱双室薄壁箱梁为代表的多箱室箱梁，集中力作用点不同，剪力滞效应不尽相同，且集中力单独作用在中心腹板处时，剪力滞系数最大达到2.6，这在以后的设计中应考虑作用力作用在不同点时对箱梁产生的不同影响。

(3)均布荷载与集中力共同作用载多箱室箱梁，较集中力单独作用下的分布趋势基本相同，但是剪力滞系数较后者小，且剪力滞系数分布差异也较后者小。

[1] 孙璐,王文雷,吴国琦,等.客运专线箱梁端部裂纹成因分析及施工控制[J].铁道工程学报,2007(10)：46-51.

[2] Evans H R. Taherian A R. The prediction of the shear lag effect in box girder[J].Proc.Instn.Civ.Engrs,Part 2,1997,(63):69-72.

[3] 唐怀平,唐达培.大跨径连续刚构箱梁剪力滞效应分析[J].西南交通大学学报，2001(6)：617-619.

[4] 张士铎.变高度梯形单箱室箱梁畸变计算[J].土木工程学报，1987(4)：30-34.

[5] 蔺鹏臻, 孙理想, 杨子江, 等.单箱双室简支箱梁的剪力滞效应研究[J]. 铁道工程学报,2014(1):59-63.

陈印(1988～)，男，硕士研究生，研究方向为工程力学桥梁。

TU312+.1

A

[定稿日期]2016-12-26