基于Duhamel积分的地震作用下车桥耦合振动分析

谢智奕， 沈火明

(西南交通大学力学与工程学院，四川成都 610031)



基于Duhamel积分的地震作用下车桥耦合振动分析

谢智奕， 沈火明

(西南交通大学力学与工程学院，四川成都 610031)

文章应用达朗贝尔原理推导了6自由度车辆模型，应用有限元法推导了桥梁模型，应用逆迭代法求解两个系统的模态振型和自振频率，采用加速度输入模式将地震输入到车桥耦合系统中，最后通过Duhamel积分法和振型叠加法求得车桥耦合系统的动力响应，通过算例与传统Newmark-β法相对比，结果表明：通过本文方法计算的地震作用下车桥耦合的动力响应结果与传统Newmark-β法的结果接近，极值点误差范围在5 %以内。

车桥耦合； 地震作用； Duhamel积分； Newmark-β法； 振型叠加法

随着高速铁路的大量普及，客运列车向着高速化、货运列车向着重载化的方向发展，车桥耦合问题已经成为国内外学者研究的热点[1-6]。而地震作用会对桥梁造成严重破坏，极大地影响桥梁上车辆行驶的安全，因此对地震作用下的车桥耦合问题研究具有重要意义。地震波在地面的运动是一种复杂的空间运动，地震加速度不仅包括水平向分量，还包括竖向分量。根据大量资料及研究[1-5]、[10]，虽然水平作用对桥梁结构的影响最大，但是当车辆行驶在桥梁上时，地震的竖向作用对车辆行驶危害也非常大，甚至会造成脱轨危险，极大地威胁着车辆及乘客的安全，所以本文主要研究地震的竖向作用。目前研究地震作用下的车桥耦合问题通常采用的是Newmark积分法等逐步积分法，但是该方法对时间精度的要求较高，而一些地震波的记录由于持时较长，所取时间间隔也相对较长，这就影响了计算的精确度。本文采用基于Duhamel积分的车桥耦合动力分析方法，该方法能显著提高积分步长[6]，从而解决了地震波记录数据时间间隔的问题。

1 Duhamel积分法[6]

设一低阻尼单自由度系统的运动方程为

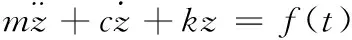
(1)

其中m、k、c是系统的质量、刚度和阻尼，z为位移，f(t)为荷载力。整理得到：

(2)

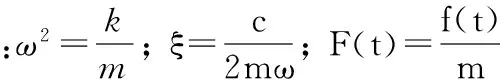
将式(2)的解用Duhamel积分展开并整理得到：

(3)

求导得到：

(4)

式中：

(5)

(6)

(7)

(8)

(9)

这里假设荷载在(t, t+Δt)内是线性变化的，有

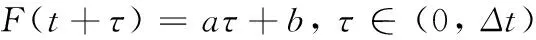
(10)

通过式(10)可以确定参数a，b的值。对于某确定结构，其ω、ξ为定值，在Δt不变的情况下，计算中的H、Q和P也保持不变，根据式(3)和式(4)将上一时刻的动力响应带入计算可得下一时刻的动力响应，在整个时间段内依次积分最后得全时间段的动力响应。

2 车桥耦合模型

2.1 桥梁模型

桥梁系统包括主梁、桥墩和支座，本文在计算时不考虑支座和墩高对车桥耦合的影响，故设桥墩与主梁刚结，桥墩与主梁参数一致。采用平面刚架单元建立桥梁有限元模型，其位移向量为[ui,vi,θi,uj,vj,θj]T，单元内部点的位移计算采用Hermite插值[7]计算，质量矩阵采用一致质量矩阵，其单位质量矩阵为：

(11)

桥梁阻尼采用Rayleigh阻尼，

CB=a0MB+a1KB

(12)

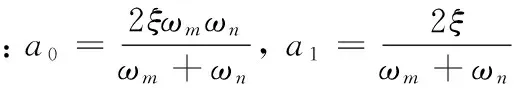
ωm、ωn为桥梁系统前两阶自振频率，MB、KB分别为桥梁的质量矩阵和刚度矩阵。

2.2 车辆模型

车辆系统采用刚体-弹簧-阻尼的整车模型，由于沿车辆运行方向的纵向振动对桥梁的竖向振动影响极小，并且车辆竖向与横向振动之间的耦合效应较弱，因此本文在计算时将车桥耦合振动响应分为竖向与横向两个平面振动，所以在车桥耦合振动分析中，仅分析车辆的浮沉与点头2个自由度，包括车体及前后转向架共6个自由度。假设两转向架的一、二系弹簧刚度、阻尼系数相同，采用达朗贝尔原理推导其质量矩阵、刚度矩阵和阻尼矩阵，得到车辆系统的运动方程[1]。

2.3 车桥耦合模型

桥梁与车辆系统的运动方程为：

(13)

(14)

式中下标B、V分别代表桥梁系统和车辆系统，FBV和FVB为车辆与桥梁的相互作用力。

两个系统通过轮轨接触相联系，本文不考虑轨道不平顺的影响，对两个系统采用振型叠加法，将其运动方程化为模态运动方程[6]。

对于桥梁系统，设其为正交阻尼结构，采用逆迭代法求解系统的振型ΦB和自振频率ωB，假设各阶模态阻尼比为ξB，设桥梁的广义振型坐标列向量为qB，则位移向量可表示为：

(15)

将式(15)代入式(13)中，可以得到桥梁系统的模态运动方程：

(16)

对于车辆系统，由于其阻尼矩阵CV不具有正交性，因此引入假定的车辆阻尼比ξV，并将式(14)中的阻尼相移动到右端，再进行同样的模态变换，可以得到车辆系统的模态运动方程：

(17)

3 地震激励的输入

地震激励的输入采用加速度输入模式[8]，直接运用实测地震波的加速度时程，不考虑行波效应，广义地震力[5]为：

(18)

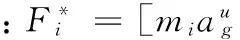
4 算例

选取单节四轴列车在地震作用下通过一32 m的简支梁桥作为算例，地震波选取典型强震记录El-Centro波输入，采用纵向+竖向一致输入，竖向地震加速度时程与纵向一致，但加速度峰值取0.65倍。不考虑轨道不平顺，车速v取50 m/s，车辆信息见文献[9]。桥梁弹性模量E取35 GPa，横截面积A为4.8 m2，截面抗弯惯性矩I取22 m4，密度取2 600 kg/ m3，桥梁划分为长度一致的320个梁单元，取前20阶模态，各阶模态阻尼比取为0.05。当地震开始时列车上桥，地震持时50 s，步长取与地震波记录时间间隔一致为0.02 s。为验证本方法的正确性，将本文方法与传统Newmark-β法的结果作对比，计算结果如图1和图2所示。

图1 Newmark-β法计算的桥梁跨中竖向加速度时程

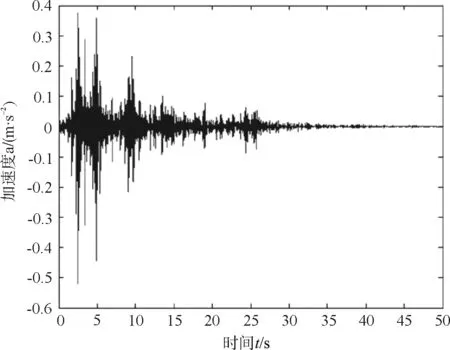
图2 本文方法计算的跨中加速度时程

从图1和图2可见，本文的方法和传统Newmark-β法求得的地震作用下车桥耦合动力响应结果非常接近，极值点的误差范围在5 %以内，说明本文的方法可行。

5 结束语

应用达朗贝尔原理推导了6自由度车辆模型，应用有限元法推导了桥梁模型，应用逆迭代法求解两个系统的模态振型和自振频率，采用加速度输入模式将地震输入到车桥耦合系统中，最后通过Duhamel积分法和振型叠加法求得车桥耦合系统的动力响应，并与传统Newmark-β法相对比，验证了本文方法的可行性。

[1] XIA H，DEROECKG，GOICOLEAJ M.Bridgevibration and controls: newresearch [M].New York:Nova Science Publishers Inc.，2011:15 -65.

[2] 翟婉明.车辆-轨道耦合动力学[M]. 北京:科学出版社，2007:1-11，116-133.

[3] 翟婉明，夏禾. 列车-轨道-桥梁动力相互作用理论与工程应用[M]. 北京:科学出版社，2011 : 8-23.

[4] 杜宪亭. 强地震作用下大跨度桥梁空间动力效应及列车运行安全研究[D]. 北京:北京交通大学，2011.

[5] 夏禾. 车辆与结构动力相互作用[M]. 北京:科学出版社，2002 : 11 -29，88 -92,200-207.

[6] 乔宏，夏禾，杜宪亭. 基于Duhamel积分的车桥耦合动力分析方法[J]. 西南交通大学学报，2014，49(5): 766-771.

[7] 余华，吴定俊. Hermite插值在车桥祸合振动中的应用[J]. 振动与冲击， 2006，25(2): 38-40.

[8] 董延龙. 地震作用下高铁的车桥耦合振动分析[D]. 武汉: 华中科技大学，2013: 16-18.

[9] 杜宪亭，夏禾，张田，等. 基于精细Runge-Kutta混合积分法的车桥耦合振动非迭代求解算法[J]. 振动与冲击，2013，32(13): 39-42.

[10] 贾志明，高大峰. 基于大质量法地震竖向作用下连续刚构桥地震响应分析[J]. 四川建筑, 2011，31(1): 140-141.

谢智奕(1991～)，男，硕士研究生，研究方向为噪声与振动控制。

沈火明(1968～)，男，博士，教授，博士生导师，研究方向为结构振动与控制。

U441+.3

A

[定稿日期]2017-03-25