双层隔振装置的Matlab辅助设计与实验验证
李旭巍, 高芳清, 姜文恺
(西南交通大学力学与工程学院, 四川成都 610031)
双层隔振装置的Matlab辅助设计与实验验证
李旭巍, 高芳清, 姜文恺
(西南交通大学力学与工程学院, 四川成都 610031)
文章通过对双层隔振系统力传递率的理论推导,给出了确定系统隔振效果的可变设计参数。基于系统振动控制微分方程及其求解算式,利用MATLAB图形用户界面设计(GUI)优势,开发出双层隔振系统的可视化辅助设计程式与界面,仅以主要参数的试选与输入即可得到系统的力传递曲线,便于指导普通技术人员的工程设计,以达到理想的隔振效果。为此还通过一款实型装置的开发给出了其设计程式和室内实验验证。
双层隔振系统; 力传递率; MATLAB; 隔振实验
1 引言
工程上、生活中很多振动源会引起多大或超标的环境振动和噪声问题,对振源进行主动隔振是常规而广泛使用的振动控制方法之一。隔振措施能够有效阻隔激励源能量流的传递,抑制结构振动向外传播,从而降低或减少结构声的产生。大量应用和实验表明,单层隔振装置主要对低频振动隔离有效,而对于中高频振动的隔离效果不理想。为提高中高频振动的隔振效果,国外自从60年代开始采用双层隔振[1]。
所谓双层隔振系统就是在被隔离的机械设备和基础之间再插入一个弹性支承着的中间质量,整个双层隔振装置由机器、中间质量块、基座和两层隔振器组成,双层隔振系统可以简化为如图1所示的两自由度系统[2]。与单层隔振系统相比,双层隔振系统能更好的抑制机械振动能量传递,能更好的隔离到基础的高频振动,因而具有明显的优越性,使用更广泛[3]。
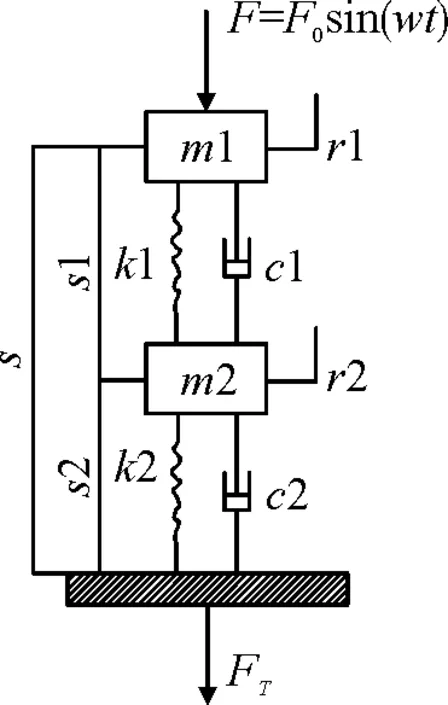
图1 双层隔振力学模型
1 双层隔振装置动力特性分析
1.1 力传递率公式的推导
对于图1所示的双层隔振,其固有频率方程式为:
(1)
输入为作用到机械设备上的扰动力F(t)=F0sin(wt)。
输出为:
(1)传递力FT;
(2)m1及m2的绝对位移x1、x2;
(3)m1和m2之间的相对位移δ1。
图1中:m1为被隔振物体质量;m2为中间质量块质量;k1、c1分别为上层隔振器刚度和阻尼;k2、k2分别为下层隔振器的刚度和阻尼;FT为传递到基础的力。
运动微分方程为:
m1x1+k1(x1-x2)+c1(x1-x2)=F0sin(wt)
m2x2-k1(x1-x2)-c1(x1-x2)+k2x2+c2x2=0
改为矩阵形式:
(2)
其中:F(t)=F0Imejwtj2=-1
设:
(3)
则:H1(w)为输入力F(t)和被隔振对象的位移x1之间的频响函数;H2(w)为输入力F(t)和位移x2之间的频响函数;H3(w)为输入力F(t)和δ1之间的频响函数;H4(w)为输入力F(t)和传递至基础上的力FT之间的频响函数。
将式(2)经过拉普拉斯变化,并将s=jw带入,有:
(4)
按矩阵运算法则,式(3)可改写为:
(5)
记式(4)为:
(6)
式中|z|=(k1-m1w2+jc1w)[k1+k2-m2w2+jw(c1+c2)]-(k1+jc1w)2=m1m2w4-(m2k1+m1k2+m1k1+c1c2)w2+k1k2-jw3(m2c1+m1c1+m1c2)+jw(c1k2+c2k1)=Δ显然,当不计阻尼时,式Δ即为频率方程式(1)
由式(6)可得:
(7)
(8)
因为δ1(t)=x1(t)-x2(t)=H1(w)·F(t)-H2(w)·F(t),所以
(9)
因为FT(t)=k2·x2(t)+c2·x2(t)=(k2+jwc2)H2(w)·F(t),所以
(10)
设:
并对式(7)-式(10)右边分子分母同时除以m1m2w4,则可得到用无因次量纲表示的频响函数,如果令:
则:
这里,可得双层隔振系统的绝对传递率:
(11)

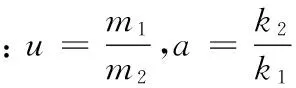
1.2 双层隔振装置力传递率曲线的编程设计
一般而言,常用分贝的形式表达传递率函数,即
对使用MATLAB来分析数据、求解问题、绘制结果的大多数人来说,GUI(图形用户界面设计)对他们而言是不太重要的,但是,如果编程者要向别人提供应用程序,那么用户界面的友好性几乎和程序功能同样重要。最常见的控制和激活方式是用鼠标来控制频幕上的鼠标的运动,按下鼠标按钮,标志着对象的选择或其他动作[5]。基于MATLAB的GUI设计的这些优点,下面,就用MATLAB的GUI来编程设计画双层隔振力传递率的曲线。
为方便利用MATLAB语言进行编程计算求解,首先对式(11)进行处理,
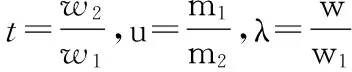
这里,选用MATLABGUI布局编辑器里面的控件图标:PushButton、EditText、StaticText、Axes,采用6个EditText和6个StaticText,分别表示输入的参数数值和名称,采用两个PushButton来表示绘图和获得双层隔振示意图,采用两个Axes来显示所需图片和曲线。具体用途如图2所示。

图2 MATLAB编程

通过这个MATLAB用户界面,我们只需要在图2中输入被隔振物体m1、中间质量块m2、上层隔振器刚度k1、下层隔振器刚度k2、上层隔振器阻尼ξ1和下层隔振器阻尼ξ2的数值,就可以快速的得出相应的力传递率曲线,从而可以达到分析双层隔振系统的隔振效果。该GUI界面设计适合于任何双层隔振系统,应用相当广泛便捷。
2 某型双层隔振装置的参数选配与实验验证
2.1 以某地区室内配电房使用的干式变压器为对象进行实际应用
2.1.1 装置的应用及设计开发
针对某楼内配电房变压器所致环境振动治理,专门开发出一款双层隔振装置,以期有效降低环境振动和噪声的影响。经实地考察与量测,该变压器为10 kV级SCB10-800型干式变压器,变压器底座的尺寸长与宽均取820 mm,变压器运行时振动辐射主要是以100 Hz及其倍频程为主[8]。
(1)确定振源质量。
基于10 kV级SCB10-800型干式变压器类型,可查阅得到该类变压器质量在2 200~2 800 kg之间,这里为了方便,取整数质量为3 000 kg。
(2)确定中间质量块。
理论上认为,双层隔振中间质量越大,则双层隔振就能够获得更好的效果。然而,结构中增加这样一个庞大而无实际用途的部分往往十分昂贵甚至有时候根本不可行,尤其是如果无法为中间质量分配一块连续和足够的安装空间[9]。以额定容量为800 kvA的干式变压器为例,在有外防护罩时,其上部空间的高度集中在20~30 cm的范围内,若隔振器的高度取为10 cm,则中间质量块的高度应控制在20 cm内,同时,为了保证安装,装置的长宽应该大于对象安装尺寸,所以,综上所述,中间质量块的尺寸也是有尺寸限制的。以被隔振对象为例,安装尺寸为820×820 mm,上部空间约300 mm,可以初步拟定中间质量块的长宽高为900 mm、900 mm和100 mm,如果选用钢材,取钢材密度为7.85 t/m3,则中间质量块的质量m2=635.85 kg,质量比u=3.45~4.40。这里,一般取中间质量块的质量为变压器的10 %~20 %,即u=5-10。
(3)确定刚度比及减振装置的阻尼比。
关于上层和下层隔振器的刚度之比,建议取值范围为0.8×(1+1/u)~1.2×(1+1/u)[10]。以上海青浦环新减震器厂生产的产品为例,具体数值见表1。

表1 上层和下层隔振器的刚度比
注:额定荷载表示隔振器的最佳使用荷载,其荷载范围可取额定荷载±20%。
可以选出:上层隔振器采用ZD型,下层隔振器采用ZDE型,上下层都采用6点布置。设计出来的双层隔振装置见图3。

图3 双层隔振装置
(4)双层隔振装置的实验。
对设计的双层隔振装置在实验室进行测量,采用混凝土块模拟变压器,依次取混凝土块质量m1为1 000 kg、1 500 kg和2 000 kg;采用激振器对被隔振物体进行激振模拟变压器振动,分别在第一层和第二层上面布置加速度传感器,在激振器激振杆端部布置力传感器。然后基于实验室已有的振动设备进行测量、分析(图4)。

图4 双层隔振装置实验示意

(12)
在MATLABGUI图形界面里面分别代入输入m1、m2、k1、k2、ξ1、ξ2把这6个参数分别代入可视化界面,分别得出3条力传递率曲线(图5)。

图5 不同质量比的力传递率曲线
TA1表示当质量比u=5时的力传递率曲线,TA2表示当质量比u=7.5时的力传递率曲线,TA3表示当质量比u=10时的力传递率曲线。将激励频率为100 Hz、200 Hz、300 Hz和400 Hz时,对应的平均加速度值见表2。
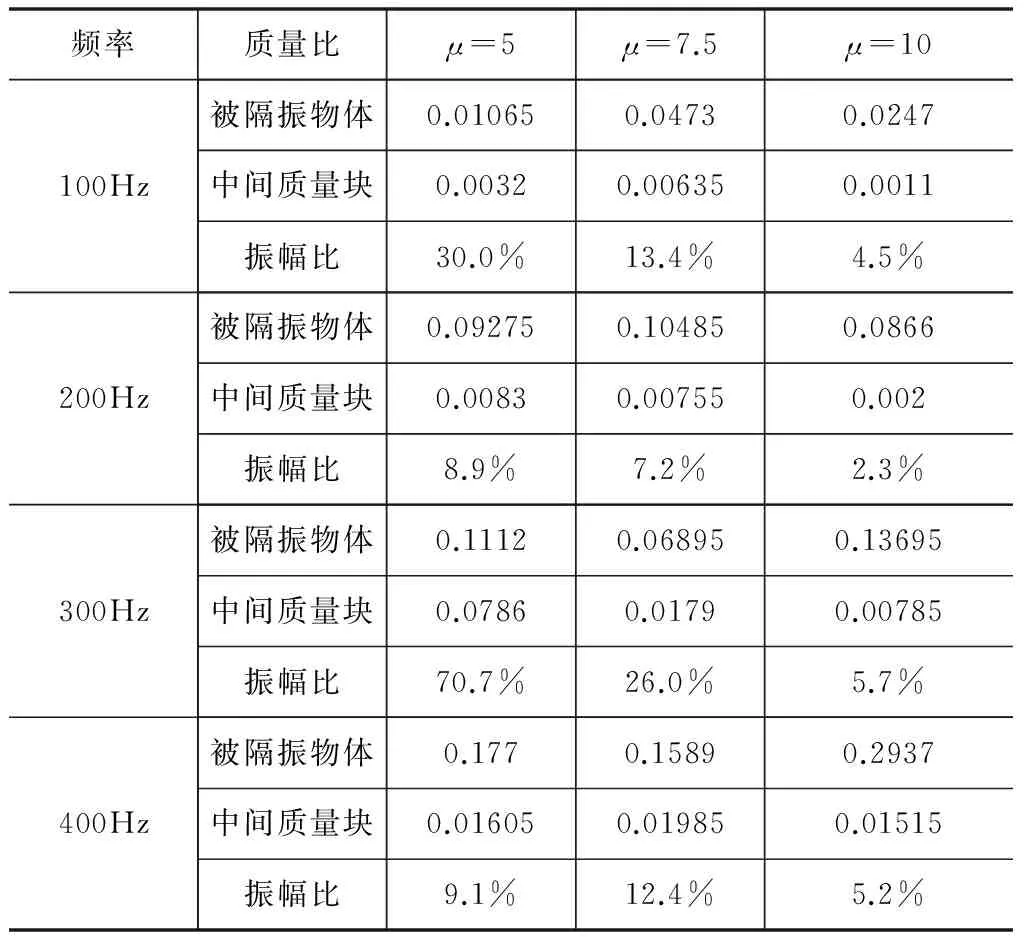
表2 在不同频率下隔振装置振动衰减规律
注:加速度g取9.8 m/s2。
对表中数据进行处理,可以得到图6。
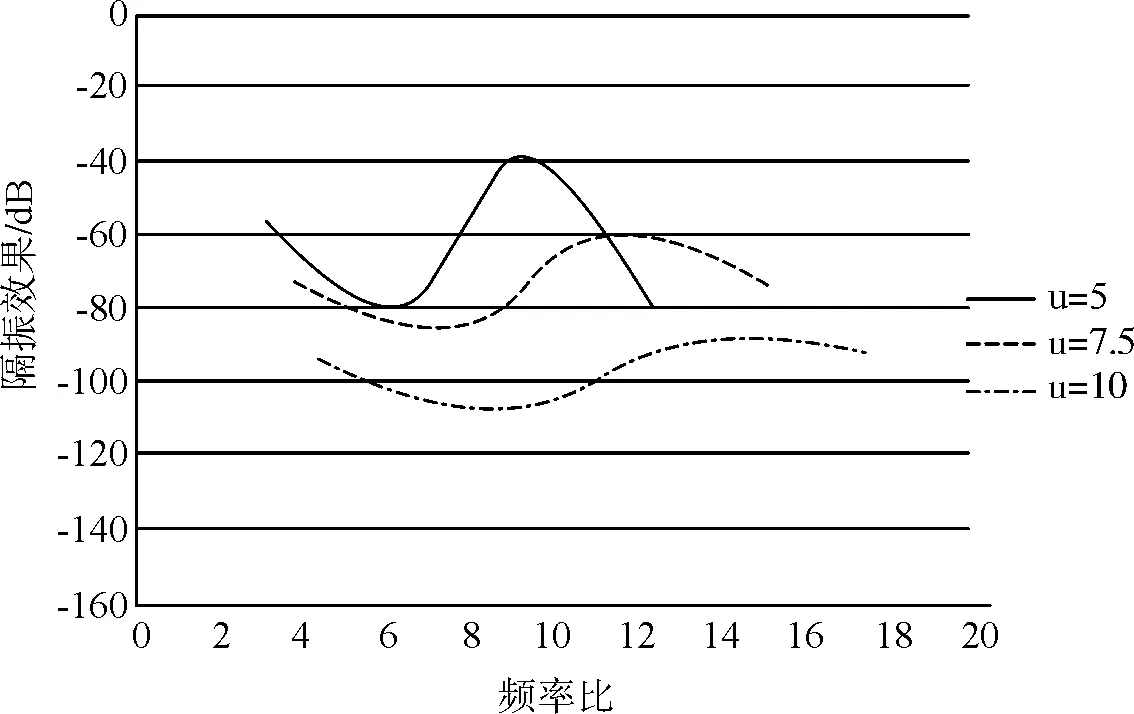
图6 隔振效果实测
把图5和图6结合起来分析,可以得到对比图7。可以看出,实测结果与预测结果出现了较大的偏差,说明在实际工程中,影响隔振效果的因素还有很多,比如基础的非刚性,被隔振设备的非刚性等。因此,有必要对理论推导的力传递率公式进行处理,把结果乘上一个隔振效果折减系数ɑ,取值范围在0.6~0.8之间,这样,处理过后效果就很明显了(图8)。
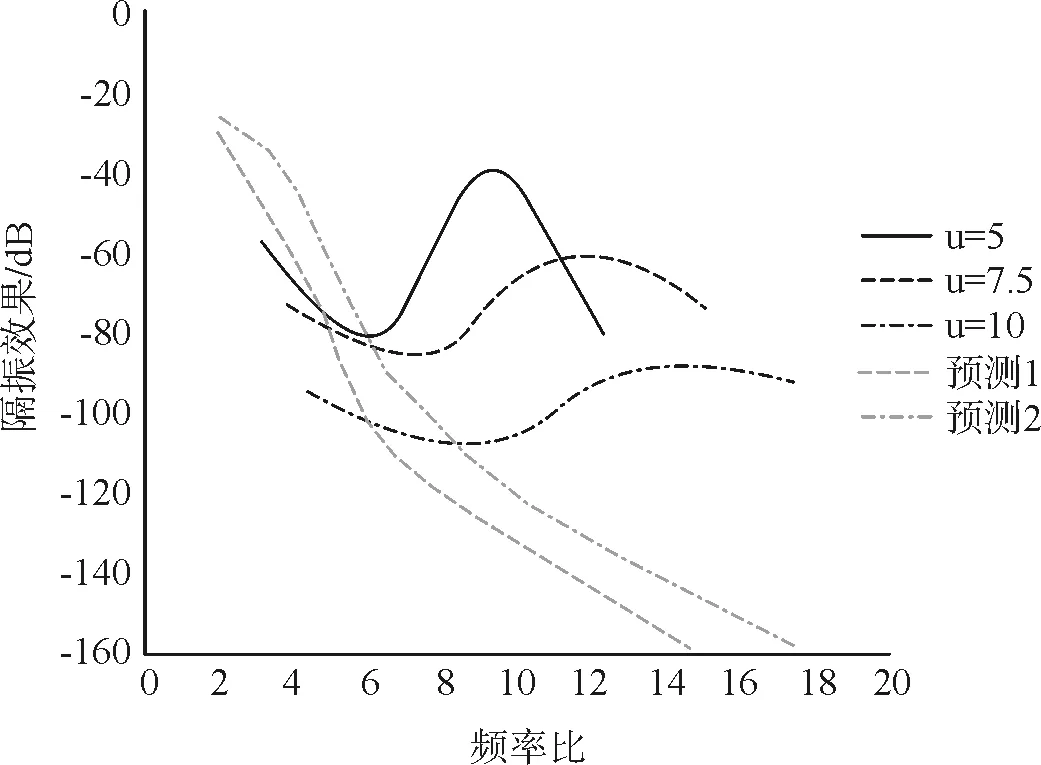
图7 实测和预测结果

图8 隔振效果预测
4 结论
(1)通过对双层隔振系统力传递率的理论推导,给出了评价隔振效果的参考公式,能够清楚的看出影响隔振效果的几个参数。
(2)巧妙运用MATLAB的计算可视化特点,将杂乱的数据通过图形来表示从中观察出其内在的关系,设计出图形用户界面,方便地进行人机交互。针对不同的隔振对象,采用双层隔振系统进行减振设计分析,选择合适的参数,从而达到理想的效果。
(3)对一款实型装置的开发设计,在室内进行了实验验 证,证明了运用MATLAB辅助设计双层隔振装置的优越性。
本文的研究具有一定的参考价值,有着良好的推广应用前景。
[1] 严济宽.机械振动隔离技术[M].上海:上海科学技术文献出版社,1985.
[2] 张满满.船用辅机浮筏隔振系统的静态及动态特性研究[D].武汉:华中科技大学,2002.
[3] 沈荣瀛,卢峥.MTU柴油发电机组隔振装置振动固有特性分析[J].噪声与振动控制,1994(3): 2-7.
[4] 向敢.浮筏隔振系统的振动特性研究[D].杭州:浙江工业大学,2012.
[5] 梅志红,杨万铨.MATLAB程序设计基础及其应用[M].北京:清华大学出版社,2005.
[6] 朱石坚,楼京俊,何其伟.振动理论与隔振技术[M].北京:国防工业出版社,2008.
[7] 吴琪.室内配变电设施双层隔振设计研究[D].成都:西南交通大学,2016.
[8] 洪陈玉.小区变压器环境振动传播与隔振研究[D].成都:西南交通大学,2012.
[9] 杜冬.多个中间质量隔振最优设计及其性能研究[D].上海:上海交通大学,2007.
[10] 成大先.机械设计手册[M]. 4版. 北京:化学工业出版社,2004.
[11] Stephen J.Chapman.MATLAB Programming for Engineers[M].北京:科学出版社,2003.
[12] J.T.Broch.Mechanical Vibration and Shock Measurements.B&K,1984.
李旭巍(1990~),男,硕士研究生,主要从事结构振动与控制方研究。
TU352.12
A
[定稿日期]2017-03-16

