非单色性光源对杨氏干涉条纹可见度的影响*

张 燕 翟 影 候云浪 祝 昆

(六盘水师范学院物理与电子科学系 贵州 六盘水 553004)

非单色性光源对杨氏干涉条纹可见度的影响*

张 燕 翟 影 候云浪 祝 昆

(六盘水师范学院物理与电子科学系 贵州 六盘水 553004)

光源的单色性影响其相干性．任何实际的波列都有一定的谱线宽度，谱线宽度表示了光源单色性的好坏，直接影响了干涉条纹的可见度．对非单色性光源通过典型杨氏双缝干涉装置产生干涉条纹的理论进行分析和仿真，得出谱线宽度与干涉条纹的可见度的关系．结论与实验相吻合．其结果对于干涉法工程测量具有现实意义．

干涉条纹 可见度 非单色性光源

1 引言

相干性是光源的一种重要特性，由干涉条纹的可见程度综合表现出来．单一波长的波列只是一种理想情况，任何实际的波列都有一定谱线宽度．谱线中心对应中心波长，谱线宽度表示了光源单色性的好坏，谱线宽度越小，单色程度越高．实际得到的干涉条纹往往是不同波长的多套干涉条纹的叠加．每一光源发出的光都不可能是单一波长的谐波，而是有一定波长范围的准单色光[1]．通常的干涉条纹往往由这类准单色光获得．多长的谱线宽度的准单色光能够获得较为明显的干涉条纹，成为利用干涉原理进行工程测量的基本问题．杨氏双缝干涉是典型的分波面干涉装置[2]，我们利用其原理通过计算机仿真分析了谱线宽度与干涉条纹的可见度关系，得出有用的结果．对于研究非单色性光源在工程测量中的应用具有参考意义．

2 理想单色光源下的杨氏干涉条纹的可见度

设杨氏双缝干涉中，两缝出射的相干光在空间P点相遇，该点的总光强为[2]

(1)

式中I1和I2分别为两束相干光的光强，Δφ为二者间的相位差，因两相干光束为同一光源发出，则有

I0=I1=I2

式(1)可写为

(2)

从式(2)可看出

Imax=4I0

Imin=0

由干涉条纹可见度的定义

看出在理想单色光源下，杨氏干涉条纹的可见度

V=1，条纹的反差最大，清晰可见．

3 非单色光源对杨氏干涉条纹可见度的影响

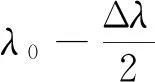
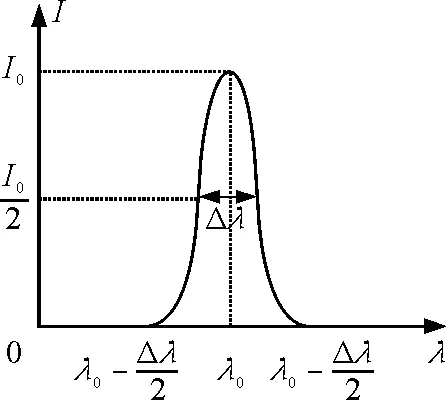
图1 非单色光源的谱线宽度

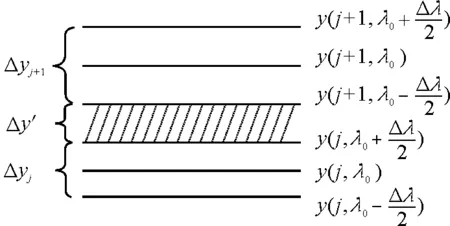
图2 第j级与第j+1级明条纹宽度及其间隔示意图

从图2可看出

(3)

从式(3)可看出Δy′与级数j跟谱线宽度Δλ有关，对于某一级数(即确定的观察点)的干涉条纹而言，Δλ越大，则Δy′越小，条纹可见度低，随着Δλ的不断增大，可见度逐渐变为零，此处条纹不可见．当Δλ继续增大，Δy′=0出现在小于j的级次处，则清晰可见的条纹数越少，直至观察不到干涉条纹．

4 Matlab仿真不同谱线宽度下的干涉条纹

根据杨氏双缝干涉理论，利用Matlab软件编程计算双缝干涉的光强分布并作图，同时模拟双缝干涉的条纹图样．在此基础上将不同谱线宽度光源的干涉光强分布进行叠加并得到叠加后的光强分布图及干涉图样[3]．

设双缝间距离d=0.12 mm，观察屏到缝的距离r0=1 000 mm，光源的中心波长λ0=500 nm，观察范围从中央亮纹位置(0 mm)到25 mm，干涉图样是在观察范围(25 mm)取100个采样点作灰度图，横坐标为采样点，纵坐标为观察屏上的横向范围．谱线宽度Δλ分别取10，30，50 nm，得到如图3，4，5所示的叠加前后的光强分布图及条纹图样．由图3，4，5中的光强分布图结合条纹可见度的定义式得到如图6所示的可见度大小分布曲线．

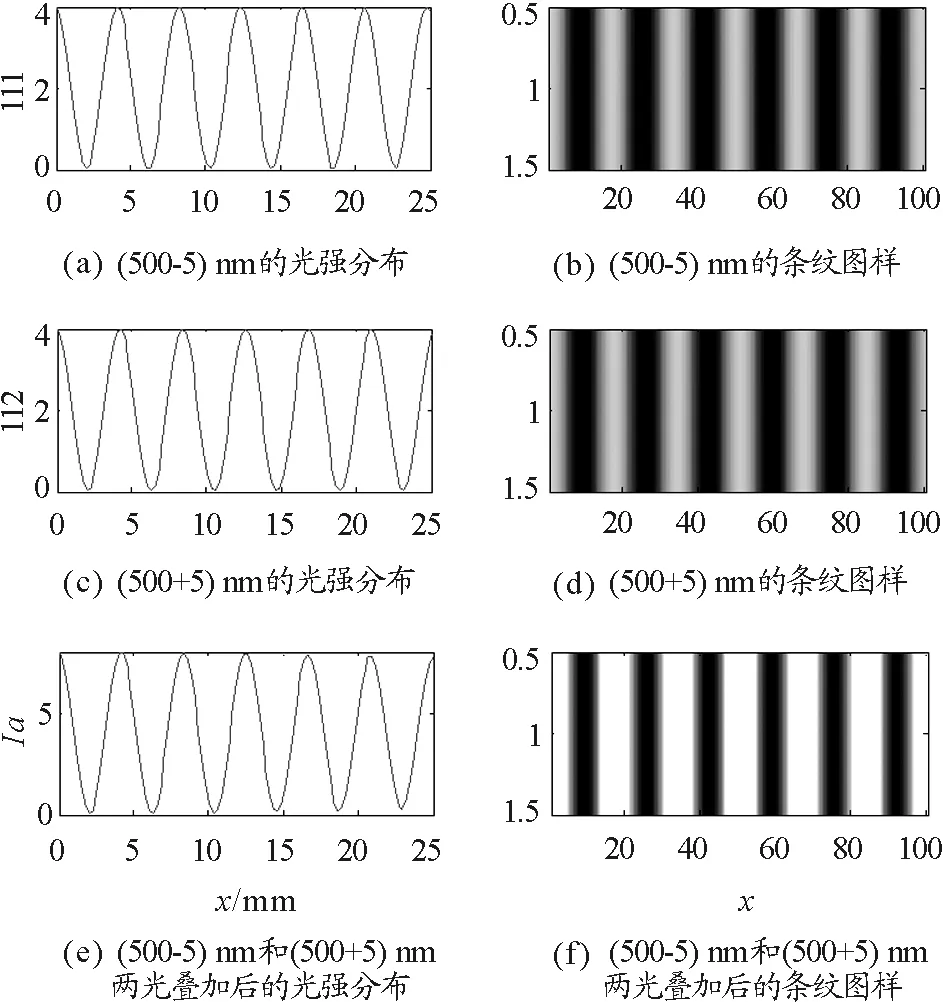
图3 Δλ=10 nm时的光强分布图及条纹图样

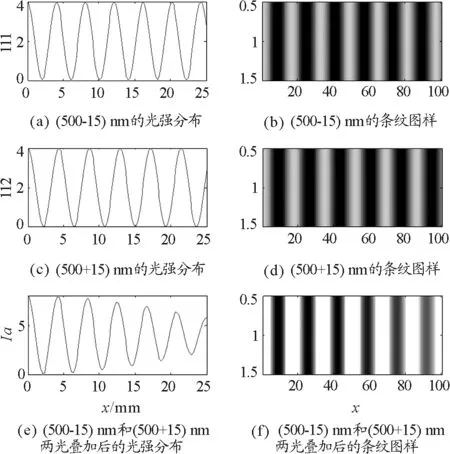
图4 Δλ=30 nm时的光强分布图及条纹图样

图5 Δλ=50 nm时的光强分布图及条纹图样

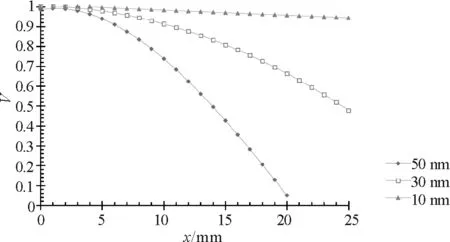
图6 条纹可见度分布曲线V-x

从图6可看出，观察范围内的条纹可见度随着观察位置的增大(即j越来越大)而减小，条纹逐渐变模糊．当Δλ=10 nm时，可见度值变化甚小，近似为1，条纹清晰可见，如图3(b)所示．Δλ逐渐增大，可见度随观察位置的增大减小得越快，出现模糊的条纹的位置越小，如图4(b)、5(b)所示，即观察范围内清晰可见的条纹数越少．对于某固定的观察点，此处的条纹可见度随着Δλ的增大而减小，与第3部分的理论分析结果一致．该结论与文献[4]中描述的实验结果相吻合，进一步说明了理论分析的合理性．

5 小结

本文通过一个简单的示意图对不同谱线宽度光源的干涉条纹进行理论分析，同时利用Matlab得到不同谱线宽度光源下的干涉条纹光强分布图、干涉条纹图样以及条纹可见度分布曲线，定性地分析了光源的非单色性，即谱线宽度，对干涉条纹可见度的影响：谱线宽度越小，光源的非单色性越好，条纹可见度变化越小，条纹清晰可见且能观察到的干涉条纹越多．与非单色光的实验结果相吻合，为利用非单色光源测量工程参量数提供了理论支撑．

1 廖延彪.现代光信息传感原理.北京：清华大学出版社，2009

2 姚启钧.光学教程(第5版). 北京：高等教育出版社,2004

3 王立明.计算机模拟光源的光谱强度分布对杨氏双缝干涉条纹的影响.高等函授学报(自然科学版),2007(05):45～49

4 石友彬,王文华,陈春雷，等.根据干涉条纹测量未知光源的波长.物理实验,2007(11):35～37，40

TheInfluenceofNonMonochromaticLightSourceontheYoungInterferenceFringeVisibility

ZhangYanZhaiYingHouYunlangZhuKun

(DepartmentofPhysicsandElectronicScience,Liupanshuinormaluniversity,Liupanshui,Guizhou553004)

The monochromatic light source affects its coherence.The visibility of interference fringe was directly affected by linewidth. what generally comprise wave trains shows light source quality. In this paper，Young's double-slit interference device produces interference fringes by Non-monochromatic light source is analysed and simulated,It’s show that the Relationship between Spectral Line Width and Visibility of Interference,from which we obtain the following conclusions.It’s a result for the light interfering method has the realistic meaning.

interference fringes;visibility;non-monochromatic light source

*贵州省教育厅本科教学质量工程教学内容与课程体系改革课堂基金，编号：GZSJG10977201403；六盘水师范学院2015年度大学生科研项目，编号：LPSSYDXS1511

张燕(1993- )，女，2013级应用物理学本科生.

祝昆(1976- )，男，副教授，主要从事光学教学研究.

2016-12-29)