一个新耦合ZK系统的对称, 精确解和守恒律①

李会会 李 玉 刘希强

(聊城大学数学科学学院,山东聊城252059)

一个新耦合ZK系统的对称, 精确解和守恒律①

李会会 李 玉 刘希强

(聊城大学数学科学学院,山东聊城252059)

利用修正的CK直接约化方法, 对一个新的耦合ZK系统的对称理论进行研究, 从而得到了耦合ZK系统的新旧解之间的关系,并进一步利用已知解求出了该系统新的精确解. 基于所求出的对称形式及耦合ZK系统共轭方程组的解, 得到了耦合ZK系统无穷多的守恒律.

耦合ZK系统, 精确解, 守恒律, 修正的CK直接约化方法

0 引言

近几十年来, 在科学技术的研究中演化出大量的非线性发展方程, 用以描述物理、生物等领域中的复杂现象. Zakharov-Kuznetsov(ZK)方程

ut+auux+b(uxx+uyy)x=0

是数学物理中一类重要的高维非线性演化方程. 1974 年,从含有冷离子和热等温电子的磁化等离子演化过程中Zakharov和Kuznetsov最先推导出该方程. 经研究发现,ZK方程也可以用来描述耦合非线性传输线中的非线性波与水波在(2+1)维空间中的运动规律. 因此, 对于求解该方程的研究具有重要的实际意义.

最近, 文献[1]从原有的ZK方程出发, 对此进行推广, 得到一个如下形式的新耦合ZK系统

(1)

其中α,β,γ,λ是任意常数. 文献[1]利用推广的Tanh-coth方法和双曲函数展开法, 得到了耦合ZK系统的孤立波解和周期波解. 可以发现, 当取u=ρ=w时, 方程组(1)可以简化为通常的ZK方程. 由此可见, 方程组(1)是单个ZK方程的推广.

由于, 非线性发展方程的精确解在解释物理、动力学等科学领域中的一些复杂现象有着非常重要的作用, 因此数学家和物理学家对非线性发展方程的求解问题作了大量研究. 迄今为止, 已经提出一些直接有效的求解方法, 如齐次平衡法, 双曲函数法,Tanh-coth方法,Jacobi椭圆函数展开法等. 利用这些方法能够求得非线性方程的一些冲击波解、孤立波解以及广义上的周期解. 尤其是楼森岳教授和马红彩教授在李群理论的基础上对CK直接约化方法进行推广, 提出了修正的CK直接约化方法[2],以便对方程的群变换解及守恒律进行系统的研究. 在文献[3]中, 利用李群方法得到了GZK方程的多项式解和三角函数解, 在文献[4]中, 借助李群理论得到了(2+1)维扩展ZK方程的对称、约化方程和精确解, 在文献[5]中, 利用直接约化方法得到了广义KdV-Zakharov-Kuznetsev方程的对称约化、精确解和守恒律.

1 耦合ZK系统新的精确解

假设方程组(1)有满足如下形式的变换

(2)

这里的ξ=ξ(x,y,t),η=η(x,y,t)和τ=τ(x,y,t)都是待定函数, 并且在变换

{u,ρ,w,x,y,t}→{U,V,W,ξ,η,τ}，

下要求U(ξ,η,τ),V(ξ,η,τ)和W(ξ,η,τ)也满足方程组(1), 即

(3)

令a1(x,y,t)=0,a2(x,y,t)=0,a3(x,y,t)=0, 把方程(2)代入方程组(1), 并利用方程组(3), 借助Maple软件得到下述决定方程组

(4)

解上述超定方程组得到

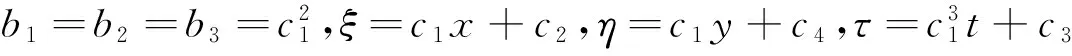
(5)

其中ci=0(i=1…4)是任意的常数.

根据上述过程, 我们有下面的对称群定理:

定理1 若U(ξ,η,τ),V(ξ,η,τ)和W(ξ,η,τ)是耦合ZK系统的解, 那么

(6)

也是耦合ZK系统的解, 其中ξ,η和τ由(5)式决定.

由定理1可以看出耦合ZK系统的新旧解之间的关系. 利用定理1, 可以由它的已知解得到许多新解. 例如选取文献[1]中的解(3.6)和(4.2), 可以得到耦合ZK系统的新解

其中c,c1是任意常数,ξ=c1x+c2,η=c1y+c4,τ=c1t+c3.并且得出的新解的约束条件和文献[1]中解的约束条件相同. 类似地,可以根据方程组(1)的不同种子解重复利用定理1 , 就可以得到不同种类的精确解.

2 对称群的李代数

为了可以更好的分析(5)式所对应方程组的李代数, 取

c1=1+εc1,c2=εc2,c3=εc3,c4=εc4,

其中ε是无穷小参数, 且ci=0(i=1…4)是任意的常数, 那么方程(6)可记作

u=U+εσ(U),ρ=V+εσ(V),w=W+εσ(W) ，

(7)

(8)

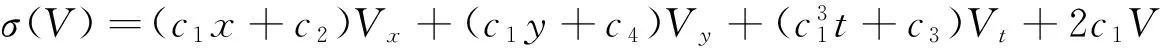
(9)

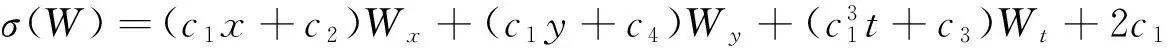
(10)

与上述对称等价的向量场可以表示成

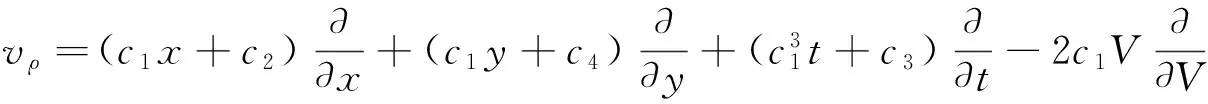
同时向量场vu,vρ和vw也可由李点变换群方法计算得到. 这里由(8), (9), (10)式表达的是耦合ZK系统的对称. 对称群的等价算子表达式为

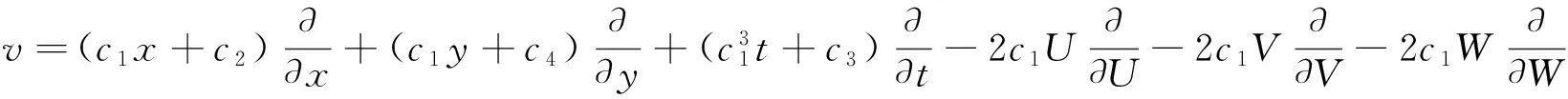
(11)

由(11)式可以得到

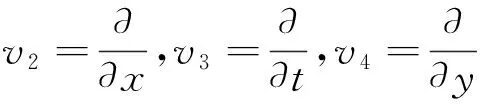
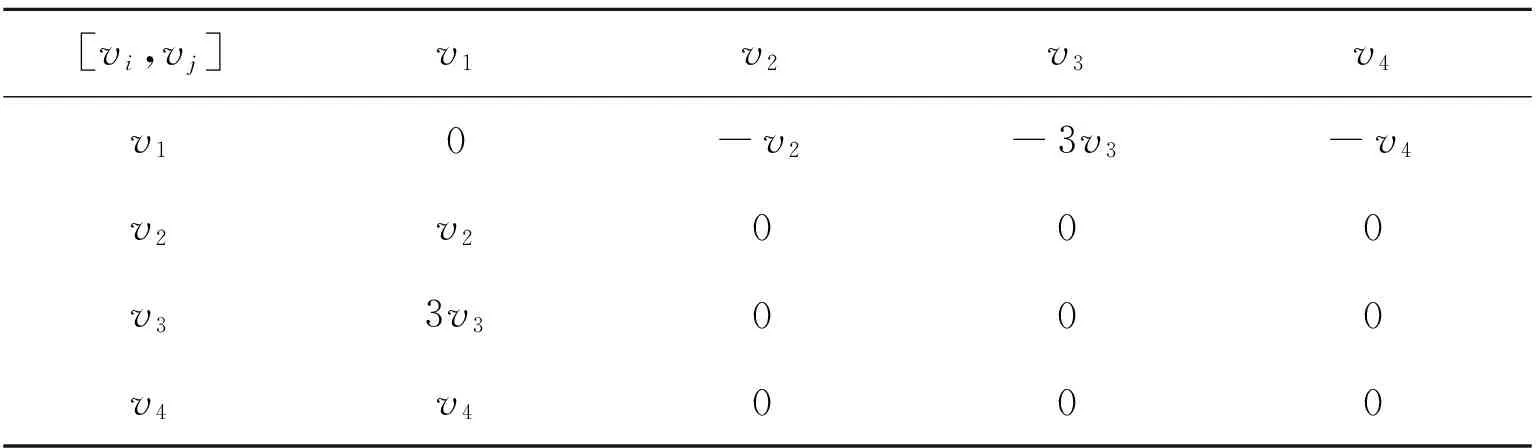
易验证上述对称之间的算子关系为

[vi,vj]v1v2v3v4v10-v2-3v3-v4v2v2000v33v3000v4v4000

由上述算子关系可以看出,方程组(1)满足四维的李代数.

3 耦合ZK系统的守恒律

我们将通过耦合ZK系统的共轭方程组和已求得的对称来研究它的守恒律. 耦合ZK系统的共轭方程组为

(12)

三阶拉氏函数为

L=v1(ut-α(uρ)x-γ(ρw)x-β(uxx+uyy)x)

+v2(ρt-λ(uw)x-β(ρxx+ρyy)x)+v3(wt-λ(uρ)x-β(wxx+wyy)x).

(13)

二阶拉氏函数为

L=v1(ut-α(uρ)x-γ(ρw)x)+βv1x(uxx+uyy)+v2(ρt-λ(uw)x)

+βv2x(ρxx+ρyy)+v3(wt-λ(uρ)x)+βv3x(wxx+wyy).

(14)

定理2[6]每个李点对称、李贝克隆变换和方程组(1)的对称都给出了耦合的ZK系统及其共轭方程组的一个守恒律, 且守恒向量由下式给出

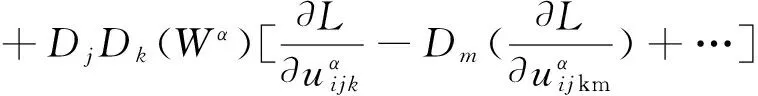
(15)

在此, 我们考虑耦合ZK系统的二阶拉氏量, 利用定理1和公式(15)计算耦合ZK系统的守恒律. 规定, 我们有

ξ1=3c1t+c3,ξ2=c1x+c2,ξ3=c1y+c4,

η1=-2c1u,η2=-2c1ρ,η3=-2c1w,

w1=-2c1u-(3c1t+c3)ut-(c1x+c2)ux-(c1y+c4)uy,

w2=-2c1ρ-(3c1t+c3)ρt-(c1x+c2)ρx-(c1y+c4)ρy,

w3=-2c1w-(3c1t+c3)wt-(c1x+c2)wx-(c1y+c4)wy.

在上述条件下,(15)式满足守恒方程Dt(C1)+Dx(C2)+Dy(C3)=0, 且向量的元素为

由对称(8)、(9)和(10), 取c1=1,c2=c3=c4=0, 可得

C1=-x(uxv1+ρxv2+wxv3)-y(uyv1+ρyv2+wyv3)-

t(utv1+ρtv2+wtv3)-2(u+ρ+w),

C2=x(uxA+ρxB+wxD-β(uxxv1x+ρxxv2x+wxxv3x)+

y(uyA+ρyB+wyD-β(uxyv1x+ρxyv2x+wxyv3x)),

C3=βx(uxv1xy+uxyv1x+ρxyv2x+ρxv2xy+wxv3xy+wytv3x)+

βy(uyv1xy+uyyv1x+ρyv2xy+ρyyv2x+wyv3xy+wyyv3x)+

3βt(utv1xy+ρv2xy+wtv3xy+uytv1x+ρytv2x+wytv3x)+

2β(uv1xy+ρv2xy+wvv3xy)-3β(uyv1x+ρyv2x+wyv3x),

其中A=v1αρ+v2λw+v3λρ+βv1xx;B=v1αu+v1γw+v3λu+βv2xx;D=v1γρ+v2λu+βv3xx.

借助于Maple软件, 我们可以验证上述求得的向量是方程组(1)的守恒向量,这个守恒向量也包含了共轭方程组(12)的任意解, 因此上式给出了耦合ZK系统的无穷多个守恒律.

考虑方程组(12)的特解v1=v2=v3=1, 那么我们得到方程组(1)的一组守恒向量

C1=-x(ux+ρx+wx)-y(uy+ρy+wy)-t(ut+ρt+wt)-2(u+ρ+w),

C2=x(ux(αρ+λw+λρ)+ρx(αu+γw+λu)+wx(γρ+λu))+y(uy(αρ+λw+λρ)+ρy(αu+γw+λu)+wy(γρ+λu))+3t(ut(αρ+λw+λρ)+ρt(αu+γw+λu)+wt(γρ+λu))+2(u(αρ+λw+λρ)+ρ(αu+γw+λu)+w(γρ+λu)),

C3=0.

4 结论

对一个新的耦合ZK系统利用修正的CK直接约化方法, 求得了该系统的对称, 继而得到了其新旧解之间的关系, 利用文献[1]中耦合ZK系统的已知解,得到了新的精确解. 最后利用已求得的对称及其共轭方程组,得到了耦合ZK系统的无穷多守恒律. 由此可见，本文中用到的方法对于求解非线性演化方程(组)具有非常重要的作用.

[1]WeiMin-zhi,TangSheng-qiang.ExactexplicittravellingwavesolutionsforanewcoupledZKsystem[J].JournalofAppliedAnalysisandComputation, 2011, 21(7): 267-277.

[2]LouSen-yue,MaHong-cai.Non-liesymmetrygroupsof(2+1)-dimensionalnonlinearsystemsobtainedfromasimpledirectmethod[J].JournalofPhysicsAGeneralPhysics, 2005, 38(7): 129-137.

[3]YanZhi-lian,LiuXi-qiang.SymmetryReductionsandExplicitSolutionsforaGeneralizedZakharov-KuznetsovEquation[J].CommunicationsinTheoreticalPhysics, 2008, 45(1): 29-32.

[4] 李康，刘希强. (2+1)维扩展Zakharov-Kuznetsov方程的对称、精确解和守恒律[J].井冈山大学学报，2015，36(3):29-33.

[5] 于兴江.广义KdV-Zakharov-Kuznetsev方程的对称约化、精确解和守恒律[J].量子电子学报, 2014, 31(6): 670-677.

[6]NailHIbragimov.Anewconservationtheorem[J].JournalofMathematicalAnalysis&Applications, 2007, 333(1): 311-328.

[7] 刘勇，刘希强.Caudrey-Dodd-Gibbon方程相似、约化、精确解及守恒律[J].聊城大学学报:自然科学版, 2014, 27(1): 9-24.

[8]XieYong-an,TangSheng-qiang.Sine-CosinemethodfornewcoupledZKsystem[J].AppliedMathematicalSciences, 2011(21-24): 1 065-1 072.

[9]Abdul-MajidWazwaz.TheextendedtanhmethodfortheZakharov-Kuznetsov(ZK)equation,themodifiedZKequationanditsgeneralizedforms[J].CommunicationsinNonlinearScience&NumericalSimulation, 2008, 13(6): 1 039-1 047.

[10] 陈美,刘希强,王猛.对称正则长波方程组的对称,精确解和守恒律[J].量子电子学报,2011, 29(1): 21-26.

[11]DongZhong-zhou.ExacttravellingwavesolutionsofnonlinearcoupleKDVequations[J].ChineseJournalofQuantumElectronics,2006, 23: 379-382.

[12]WazwazAM.TheextendedtanhmethodfornewcompactandnoncompactsolutionsfortheKP-BBMandtheZK-BBMequations[J].ChaosSolitons&Fractals, 2008, 38(5): 1 505-1 516.

[13]XinXiang-peng,LiuXi-qiang,ZhangLin-lin.SymmetryReductionsandExplicitSolutionsof(2+1)-dimensionalnonlinearevolutionequation[J].JournalofJinggangshanUniversity, 2012, 45(8): 71-75.

[14] 李康,刘洪吉．广义MKP方程的对称约化和精确解 [J].聊城大学学报:自然科学版, 2015, 28(1): 19-23．

[15]LiuNa,LiuXi-qiang,LuHai-ling.Newexactsolutionsandconservationlawofthe(2+1)-dimensionaldispersivelongwaveequations[J].PhysicsLettersA, 2009, 373(2): 214-220.

Symmetry Reductions, Exact Solutions and Conservation Law of a New Coupled ZK System

LI Hui-hui LI Yu LIU Xi-qiang

(School of Mathematical Sciences, Liaocheng University, Liaocheng 252059, China )

By using the modified direct reduction method presented by Clarkson and Kruskal, the symmetry group theorem of a new coupled ZK system are derived. Some new exact solutions of a new coupled ZK system are obtained by applying the theorem and given solution. Conservation laws of the equations are obtained with the corresponding Lie symmetry.

a new coupled ZK system，exact solutions，conservation laws，modified CK’s direct reduction method

2016-11-26

国家自然科学基金与中国工程物理研究院基金项目(11076015)资助

刘希强，E-mail:liuxiq@sina.com.

O175.2

A

1672-6634(2017)01-0005-05