双优无标度网络模型*
马飞,姚兵
(西北师范大学数学与统计学院, 甘肃 兰州 730070)
双优无标度网络模型*
马飞,姚兵
(西北师范大学数学与统计学院, 甘肃 兰州 730070)
基于标准的无标度网络模型,首先扩展了网络增长的“优先连接机制”原则,从更一般的情形出发,设立不同约束条件下的点优先连接概率,既而建立了更一般的网络动力系统所符合的偏微分方程,给出无标度网络的一个拓扑性质。然后,给出了一种更加符合现实的择优概率,接着,建立了一类更一般的网络演化模型,并讨论了它的无标度特性,得到它的幂率指数γ在1~4之间。
无标度网络模型;动态演化;偏微分方程;六度分离
我们生活的世界中充满了无数的网络,如细胞中的新陈代谢网、大脑中的神经网、生态系统中的食物链网、社会关系网络、科研合作网络、经贸互惠网络、互联网、万维网以及电力网和交通运输网等等。这些网络都能被抽象成网络模型——图,起初研究者们运用图论的方法做研究,但是图论中研究的图形大多都是规则的、单一的,但真实网络的结构不仅很复杂的,而且构成网络的节点数目也是很庞大的,这样一来,网络研究对传统经典图论的发展提出了新的要求。上世纪50年代,Erdös等基于经典图论的研究,提出了随机网络模型(ER模型)该模型能很好的体现网络的随机性,但是节点的度(与节点相连接的边的数目)之间相差不大,几乎相等,度分布服从Poisson分布,其图像是一条钟型曲线。显然,真实网络中节点的度并不是相等的。为了解释蕴含在网络中的规律,Watts等[1-2]提出了小世界网络模型,该模型在继承了随机网络模型的随机性后,出现了新的网络拓扑性质:属于该网络模型中初始节点的度相对要大一些,它的度分布呈现出指数衰减。1999年,基于万维网拓扑结构的研究,Barabási等[3]发现钟型曲线消失了,出现了一条递减的曲线,为了刻画这一结果,他们首次提出了无标度网络模型(BA-模型),该模型满足幂率分布式
P(k)≈k-γ
(1)
其中γ叫做无标度指数,它的取值范围是2<γ<3。在他们首创性的研究工作之后,复杂网络的研究得到了众多科研人员的重视,经过大量研究后发现:生活中大量的网络都具有无标度特性(scale-freeproperty),即服从幂率分布(1),但部分真实网络的幂律指数γ的取值范围却超出了2~3,落在1~4之间[4]。通过计算机仿真模拟后,确实证明了这一点[5-7]。
近年来,国内外的研究人员对BA-模型进行了不同层次的推广和拓展,得到的成果颇多。但在这些研究中,人们认同网络中存在“先到先得,富者越富,适者更富”现象。针对这种现象,总结得出具有无标度特性的网络演化(增长)必须满足2条性质:均匀增长和择优连接。特别是择优连接方式对一个演化的网络是否具有无标度特性起到决定性的作用,已证实运用线性择优连接方式将会得到无标度网络,非线性的择优连接方式将会影响到网络的度分布,使其不再服从幂率分布[8]。
1 一般形式的动态微分方程
在Barabási等[3]提出无标度网络模型(BA-模型)之后,研究人员不论是采取理论研究手段,还是采用计算机仿真模拟,他们对网络动态演化的描述与刻画都存在着相似之处[4],都是讨论随着时间的延续,网络中不断地会有外界新的节点进入,同时,网络自身内部也发生着变化(如:网络中未连边的节点之间由于某种联系而产生新的连边),随着这种演化方式的进行,网络的规模会变得越来越庞大,但是这种增长方式不可能无休止地进行下去,在历经一段时间的增长后,网络的规模就会趋于稳态或衰退,即网络中出现节点“湮灭”和旧边被“删除”。对一个最初具有m0个节点的网络N(0)而言,假设它的动态演化是连续的,t时刻后,对网络N(t)中一个度为ki(t)的节点,依据事件的独立性给出一个动态方程[9]:
h*(t)+z*(t)+φ(t)
(2)
方程(2)右端有5个功能函数:加点函数(优先连接函数)f*(t)=f(ap1(t)m,t,ki(t),∏1(ki))的含义是:t时刻有a个“新”节点进入到网络N(t-1)中,每个“新”节点与网络N(t-1)中已存在的节点间连接产生p1(tm条新边(0 设方程(2)的解为ki(t)=θ(t,ti,α1,α2,…,αr),其中参数αi(i=1,2,…,r)与时间变量t和ti无关。进一步,得 P(ki(t) (t,ti,β1,β2, …,βr)) (3) 方程(3)中的参数βi(i=1,2,…,r)与时间变量t和ti均无关,上述方程(3)中的记号θ-1(t,ti,β1,β2,…,βr)表示函数ki(t)的反函数。解得网络N(t)中顶点度数为k的概率 (4) 本文以文献[6,10-12]中的结论来解释由方程(2)所建立的模型,尝试对复杂网络进行综合性的研究。包括演化网络所符合的动态微分方程、择优连接方式、如何进行网络之间比较、如何优化网络等方面,并建立一种幂律指数γ的取值范围在1到4之间的无标度网络模型(双优无标度网络模型)。 通过对大量现实网络的研究,人们认识到几乎所有的网络都表现出无标度特性,为了更好地模拟无标度网络,从理论上出发,研究者们建立研究方法,并通过计算机进行仿真模拟。然而经验告诉我们:网络的动态演化中包含增长与衰退,许多研究学者都认为网络以“择优”方式进行增长,以“反择优”方式进行衰退。在Barabási等[3]首次提出线性择优增长模型之后,研究者们依此为基础,对“择优”方式进行了不断地改进、完善,相应地建立了不同的网络模型,从不同的侧重点进行刻画、模拟现实生活中已存在的网络,并对网络的动态演化特征做出一些相关的预测,同时也为建立新的更加健全的网络模型提供理论支持。 在本文中,t时刻的网络模型记为N(t),它的节点集合和边集合分别是V(t)和E(t),网络模型N(t)的节点个数是nv(t)=|V(t)|,它的边数目是ne(t)=|E(t)|,ni(t)表示N(t)中节点度数为ki的节点数目。 3.1 陈庆华等模型 陈庆华等模型的演化算法[13]:步骤1、在已存在的节点中添加l条新边:随机选择一个节点作为与新边连接的起始点,点i被选择作为新边另一节点的概率满足 (5) (6) (7) 由(7)式可得 (8) 3.2 梁洪振等模型 (9) (10) 由(10)式可得 m+2n-2c (11) 和式(11)的结果是一个常数。 3.3 贾秀丽等模型 以及φ(t)=0,易得网络动态演化满足下面的方程 (12) (解释上式每一项的含义,第1项新节点加入到网络中引起ki的变化,第2项是随机删除节点引起ki的变化,第3项是网络择优加边引起ki的变化(第一部分:节点i依择优概率∏(ki)被选作所加边的起始节点时引起度发生变化;第二部分:节点i依择优概率∏(ki)被选作所加边的另一节点时引起度发生变化),第4项是网络反择优删除边引起ki的变化(第一部分:节点i依反择优概率p-1(ki)被选作所删边的起始节点时引起度发生变化;第二部分:节点i依反择优概率p-1(ki)被选作所删边的另一节点时引起度发生变化))。在t时刻节点的平均度为 将nv(t)、ne(t)代入方程(12),得到一阶近似微分方程 (13) 因此 (14) 所以节点的度分布: 其中幂率指数 对(12)式求和,得到 (15) 当t→∞时, m+2r-2n 我们得到一个结论:在网络动态演化的过程中,对相应的动态方程(2)求和后将等于一个常值M,并且M就等于每一时刻网络的动态变化值。 针对现实生活中确实存在幂律指数γ>3的无标度网络(例如:SexualContacts网络的幂律指数γ=3.4[16],本文建立一类网络模型,它不仅能很好的说明该类无标度网络的存在性,而且还可以包含经典的BA模型。基于构造BA模型的均匀增长、优先连接算法,几乎当前所有的网络模型都认为新节点的加入、新边的产生都完全地遵循优先连接,旧节点的删除、旧边的删除都绝对地遵循反择优删除。但是绝对的事实并非都完全成立,例如:在科学家合作网络中,刚出道的年轻研究者往往渴望与著名专家合作,进行科研(只要有机会),但在随机的情况下有时会与一位同样年轻的研究者进行合作。这种现象在网络演化模型中可以解释为:刚进入网络的新节点,在采用优先连接概率与已存在于网络中的旧节点连边时,会随机的与节点度数不大(甚至很小)的节点进行连边运算,但是连边的过程中优先连接概率起主要的支配作用。同样的道理,在删除旧边的过程中,并不是所有被删除的边都采用反择优概率,偶尔也会出现随机删边的现象,但反择优概率在删边运算中起决定作用[17-20]。 鉴于此种现象的确存在,本文提出了优选优先连接概率与优选反择优删除概率。如下: ①优选优先连接概率 ∏1=α∏11+(1-α)∏12 其中∏11表示优先连接概率,∏12表示随机连接概率,参数α(1/2≤α≤1)意指“优选”,即在概率∏1中,∏11起支配作用。 ②优选反择优删除概率 ∏2=(1-β)∏21+β∏22 其中∏21表示反择优概率,∏22表示随机删除概率,参数β(0≤β≤1/2)意指“优选”,即在概率∏2中,∏21起支配作用。 按照上面的优选优先连接概率与优选反择优删除概率,本文构造了如下的双优无标度网络模型N(t):初始网络N(0)是具有m0个节点、n0条边的简单连通图。从t>1时刻起,网络模型将执行以下两个操作进行演化。 1) 优选优先连接(1/2≤α≤1):t时刻有a个节点加入网络N(t-1)中,每个新节点分别采用优选优先连接概率∏1与已存在于网络模型中的m个不同节点连边。度数为ki的旧节点获得与新节点连边的概率满足如下关系: ∏1=α∏11+(1-α)∏12= 2)优选反择优删除(0≤β≤1/2):t时刻有b条边从网络N(t-1)中分别采用优选反择优概率∏2被删除。每条被删除边的一个节点随机选取,选择另一个节点时按优选反择优概率 ∏2=(1-β)∏21+β∏22= 经历这样的t次演化后,网络模型N(t)具有m0+at个节点和n0+(am-b)t条边。显然当参数a=1,b=0,α=1,β=0时,该网络模型就退化成BA-模型。 假设ki是连续实变量,根据模型的演化机理,在方程(2)中,取加点函数 删边函数 删边函数z*(t)中的第1项b/{n0+amt-bt}表示节点i被随机选中作为起始节点时引起度的变化,第2项b∏2表示节点i被采用优选反择优删除概率选中作为另一节点时引起度的变化,g*(t)=h*(t)=φ(t)=0。则有如下动态方程: (16) 进一步可得: M(t)ki+R(t) 在初始条件ki(ti)=m下,上述一阶微分方程的通解为: (17) 其中h=amα-bβ,l=2(am-b)。网络中任选一个节点度数为ki(t)且不超过k的概率可以被写成如下: (18) 假设插入“新”节点到网络中的时间t服从均匀分布,即P(ti)=1/(m0+t),便可得到节点的度分布函数 (19) 当t充分大时, 网络度分布服从幂率分布,且幂率指数 现对该双优无标度网络模型的幂律指数γ=l/h+1进行分析。当α=1/2,β=1/2时,γ=l/h+1=4;当α=1,β=0时,γ=l/h+1<3;当α=2/3,β=1/3时,γ=l/h+1=3。所以幂律指数γ的范围为 对(16)式进行求和计算得 (20) 当t充分大时,(20)式的左端趋近于常数 本文提出了一种新的择优连接规则,开始尝试用纯数学方法(动力系统+偏微分方程)来解释网络演化的动态特征,通过对几类特殊动态网络演化模型的理论分析,进一步的说明用偏微分方程去刻画这一动力系统的必要性和重要性。然后依据本文中的分析建立了一类新的网络模型,不仅讨论了它的无标度特性,同时也验证了新发现——对动态方程(2)求和后值将是一个常数。作为今后的研究,提出下面的问题: 问题1 如何优化网络?前期对择优率(增长)的大量研究都局限于线性结构,是否生活中的网络都是线性择优增长的?为此,本文分析了一类简单的非线性择优增长率 (21) 问题 2 从不同的考察角度和侧重点,研究者们建立的各种模型都是基于方程(2)中概率参数pi(t)=1(i=1,2,3,4),在这种极为特殊的情形下,问题的讨论将变得具体、可操作,但现实生活中网络的演化是相当复杂的,每一时刻进入网络的节点数目、从网络中“湮没”的节点数目、网络中删除“旧”边的数目、网络中重新连接边的数目等都是变化的,所以有必要研究方程(2)中诸概率参数pi(t)=1(i=1,2,3,4)不是定值的网络演化情形。 注意根据六度分离定理,忽略与节点i距离超过6的节点的影响系数,那么就可以定义关于节点i的择优概率为 (22) 选取,式中ϑi表示与节点i之间距离为1的节点构成的集合(也称节点i的1-邻居集)。如果网络中已存节点间要有新边产生时,新边的一个节点可以随机选择,完美的情形下另一个节点应该是r(1 [1]WATTSDJ,STROGATZSH.Collectivedynamicsofsmall-worldnetworks[J].Nature, 1998, 393:440-442. [2]WATTSDJ.Smallworlds:thedynamicsofnetworksbetweenorderandrandomness[M].Princeton:PrincetonUniversityPress, 1999. [3]BARABSIAL,ALBERTR,JEONGH.Mean-fieldtheoryforscale-freerandomnetworks[J].PhysicaAStatisticalMechanics&ItsApplications, 1999, 272(1/2): 173-187. [4] 刘浩广, 蔡绍洪, 张玉强. 无标度网络模型研究进展[J]. 大学物理, 2008, 27(4): 43-47.LIUHG,CAISH,ZHANGYQ.Theresearchonthescale-freenetworksmodel[J].CollegePhysics, 27(4): 43-47. [5]YAOB,LIUX,ZHANGWJ,etal.ApplyingGraphtheorytotheInternetofThings[C]//IEEEInternationalConferenceonHighPerformanceComputingandCommunications, 2013: 2354-2361. [6]YAOB,YAOM,CHENXE,etal.Researchonedge-growingmodelsrelatedwithscale-freesmall-worldnetworks[J].AppliedMechanics&Materials, 2014, 513-517: 2444-2448. [7]YAOB,YANGC,YAOM,etal.Graphsasmodelsofscale-freenetworks[J].AppliedMechanics&Materials, 2012, 380-384: 2720-2723. [8]KRAPIVSKYPL,REDNERS,LEYVRAZF.Connectivityofgrowingrandomnetworks[J].Physics, 2000, 85(21): 4629-4632. [9]MAF,SUJ,YAOB,etal.Scale-freenetworkmodelswithparameters[C].JointInternationalInformationTechnology,MechanicalandElectronicEngineeringConference, 2016, 59: 155-162. [10]SONGC,KORENT,WANGP,etal.Modellingthescalingpropertiesofhumanmobility[J].NaturePhysics, 2010, 6(10): 818-823. [11]YANG,TSEKENISG,BARZELB,etal.Spectrumofcontrollingandobservingcomplexnetworks[J].NaturePhysics, 2015, 11(9): 779-786. [12]DELGENIOCI,GROSST,BASSLERKE.Allscale-freenetworksaresparse[J].PhysicalReviewLetters, 2011, 107(17): 178701-178701. [13]CHENQ,SHID.Themodelingofscale-freenetworks[J].PhysicaAStatisticalMechanics&ItsApplications, 2004, 335: 240-248. [14] 梁宏振, 姚洪兴, 张学兵. 一类无标度网络的特征分析[J]. 复杂系统与复杂性科学, 2005, 2(3): 67-71.LIANGHZ,YAOHX,ZHANGXB.Charactersanalysisforaclassofscale-freenetworks[J].ComplexSystems&ComplexityScience, 2005, 2(3): 67-71. [15] 贾秀丽, 蔡绍洪, 张芙蓉. 一种动态的无标度网络模型[J]. 四川师范大学学报(自然科学版), 2009, 32(6): 839-842.JIAXL,CAISH,ZHANGFR.Adynamicscale-freenetworkmodel[J].JournalofSichuanNormalUniversity(NaturalScience), 2009, 32(6): 839-842. [16] 王林, 戴冠中. 复杂网络的度分布研究[J]. 西北工业大学学报 (自然科学版), 2006, 24(4):405-409.WANGL,DAIGZ.Ondegreedistributionofcomplexnetwork[J].JournalofNorthwesternPolytechnicalUniversity, 2006, 24(4):405-409. [17]YAOB,MAF,SUJ,etal.Scale-freemultiple-partitemodelstowardsinformationnetworks[C]//Proceedingsof2016IEEEAdvancedInformationManagement,Communicates,ElectronicandAutomationControlConference(IMCEC2016), 2016: 549-554. [18]SUJ,MAF,YAOB,etal.AS-mixednetworkmodelscreatedbytriangle-expandingoperations[C]//JointInternationalInformationTechnology,MechanicalandElectronicEngineeringConference(JIMEC2016), 2016, 59: 260-265. [19] 王晓敏, 赵喜杨, 姚兵. 全边增长网络模型的生成树[J]. 中山大学学报 (自然科学版), 2016,55(1): 48-53.WANGXM,ZHAOXY,YAOB.Spanningtreesoftotallyedge-growingnetworkmodels[J].ActaScientiarumNaturaliumUniversitatisSunyatseni, 2016,55(1): 48-53. [20] 杨俊仙, 闫萍.一类具饱和发生率的时滞SEIR传染病模型的分析[J]. 中山大学学报 (自然科学版), 2015, 54(3): 51-55.YANGJX,YANP.AnalysisofadelayedSEIRepidemicmodelwithsaturationincidence[J].ActaScientiarumNaturaliumUniversitatisSunyatseni, 2015, 54(3): 51-55. Double preferential scale-free network models MAFei,YAOBing (College of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,China) Based on the “classic” scale-free network model, the network growth principle(preferential attachment mechanism) is extended. Starting from a more general situation, some vertex-preferential attachment probability in different constraint conditions are established, and then the partial differential equation satisfied a more general network dynamic system is set up, and also another important topological property of scale-free network is found. Then a much realistic preferential attachment probability is presented. Finally, a more general network model is generated. By discussing its scale-free property, that scale-free parameterγrangesfrom1to4iscaptured. scale-free network model; dynamic evolution; partial differential equation; the six degrees of separation 2016-05-18 基金项目:国家自然科学基金 (61662066,61163054,61363060) 马飞(1992年生), 男;研究方向:动态图论与复杂网络;E-mail: mafei123987@163.com 姚兵(1956年生);男;研究方向:动态图论与复杂网络; E-mail: yybb918@163. com 10.13471/j.cnki.acta.snus.2017.01.014 O A 0529-6579(2017)01-0085-082 设立反择优连接的标准





3 满足方程(2)的网络模型

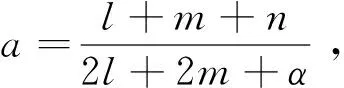
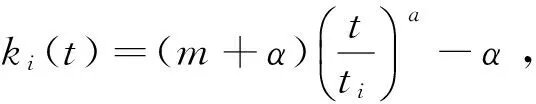


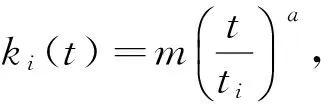



4 双优无标度网络模型
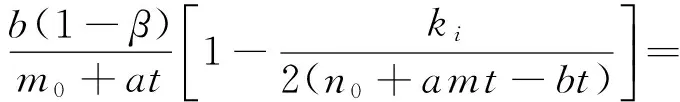
5 总结及问题