采用神经网络算法的多指机械手织物抓取规划

张 蕾， 韦攀东， 李鹏飞， 王晓华， 刘秀平

(西安工程大学 电子信息学院， 陕西 西安 710048)

采用神经网络算法的多指机械手织物抓取规划

张 蕾， 韦攀东， 李鹏飞， 王晓华， 刘秀平

(西安工程大学 电子信息学院， 陕西 西安 710048)

针对纺织服装行业织物自主抓取环节依靠人工操作而导致的生产效率低的问题，利用机械手进行织物抓取。设计了多指机械手，通过描述手指各连杆之间的变换关系对其进行运动学分析；采用RBF(径向基函数)神经网络方法对其抓取模式进行规划，通过识别织物的几何特征并根据抓取的任务要求进行自主抓取；在抓取运动过程中，采用关节空间轨迹规划和笛卡尔空间轨迹规划相结合的方式，保证机械手各手指能够稳定和准确地到达抓取点；最后利用MatLab/Robotics Toolbox对多指机械手和抓取规划进行建模仿真。结果表明，所设计的机械手各个关节参数设置合理，机械手织物抓取规划满足要求。

多指机械手； 抓取模式规划； RBF神经网络； 轨迹规划； 织物抓取

随着“工业4.0”的到来以及机器人技术的逐渐成熟，“机器人换人”以减少用工，提高生产效率，将最终成为纺织服装企业的现实选择。机械手是安装在机器人末端的执行机构，它有效地弥补了传统工业机器人抓取方式单一的不足[1-2]。机械手具有拟人手的特性，它高度的灵活性使得通过对其进行合理的抓取规划能够实现对任意形状物体的抓取操作[3]。在纺织服装行业中，有很多生产工艺流程的连接是依靠人工完成的，例如自动裁剪、自动配片、自动抓取、服装吊挂系统等，尤其对于自动抓取环节国内外研究甚少，导致了服装智能制造链的不完整。本文提出采用机械手解决柔软织物抓取的问题，对目前纺织服装行业的自动化进程具有重要的实际意义。

人们在进行物体抓取时，抓取对象的形状、大小以及位姿参数构成了抓取模式分类的重要依据[4-6]。目前，多指机械手抓取模式规划大都采用基于知识的方法，通过学习或其他方式不断扩充来对知识库进行更新，具有计算量小，易实现的优点。但知识库的建立是一个漫长的过程，而且之前建立的规则难免会与新的规则发生冲突，不能保证系统的完整性。RBF神经网络能够从环境中快速地学习并在学习中提高自身性能，具有最佳局部逼近能力[7-8]，采用它进行抓取模式规划是十分可行的。

本文结合柔软织物特性，设计多指机械手的结构并进行运动学分析；提出基于RBF神经网络的织物抓取模式规划，通过提取织物的几何特征并根据抓取的任务要求，建立抓取模式模型，实现自主抓取；对抓取运动过程进行轨迹规划，采用关节空间和笛卡尔空间混合的轨迹规划方式，保证整个抓取操作过程顺利完成；并利用MatLab/Robotics Toolbox对机械手和抓取运动过程进行建模仿真，仿真结果表明，机械手抓取运动轨迹规划合理，织物自主抓取操作规划过程是可行的。

1 机械手结构设计与运动学分析

1.1 机械结构设计

由于织物的堆放形状是不确定的[9-10]，因而对机械手的结构有很高的要求。2个手指能够实现对简单物体的抓取，但在手指接触点连线的旋转方向缺少1个约束条件，导致抓取不稳定。多于3个手指的机械手具有更高的灵活性，但存在冗余手指，随着冗余自由度的增多，控制更加复杂，这在实际的设计中是不可取的；因此，本文结合柔软织物的特性和机械手自身的性质，设计了机械手，结构如图1所示。机械手具有3个手指，各手指的结构和性质相似，每个手指有4个自由度，关节类型都为转动关节，且各手指关节轴1垂直于其余3个关节轴，保证机械手在操作空间中能够对织物进行任意抓取操作。

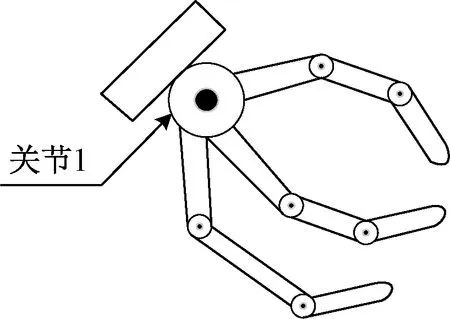
图1 三指机械手结构Fig.1 Structure of three-fingered dexterous hand

1.2 运动学分析

机械手运动学分析，即通过建立手指连杆之间的齐次坐标变换关系，从而求得手指指尖的位姿矩阵，获取指尖在操作空间中的位置和姿态。这里以1个手指作为研究对象，其余2个手指与此类似。采用D-H参数法进行运动学方程的建立，由所设计的机械手的结构可得到手指各关节量和连杆参数，如表1所示。

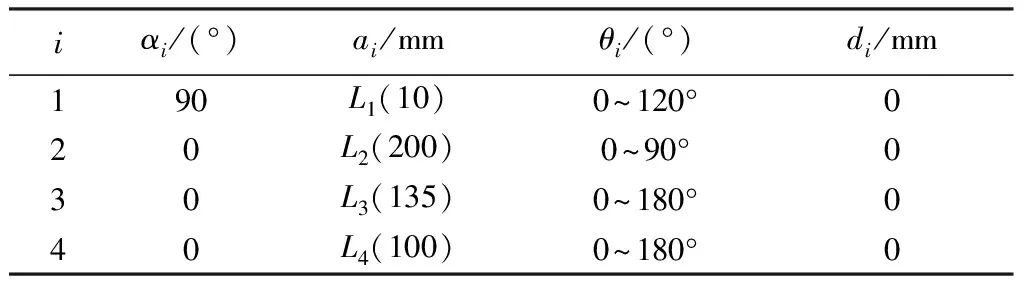
表1 手指连杆D-H参数表Tab.1 D-H parameters of fingers′ connecting rod

表中：αi代表连杆扭转角，表示相邻关节轴线之间的夹角；ai代表连杆长度，表示相邻关节轴线公垂线长度；θi代表关节角度，表示相邻公垂线之间的夹角；di代表偏置，表示相邻公垂线之间的距离。由于设计的机械手关节类型为转动关节，且关节轴1垂直于其余3个关节轴，因此表中参数di为0。参数αi除了α1为90°外，其余都为0；θ1～4后面括号内为各关节角度取值范围，L1～4后面括号内为连杆长度值。

手指相邻连杆之间的坐标变换关系，通过齐次坐标变换矩阵Ai表示，如式(1)所示：

(1)

将表1中的相应参数代入式(1)中,可得手指相邻连杆之间的变换矩阵：

式中：A1表示连杆1相对于基坐标系的变换矩阵；A2表示连杆2相对于连杆1的变换矩阵；A3和A4依次类推。将各个变换矩阵依次连乘，即可获得手指指尖相对于基坐标系的位姿矩阵，如式(2)所示：

T4=A1·A2·A3·A4=

(2)

式中：s1代表sinθ1；c1代表cosθ1；sijkl代表sin(θi+θj+θk+θl)；cijkl代表cos(θi+θj+θk+θl)；i,j,k,l=1,2,3,4。

式(2)中，位姿矩阵T4的左上方3×3矩阵表示手指指尖在基坐标系中的姿态，右上方3×1矩阵表示手指指尖在基坐标系中的位置，如果已知手指指尖在空间中某点的位置坐标点，即可进行逆运动学求解，得到所对应的关节量，通过关节角即可控制手指运动到指定位置点。

2 织物抓取规划的实现

2.1 抓取规划设计

多指机械手是一个复杂的系统，其抓取规划涉及到运动学、动力学、抓取稳定性、抓取接触类型等各个方面[11-12]。本文设计的机械手抓取规划总体结构如图2所示。传感器将织物的物理信息、位置信息及抓取操作的任务要求分给任务分派系统，任务分派系统将这些信息进行分类并分派给相应的规划子系统。位置信息传给调整接近距离系统；几何信息和任务要求信息传给抓取模式规划系统；所抓取织物的质量信息将会被传给抓取力的规划系统，同时此系统还接收到抓取点规划的信息，通过这些系统的协调工作，最终实现对织物的自主抓取操作[13]。

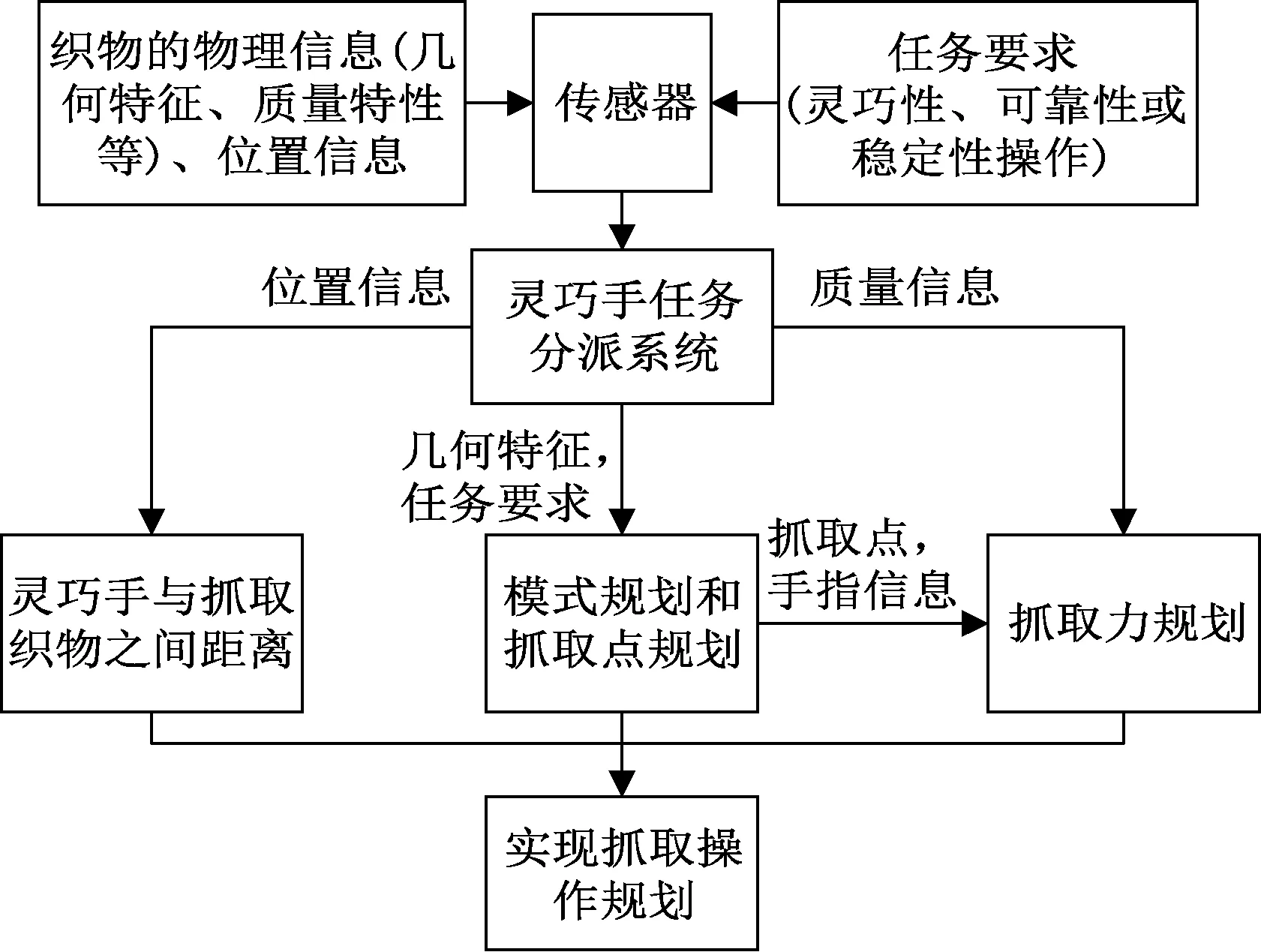
图2 机械手抓取规划结构图Fig.2 Structure chart of dexterous hand grasp planning

2.2 抓取模式规划

对抓取规划进行设计后将进行织物抓取规划的具体分析，主要包括抓取模式规划器设计、织物几何特征描述及提取、抓取任务要求描述、抓取模式模型建立、抓取点规划。

2.2.1 抓取模式规划器设计

本文在研究织物抓取模式分类规划中，着重在于如何通过识别织物的几何特征并根据抓取任务要求建立抓取模式模型，因此，这里不考虑手指与织物之间的接触力和织物所受外力之间的关系，只考虑织物的物理特征和抓取任务要求。通过识别织物的几何特征并根据抓取的任务要求，建立抓取模式模型，以此来对织物进行分类，最终通过机械手实现对织物的抓取操作。

2.2.2 织物几何特征描述及提取

对于柔软织物而言，其在三维空间中有多种姿态，这里先将织物分为平整和非平整2种姿态，以便于描述其几何特征，以毛巾和布片为例，其姿态示意图如图3所示。定义织物的空间长、宽、高分别为l、w、h，并将其作为织物的几何特征。

图3 织物几何特征Fig.3 Fabric′s geometric featurs. (a) Ordered towel; (b) Ordered fabric; (c) Unordered towel; (d) Unordered fabric

根据人手抓取物体的经验，抓取点一般选在比较容易抓取的地方，因此，对于平整的织物，抓取点选择为任意一个边角；对于不平整的织物，选取其垂直方向高度最高的一个点作为抓取点。织物抓取点的高度由传感器获取，并记为h，h值传送给控制器，控制器根据所设计的机械手手指长度d与h值的大小关系，确定抓取模式。

2.2.3 抓取任务要求描述

机械手的抓取姿态包括指面抓取和指侧面抓取。根据所抓取织物的特点将这2种方式均考虑进去，将织物抓取任务信息划分为指面接触抓取(Pinch)和包裹接触抓取(Wrap)。指面接触抓取操作灵活，稳定性稍差；包裹接触抓取稳定性好，不利于灵巧性操作。

2.2.4 抓取模式模型建立

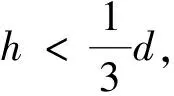
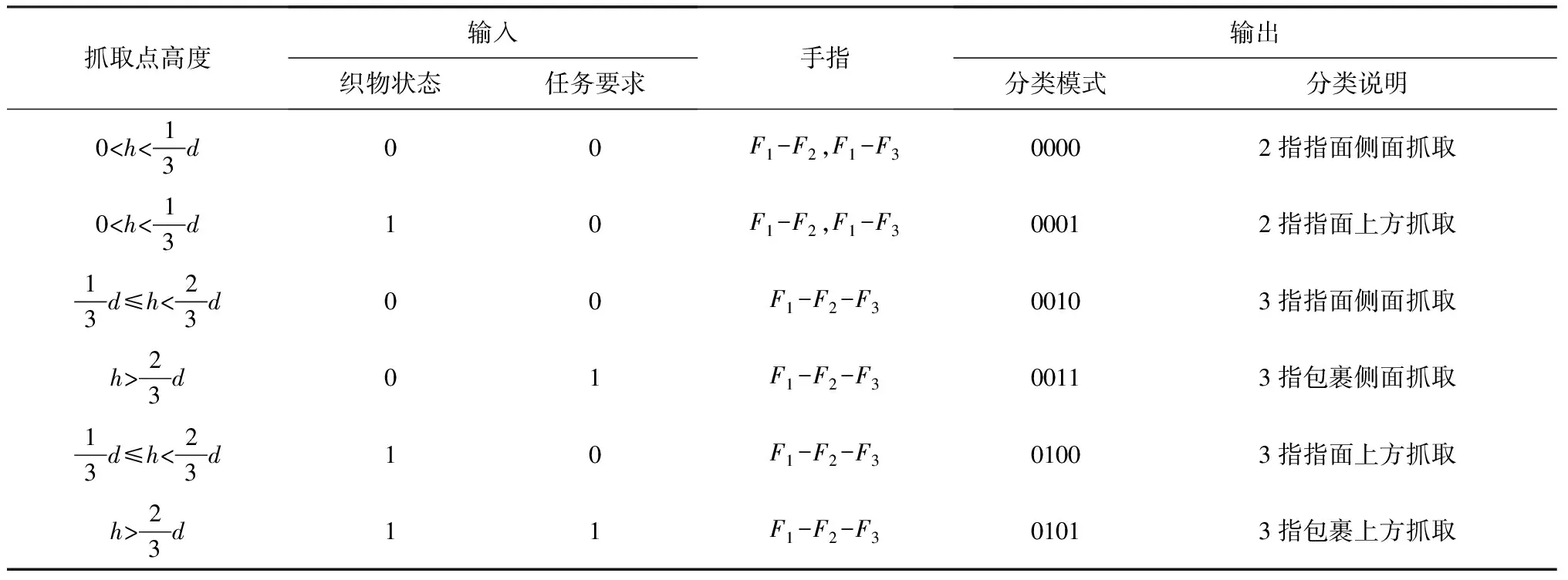
表2 织物抓取模式分类说明表Tab.2 Classification instruction of fabric grasp modes

2.2.5 抓取点规划

所设计的机械手有2指抓取和3指抓取2种方式，要实现稳定可靠的抓取，其抓取接触点的确定原则为：若采用2指抓取，则接触点在过质心的一条直线上；若采用3指抓取，则各手指接触力矢量需要在同一抓取平面上，并且手指接触力的矢量与物体表面垂直，但由于这些点组成的是一个空间平面，为了便于研究，将三维织物抓取点规划简化到二维平面上，这里提出特征平面概念。

特征平面:由至少2条相交或相反的物体表面法向量构成的平面。

通过以上定义可知，3指抓取点的位置落在特征平面的轮廓上，将轮廓分为3等份，确定每个手指抓取接触点，其抓取点位置示意图如图4所示，分别表示2指抓取点和3指抓取点。

图4 抓取点位置图Fig.4 Location schematic of grasp point. (a) Two fingers′ grasp point; (b) Three fingers′ grasp point

3 抓取模式规划的算法实现

RBF神经网络由输入层、隐含层和输出层组成，各层节点数分别用m，q，n表示，其结构如图5所示。RBF神经网络的本质是将输入数据从一个空间转换到另一个空间，这个过程通过隐含层的激活函数来实现，因此在构建RBF神经网络进行织物抓取模式规划时，关键是生成隐含层(将织物信息进行空间转换)，并确定隐含层与输出层之间的权值ωik(将织物信息进行分类处理)。这里选用高斯函数作为隐含层的径向基函数。

图5 RBF神经网络结构图Fig.5 Structure chart of RBF neural network

所选用的高斯函数表达式为

φi(x-ci)=

(3)

式中：φi为隐含层第i个单元的输出；x为输入矢量；ci为隐含层第i个高斯单元的中心；σi为半径。

选择隐含层的径向基函数后，求解其中的参数ci和σi，这里采用K-means聚类算法计算中心ci。选择q个初始聚类中心向量，将所有的样本按最近的聚类中心分组，此算法的准则是从聚类集中的每个样本到聚类中心的距离平方和最小；获得聚类中心ci后，即可计算出半径σi：

(4)

式中，Li是属于第i聚类的数据数。

通过上述计算，即可确定隐含层函数，进而求出RBF神经网络的输出。RBF神经网络第k个输出节点的输出为隐含层各节点输出的线性加权和，计算如下：

φi(x-ci),k=1,2,…,n

(5)

式中：q为隐含层的神经元个数；ωik为隐含层i神经元和输出层k神经元之间的权值；权值ωik通过神经网络的隐含层输出和输出层输出来确定；函数φi(x-ci)的作用是将织物信息进行空间转换，由权值ωik将信息进行分类处理；yk(x)表示输出织物抓取模式规划数据。

经过式(5)确定了RBF神经网络的输出，最后只需确定权值ωik即可完成RBF神经网络抓取模式规划算法。RBF神经网络的隐含层输出、权值和输出层输出之间的关系可以用矩阵表示成如下形式：

(6)

即可表示为

φ·ωik=yk(x)

(7)

式中，j为每个输入包含部分的个数。

由式(7)可得：

ωik=φ-1·yk(x)=(φTφ)-1·yk(x)

(8)

通过式(8)即可根据现有数据确定隐含层和输出层之间的权值ωik，当给出1组新的输入数据，即可由式(5)求出所对应的输出。在机械手进行织物抓取时，RBF神经网络能够快速地对环境进行学习，提取织物的几何特征并根据任务要求对抓取织物进行分类，计算机获取其输出的抓取模式分类数据后通过控制器控制机械手完成抓取操作。

4 抓取运动轨迹规划

4.1 轨迹规划方法的选择

机械手抓取模式规划完成后，通过计算机控制，从初始位置运动到目标位置进行织物抓取操作，这个过程需要进行运动学轨迹规划。为了使抓取更加合理准确，本文采用关节空间和笛卡尔空间相结合的轨迹规划方式[14]。从初始位置点到靠近位置点，对路径没有特殊的要求，因此，采用关节空间中的多项式轨迹规划。从靠近位置点到接触位置点，对路径有要求，不仅要考虑机械手的每个手指是否同时到达目标点，而且还要考虑抓取力的问题，因此，采用笛卡尔空间的轨迹规划。

4.2 五次多项式规划

五次多项式既可满足运动过程中加速度要求，又可兼顾运行时间和使用负载，因而采用五次多项式进行关节空间中轨迹规划。机械手各关节在起点和终点的位置、速度和加速度的约束条件为

θ(t0)=θ0;θ(td)=θd;

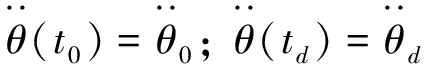
(9)

由式(9)约束条件可以确定一个唯一的五次多项式：

θ(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5

(10)

对式(10)求一阶和二阶导数，可得：

(11)

联立式(9)～(11)，整理可得：

(12)

式(12)就是关节的轨迹函数，它确定了手指运动过程中任意时刻的关节位置，通过各个关节的运动即可拟合出手指指尖的运动。由式(12)还可得到关节的速度和加速度公式，如式(14)所示,通过速度和加速度函数可反映出手指的运动情况。

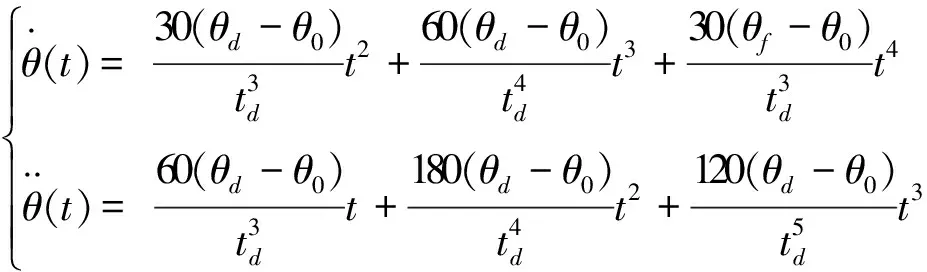
(13)

4.3 直线插补规划

从靠近点到接触点的轨迹规划采用笛卡尔空间中的直线插补方法，该方法是在已知直线始末两点位姿的前提下，求直线轨迹上各个插补点的位置和姿态。如图6所示，设始末两点位姿分别为P1、P2。

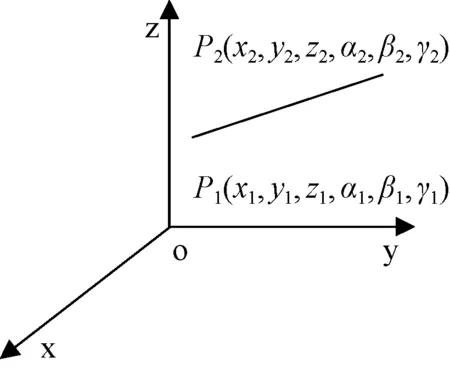
图6 空间直线插补Fig.6 Space linear interpolation

插补点的位置和姿态坐标点的值求解如下：

(14)

式中：(x1,y1,z1)、(α1,β1,γ1)分别为起始点的位置和姿态角；(x,y,z)、(α,β,γ)分别为插补点的位置和姿态角；λ为归一化因子；(△x,△y,△z,△α,△β,△γ)为位置和姿态角的增量，其求解如下：

(15)

式中，(x2,y2,z2)、(α2,β2,γ2)分别为接触点的位置和姿态角。

λ主要采用抛物线过渡的线性函数，这样能够保证整条轨迹上的位移和速度都连续。求出λ后即可确定插值点，设抛物线过渡的线性函数的直线段速度为ν，抛物线段的加速度为A。则抛物线段的运动时间Tb和位移Lb分别为

(16)

(17)

直线的长度L和运动的时间T分别为

(18)

(19)

抛物线段位移、时间、加速度分别归一化处理：

(20)

则可得出λ的计算公式：

(21)

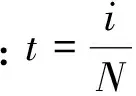
5 仿真实验

利用MatLab/Robotics Toolbox中提供的机器人函数进行机械手织物抓取规划建模仿真。首先结合前面机械手的结构设计和运动学分析，建立机械手的空间三维结构模型。设3个手指的初始点关节量分别为q1=[0.523 6000]、q2=[2.6170000]、q3=[-π/2000]，通过调用函数编程，即可建立三指机械手初始点位置的空间三维模型，如图7所示。

图7 机械手初始点位置三维模型Fig.7 3 D model of dexterous hand’s initial point location

建立机械手的三维模型后，根据前面的抓取规划要求和运动轨迹规划，即可实现机械手的抓取操作运动过程仿真，如图8所示。其中点M1、M2、M3分别为3个手指的初始位置点，对应于图7所示位置，点P为接触点，N1、N2、N3分别为各手指靠近点位置，从点M到点N的红绿蓝3条曲线M1N1、M2N2、M3N3分别为手指1、手指2、手指3在关节空间中五次多项式规划的运动轨迹，从点N到点P的3条洋红色直线N1P、N2P、N3P分别为手指1、手指2、手指3在笛卡尔空间中直线规划的运动轨迹，从图中可看出各手指轨迹达到了预期的要求，但这些还不能说明设计的机械手就是稳定可靠的。由于机械手在抓取的过程中，不仅要保证每个手指在指定的工作空间范围内运动，而且还要保证每个手指都能够同时到达目标点，满足作用力要求，因此，需要对其操作空间和指尖位移进行仿真分析。

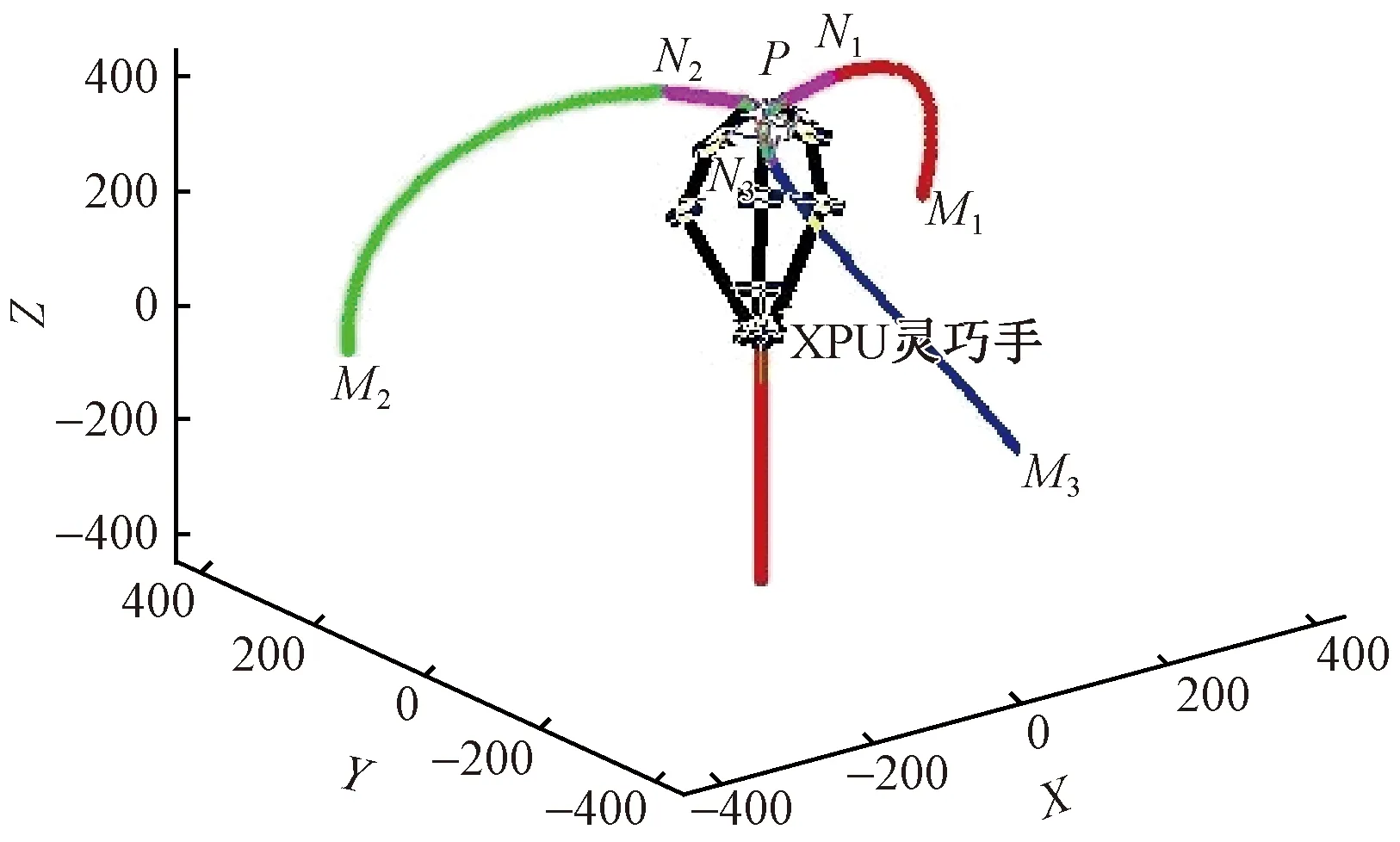
图8 灵巧手抓取运动规划图Fig.8 Planning chart of dexterous hand grasp movement

图9示出手指的三维工作空间示意图。红色部分表示手指的工作区域，在这个工作空间范围内手指能到达任意一点。

图10示出各手指指尖点位移图。可以看到各手指运动正常，没有发生错位突变的情况，表明织物抓取过程稳定可靠。

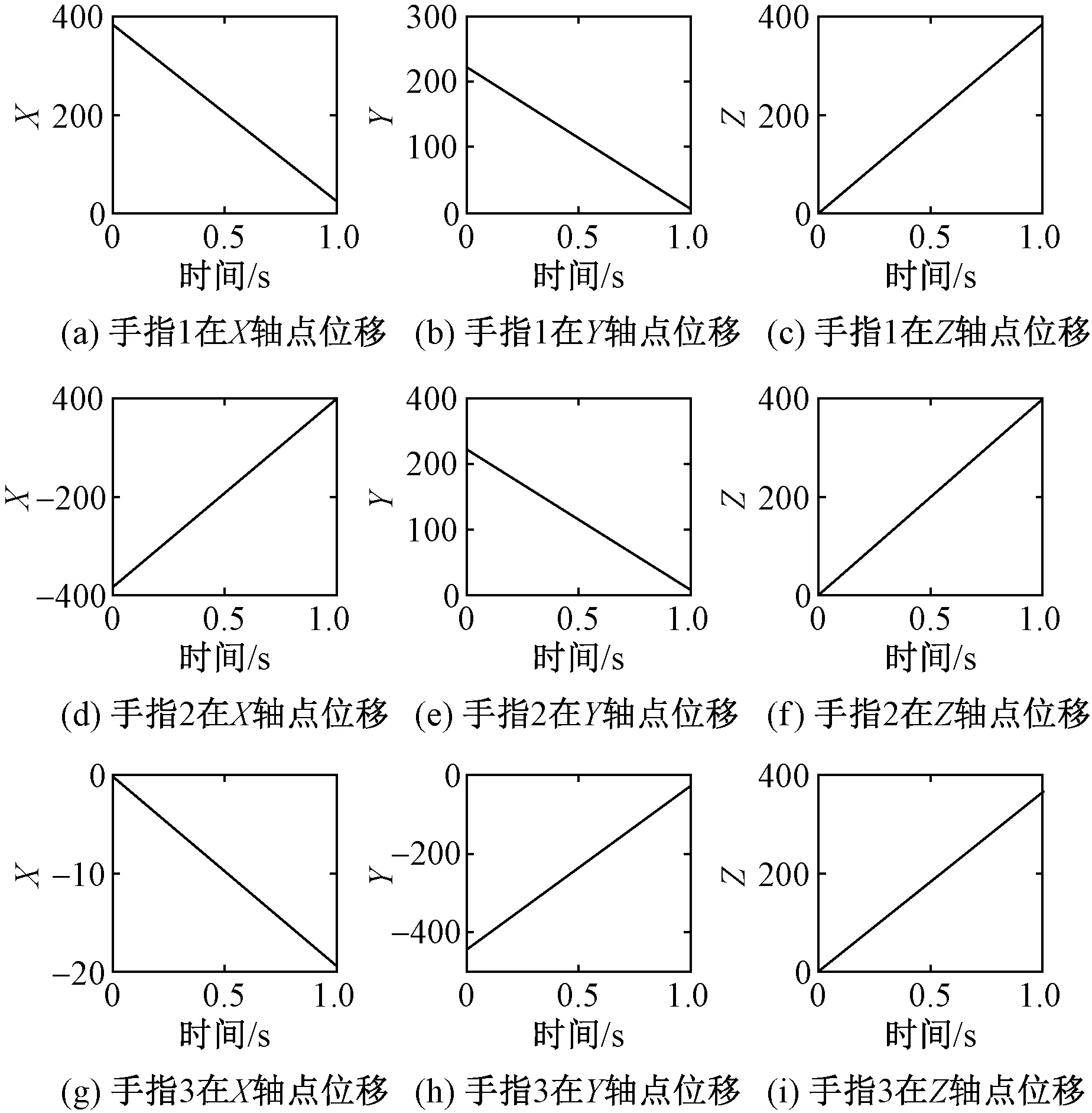
图10 手指指尖点位移图Fig.10 Drawing of fingers′ point displacement. (a) Finger 1 in X-axis point displacement; (b) Finger 1 in Y-axis point displacement; (c) Finger 1 in Z-axis point displacement; (d) Finger 2 in X-axis point displacement; (e) Finger 2 in Y-axis point displacement; (f) Finger 2 in Z-axis point displacement; (g) Finger 3 in X-axis point displacement; (h) Finger 3 in Y-axis point displacement; (i) Finger 3 in Z-axis point displacement

6 结 语

本文针对纺织服装行业织物抓取问题进行研究，设计了3指机械手并进行了运动学分析，然后根据织物的几何特征和抓取任务要求，选取以高斯函数作为径向基函数的RBF神经网络方法对其进行抓取模式规划，并采用关节空间和笛卡尔空间混合的方式进行运动轨迹规划，最后通过仿真实验进行验证。结果表明，多指机械手结构设计合理，关节参数设置满足抓取要求，织物抓取规划方法准确可靠。本文研究为多指机械手织物抓取研究分析，以及在纺织服装行业织物抓取操作的应用提供了理论依据。FZXB

[1] 高利斌,郭冰菁,王凯.仿人机械手的结构设计与单指的控制策略[J].液压与气动, 2012(2): 11-14. GAO Libin, GUO Bingjing, WANG Kai. Dexterous robot fingers structural design and single-finger control stategy[J]. Chinese Hydraulics and Pneumatics, 2012(2):11-14.

[2] 张延恒,贠超,孙汉旭,等.对称结构三指机械手抓持规划[J].机床与液压, 2007, 35(9): 76-78. ZHANG Yanheng, YUN Chao, SUN Hanxu,et al. Grasp planning for three fingered hands with symmetrical configuration[J]. Machine Tool and Hydraulics, 2007,35(9):76-78.

[3] 杨永.用于采摘机器人的空间定位方法及试验[J].制造业自动化, 2014(23): 49-52. YANG Yong. The space locating method and experiments for picking robot[J]. Manufacturing Automation, 2014(23):49-52.

[4] 陈兆芃,金明河,樊绍巍,等.面向任务的机器人机械手控制系统及多指空间协调阻抗控制[J].哈尔滨工程大学学报, 2012, 33(4): 476-484. CHEN Zhaopeng, JIN Minghe, FAN Shaowei, et al. The task-oriented control system of a dexterous robot hand with a multi-fingered spatial coordinating impedance control[J]. Journal of Harbin Engineering University, 2012,33(4):476-484.

[5] 张敏,王鸿博,高卫东,等.喷气织机车速对织物纬向物理力学性能的影响[J].纺织学报, 2016, 37(8): 41-46. ZHANG Min, WANG Hongbo, GAO Weidong,et al. Influence of air-jet loom speed on weft physical and mechanical properties of fabrics[J]. Journal of Textile Research, 2016,37(8):41-46.

[6] 田景山,王文敏,王聪,等.机械采收方式对新疆棉品质的影响[J].纺织学报, 2016, 37(7): 13-17. TIAN Jingshan, WANG Wenmin, WANG Cong,et al. Effect of cotton mechanical picking on fiber qualities in Xinjiang[J]. Journal of Textile Research, 2016,37(7):13-17.

[7] 张昭昭,乔俊飞.基于在线减法聚类的RBF神经网络结构设计[J].控制与决策, 2012, 27(7): 997-1002. ZHANG Zhaozhao, QIAO Junfei. Design RBF neural network architecture based on online subtractive clustering[J]. Control and Decision, 2012,27(7):997-1002.

[8] 姜莹礁,赵怀勋,贾琪,等.基于聚类RBF神经网络的人体行为识别[J].计算机应用与软件, 2013, 30(2): 47-49. JIANG Yingjiao, ZHAO Huaixun, JIA Qi, et al. Human behavior recognition using clustering method and RBF neural metwork[J]. Computer Applications and Software, 2013,30(2):47-49.

[9] 赵雪.机织物接缝强力测量的不确定度分析[J].纺织学报, 2015, 36(10): 49-53. ZHAO Xue. Discussion on uncertainty in seam strength measurement of woven fabric[J]. Journal of Textile Research, 2015,36(10):49-53.

[10] 赵立环,张杰.织物折皱回复角与其力学性能指标间的关系[J].纺织学报, 2013, 34(10): 39-42. ZHAO Lihuan, ZHANG Jie. Relationship between fabric′s wrinkle recovery angle and its mechanical properties[J]. Journal of Textile Research, 2013, 34(10):39-42.

[11] LIN G D, LI Z J, LIU L, et al. Development of multi-fingered dexterous hand for grasping manipulation[J]. Sciece China Information Sciences, 2014,57(12):1-10.

[12] WANG Z H, ZHANG L B, BAO G J, et al. Design and control of integrated pneumatic dexterous robot finger[J]. Journal of Central South University of Technology, 2011,18(4):1105-1114.

[13] 陆志远,甘亚辉,戴先中,等.基于似人特性的拟人臂机器人自主抓取动作规划[J].机器人, 2014, 36(6): 719-729. LU Zhiyuan, GAN Yahui, DAI Xianzhong, et al. Autonomous grasp motion planning for an anthropomorphic robot arm based on human like-ness[J]. Robot, 2014,36(6):719-729.

[14] 郭超,辛世界,李玉胜.两种坐标空间中Delta机器人轨迹规划仿真[J].制造业自动化, 2014(4): 49-51. GUO Chao, XIN Shijie, LI Yusheng. Simulation of Delta robot trajectory planning in two kings of coordinate space[J]. Manufacturing Automation, 2014(4):49-51.

Fabric grasp planning for multi-fingered dexterous hand based on neural network algorithm

ZHANG Lei, WEI Pandong, LI Pengfei, WANG Xiaohua, LIU Xiuping

(SchoolofElectronicsandInformation,Xi′anPolytechnicUniversity,Xi′an,Shaanxi710048,China)

For fabric autonomous grasp of textile and garment industry, low production efficiency will be caused by manual operation. Fabric is grasped by dexterous hand in this paper. Firstly, multi-fingered dexterous hand was designed and a method of kinematics analysis was used by describing coordinates transformation relation of fingers′ connecting rod. Grasp mode planning was programmed by using Radial Basis Function (RBF) neural network method. By identifying the fabric′s geometric feature and according to the requirements of the grasp tasks autonomous grasp is realized. In the process of grasp movement, the joint space trajectory planning and Cartesian space trajectory planning were combined to ensure the dexterous hand fingers can stably and accurately reach to the grasp point. Finally, multi-fingered dexterous hand and grasp planning were simulated by using MatLab/Robotics Toolbox, and the simulation results show that the design of the dexterous hand joint parameters setting is reasonable, and fabric grasp planning meets the requirements.

multi-fingered dexterous hand; grasp mode planning; RBF neural network; trajectory planning; fabric grasp

10.13475/j.fzxb.20160105008

2016-01-22

2016-09-02

陕西省教育厅科研计划项目资助项目(14JK1306)；陕西省科技计划项目(2016GY-136)；西安工程大学学科建设经费资助项目(107090811)

张蕾(1981—)，女，讲师，博士。研究方向为机器人运动控制、非线性控制理论分析。E-mail:11795503@qq.com。

TP 241； TS 103.8

A