一题多证 放飞思维
2017-05-17 09:56:02江西省信丰中学341600赖学锋
数理化解题研究 2017年10期
江西省信丰中学(341600) 赖学锋●
一题多证 放飞思维
江西省信丰中学(341600)
赖学锋●

证法一:综合法
∵(a+2)2+(b+2)2=a2+b2+4(a+b)+8=a2+b2+12,
又∵a2+b2=(a+b)2-2ab=1-2ab,
∴(a+2)2+(b+2)2=13-2ab.


证法二:分析法

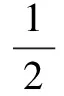
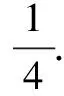

∴原不等式得证.
证法三:比较法

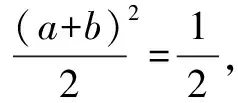


则原不等式成立.
证法四:代数换元法


∴原不等式得证.
证法五:利用基本不等式变形

∵(a+2)2+(b+2)2


证法六:构造函数法
令y=(a+2)2+(b+2)2,
∵a+b=1,


∴原不等式得证.
证法七:几何法
∵a+b=1,
∴点(a,b)在直线l:x+y-1=0上.
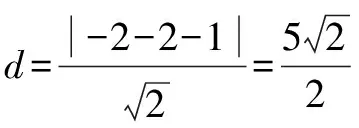
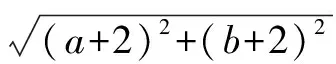

证法八:反证法
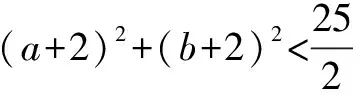




∴假设错误,原命题成立.
G632
B
1008-0333(2017)10-0041-01
猜你喜欢
印制电路信息(2024年1期)2024-03-13 23:57:50
中等数学(2022年7期)2022-10-24 01:47:20
新世纪智能(数学备考)(2021年4期)2021-08-06 09:04:40
艺术大观(2020年11期)2020-10-09 10:05:21
建材发展导向(2019年11期)2019-08-24 06:34:54
——信丰阁
城乡建设(2019年14期)2019-02-20 02:08:31
中央民族大学学报(自然科学版)(2018年1期)2018-06-27 01:27:40
现代园艺(2018年1期)2018-03-15 07:56:14
中学生数理化·高一版(2017年9期)2017-12-19 12:15:14
中学生理科应试(2017年2期)2017-04-01 21:03:31

