大兴安岭地区天然兴安落叶松疏开木冠幅预测模型1

张树森，贾炜玮，王玉霞，高慧淋

(1.黑龙江省尚志国有林场管理局，黑龙江 尚志 150600；2.东北林业大学 林学院 哈尔滨 150040)

大兴安岭地区天然兴安落叶松疏开木冠幅预测模型1

张树森1，贾炜玮2*，王玉霞2，高慧淋2

(1.黑龙江省尚志国有林场管理局，黑龙江 尚志 150600；2.东北林业大学 林学院 哈尔滨 150040)

基于2016年大兴安岭地区十个林业局的天然兴安落叶松林样地调查数据，实测样地内疏开木的胸径与东、西、南、北四个方向的冠幅。分析疏开木胸径与冠幅之间的关系，采用线性模型和非线性模型作为备选模型，分别构建了天然落叶松的冠幅预测模型，经过拟合优度指标与检验结果进行最优模型的选取。将所有树木按照胸径的变化范围分为3个等级(即DBH≤20 cm、20 cm40 cm)，基于选取的最优冠幅预测模型，采用哑变量的方法同时构建了3个等级天然兴安落叶松疏开木冠幅的通用模型，并进一步分析3个等级冠幅模型之间的差别。结果表明：线性模型和非线性模型均能够很好的拟合天然兴安落叶松疏开木的冠幅模型，由拟合优度和检验指标最终选取非线性模型作为基础模型。利用哑变量构建的3个等级疏开木冠幅的通用模型为CW=(0.353 3G1+0.225 5G2+1.537 6G3)DBH(0.587 5G1+0.738 5G2+0.190 4G3)。其中，DBH≤20 cm、20cm40 cm的两个系数则没有通过t检验。

天然兴安落叶松林；冠幅预测模型；哑变量；大兴安岭地区

0 引言

在森林生态系统中，冠层是森林与外界环境进行相互作用最为直接的部分，同时也是林木进行营养循环的重要场所。树冠能很好的反应树木的长期竞争水平，林木通过树冠进行光合作用和呼吸作用，产生并积累能量，供林木进行呼吸作用。树冠通过林冠截留不仅能为林木的生长提供大量的水分，而且还能减缓雨水对地面的冲刷，防止水土流失。人们通常用材积三要素(形数、断面积、树高)计算林木材积，从而评价林木的经济价值。断面积的大小与林木树冠的大小有着密不可分的关系。人们常用枝繁叶茂来评价一株林木的生长状态。一般来说，同一立地条件下，同种林木、相同年龄，枝叶越茂密，冠幅值越大，林木生长就越好，获得的单木经济价值就越高。树木在生长的过程中，如果遇到自然灾害或者人为干扰，最先发现变化的是树冠的变化，接着才会发现树木的冠长、叶面积、树冠表面积等也会发生变化。相比较而言，冠幅测量方法简单、操作方便，而叶面积、树冠表面积等需要大量的测量与计算，费时费力，比较麻烦。因此，人们通常用树冠的大小来评价树木是否生长健康，以及林木质量的优劣。胸径和冠幅都是用来描述树冠生长的重要指标，冠幅不但可以用来计算树木的竞争指数，而且可以预测树高或胸径生长量等。

树冠研究指标一般分为两种，一种是冠幅、叶面积指数等能够直接测定的指标，另外一种是疏透度、圆满度、树冠率、树冠竞争因子(CCF)等需要间接计算的指标。其中人们最常用的是冠幅指标，其次是树冠竞争因子指标。在许多森林经营管理中，树冠指标常常被用来作为制定营林决策的重要依据之一。大量研究表明，冠幅与胸径有着明显的相关关系。Curtis等是第一个使用线性回归法，构建黄杉(Pseudotsugamenziesii(Mirb.)Franco)冠幅生长模型[1]。构建单木冠幅模型的方法相对比较多，但是线性回归模型比较多[2-4]。国内外学者对单木冠幅模型进行了大量研究。例如，唐守正为了计算树冠竞争因子(CCF)，使用线性模型、幂函数和双曲线函数模型来拟合杉木(Cunninghamialanceolata(Lamb.)Hook)和长白落叶松(LarixolgensisHerry)疏开木与胸径关系模型，发现双曲线函数模型效果略好一些[5]。符亚健等考虑单木冠长、每公顷株数和林木竞争压力指数等因子，从9个常见的冠幅-直径备选模型中选出一个拟合精度较高的三参数的逻辑斯蒂形式的冠幅-直径模型作为构建华北落叶松(Larixprincipis-rupprechtiiMayr)单木冠幅模型的基础模型，从而更好地模拟当地华北落叶松冠幅与胸径的关系[6]。自21世纪初以来，对树木冠幅的研究得到广泛的重视，迄今为止，针对冠幅模型的构建已提出了多种建模方法，例如，Gill等利用加权最小二乘法拟合模型，构建加利福尼亚几种针叶树种树冠半径模型[7]。雷向东等利用SPSS软件，采用逐步回归分析法选取所需自变量，采用多元回归模型建立了长白落叶松、冷杉(Abiesnephrolepis)、红松(Pinuskoraiensis)、云杉(Piceakoraiensis)等9个树种的冠幅预测模型[8]。符利勇等以湖南省黄丰桥国有林场调查的杉木为研究对象，把立地指数和嵌套在立地指数中的样地作为随机效应因子，利用2水平非线性混合效应模型构建混合效应模型单木冠幅预测模型[9]。

兴安落叶松(Larixgmelinii(Rupr.)Kuzen)，为松科、落叶松属的落叶乔木，是中国东北林区的主要森林树种，是大兴安岭优良的乡土树种，同时也是大兴安岭原始森林的主要组成树种，主要分布于大、小兴安岭，苏联远东地区也有分布。兴安落叶松喜光性强，在各种不同环境均能生长，常组成大面积的单纯林，兴安落叶松木材蓄积丰富，也是东北地区进行荒山造林和更新的主要树种。兴安落叶松木材略重，硬度中等，易裂，边材淡黄色，心材黄褐色至红褐色，纹理直，结构细密，相对密度为0.32～0.52，有树脂，耐久用等特点，可供房屋建筑、土木工程、电杆、舟车、细木加工及木纤维工业原料等用材，树干可提取树脂，树皮可提取栲胶，是东北地区的主要速生丰产林木，也是我国重要的用材树种。本次研究根据大兴安岭地区天然落叶松疏开木的胸径与冠幅之间的关系，通过拟合与检验，构建以胸径作为单一变量来预测冠幅的大小的模型。将树木按照胸径大小分为3个等级，即DBH≤20 cm，20 cm40 cm，采用哑变量的方法构建了天然落叶松疏开木3个等级冠幅的通用模型，并对3个等级的冠幅进行了比较，以期为今后大兴安岭地区森林可持续经营提供科学依据。

1 研究地区概况数据收集

1.1 研究地概况

大兴安岭地区地处我国最北部边陲，东与小兴安岭毗邻，西以大兴安岭山脉为界与内蒙古自治区接壤，南濒广阔的松嫩平原，北以黑龙江主航道中心线与俄罗斯为邻。大兴安岭地区天然地处黑龙江省西北部，内蒙古自治区东北部，大兴安岭山脉的东北坡，处于根河与嫩江两条地震大断裂带上，是黑龙江省下辖地区，属黑龙江省十三个地级行政单位之一。大兴安岭地区位于东经121°12′到127°00′，东西横跨6个经度，北纬50°10′到53°33′，南北纵越3个纬度，属寒温带气候区，年降水量偏低(大约为350～500 mm)，年平均气温-2～-4 ℃，有的地方极端最低温-52.3 ℃。大兴安岭地区是我国重点国有林区和天然林主要分布区之一，也是中国唯一的寒温带针叶林区和国内仅存的寒温带生物基因库，森林覆盖率79.83%。大兴安岭地区疆域广阔，东西长410 km，南北宽386 km，行政区面积8.46万km2，包括塔河、新林、西林、呼中、加格达奇、松岭、韩家园、十八站、阿木尔和图强十个林业局。

1.2 数据来源

本次研究的数据是来自2016年大兴安岭地区的十个林业局，研究区域内有天然分布的兴安落叶松林。在每一个林业局内选择有地域代表性，体现不同立地条件差异的不同径阶的兴安落叶松疏开木为调查对象，利用胸径尺测量距离地面1.3处的直径，称为胸径(DBH)，胸径范围为3.6～50.2 cm，精确到0.1 cm。利用钢尺以样木为中心，分别对其正东、正西、正南、正北4个方向的最大树冠半径进行测量，精确到0.1 m。统计不同径阶树木的基本信息(表1)。统计东、西、南、北 4 个方向的冠幅半径，求出单木冠幅的平均值，其计算公式为

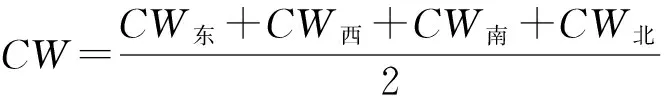
式中：CW东、CW西、CW南、CW北分别代表以样木为中心所测量的东、南、西、北4 个方向的最大树冠半径，CW是指单木冠幅，m。

将所有数据按照3∶1的比例随机的分为拟合样本和检验样本，拟合样本用于模型参数的估计，检验样本用于对模型的预测能力进行评价。

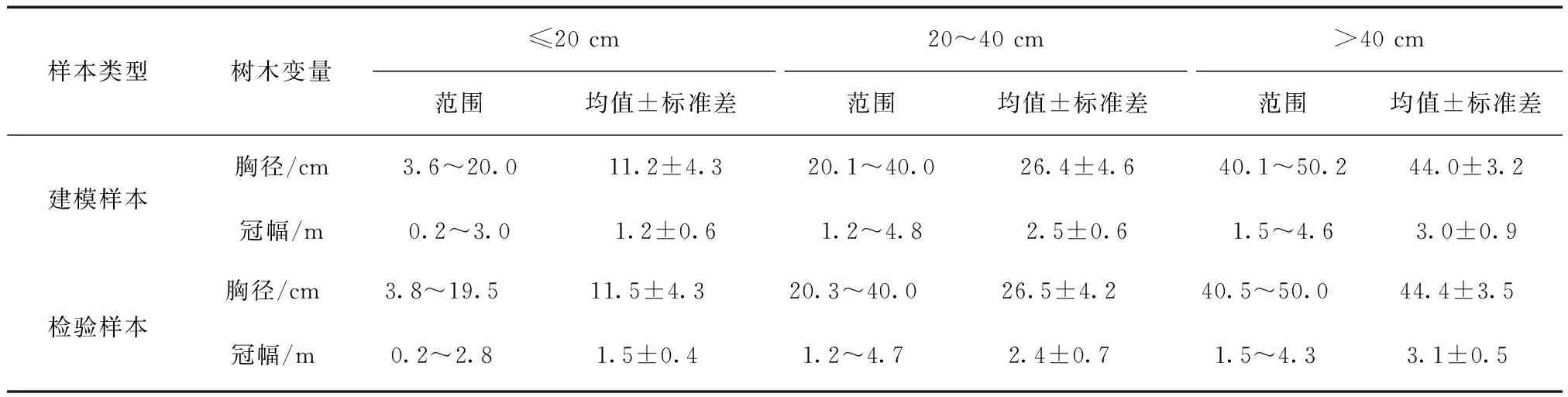
表1 不同径阶树木变量基本信息统计Tab.1 Statistical information for the individual tree variables from different DBH class

2 研究方法

2.1 备选模型的选取

Krajicek等认为冠幅(CW)与胸高直径(DBH)呈线性相关关系[10]。后来研究者发现胸径生长与冠幅大小的相关规律不受立地条件与林龄差异的影响[11]。国内外对冠幅和胸径关系进行了大量的研究，其中有9个常用的冠幅-胸径模型[12-15]，本文选取了几个常用的模型进行了研究和比较。

基于以往研究成果，通过对天然落叶松疏开木胸径(DBH)与冠幅(CW)的关系进行分析，以样木胸径(DBH)为自变量，实测冠幅(CW)为因变量，做DBH-CW的散点图。根据散点图的分布趋势对散点图进行分析，可看出随着DBH的越大，CW也呈现增大的趋势。本文主要构建以下3个备选模型，然后用SAS9.3软件PROC Model模块进行模型的拟合。备选模型的形式如下所示：

CW=a1+a2DBH。

(1)

CW=a1+a2DBH+a3DBH2。

(2)

CW=a2DBHa2。

(3)

式中：CW为单木冠幅，DBH为样木胸径，a1、a2、a3为模型参数。

2.2 基于哑变量的不同等级树木通用冠幅模型的建立

近年来，哑变量模型的研究越来越受到人们的重视。在使用最优模型的基础上，在不增加自变量的前提下，可以使用哑变量方法构建模型，从而提高模型的预测精度，这在以前就有所研究。例如，符利勇等对东北地区兴安落叶松和长白落叶松两个主要树种构建生物量方程时，考虑林分不同起源能提高方程预测，因此把林分起源差异当作固定效应，通过哑变量方法构建不同树种生物量模型方法，增加自变量能提高方程预测效果[16]。

常用哑变量模型方法进行各种回归分析和建模实践[17-19]。哑变量为虚拟变量，哑变量是对定性因子或分类变量进行处理的一种常用方法，一般取值为0 或1。哑变量的定义为：对于等级性(定性)数据x，用变量δ(x，i)表示，当x取值为第i等级时，δ(x，i)=1，否则为0[19]。

2.3 模型拟合及检验指标

利用均方根误差(RMSE)和调整后的决定系数(R2)两个指标对模型的拟合优度进行评价。当R2的值越大，而RMSE的值越小时，说明模型的拟合效果越高，模型愈适用。再分别对模型进行独立性检验，计算指标平均误差(ME)、平均绝对误差(MAE)、平均误差绝对值(MA%E)的值。ME、MAE、MA%E的值越小，说明模型的预测效果越好。各指标计算公式如下：

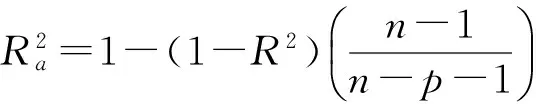
(4)

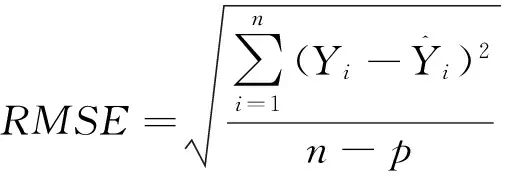
(5)

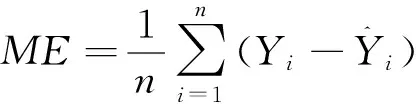
(6)

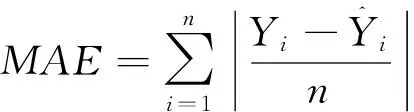
(7)

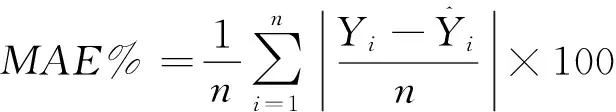
(8)

3 结果

3.1 最优模型的选取

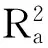
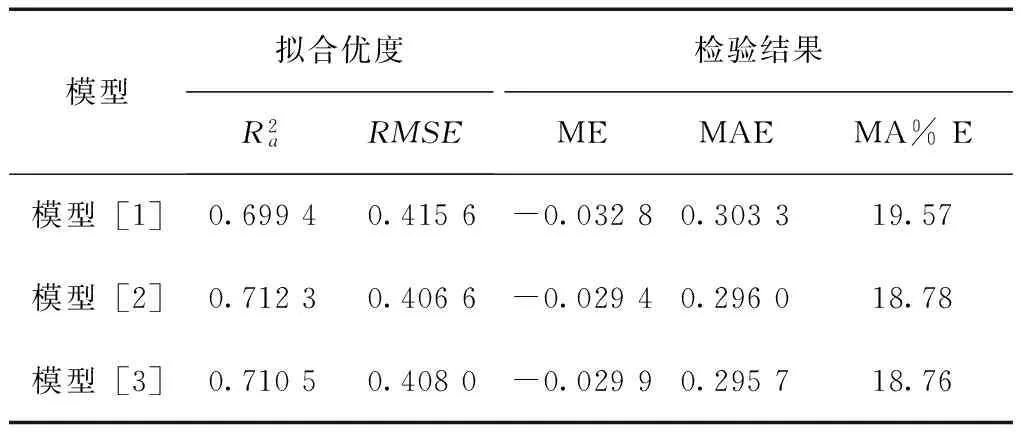
表2 各个备选模型的拟合优度及检验结果比较Tab.2 Goodness-of-fit and validation results for the basic models

3.2 不同径阶的冠幅通用模型的建立

3.2.1 构建哑变量模型

通过对模型进行拟合与检验，得出模型(3)为最优基础模型。本次研究收集的胸径数据，考虑胸径值之间的差异性，将胸径分为0～20 cm、20～40 cm、>40 cm3个径级，将这3个不同的径级带入基础模型中，引入哑变量，将不同径级范围的样木用定性代码表示，从而整合成一个模型来构建。当G1=1、G2=0、G3=0时，代表径阶为0～20c m的冠幅预测模型；当G1=0、G2=1、G3=0时，代表径阶为20～40 cm的冠幅预测模型；当G1=0、G2=0、G3=1时，代表>40 cm径阶。考虑到落叶松的胸径大小不同，预测的冠幅数值可能会存在一定的差异。在所构建的冠幅预测模型的基础上，通过引入哑变量的方法，构建了不同径阶的大兴安岭地区天然落叶松疏开木冠幅的通用模型，模型的具体形式如下所示。

CW=(a1G1+a2G2+a3G4)DBH(b1G1+b2G2+b3G3)。

(9)

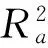
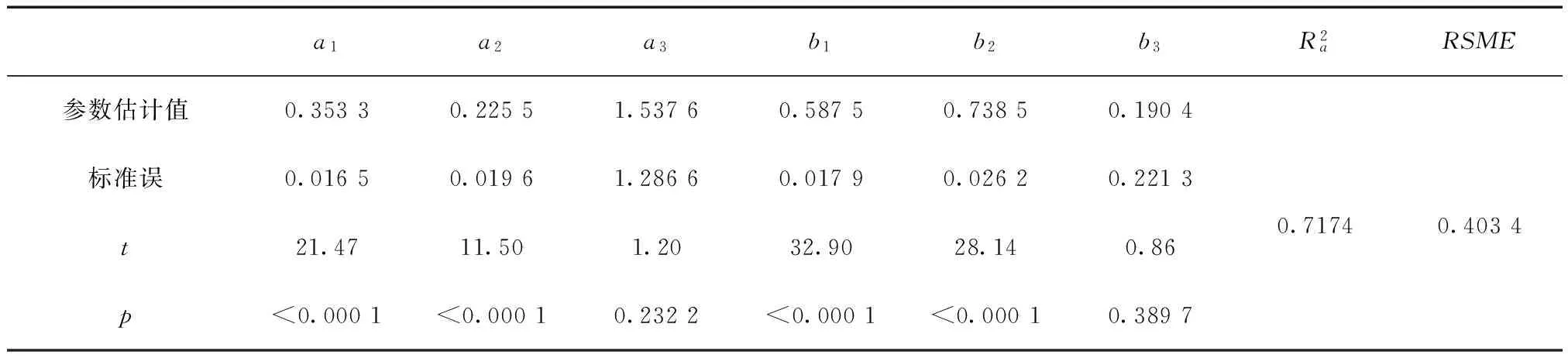
表3 基于哑变量人工落叶松不同径阶大小林木冠幅模型的参数估计结果Tab.3 Estimates for the parameters of the crown width model for the different classes of natural Larix gmelini plantation based on dummy variable

3.2.2 消除异方差，绘制残差图

做各径阶冠幅预测模型的残差图，通过观察模型残差分布图，发现残差值的分布均匀，残差值分布的离散程度有扩大的趋势，表明预测模型存在一定程度的异方差性，因此需要消除异方差，使残差值均匀分布。消除异方差，常用方法有对数回归法和加权回归法[20-23]。本文通过加权的方法消除异方差，得到分布相对均匀的残差分布图(图1)。

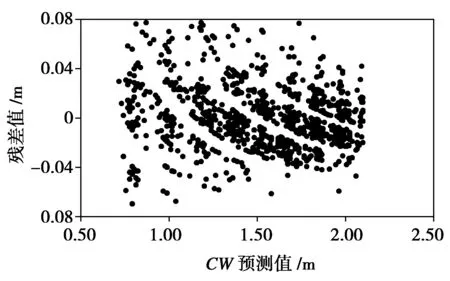
(a)

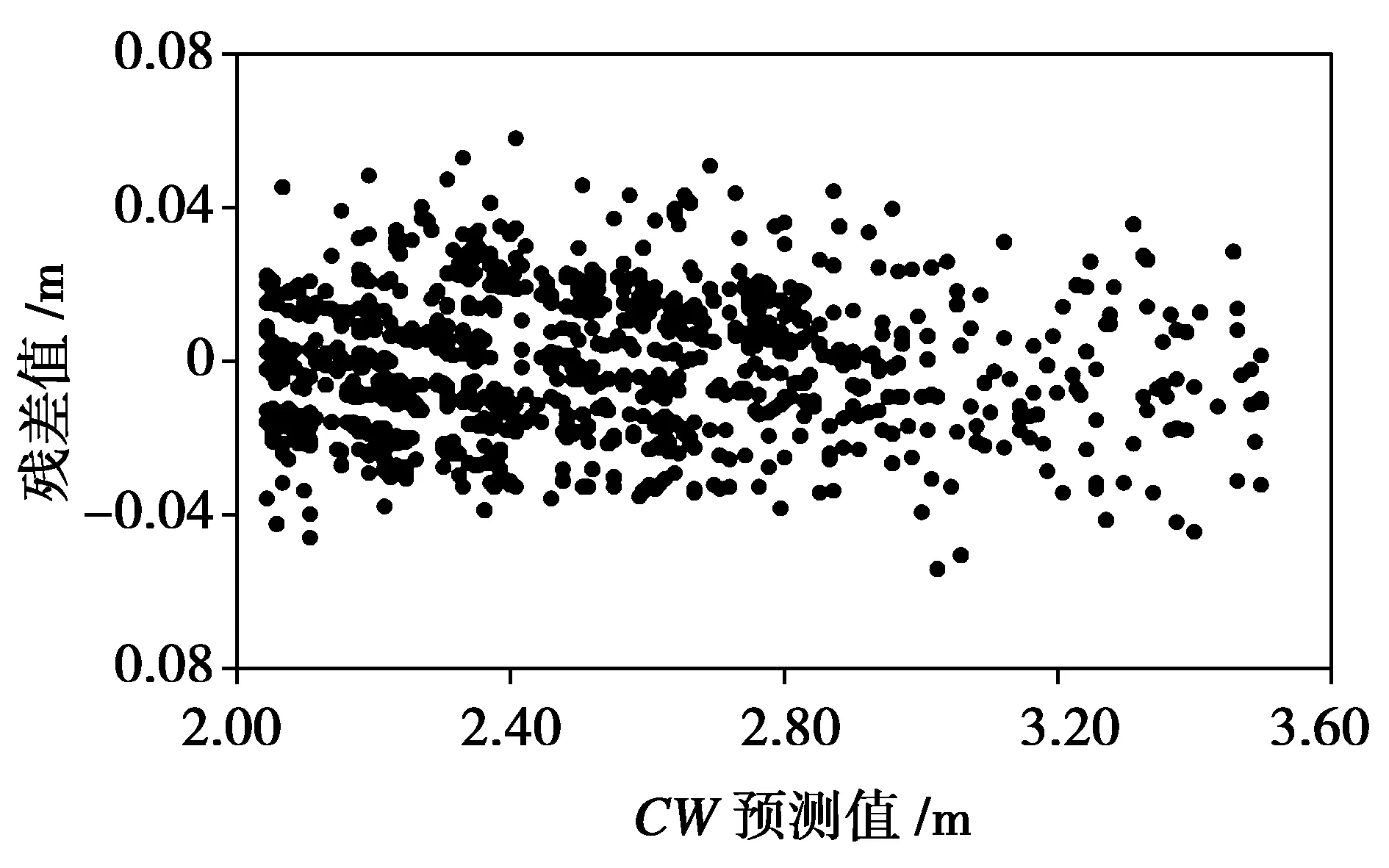
(b)

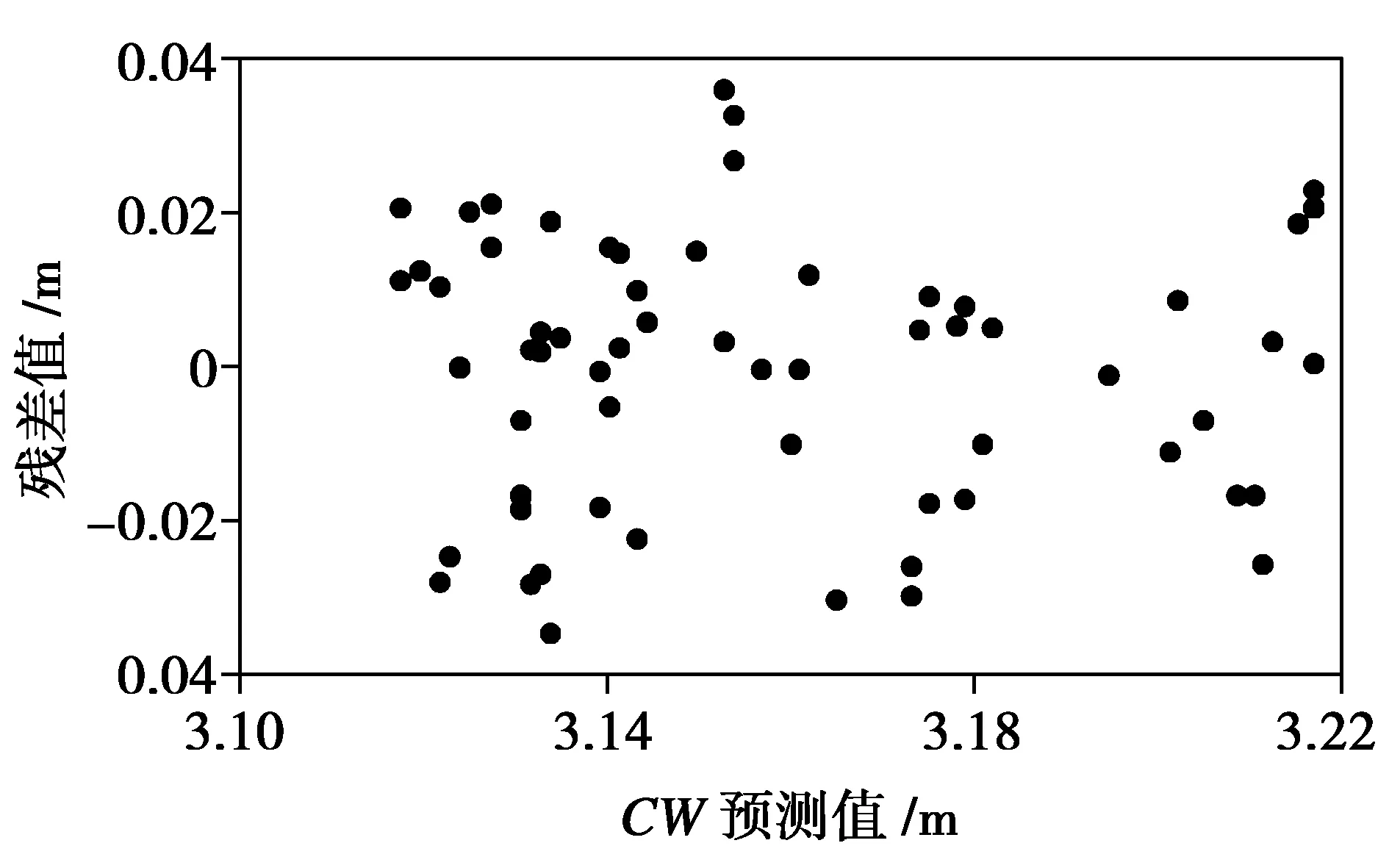
(c)图1 各径阶冠幅预测模型消除异方差后的残差图 (a、b、c分别代表≤20 cm、20 cm<40 cm、>40 cm 3个径阶的残差图)Fig.1 Residual plots for the predicted crown width model of different classes after the eliminating for the heteroscedasticity(a，b，c represents the residual plots for ≤20 cm、20 cm<40 cm、>40 cm，respectively)

4 结论与讨论

本研究是收集了2016年大兴安岭地区十个林业局分布的天然兴安落叶松的胸径与冠幅数据。通过分析胸径与冠幅之间的关系，选取了3个备选模型，经过拟合与检验，得出幂函数为最优基础模型。然后将最优基础模型与哑变量结合起来，将胸径分为0～20 cm、20～40 cm、>40 cm3个径级，利用哑变量构建了大兴安岭地区天然落叶松冠幅的通用预测模型。采用SAS9.3软件PROC Model模块进行参数的求解，得出哑变量最优模型：CW=(0.353 3G1+0.225 5G2+1.537 6G3)DBH0.587 5G1+0.738 5G2+0.190 4G3。利用加权法消除冠幅预测值的残差，得到比较均匀的残差图。由哑变量参数的估计结果可知，不同径阶的冠幅模型存在显著的不同，因此建议在今后的研究中将林分按照径阶进行分组建模，可以在一定程度上提高模型的拟合效果和预测精度。

虽然胸径生长与冠幅大小呈正相关关系的规律不受立地条件、林分密度、林龄等的影响，但是具体的模型及其参数还是会有或多或少的不同。大兴安岭地区地域辽阔，温度、降雨量等差别比较大，而且各个林场的立地条件也大不相同，每个林场、每个林班的密度也不尽相同，甚至每棵树的林龄以及所在的坡度、坡位、坡向也有一定的不同，而且树高、枝下高、冠长比等因子与冠幅也存在显著相关性。若要考虑以上相关因素，就需要收集与之相关的数据，然而本次研究只有林场及冠幅与胸径的数据，因此如何综合考虑冠幅生长相关的各种因子，构造更准确的冠幅模型，仍需要进一步的研究。

[1]Curtis R O，Reukema D L.Crown Development and Site Estimates in a Douglas-Fir Plantation Spacing Test[J].Forest Science，1970，16(3)：287-301.

[2]Grote R.Estimation of Crown Radii and Crown Projection Area from Stem Size and Tree Position[J].Annals of Forest Science，2003，60(5)：393-402.

[3]田晓筠.林木直径与冠幅的灰色模型及应用[J].科技资讯，2008(25)：86.

[4]韦雪花，王佳，冯仲科.北京市13个常见树种胸径估测研究[J].北京林业大学学报，2013，35(5)：56-63.

[5]唐守正，杜纪山.利用树冠竞争因子确定同龄间伐林分的断面积生长过程[J].林业科学，1999，35(6)：35-41.

[6]符亚健，吕飞舟，朱光玉，等.华北落叶松天然次生林单木冠幅模型构建[J].林业资源管理.2016(5)：65-70.

[7]Gill S J，Biging G S，Murphy A C.Modeling Conifer Tree Crown Radius and Estimating Canopy Cover[J].Forest Ecology and Management，2000，126(3)：405-416.

[8]雷相东，张则路，陈晓光.长白落叶松等几个树种冠幅预测模型的研究[J].北京林业大学学报，2006，28(6)：75-79.

[9]符利勇，孙华.基于混合效应模型的杉木单木冠幅预测模型[J].林业科学，2013，49(8)：65-74.

[10]Krajicek J E，Brinkman K，Gingrich S F.Crown Competition Factor-a Measure of Density[J].Forest Sci，1961，7(1)：35-42.

[11]张金友，姜毛孩，刘德祥.小兴安岭人工樟子松林立木胸径与冠幅直径的相关性[J].林业勘察设计，1997(4)：51.

[12]罗玲，廖超英.榆林沙区樟子松冠幅与胸径的相关关系分析[J].安徽农学通报，2007，13(24)：92-97.

[13]卢昌泰，李吉跃，康强，等.马尾松胸径与根径和冠径的关系研究[J].北京林业大学学报，2008，30(1)：58-63.

[15] Sönmez T.Diameter at Breast Height-crown Diameter Prediction Models for Picea orientalis[J].African Journal of Agricultural Research，2009，4(3)：214-219.

[16]符利勇，唐守正，张会儒，等.东北地区两个主要树种地上生物量通用方程构建[J].生态学报，2015，35(1)：150-157.

[17]李希菲，洪玲霞.用哑变量法求算立地指数曲线族的研究[J].林业科学研究，1997，10(2)：215-219.

[18]李河，麦劲壮，肖敏，等.哑变量在 Logistic 回归模型中的应用[J].循证医学，2008，8(1)：42-45.

[19]高东启，邓华锋，王海宾，等.基于哑变量的蒙古栎林分生长模型[J].东北林业大学学报，2014，42(1)：61-64

[20]曾伟生，唐守正，夏忠胜，等.利用线性混合模型和哑变量模型方法建立贵州省通用性生物量方程[J].林业科学研究，2011，24(3)：285-291.

[21]曾伟生，唐守正.东北落叶松和南方马尾松地下生物量模型研建[J].北京林业大学学报，2011，33(2)：1-6.

[22]杨英，冉啟香，陈新云，等.哑变量在云杉地上生物量模型中的应用研究[J].林业资源管理，2015(6)：71-76.

[23]张甜，朱玉杰，董希斌.抚育间伐对大兴安岭天然用材林冠层结构及光环境特征的影响[J].东北林业大学学报，2016，44(10)：1-7.

Modeling Crown Width for the Opening-grown Trees of NaturalLarixGmeliniPlantation in Daxing’an Mountains1

Zhang Shusen1，Jia Weiwei2*，Wang Yuxia2，Gao Huilin2

(1.Heilongjiang Shangzhi National Forest Farm Management Bureau，Shangzhi 150600；2.School of Forestry，Northeast Forestry University，Harbin 150040)

Based on the investigation data for the naturalLarixgmeliniplantationfrom ten forest bureaus in Daxing’an Mountains，the diameter at the breast height(DBH)and the crown width from four directions(i.e.，east，west，south and north)for all the opening-grown trees in the sample plots were measured.The relationship between theDBHand crown width was analyzed.The linear equation and nonlinear equation were used as the basic models to develop the predicted crown width model for the naturalLarixgmeliniplantation and the optimal model was selected based on the goodness-of-fit and validation results.All the sample trees were classified into three categories(DBH≤20cm，20cm40cm)based on the diameter class.Using the optimal model selected by the goodness-of-fit and validation statistics，the dummy variable approach was employed to develop the general common crown width model for the three classes.The differences of crown width between the three categories were further analyzed.The results showed that both of linear and nonlinear equations were suitable to model the crown width of naturalLarixgmeliniplantation in Daxing’an Mountains.Considering the goodness-of-fit and validation statistics，the nonlinear equation was finally selected as the best model.The general common crown width model for the three categories of the naturalLarixgmeliniplantation wasCW=(0.353 3G1+0.225 5G2+1.537 6G3)DBH(0.587 5G1+0.738 5G2+0.190 4G3).TheparametersofDBH≤20cm，20cm40cmwerenotpassedthettest.

NaturalLarix gmeliniplantation；crownwidthpredictedmodel；dummyvariable；Daxing’anmountains

2017-1-20

横向课题(黑龙江省市县林区森林植被空间分布及多样性研究)；黑龙江省林业厅项目(黑龙江省森林可持续经营试验示范区建设)；大兴安岭地区科技计划项目(大兴安岭林区林分密度调控技术研究及示范)

张树森，学士，高级工程师。研究方向：森林经营。E-mali：zssymp@126.com

张树森，贾炜玮，王玉霞，等.大兴安岭地区天然兴安落叶松疏开木冠幅预测模型[J].森林工程，2017，33(3)：33-38.

U270.1

A

1001-005X(2017)03-0033-06

*通信作者：贾炜玮，博士，副教授。研究方向：林分生长模型。E-mali：Jiaww2002@163.com