区域高等级水准测量中高差改正应用研究

邓芳，李春华

(成都市勘察测绘研究院，四川 成都 610081)

区域高等级水准测量中高差改正应用研究

邓芳*，李春华

(成都市勘察测绘研究院，四川 成都 610081)

结合某地区高等级水准实例，详细分析了水准测量中标尺长度改正、正常水准面不平行改正、重力异常改正及固体潮改正的计算方法，并对以上4项改正数的大小及分布进行了详细的分析，无论是对环闭合差还是高差中误差等精度指标的影响均不显著。因此，为便于水准测量数据处理工作及成果应用，在地形起伏不大的区域高等级水准测量(包括工程测量)实际工作中，可以予以忽略。

水准测量；高差；改正数；精度

1 前 言

《国家一、二等水准测量规范》中外业高差改正包括水准标尺长度及温度改正、正常水准面不平行改正、重力异常改正、固体潮改正和海潮负荷影响改正共6项，并给出了详细的计算公式。本文将结合某区域高等级水准测量实例，就水准标尺长度、正常水准面不平行、重力异常及固体潮4项高差改正的大小及对水准测量中相关精度的影响进行详细讨论，以便于进一步指导高等级水准测量数据处理工作。

2 水准测量各项高差改正的计算方法

高等级水准测量主要包括一、二等水准测量，按照相关规范的要求，各测段高差均须进行标尺长度误差改正、正常水准面不平行改正、重力异常改正和固体潮改正，其计算公式分别如下。

2.1 标尺长度误差改正

标尺长度误差改正计算公式如下：

δ=f×h

(1)

式中：

δ—测段高差改正数，mm；

h—往测或返测高差值，m；

f—标尺改正系数，mm/m。

式(1)表明：标尺长度改正与测段高差及标尺改正数成正比。

2.2 正常水准面不平行改正

在物理大地测量学中，大地水准面是一个最接近平均海水面的重力等位面，它表征了地球的基本几何和物理特性，既是地球形状的数学物理描述，也是陆地高程的起算面和海面地形的基准面。

由于同一水准面上的不同点重力加速度g值不同，则任何两邻近的水准面之间的距离在不同的点上是不相等的，且与作用在这些点上的重力成反比。即水准面之间并不相互平行，这是水准面的一个重要特性，称为水准面不平行性。

正常水准面不平行改正ε的计算如下：

ε=-(γi+1-γi)×Hm/γm

(2)

式中：

γm—两水准点正常重力平均值，10-5m/s2，按式(3)计算；

γi、γi+1—分别为第i与i+1点在椭球面上的正常重力值，10-5m/s2，按式(4)计算；

γm=(γi+γi+1)/2-0.1543Hm

(3)

γ=978032(1+0.0053024sin2φ-0.0000058 sin22φ)/2

(4)

式中：

Hm—两水准点的概略高程平均值，m；

φ—水准点纬度；γ值取至0.01×10-5m/s2。

以上公式表明，正常水准面不平行改正与两点之间的平均绝对高程和纬度有关，当沿子午线方向进行水准测量时，△φ变化最大，ε也最大。在北半球，当水准路线由南向北进行时，纬度增加，△φ为正，ε为负，即两水准面愈加靠近，正高减小。

2.3 重力异常改正

测段重力异常改正λ按照下式计算：

λ=(g-γ)m×h/γm

(5)

式中：(g-γ)m—两水准点的平均空间重力异常值，10-5m/s-2；

水准点布格重力异常值(g-γ)布从国家重力数据库中查取；水准点间的空间重力异常值(g-γ)空计算公式如下：

(g-γ)空=(g-γ)布+0.1119H

(6)

H—水准点的概略高程，m。

可以看出，要得到重力异常改正，需要测量水准点上的重力值。对于非重力水准点，可以由内插布格重力异常求得空间重力异常。

2.4 固体潮改正

海洋潮汐现象是由于月亮和太阳对地球的引力结果，即地球(弹性的流体)也会受到其引力影响而产生不断的变形，称为固体潮现象。对于地球上的某一点来说，它们影响的大小随着它们相对于地球的位置的变化而变化[1]。

一测段高差的固体潮改正数v由下式计算：

v=0.68×[θmcos(Am-A)+θscos(As-A)]×s

(7)

式中：θm、θs—分别为月球、太阳引起的地倾斜；

Am、As—分别为测段平均位置至月球、太阳方向的方位角；

A—观测路线方向方位角；

s—测段长度。

θm、θs由式(8)、式(9)计算：

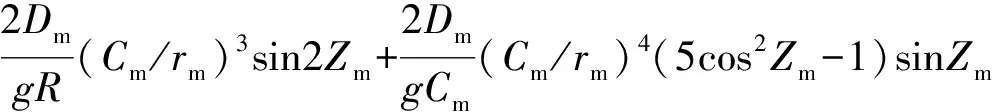
(8)

(9)

式中：Dm、Ds—分别为月球、太阳的杜德逊常数；

R—地球平均曲率半径；g—地球平均重力加速度；

Cm、rm—分别为地心至月球的平均距离和瞬时距离；

Cs、rs—分别为地心至太阳的平均距离和瞬时距离。

Am、As与Zm、Zs由式(10)、式(11)与式(12)、式(13)计算：

cosAm=(sinδmcosφ-sinφcosδmcostm)/sinZm

(10)

cosAs=(sinδscosφ-sinφcosδscosts)/sinZs

(11)

cosZm=(sinφsinδm+cosφcosδmcostm)

(12)

cosZs=(sinφsinδs+cosφcosδscosts)

(13)

式中：φ—测段平均位置的纬度；

δm、δs—分别为月球、太阳的赤纬；

tm、ts—分别为月球、太阳的时角。

δm、δs与tm、ts由式(14)、式(15)与式(16)、式(17)计算：

sinδm=sinεsinλmcosβm+cosεsinβm

(14)

cosδmcostm=cosλmcosβmcosτ+sinτ(cosεsinλmcosβm-sinεsinβm)

(15)

sinδs=sinεsinλs

(16)

cosδscosts=cosλscosτ+sinτcosεsinλs

(17)

式中：ε—黄赤交角；

βm—月球真黄纬；

λm、λs—分别为月球、太阳的真黄经；

τ—观测的地方恒星时。

τ由式(18)计算：

τ=τ0+(TB-8)+(TB-8)/365.2422

(18)

式中：τ0—世界时零点的恒星时；TB—观测时刻时北京时

从式(7)～式(18)看出，只要知道水准测量各测段的观测时间(指北京时间)，即可计算出固体潮改正数[2]。

根据Mel2chior的研究[3]，固体潮引起的地球形状的最大变化可达 ±40 cm，而且具有周期，周期大约为 12 h。在一个周期内，地表面的高度变化一般也在±10 um以内。

3 实例分析

以某地区城市二等水准测量为例，该地区位于北纬43°15′～43°58′之间，测区平均高程约为 220 m，其中水准点高程介于170 m～400 m之间，水准点间高差集中分布在(-20，20)m之间，最大高差约为 70 m，其分布分别如图1所示。

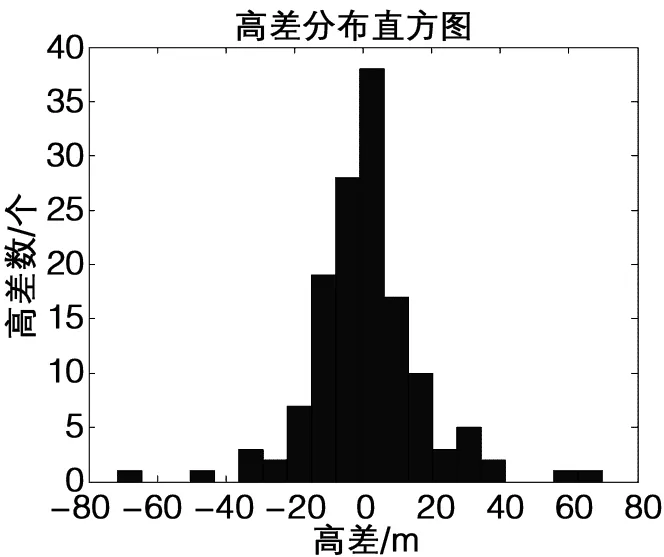
图1 高差分布直方图

尺长改正数介于[-0.39，0.50]mm之间，集中分布于(-0.1，0.1)mm之间，平均改正数为0，其分布如图2所示。

水准面不平行改正数介于[-0.80，1.06]mm之间，集中分布于(-0.5，0.5)mm之间平均改正数为 0.05 mm，最大改正数的平均高程明显高于该地去的平均高程，其分布如图3所示。

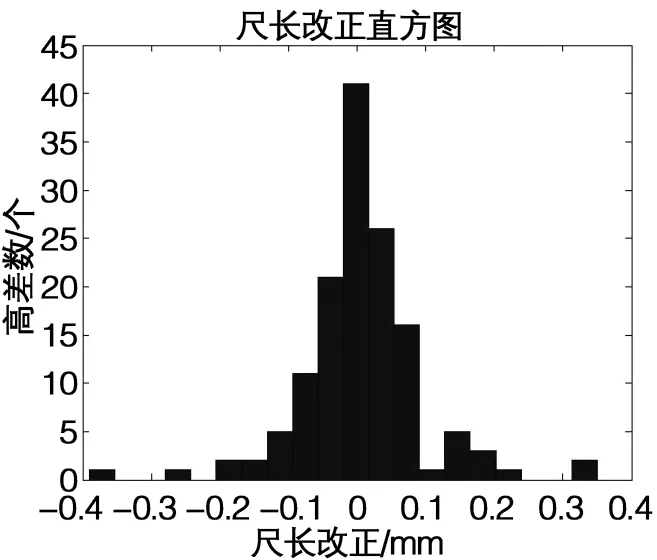
图2 尺长改正分布图

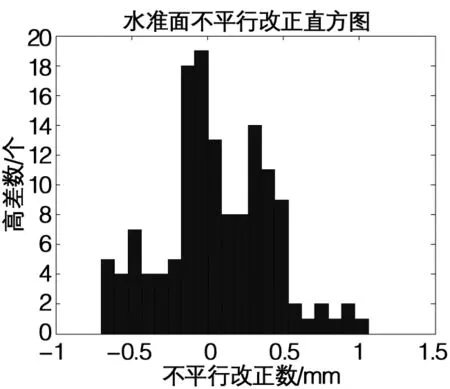
图3 水准面不平行改正分布图

重力异常改正数介于[-1.96，3.26]mm之间，平均改正数为 0.02 mm，其中绝大部分改正数介于(-0.5，0.5)mm之间，最大高差改正数的高差约为 70 m，其高差均其分布如图4所示。

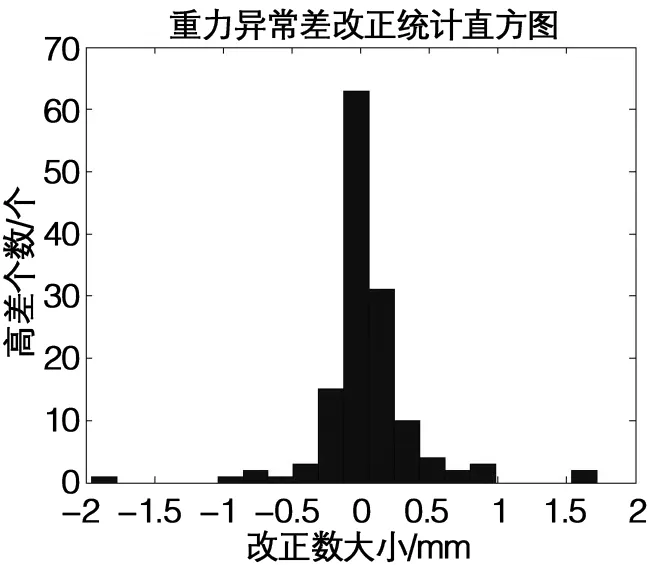
图4 重力异常改正分布图

固体潮改正数介于[-0.46，0.26]mm之间，集中分布于(-0.2，0.2)mm之间，平均改正数为 -0.01 mm，其分布如图5所示。

以上4项高差总改正数介于[-1.61，2.83]mm之间，平均改正数为 0.1 mm，其中绝大部分改正数介于(-1.0，1.0)mm之间，其分布如图6所示。各个闭合环统计见表1，其中闭合差1与闭合差2分别为由原始观测高差和加上4项高差改正数后的高差计算结果。

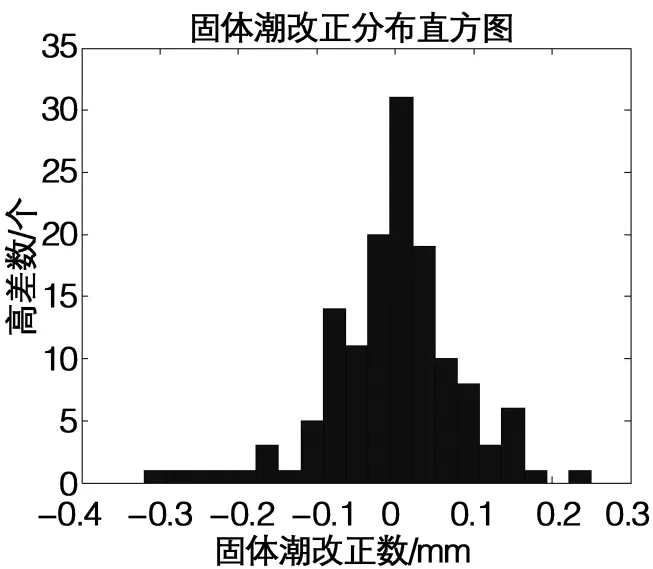
图5 固体潮高差改正分布图

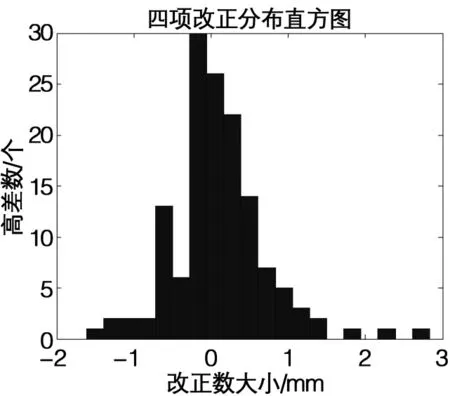
图6 四项高差总改正数分布图

无论是闭合差1与闭合差2，均大大优于二等水准限差的要求，加上高差改正数后对闭合差的影响最大约为 1 mm。且通过环闭合差计算的每千米高程测量的高差中误差分别为±0.67 mm与±0.62 mm，通过[PVV]计算的单位权中误差分别为±0.64 mm与±0.60 mm。

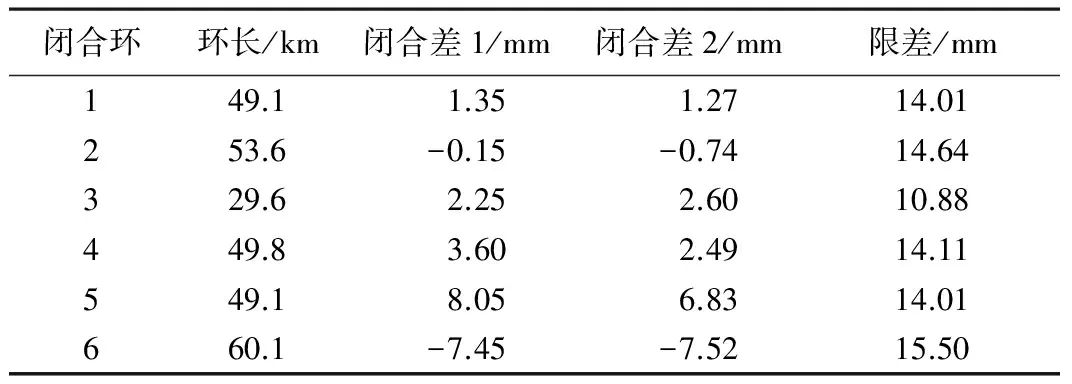
环闭合差统计表 表1

表1的数据分析表明，就单位权中误差而言，虽然加上各项改正后略有改善但不显著，对环闭合差的影响更小。

4 结论与建议

在地形起伏不大的地区(如城市或工程建设)，二等及以上的高等级水准测量中的水准标尺长度改正、正常水准面不平行改正、重力异常改正、固体潮改正对水准测量精度(如环闭合差、高差中误差)的影响甚小，为便于实际工作及应用，可不必进行高差改正，尤其是固体潮改正及重力异常改正(计算较为烦琐)。

[1] 何晓业. 重力异常对静力水准系统测量精度的影响[J]. 大地测量与地球动力学，2009，26(1)：124～127；

[2] 薄万举，陈聚忠，地震水准测量成果中几项改正的讨论[J]. 大地测量与地球动力学，2011，31(4)：34～37；

[3] DavidMartin. Some reflections on the validation and analysis of HLS data[A]. Proceedings of the 8 th International Workshop on Accelerator Alignment[C]. Oct. 7-4，2004，CERN，Geneva，Switzerland.

[4] GB/T 12897-2006. 国家一、二水准测量规范[S].

[5] 梁振英，董鸿闻，姬恒炼，精密水准测量的理论与实践[M]. 北京：测绘出版社，2004.

Application of Corrections for Elevation Difference in Regional High Accuracy Leveling

Deng Fang，Li Chunhua

(Chengdu City Institute of Surveying and Investigation，Chengdu 610081，China)

Combined with example of high accuracy leveling somewhere，this article analyzes methods of computing few corrections and their distribution in leveling in detail，including leveling rod length correction，quasi-geoid slope correction，gravity anomaly correction，and solid tide correction.Results show that all these corrections have little impact on precision index like closing error，mean squre error of height and so on. So they nearly can be negligible in high accuracy leveling around area with flat topography.

leveling surveying；elevation difference；correction；precision

1672-8262(2017)02-127-04

P224.1

A

2016—12—08

邓芳(1978—)，女，硕士，高级工程师，主要从事RS、GIS、GPS技术及工程测量等等方面的应用研究。