带有齿隙的空间机械臂动力学仿真与试验设计
李思远, 陈子坤, 梁 曦, 石亦琨, 魏 承, 赵 阳
(1. 哈尔滨工业大学 航天学院, 黑龙江 哈尔滨 150001; 2. 北京航空航天大学 航空科学与工程学院, 北京 100191;3. 首都航天机械公司, 北京 100076)
带有齿隙的空间机械臂动力学仿真与试验设计
李思远1, 陈子坤2, 梁 曦1, 石亦琨3, 魏 承1, 赵 阳1
(1. 哈尔滨工业大学 航天学院, 黑龙江 哈尔滨 150001; 2. 北京航空航天大学 航空科学与工程学院, 北京 100191;3. 首都航天机械公司, 北京 100076)
本文以带有齿隙的空间机械臂为研究对象, 通过气悬浮的方式实现微重力的模拟, 用改变一对标准渐开线支持圆柱齿轮中心距的方式, 实现关节齿隙的连续可调, 设计了试验验证机构的三维模型, 并基于ADAMS搭建其动力学模型对多齿隙机械臂的动力学模型进行仿真分析. 对模型进行加工装配后, 设计控制系统、 测量系统和供气辅助系统, 并设计验证试验, 使其能够实现对于不同齿隙情况, 反映微重力环境下齿隙对机械臂系统动力学特性的影响, 为延长空间机械臂的使用寿命提供理论指导.
微重力; 标准渐开线直齿圆柱齿轮; 动力学模型
随着航天技术的高速发展, 人们逐渐提高了对航天器的需求, 航天器能够完成的任务越来越多, 其尺寸越来越大, 复杂程度越来越高, 航天器的发展将朝着长寿命、 高可靠性、 高精度、 大型化、 复杂化的方向发展[1]. 航天器的功能大多需要依靠安装在其上的机械机构来完成, 但是航天机构工作的空间环境十分恶劣, 微重力、 强辐射、 高低温等空间环境对机构的特性退化有很大的影响, 随着使用时间的增加, 其运动部件之间的磨损则不可忽略, 而齿隙的增加直接影响着机构的定位精度, 当齿隙逐渐增大时, 由于机构的动力学特性的恶化, 会导致机构失效[2,3]. 本文基于以上亟待解决的问题展开研究, 落脚点在于机械臂中多齿隙对其动力学响应的影响, 通过搭建微重力条件[4,5]下三关节多齿隙的空间机械臂的试验验证系统, 对比分析试验与仿真数据, 最终得到齿隙对机械臂动力学的影响规律, 进而得到齿隙对航天机构可靠性的影响.
1 带有齿隙的机械臂试验机构的理论分析
1.1 试验机构的受力分析
对于基本规律研究, 为了该规律的通用性, 选择每个关节的传动形式为单对渐开线直齿圆柱齿轮传动, 即相互啮合的两个齿轮, 一个与关节基准固定并提供关节的输入, 另一个与该关节的输出臂杆固定, 提供关节的输出. 由于根部关节与惯性坐标系固定, 若实现机构的微重力环境, 主要需要对从动轮及臂杆等运动部件进行重力补偿作用, 所以对从动轮、 臂杆和负载进行受力分析. 将负载与臂杆看成一个物体, 讨论其与从动轮的受力关系, 如图 1 所示. 由于关节输出部位属于对称结构, 所以只分析其在竖直平面内的受力情况.

图 1 机械臂受力分析示意图Fig.1 Diagram of schematic arm stress analysis
当没有重力补偿项时, 受力情况为
根据微重力环境模拟的目的可知, 只有当F和M同时为0时, 臂杆与负载的重力才能完全由补偿项进行补偿, 即臂杆与负载处于微重力状态, 从动轮只对臂杆提供使其运动的驱动力, 而不受静平衡力的作用.
1.2 带有齿隙的双齿轮啮合模型
影响齿隙的主要因素有两方面: 一是轴承处的齿隙反应在齿轮沿其径向的晃动量, 二是齿轮啮合时沿节圆和啮合线方向的晃动量. 就齿隙而言, 可将其分成3类: 径向齿隙、 轴向齿隙和法向齿隙. 而对于齿轮来说, 啮合过程中重要的物理量是齿轮的基圆、 节圆和啮合线, 对于齿廓来说, 啮合过程中最重要的参考点是啮合点、 主从动轮齿廓与啮合线的交点、 主从动轮齿廓与各自节圆的交点, 共5个点即可描述齿侧法向齿隙和轴向齿隙. 本文采用调整中心距的方法来调整齿侧间隙, 因此需要研究齿轮中心距变化时, 齿轮啮合状态的数学模型中与中心距直接相关的物理量, 从而得到实际啮合情况与标准啮合情况, 如图 2 所示.

(2)
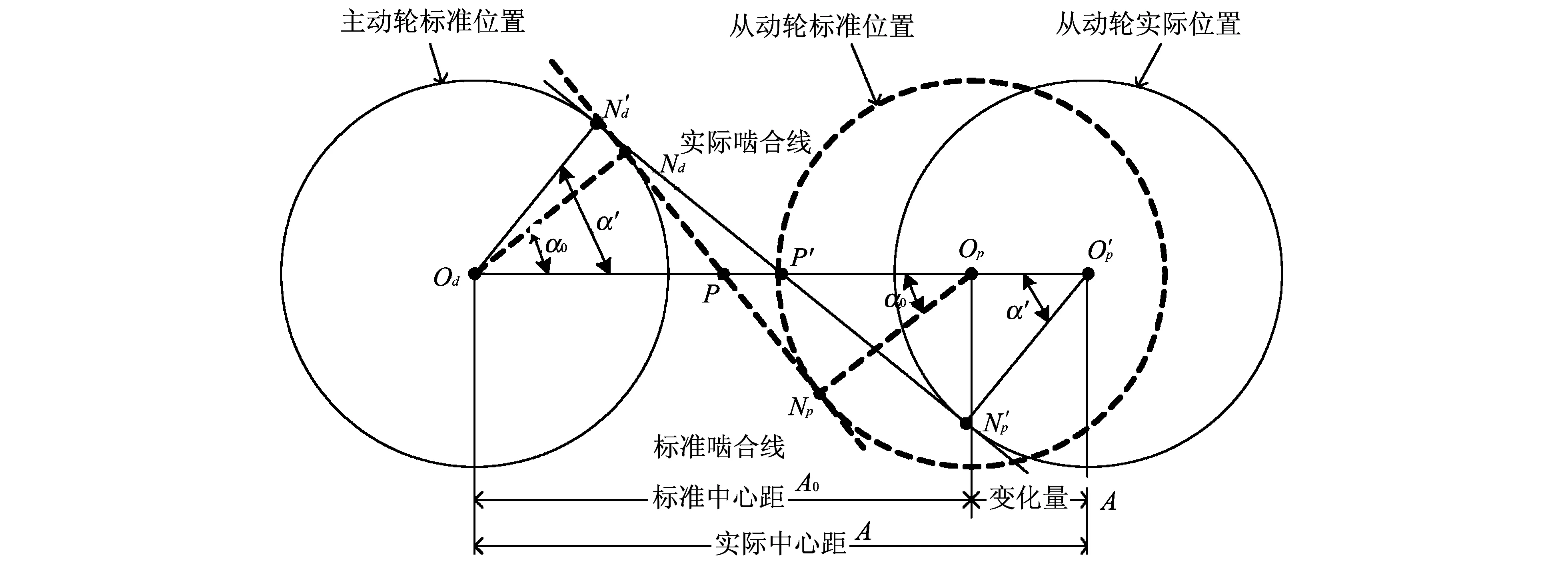
图 2 实际啮合情况与标准啮合情况的对比图Fig.2 Comparison chart of actual meshing and engagement with the standard case
图 3 为单对标准渐开线直齿圆柱齿轮啮合部分的数学模型, 选取两齿轮轮齿在工作面发生接触且啮合点恰好位于齿轮中心连线时的特殊状态, 以便分析齿侧间隙.
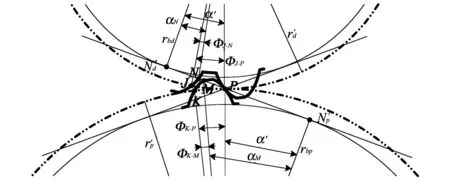
图 3 单对标准渐开线直齿圆柱齿轮啮合模型Fig.3 Single standard involute spur gear meshing model

Cn=PN-PM=MN.
(3)
齿轮的轴向齿侧间隙可表示为
Cc=PJ-PK.
(4)
数学模型中各个角度的定义为:α′为P点在主动轮和从动轮中的压力角, 即齿轮节圆上的压力角, 两齿轮在该位置的压力角相等;αN为N点在主动轮中的压力角,αM为M点在从动轮中的压力角;ΦJ-P为主动轮齿槽宽度角,ΦK-P为从动轮的齿厚宽度角;ΦJ-N为主动轮齿廓上J点与N点展成角之差,ΦK-M为从动轮齿廓上K点与M点展成角的差. 由几何关系可推得齿轮轮齿齿侧法向齿隙和轴向齿隙之间的关系, 即瞬时齿侧法向齿隙等于该时刻齿侧轴向齿隙与实际节圆压力角余弦值的乘积.
1.3 带有齿隙的齿轮碰撞力模型
齿轮在接触过程中, 力的方向始终沿着啮合线的方向, 且垂直于齿廓在接触点的切线, 所以齿轮碰撞力Fn可以表示为法向齿隙Cn和法向嵌入量δn的函数, 即
再根据Hertz接触碰撞模型与Liu[6,7]提出的改进的非线性弹性碰撞力模型, 可得带有齿隙齿轮啮合接触碰撞力为
由式(7)可以看出, 齿轮间沿轮齿齿廓的法向接触碰撞力Fn与齿轮的标准中心距A0、 齿轮的标准压力角α0、 齿轮的实际中心距A、 接触面的综合弹性属性E、 轮齿的恢复系数e、 轮齿临界接触状态时接触点的相对速度v0和齿轮实际节圆传动误差gc有关. 其中,A0,α0,A,E,e在确定相互啮合的两齿轮过程中即可确定,v0,gc需根据齿轮的实际啮合状态加以确定. 由此可以看出,Fn还是时间t的函数, 而且还与每次碰撞的初始状态有关.
2 带有齿隙的机械臂系统设计
图 4 为带有齿隙机械臂试验系统示意图, 从中可以看出各个分系统的组成.

图 4 带有齿隙机械臂试验系统示意图Fig.4 The whole system schematic of manipulator with gap
试验验证机构即为平放在铁架台和气浮台上的带有齿隙三关节机械臂模型, 主要由根部关节、 中间关节、 末端关节和末端负载串联组成.
控制系统采用型号为GYS401DC2-T2C的富士伺服电机对机械臂进行控制, 并由型号为RYC401D3-VVT2的电机驱动器对伺服电机进行控制, 以得到期望的关节输入量, 电机的电控部分由PXIe-6624采集卡完成, 在上位PC机中通过Labview软件编程, 将指令下达到NI处理器中, 即可按照程序实现对电机运动状态的控制.
测量系统用来采集加速度信号与力矩信号. 臂杆末端的三轴加速度计采用YE6267动态采集测试系统, 通过Labview软件编程实现上位机与NI设备的控制, 由16个独立的信号调理通道、 经16个16 b的A/D采集后由USB接口传入PC机, 通道带宽为100 kHz, 采样频率100KSPS/CH, 分档可选. 而力矩传感器的信号先通过相应的放大器将传感器产生的信号放大, 再将信号传入到PXIe-6363板卡中的相应数据采集端口, 进而通过NI设备将实时测量的信号返回到主控电脑PC中[8,9].
供气辅助系统的主要组件由空气压缩机、 高压气管、 高压气管的相关固定部件和连接组件组成, 高压气体由空气压缩机压缩得到, 然后通过高压气管到达每个气足处, 从而实现机械臂的微重力环境.
3 带有齿隙机械的臂系统动力学仿真
利用Solid Works搭建单关节、 双关节和三关节机械臂的三维模型, 并将其导入ADAMS, 在相应部位加入约束、 驱动、 力和相关测量, 再利用ADAMS中的动力学模型实现相关量的输入与输出. 根据试验验证系统的详细设计以及最后的装配图, 导入ADAMS机械臂的三维模型, 以单关节为例, 如图 5 所示.

图 5 单关节机械臂的三维模型Fig.5 Single joint manipulator 3D model
对机械臂的动力学特性的仿真分析, 主要关注每个关节处的输出轴转速、 输出轴传动力矩, 并研究不同齿隙对这些量的影响规律. 基于动力学问题的基本研究可知, 当机械臂中存在单一齿隙和多个齿隙时, 其动力学响应的规律是不同的[10], 因此需分别研究单关节、 双关节和三关节的动力学模型, 本文为与试验进行对比, 以单关节为例, 臂杆的摆动设定为45°, 主动轮中心距的取值为0.2 mm, 0.6 mm, 主动轮转动周期的取值为4 s, 8 s, 负载质量的取值为20 kg, 从而得到以下的动力学仿真, 如图 6~图 9 所示.
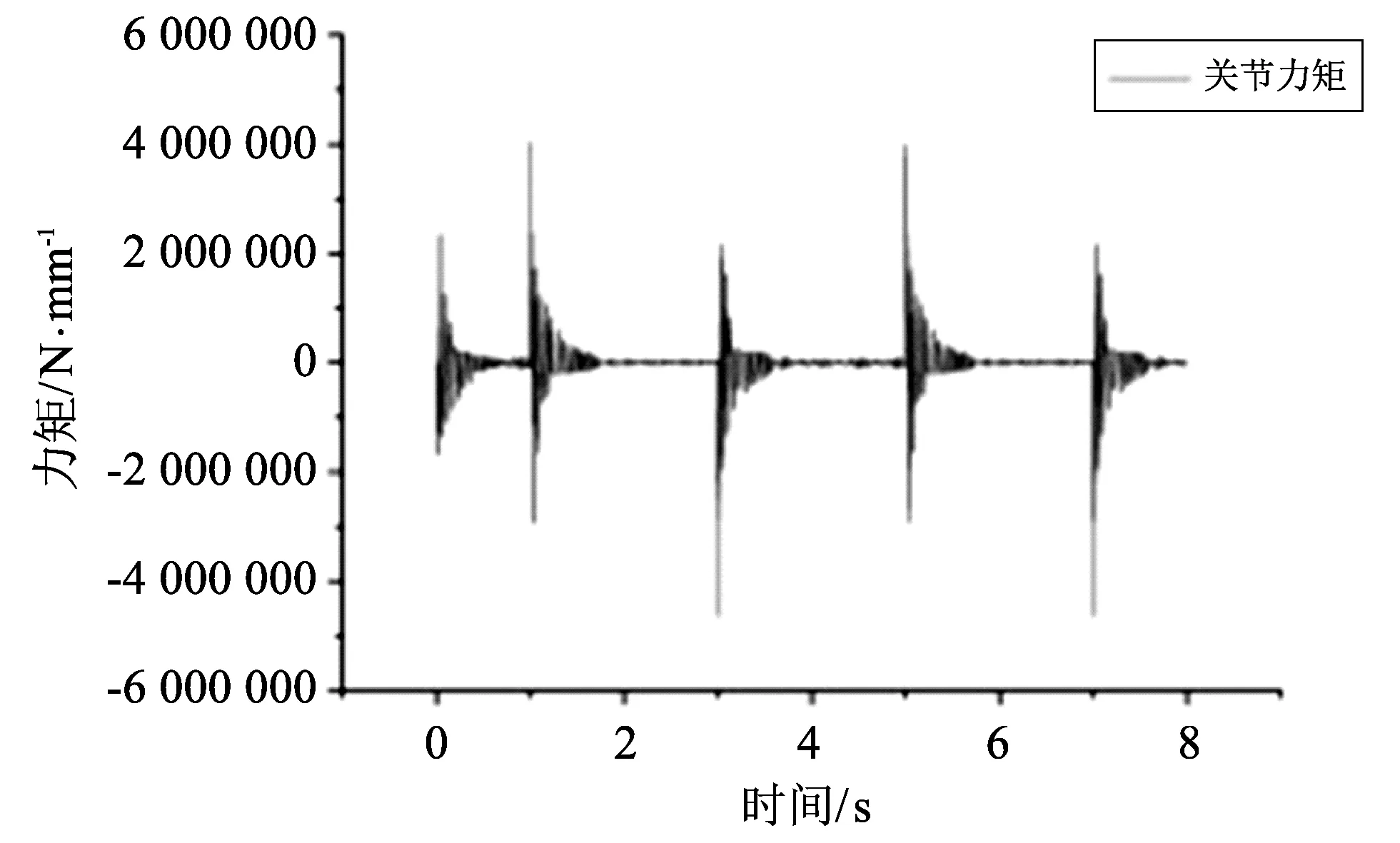
图 6 中心距0.2 mm, 转动周期4 s传动力矩Fig.6 The drive torque for 0.2 mm center distance and 4 s rotation period
图 7 中心距0.6 mm, 转动周期4 s传动力矩Fig.7 The drive torque for 0.6mm center distance and 4 s rotation period

图 8 中心距0.2 mm, 转动周期8 s传动力矩Fig.8 The drive torque for 0.2 mm center distance and 8 s rotation period
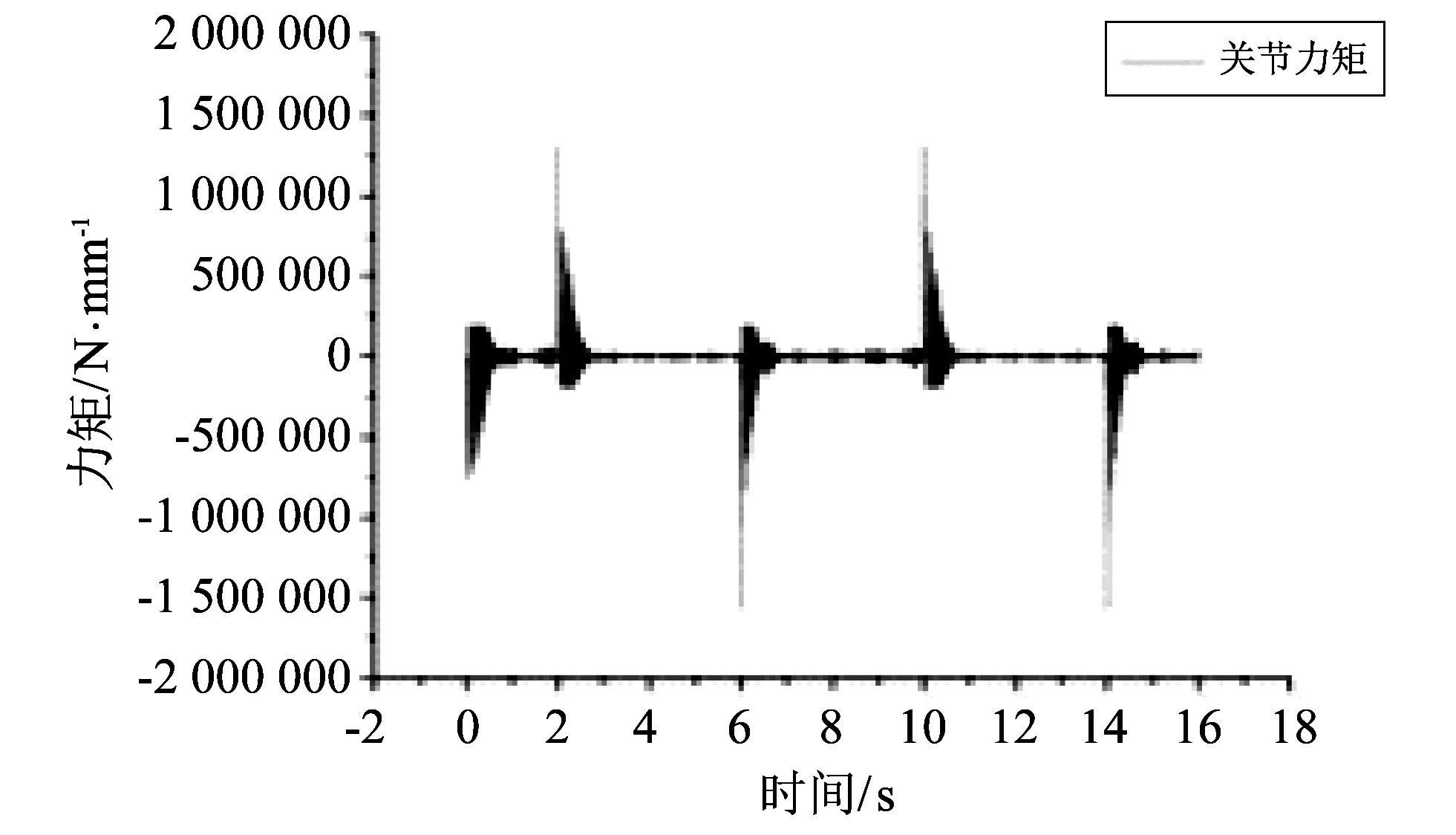
图 9 中心距0.6 mm, 转动周期8 s传动力矩Fig.9 The drive torque for 0.6 mm center distance and 8 s rotation period
当齿隙变大时, 关节传动力矩的稳定时间变长, 这是由于齿轮是靠轮齿工作面与非工作面的碰撞作用实现稳定的传动比, 当齿隙增大时这种碰撞作用发生的频率降低, 所以齿轮机构达到稳定传动比的时间变长.
4 带有齿隙机械的臂系统实验

图 10 试验验证机构实物图Fig.10 Actual picture of the experimental verification mechanism
由于每个关节的关节形式相同, 所以只对单关节机械臂动力学试验系统进行测试, 试验实物如图 10 所示, 将基座部分固定在长方形铁架台的中间部分, 使得臂杆在尽可能大的范围内运动, 机械臂部分完全在气浮平台上运动. 适当调整气足的位置, 使气足在通气的状态下完全承受关节的重力. 主动轮在控制系统下做往复摆动运动, 摆动的幅角为45°, 动轮转动周期的取值为4 s, 8 s, 负载质量的取值为20 kg, 由于试验中对齿轮中心距变化量的测量是用螺旋测位仪测量的, 所以中心距改变量的值保留到小数点后3位, 分别为0.211 mm, 0.606 mm.
转动周期为4 s, 8 s, 中心距为0.211 mm, 0.606 mm, 0.100 mm, 所对应的从动轮和臂杆之间的输出传动力矩值如图 11~图 13 所示.
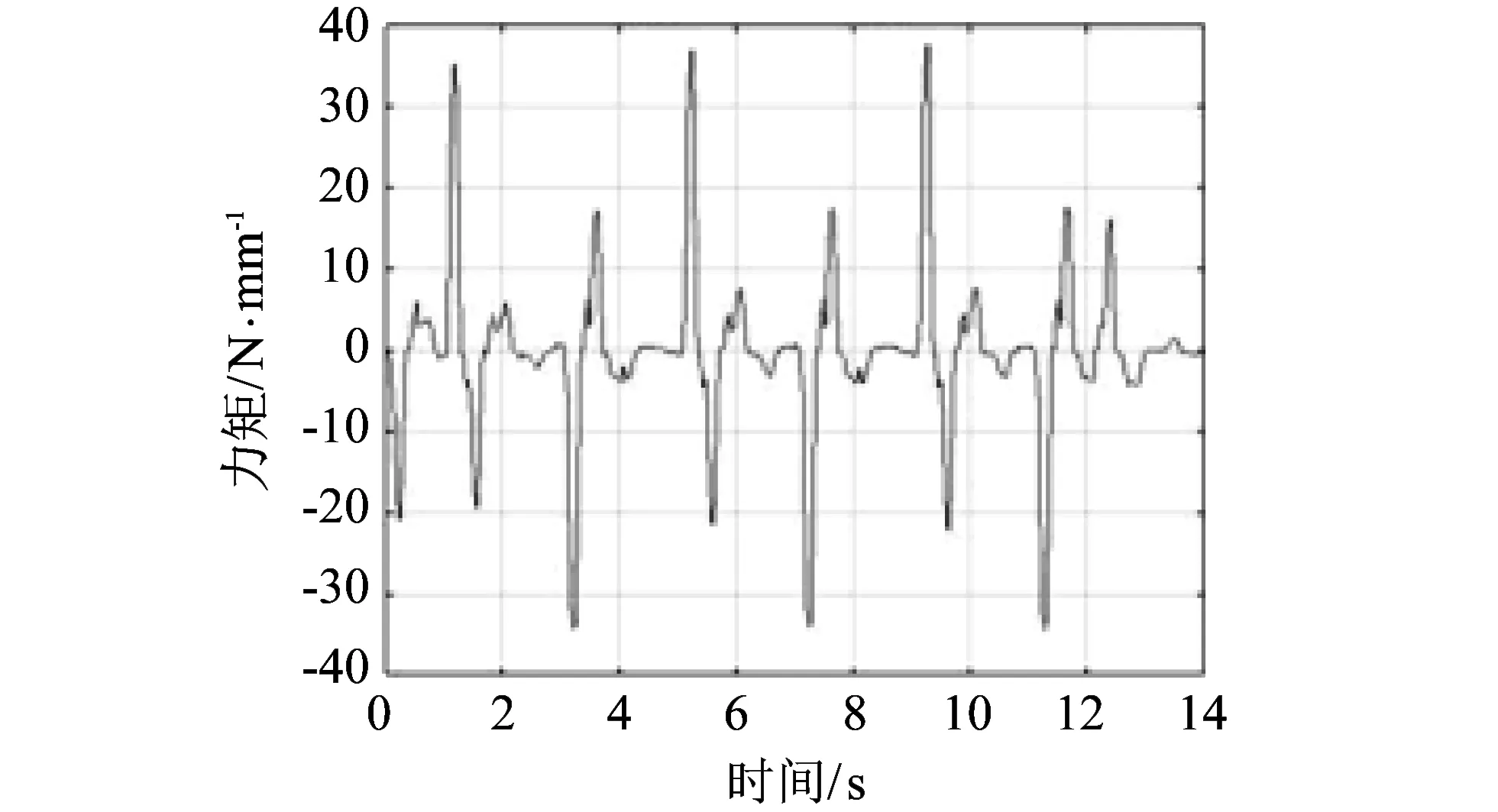
图 11 转动周期4 s, 中心距0.211 mm传动力矩Fig.11 The drive torque for 0.211 mm center distance and 4 s rotation period
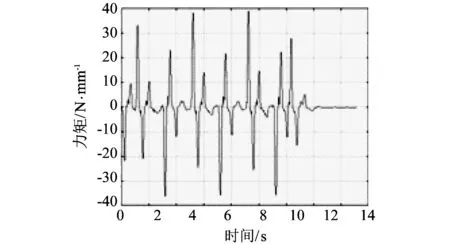
图 12 转动周期4 s, 中心距0.606 mm传动力矩Fig.12 The drive torque for 0.606 mm center distance and 4 s rotation period

图 13 转动周期8 s, 中心距0.211 mm传动力矩Fig.13 The drive torque for 0.211 mm center distance and 8 s rotation period
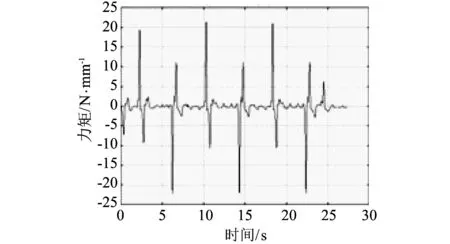
图 14 转动周期8 s, 中心距0.606 mm传动力矩Fig.14 The drive torque for 0.606 mm center distance and 8 s rotation period
在相同转速不同齿隙的情况下, 当齿隙值增大时, 力矩的峰值逐渐变大, 但齿隙增大到某一特定值后, 力矩峰值不会发生明显变化, 而且不同转速时该特定值也不相同. 而当转速相同时, 齿隙越大, 齿轮碰撞的次数越少, 且两次碰撞的间隔越长, 则机构间摩擦的作用时间延长, 能够减少从动轮达到期望转速的时间.
5 结 论
本文以多齿隙机械臂为研究对象, 研究了齿侧间隙的精确数学模型, 以此设计搭建了连续可变齿隙的机械臂试验验证机构, 并对其进行动力学仿真和验证试验, 最后总结出关节齿隙与机械臂动力学特性之间的响应规律, 可以为空间机械臂的在轨控制提供理论支持, 从而提高航天机构的使用寿命.
[1] 张文辉, 叶晓平, 季晓明. 国内外空间机器人技术发展综述[J]. 飞行力学, 2013, 31(3): 198-202. Zhang Wenhui, Ye Xiaoping, Ji xiaoming. Development summarizing of space robot technology national and outside[J]. Flight Dynamics, 2013, 31(3): 198-202. (in Chinese)
[2] 张凯锋, 周晖, 温庆平. 空间站机械臂研究[J]. 空间科学学报, 2010, 30(6): 612-619. Zhang Kaifeng, Zhou Hui, Wen Qingping. Review of the development of robotic manipulator for international space station[J]. Chinese Journal of Space Science, 2010, 30(6): 612-619. (in Chinese)
[3] 李大明, 饶炜, 胡成威. 空间站机械臂关键技术研究[J]. 载人航天, 2014, 20(3): 238-242. Li Daming, Rao Wei, Hu Chengwei. Key technology review of the research no the space station manipulator[J]. Manned Spaceflight. 2014, 20(3): 238-242. (in Chinese)
[4] 曲春成. 空间机械臂地面微重力模拟系统研究与实现[D]. 哈尔滨: 哈尔滨工业大学, 2014.
[5] Watanabe Y, Araki K, Nakamura Y. Microgravity experiments for a visual feedback control of a space robot capturing a target[C]. Intelligent Robots and Systems, 1998. Proceedings, 1998 IEEE/RSJ International Conference on, 1998: 1993-1998.
[6] Liu C S, Zhang K, Yang L. Normal force-displacement relationship of spherical joints with clearances[J]. Journal of Computational and Nonlinear Dynamics, 2006, 1(2): 160-167.
[7] 秦志英, 陆启韶. 基于恢复系数的碰撞过程模型分析[J]. 动力学与控制学报, 2006, 4(4): 294-298. Qin Zhiying, Lu Qishao. Analysis of impact process model based on restitution coefficient[J]. Journal of Dynamics and Control, 2006, 4(4): 294-298. (in Chinese)
[8] 孟武胜, 朱剑波, 黄鸿. 基于LabVIEW数据采集系统的设计[J]. 电子测量技术, 2008, 31(11): 63-65. Meng Wusheng, Zhu Jianbo, Huang Hong. Data acquisition system based on LabVIEW[J]. Electronic Measurement Technology, 2008, 31(11): 63-65. (in Chinese)
[9] 林爽, 杨风. 基于LabVIEW的多通道数据采集系统的研究[J]. 陕西电子技术, 2009(3): 18-20. Lin Shuang, Yang Feng. The research of multichannel DAQ system based on LabVIEW[J]. Shanxi Electronic Technology, 2009(3): 18-20. (in Chinese)
[10] 卢剑伟, 陈昊, 孙晓明. 考虑减速机构间隙的机械臂动力学建模分析[J]. 机械工程学报, 2013, 49(15): 134-139. Lu Jianwei, Chen Hao, Sun Xiaoming. Dynamic modeling and analysis of robot arm with consideration of clearance in gear reducer[J]. Journal of Mechanical Engineering, 2013, 49(15): 134-139. (in Chinese)
Dynamical Simulation and Experimental Design of Space Manipulator with Backlashes
LI Siyuan1, CHEN Zikun2, LIANG Xi1, SHI Yikun3, WEI Cheng1, ZHAO Yang1
(1. School of Astronautics Aerospace Engineering, Harbin Institute of Technology, Harbin150001, China;2. School of Aeronautic Science and Engineering, BeiHang University Beijing 100191, China;3. Captial Spaceflight Machinery Company, Beijing 100076, China)
Taking space manipulator with backlashes for research object, theair-floatation equipment is used to achieve the microgravity environment, and a pair of standard involute center distances of the cylindrical gear is changed to continuously adjust the backlashes of joint. Three-dimensional model of the mechanism of experimental verification are designedbased on ADAMS. After assembling the model, design the control system, measuring system and air-floatation auxiliary system, and design the verification test to make it can reflect the dynamical impact of space manipulator system For different backlashes in the microgravity environment, in order to provide theoretical guidance to extend the life of the space manipulator.
microgravity; standard involute spur gear; dynamical model
1671-7449(2017)01-0017-07
2016-11-18
国防重点学科实验室开放基金资助项目
李思远(1991-), 男, 硕士, 主要从事飞行器系统动力学与传真研究.
V423.9
A
10.3969/j.issn.1671-7449.2017.01.003

