任意密度分布复杂地质体重力异常快速三维正演方法

陈轻蕊， 陈龙伟， 戴世坤， 张钱江， 欧阳芳

(1.中南大学 地球科学与信息物理学院，长沙 410083; 2.桂林理工大学 地球科学学院，桂林 541006)

任意密度分布复杂地质体重力异常快速三维正演方法

陈轻蕊1， 陈龙伟2， 戴世坤1， 张钱江1， 欧阳芳1

(1.中南大学 地球科学与信息物理学院，长沙 410083; 2.桂林理工大学 地球科学学院，桂林 541006)

解决任意密度分布复杂地质体重力异常三维正演快速、高精度计算问题，是实现重力三维反演、人机交互解释建模的关键。针对该问题，从积分方程出发，提出一种波数域重力异常三维正演方法，其关键环节包括三个方面：①将研究区域剖分成许多规则小棱柱体，每个小棱柱体密度值可以任意给定，以此刻画任意密度分布和起伏地形条件下的复杂地质体；②给出一种新的高精度均匀棱柱体重力异常二维波数域的计算公式，用于计算组合棱柱体模型的重力异常；③采用Gauss-FFT法将重力异常从波数域转换到空间域，保证计算效率的同时，有效克服了传统FFT法引起的边界效应问题。模型算例检验结果表明，该算法计算速度快、精度高，对于剖分为百万个棱柱体的模型，耗时只需几秒。

重力异常； 三维正演； Gauss-FFT； 积分方程

0 引言

随着观测数据的急剧增加，重力反演已由近似的二维反演发展到符合实际情况的三维反演。正演是反演的基础，任意密度分布复杂地质体重力异常快速、高精度三维正演是实现重力三维反演、人机交互解释建模的关键。解决重力异常三维正演问题，既可以从偏微分方程边值问题入手，也可以从三维积分入手，两者理论上是等价的，但由两种思路得到的数值方法在计算效率和计算精度两方面的表现是不同的。

从偏微分方程的边值问题角度来求解三维正演问题，主要采用的数值方法包括有:①限单元法;②有限差分法;③有限体元法。微分方法的关键环节主要包括:①边值条件给定;②稀疏矩阵方程求解。CAI Y[1]提出了一种新的边界条件，提高了数值结果精度，并通过采用一种加权函数策略来直接求解节点上的重力值，避免了传统有限单元法中先计算高斯点重力值再通过插值计算节点重力值，计算效率得到提高；C G Farquharson[2]从重力场高斯定理出发，采用有限差分法求解泊松方程，由于满足其次边界条件，使用时计算区域边界需要远于实际异常区域边界，提高计算精度的同时降低了计算效率；May D A[3]对比研究了直接累加法、有限元法和快速多偶极子法；Jahandari H[4]采用了非结构化网格有限元法求解重力偏微分方程；Guzman S[5]采用有限体元法直接对重力场进行求解。偏微分方法的一个优势是能够一次计算所有节点上的场值，生成的系数矩阵为稀疏矩阵，存储要求低，但目前这类方法的计算效率还是较低。

用积分方程求解重力三维正演问题的研究相对更多一些，大致可分为：①空间域方法；②波数域方法。

空间域法主要是推导规则几何形体的解析解，对复杂结构形态和非均匀密度分布的地质体采用已有解析解的几何体的模型剖分或近似，通过组合求和得到整个复杂形体的场值[6]。利用积分求解析解的优点是可精确地求出空间任意点的场值，缺点在于不同的模型的解析式往往较为复杂，推导过程比较繁琐，对于密度连续变化的模型需要剖分很多段才能算准，当形体复杂、需要计算大量异常数据时，计算量大，速度较慢。

波数域方法将重力积分进行二维或三维傅里叶变换[7]，借助FFT算法实现场的高效计算。由于离散采样等原因，传统FFT存在边界效应问题，导致计算精度低，通常需要进行扩边来减小边界效应，提高计算精度，但这使得计算量增大。Wuly[8]在偏移抽样理论[9]的基础上，提出一种实现傅里叶变换高精度数值计算的Gauss-FFT方法。该方法能有效抑制边界效应，且能避免零波数计算时的奇异问题，十分适合于波数域方法。

笔者从积分方程出发，提出一种波数域三维正演方法。该方法给出了一种新的组合棱柱体模型波数域重力异常表达式，借助Gauss-FFT方法，很好解决了任意密度分布复杂地质体快速、高精度重力异常三维正演问题，为解决大规模重力异常三维反演和人机交互解释提供了有力的方法支持。

1 新方法原理

为了模拟任意密度分布三维复杂地质体，我们采用的策略是将研究区域剖分成很多个规则小棱柱体，每个棱柱体的密度为常值，剖分棱柱体个数越多，模型刻画越精细。这种策略十分适合于重力异常三维反演[10-12]和人机交互解释建模[13-14]。依据重力异常的叠加原理，复杂地质体的重力异常计算问题，可以转化为组合棱柱体的重力异常的计算问题(图1)。

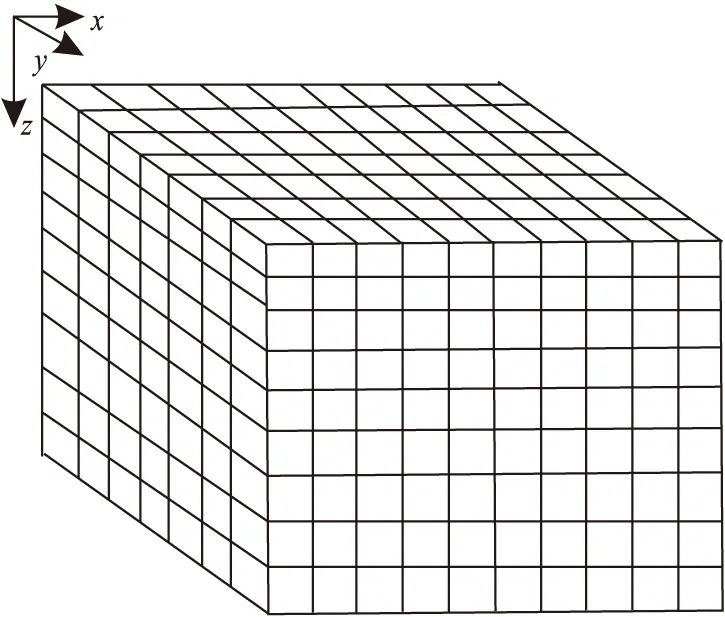
图1 组合棱柱体示意图Fig.1 Illustration of combined prism model

快速、准确计算组合棱柱体产生的重力异常，是我们研究的重点。组合棱柱体的重力异常gz可以表示为:

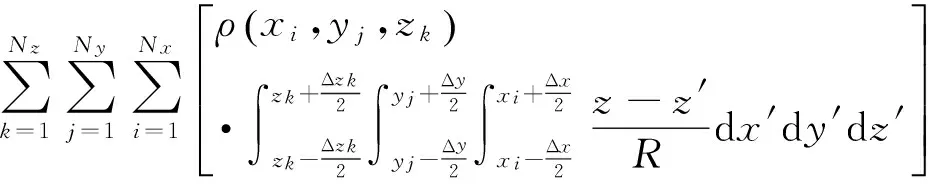
(1)

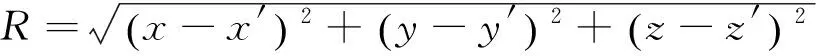
笔者提出的波数域重力异常快速、高精度三维正演方法，关键环节之一是对式(1)两边施加二维傅里叶变换，推导得到一种新的重力异常波数域表达式，将式(1)左右两边进行二维傅里叶变换，可得式(2)。

(2)

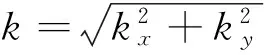
(3)

式(3)在形式上类似于二维离散傅里叶变换，在数值计算实现时，可利用快速傅里叶算法(FFT)实现。

在式(2)的推导过程中，利用了式(4)与式(5)两个中间结论。

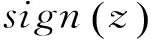
(4)

式中：sign(·)表示符号函数。

(5)

从理论上来说，空间域重力异常可通过二维傅里叶反变换得到。

(6)

2 数值算法

这里给出基于Gauss-FFT法的重力异常数值计算公式。对式(6)离散过程中，需要对空间域坐标和波数域坐标分别进行离散化，我们采用文献[15]中的方法，给出任意采样点情况下离散空间域坐标和离散波数值(以采样点个数为偶数为例，奇数情况离散波数)如下:

xm=x1+(m-1)Δxm=1,2,…,Nx

(7)

yn=y1+(n-1)Δyn=1,2,…,Ny

(8)

kp=p·Δkx

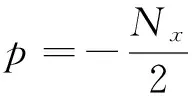
(9)

kq=q·Δky

(10)

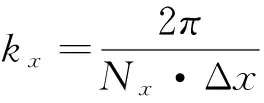
(11)

(12)

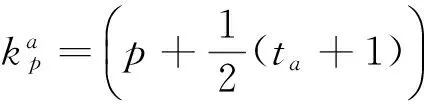
(13)

(14)

式中：ta、tb是区间[-1,1]上高斯点[16]的坐标；Aa、Ab为相应的高斯点加权系数。

根据Gauss-FFT法[8]离散傅里叶变换计算公式，可得波数域重力异常计算式为式(15)。

(15)

式中:

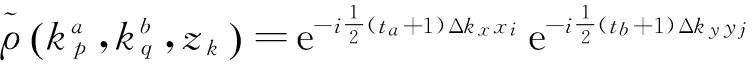
(16)

式中：大括号的部分利用FFT算法实现。

空间域重力异常数值计算表达式为式(17)。

(17)

分析式(17)可以发现，公式中大括号的部分可用FFT算法实现，这样保证了计算效率，也提高了计算精度。由于不用计算零波数，避免了零波数造成的奇异问题。但是Gauss-FFT需要用Mx·My次FFT，时间代价增大，可用通过采用并行计算技术解决。

在实际解决具体的复杂地质体的重力异常三维正演时，实现本方法的具体流程如下：

1)给定剖分区域，确定剖分棱柱体个数Nx、Ny、Nz，水平方向均匀剖分，垂直方向可可非均匀剖分；在研究含有起伏地形的情况时，起伏地形要完全包含在剖分区域内；给定Gauss-FFT反变换时高斯点个数Mx、My，高斯坐标ta、tb和高斯系数Aa、Ab。

2)根据地质体密度分布给每个剖分的小棱柱体的剩余密度进行赋值。

4)根据式(16)，利用FFT算法计算密度波数域值。

6)利用式(17)和FFT算法，计算空间域重力异常。

7)计算起伏观测面(图2)或者起伏地形(图3)上的重力异常时，采用如下策略。

采用步骤1)～步骤7)的方法，计算起伏观测面最高点和最低点之间的多个平面的异常值，然后采用三次样条差值方法，插值得到起伏观测面上的场值。

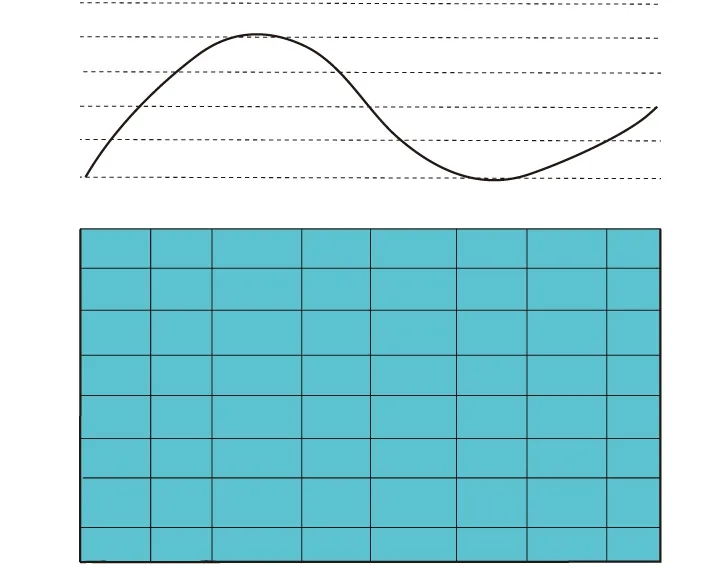
图2 起伏观测面和插值平面示意图Fig.2 Rugged observation surface and interpolation planes

图3 起伏地形和插值平面示意图Fig.3 Rugged topography and interpolation planes

3 模型算例

为了检验笔者提出的算法在解决任意密度分布情况下复杂地质体重力异常三维正演问题的计算速度和计算精度，设计了棱柱体异常模型，分别计算平面和起伏面上的重力异常值。两种观测面上的重力异常都可通过解析公式计算得到，用笔者提出的算法计算得到的重力异常数值解与解析解进行对比，以此验证算法的计算精度,并用式(18)给出的均方误差进行衡量。

(18)

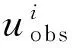
模型的剖分区域：x方向-1 000 m～1 000 m,y方向-1 000 m～1 000 m,z方向0 m～500 m；棱柱体异常的位置为：x方向-300 m～300 m,y方向为-300 m～300 m,z方向100 m～300 m；围岩密度均为0 kg/m3，棱柱异常体密度为1 000 kg/m3；高斯FFT算法中x方向和y方向选用高斯点均为4个。

笔者提出的数值算法均用Fortran语言实现，并在CPU主频2.80GHz、内存为32GB的个人笔记本电脑运行。

3.1 重力异常

图4显示了观测面z=0 m 的平面重力异常均方误差和计算时间随棱柱体剖分个数的变化，从图中可以看出，计算精度随着剖分个数的增加越来越高，达到一定的剖分个数时，计算精度提高缓慢；计算时间随剖分个数的增加而增多，在剖分为100*100*100时，均方根误差为0.000 13 mGal，计算时间约为1.3 s,计算效率高。两条曲线的交点可认为是计算精度与计算时间之间一个很好的折中点，所对应的剖分个数可认为是最佳剖分个数。本算例中最优的剖分个数约为100*100*50。

图4 均方误差和计算时间随棱柱体剖分个数变化Fig.4 Curves of RMSE and calculation time with the varied number of subdivided prisms

图5和图6分别给出的是剖分个数为100*100*50时，z=0 m平面重力异常的解析解和数值解。对比图5与图6，两者形态几乎一致，解析解与数值解作差，误差如图7所示。从图7中可看出，总体误差很小(误差与解析解相差3个～4个)，相比采用传统FFT的波数域方法，笔者基于Gauss-FFT法的波数域方法边界误差很小，具有很高的计算精度。

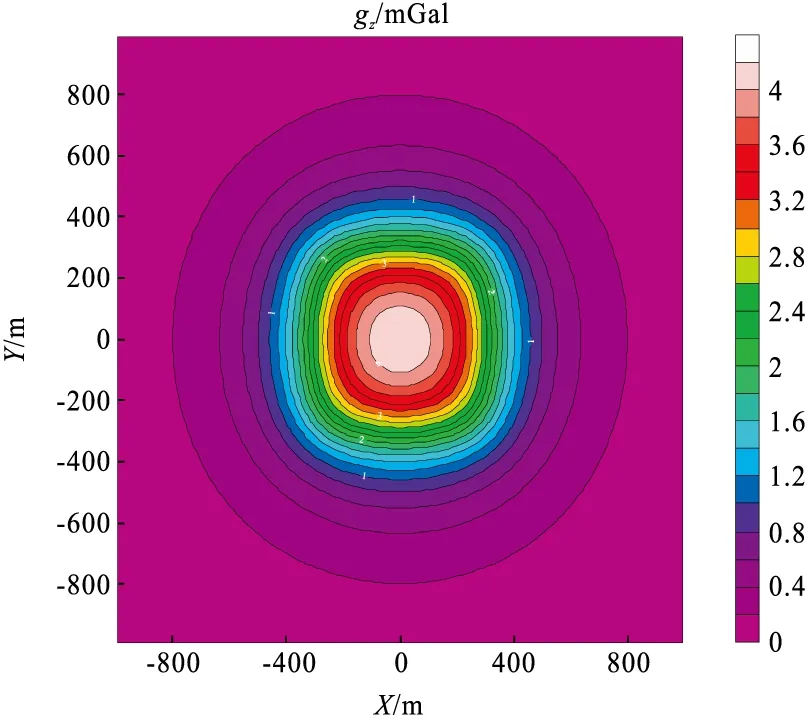
图5 平面重力异常解析解Fig.5 Analytical solution of gravity anomalies on a plane

图6 平面重力异常数值解Fig.6 Numerical solution of gravity anomalies on a plane

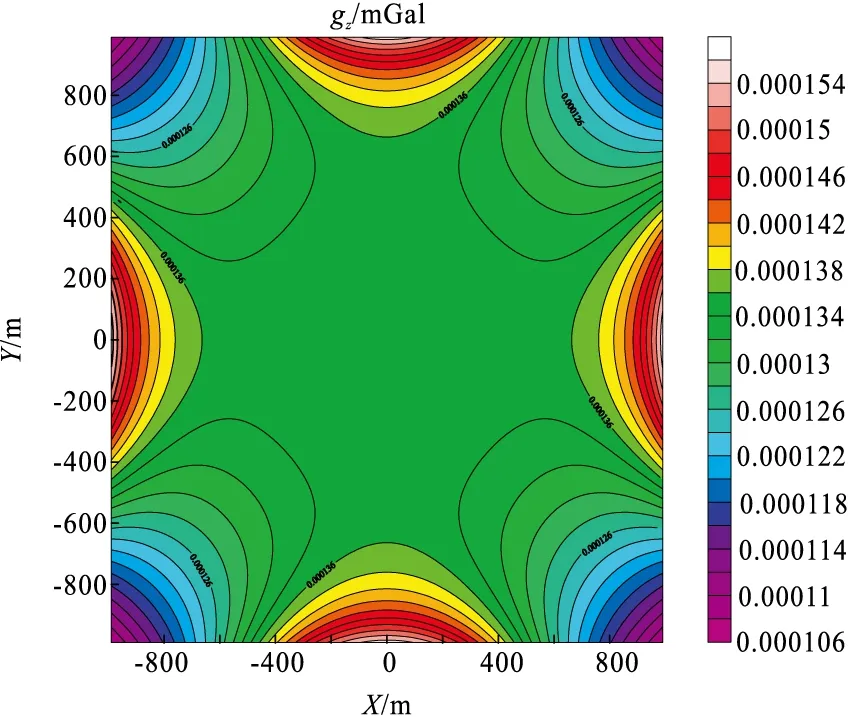
图7 平面重力异常误差图Fig.7 Computation errors of gravity anomalies on a plane

图8 起伏观测面Fig.8 Rugged observation surface

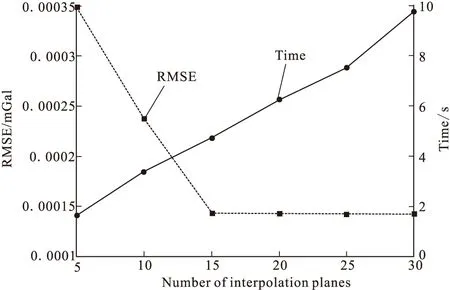
图9 均方误差和计算时间随插值平面个数变化图Fig.9 Curves of RMSE and calculation time with the varied number of interpolation planes

3.2 观测重力异常

如图8所示，笔者采用简化的起伏观测面，该观测面由z=-100 m、z=0 m 、 z=100 m三个平面组合而成，插值平面在z=-110 m～110 m之间。

图9显示了模型剖分个数为100*100*50时，起伏观测面的重力异常均方误差和计算时间随差值平面个数的变化，从图9中可以看出，计算精度随着剖分个数的增加而提高，但当插值平面个数达到一定时，计算精度几乎不变；同时，计算时间随插值平面个数的增加逐渐增多，在插值平面为15个时，均方根误差为0.000 14 mGal，计算时间约为4.7 s,计算效率高。两条曲线的交点可认为是计算精度与计算时间之间一个很好的折中点，所对应的插值平面个数可认为是最佳个数。本算例中最优的插值平面个数约为15。

当插值平面个数为10时，图10和图11分别给出起伏观测面上重力异常的解析解和数值解。对比图10与图11，两者形态几乎一致，解析解与数值解作差，误差如图12所示。从图12中可看出，总体误差很小(误差与解析解相差3个～4个数量级)，大的误差主要集中在异常体区域以及起伏观测凹凸面的边界，说明了本文算法在计算起伏观测面的重力异常时也具有很高的精度。对比图11和图6可以看出，起伏地形上的重力异常比起平面上的场存在变化，在起伏凹凸面上变化形态明显，凹面的异常值变大，凸面的异常场变小。

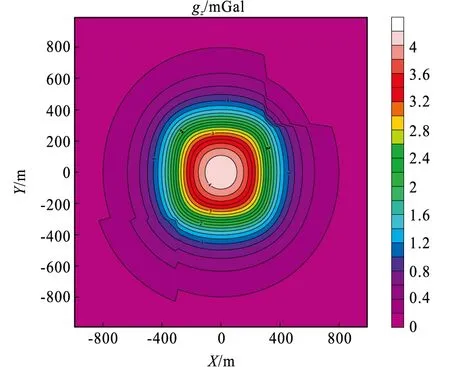
图10 起伏观测面重力异常解析解Fig.10 Analytical solution of gravity anomalies on a rugged surface

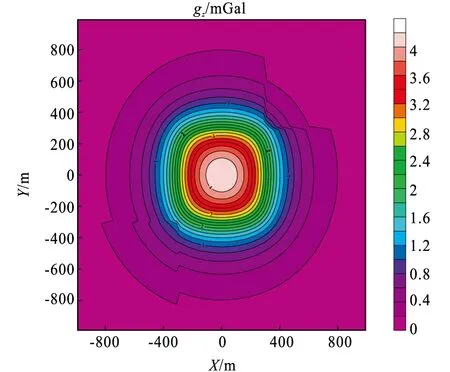
图11 起伏观测面重力异常数值解Fig.11 Numerical solution of gravity anomalies on a rugged surface

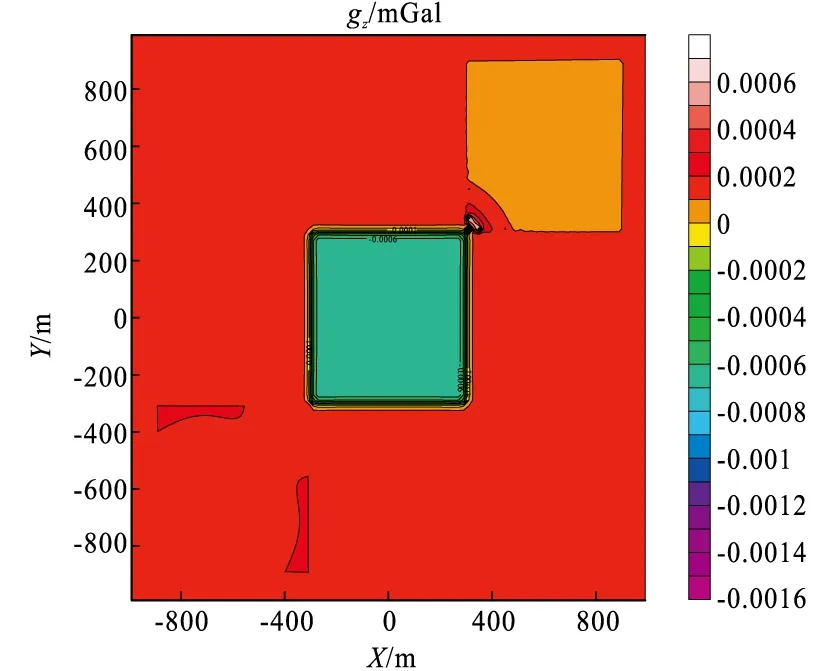
图12 起伏观测面重力异常误差图Fig.12 Computation errors of gravity anomalies on a rugged surface

4 结论

针对任意密度分布复杂地质体重力异常正演问题，笔者提出一种基于高斯FFT法的波数域算法，在数值实现过程中，采用了Gauss-FFT法，保证计算效率的同时，有效克服了传统FFT法引起的边界效应和零波数点的奇异问题。

笔者提出的算法对于剖分规模为128*128*64的算例，观测点为128*128个时，在CPU主频为1.90 GHz、内存为4 GB的电脑上运行的计算时间约为38 s。笔者提出的算法的计算速度在没有并行的前提下，在主频更低的计算机上的计算速度，比前人提出的方法[16]快了约2.6倍。由此可以说明我们提出的算法速度快，精度高。此外，本算法具有很好的并行性，结合并行计算技术，可以进一步提高本方法的计算效率，特别适合应用于三维重力反演和人机交互建模。

[1] CAI Y,WANG C.Fast finite-element calculation of gravity anomaly in complex geological regions [J].Geophysical Journal of International,2005,162:696-708.

[2] C G FARQUHARSON, C R W MOSHER. Three-dimensional modelling of gravity data using finite differences[J]. Journal of Applied Geophysics, 2009, 68(3): 417-422.

[3] MAY D A, KNEPLEY M G. Optimal, scalable forward models for computing gravity anomalies[J]. Geophysical Journal International, 2011, 187(1): 161-177.

[4] JAHANDARI H, FARQUHARSON C G. Forward modeling of gravity data using finite-volume and finite-element methods on unstructured grids[J]. Geophysics, 2013, 78(3): 69-G80.

[5] GUZMAN S. Forward modeling and inversion of potential field data using partial differential equations [D]. MS thesis of Colorado School of Mines, 2015.

[6] 何昌礼, 钟本善. 复杂形体的高精度重力异常正演方法[J]. 物探化探计算技术, 1988,10(2): 121-128. HE C L, ZHONG B S, A high accuracy forward method for gravity anomaly of complex body [J]. Computing Techniques for Geophysical and Geochemical Exploration, 1988，10(2): 121-128.(In Chinese)

[7] TONTINI F C,COCCHI L,CARMISCIANO C.Rapid 3-D forward model of potential fields with application to the Palinuro Seamount magnetic anomaly (southern Tyrrhenian Sea, Italy)[J].Journal of Geophysical Research Solid Earth,2009,114(B2):1205-1222.

[8] WU L Y , TIAN G. High precision Fourier forward modeling of potential fields[J]. Geophysics, 2014, 79(5): G59-G68.

[9] 柴玉璞.偏移抽样理论及其应用[M]. 北京: 石油工业出版社，1997. CHAI Y P.Shift Sampling Theory and its Application[M].Beijing: China Petroleum Industry Press,1997. (In Chinese)

[10]LI Y G, OLDENBURG DW. 3-D inversion of gravity data[J]. Geophysics, 1998, 63(1): 109-119.

[11]ZHDANOV M S, R ELLIS, S MUKHERJEE. Three-dimensional regularized focusing inversion of gravity gradient tensor component data[J]. Geophysics, 2004. 69(4): 925-937.

[12]周宇轩, 雷宛. 重力异常物性正则化反演研究[J]. 物探化探计算技术, 2016,38(5): 579-583. ZHOU Y X, LEI W, Study on physical properties regularization inversion anomaly[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2016,38(5): 579-583. (In Chinese)

[13]XIA H. Interactive modeling of potential fields in three dimensions[J]. SEG Expanded Abstracts of the 63th Annual Meeting,1993:403-404.

[14]吴文鹂, 管志宁, 高艳芳, 等. 重磁异常数据三维人机联作模拟[J]. 物探化探计算技术, 2005, 27(3): 227-232. WU W L, GUAN Z N, GAO Y F, et al, Interactiv man/computer moding 3D body of gravity and magnetic anomaly data[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2005, 27(3): 227-232. (In Chinese)

[15]陈龙伟, 戴世坤, 吴美平. 应用任意采样点数FFT算法时离散频率计算[J]. 地球物理学进展, 2016(1):164-169. CHEN L W, DAI S K，WU M P. Computation of discrete frequency when using FFT algorithm with random sampling points[J]. Progress in Geophysics, 2016(1):164-169. (In Chinese)

[16]徐世浙.地球物理中的有限单元法[M].北京：科学出版社,1994. XU S Z.Finite element method in Geophysics[M].Beijing:Science Press,1994. (In Chinese)

[17]陈召曦, 孟小红, 郭良辉,等. 基于GPU并行的重力、重力梯度三维正演快速计算及反演策略[J]. 地球物理学报, 2012, 55(12):4069-4077. CHEN Z X, MENG X H, GUO L H, et al. Three-dimensional fast forward modeling and the inversion strategy for large scale gravity and gravimetry data based on GPU[J]. Chinese Journal of Geophysics- Chinese Edition, 2012, 55(12):4069-4077.(In Chinese)

第39卷 第2期2017年3月物探化探计算技术COMPUTING TECHNIQUES FOR GEOPHYSICAL AND GEOCHEMICAL EXPLORATIONVol.39 No.2Mar. 2017

Three-dimensional forward modeling method for gravity anomalies of complex geological bodies with arbitrary density distribution

CHEN Qingrui1, CHEN Longwei2, DAI Shikun1, ZHANG Qianjiang1, OUYANG fang1

(1.School of Geosciences and Info-Physics, Central South University, Changsha 410083, China; 2.College of Earth Sciences, Guilin University of Technology, Guilin 541006,China )

Rapid three-dimensional (3D) forward modeling of gravity anomalies of complex geologic bodies with arbitrary density distribution plays an important role on 3D inversion of gravity and human-computer interaction modeling and interpretation. This paper proposes a wavenumber domain 3D forward modeling method. This new method has three key aspects: (1) prism based subdivision strategy. The research area is divided into many small regular prisms, density for each small prism can be given arbitrarily, in order to simulate complex geological body with arbitrary density distribution and undulating topography; (2) new wavenumber domain formula for computing gravity anomaly of combined prism model; (3) Gauss-FFT method. This paper uses Gauss-FFT method to transform the gravity anomaly from the wave number domain to the spatial domain. The Gauss-FFT method not only has high computational efficiency, but also suppresses the boundary effect and avoids the singular problem at zero wavenumber caused by the traditional FFT method. Numerical tests show that the proposed method is fast and accurate. It takes only a few seconds to calculate gravity anomaly for the combined 3D model with millions of prisms.

gravity anomalies; three-dimensional forward modeling; Gauss-FFT; integral equation

2016-11-29 改回日期：2017-01-09

国家自然科学基金项目(41404106)

陈轻蕊(1992-)，女，硕士，从事重磁、电磁数值模拟研究，E-mail：1532550316@qq.com。

陈龙伟(1982-)，男，博士，从事重磁勘探、电磁勘探研究，E-mail：longweichen_glut@glut.edu.cn。

1001-1749(2017)02-0176-07

P 631.1

A

10.3969/j.issn.1001-1749.2017.02.04