流体替换对合成地震记录影响研究

李鹏飞， 黄 诚， 高莲花

(中国石油 塔里木油田分公司勘探开发研究院，库尔勒 841000)

流体替换对合成地震记录影响研究

李鹏飞， 黄 诚， 高莲花

(中国石油 塔里木油田分公司勘探开发研究院，库尔勒 841000)

流体替换是研究流体对岩石弹性参数影响的有利手段，其对于地震属性分析具有重要意义。在构建了四层介质模型的基础之上,基于Gassmann方程对储层进行了流体替换，采用褶积模型，运用matlab语言编程考查了不同孔隙度储层中含有流体时的人工合成地震记录。研究结果表明,当储层孔隙中完全被水替换后，储层上、下两层反射振幅在地震记录上明显增强，在临界孔隙度范围内随着替换孔隙度的增大反射振幅能量减弱，反射振幅变化率变化较小。研究基于流体替换的地震正演响应对于流体识别、储层预测具有借鉴意义。

流体替换； Gassmann方程； 褶积； 地震正演

0 引言

通过岩石物理分析可以将岩石的地质参数和弹性参数关联起来，流体替换是正演模拟及定量化研究分析的辅助手段，同时也为AVO[1]及四维地震勘探研究分析奠定了基础。众所周知，目前油气勘探开发难度越来越大，潜力越来越小，加之随着全球对油气资源需求的不断增长，为了更加精准地进行地震油藏描述，精确地识别不同性质的流体，对流体替换研究进行研究是我们地球物理工作者必须长期坚持的一项工作。

总结前人的研究成果发现流体替换模型众多，比较常用的模型有: Gassmann提出的Gassmann方程[2]; Wyllie[3-4]提出的Wyllie时间平均方程;Biot理论[5]以及K-T模型[6]；Xu等[7]结合微分等效介质理论、K-T模型以及Gassmann[8-9]理论提出了描述砂泥岩混合岩石的Xu-White模型，这些模型是进行流体替换的理论基础。在众多模型中Gassmann方程以其所涉及的物理参数简单明了、参数易于确定、具有明确的物理意义的优点,成为行业中进行流体替换最常用的方程，该方程精确地描述了岩石内孔隙流体对岩石弹性参数的影响。

国内、外众多学者在流体替换方面都做了许多基础实验及研究工作：Kilmentos[10]对岩石孔隙弹性相关参数进行了实验研究;葛洪魁[11]等对砂岩孔隙弹性特征进行了试验研究;李生杰[12]研究分析了在流体替换过程中岩石刚性、孔隙度对岩石弹性参数的影响；王东[13]等对部分孔隙岩石中声波传播规律进行了数值研究分析;Hilterman[14]以oigt-Reuss-Hill经验公式求取岩石固体基质的弹性参数为基础提出了Gassmann方程进行流体替换的具体流程;林凯等[15-16]提出运用Biot理论来求取干岩石的体积模量，进而求取流体替换后的地震属性参数；黄伟传等根据地层含有不同性质的流体时由Gassmann[17]方程推导出了的地层的相关地震弹性参数;云美厚[18]等利用Gassmann方程详细讨论了在储层条件下计算砂岩纵、横波速度。

在前人的研究基础之上，笔者构建了四层介质模型，基于Gassmann方程对储层进行了流体替换工作，采用褶积模型[19]，借助matlab强大数学计算和图像可视化功能，观察了不同孔隙度储层中含有流体时的人工合成地震记录[20-22]，希望本研究对于流体识别、储层预测具有借鉴意义。

1 流体替换

1.1 Gassmann方程

Gassmann提出了Gassmann方程，它一直是岩石物理研究工作者的强有力工具。在低频条件下Gassmann方程与Biot理论的结果相同，对该公式的推导主要是根据文献[2]，同时也可根据Biot理论或功的互等定理推导出[23]。

在提出Gassmann方程时是建立在以下5点假设条件之上的：①岩石(基质和骨架)宏观上是均质的(孔隙大小远小于地震波波长)；②全部孔隙是相互连通的；③孔隙里面全部充满流体(气、油、水或混合物);④岩石-流体系统不与外界相通，是封闭的(不排液)；⑤孔隙流体对固体骨架不产生相互作用(软化或硬化)。推导出的Gassmann方程的基本形式为：

(1)

ρ=φρf+(1-φ)ρm

(2)

其中：K表示岩石的等效体积模量；u表示岩石的等效剪切模量；Kd表示岩石骨架(干燥岩石)体积模量；ud表示岩石骨架(干燥岩石)剪切模量；Km表示岩石骨架(干燥岩石)中岩石基质的体积模量；Kf表示孔隙流体的体积模量；φ表示岩石孔隙度;ρ表示岩石等效密度；ρf表示孔隙流体密度；ρm表示岩石基质密度；

从式(1)中可以看出，Gassmann理论认为岩石的体积模量会随着空隙流体的改变而改变，而岩石剪切模量保持不变。

1.2 流体替换流程

流体替换过程大致可分为三类：①干岩石替换成有空隙的饱和流体岩石；②在孔隙度一定的情况下岩石由饱和状态1替换成饱和状态2；③变孔隙度情况下岩石由饱和状态1替换成饱和状态2。笔者仅采用第一类流体替换过程，着重考查流体替换后的合成地震记录的变化情况，具体的流体替换流程见图1。

图1 流体替换流程Fig.1 Fluid substitution flow

2 正演原理简述

简单的正演模拟是对实际复杂介质作适当简化，一般简化为均匀介质或水平层状介质，然后用数学或物理方法研究地震波的传播规律。地震正演模拟有助于指导野外采集及室内处理、解释等研究工作。

我们知道对于垂直入射的地震波，其波阻抗z=ρ*v，反射系数r=(zn+1-zn)/(zn+1+zn)，其中，ρ表示介质密度，v表示介质速度，zn表示第n层介质波阻抗，zn+1表示第n+1层介质波阻抗。根据褶积理论，在时间域地震中，如果用w(t)表示地震子波，r(t)表示反射系数，地震子波及反射系数均为时间t(双程垂直反射时间)的函数，那么t时刻的合成地震记录即地震道振幅f(t)可表示为式(3)。

f(t)=w(t)*r(t)

(3)

3 算例

笔者构建了四层介质模型，其模型参数具体设置见图2。基于Gassmann方程对第二层介质进行了流体(水)替换工作，第二层介质临界孔隙度设为0.4，水体积模量kwater=3.013 Gpa,密度ρwater=1.0 g/cm3，孔隙度φ=5%及25%，替换时都视为100%含水。正演计算时采用褶积模型，地震子波选用雷克子波，主频为50 Hz,采样间隔为0.001 s，采样点数为100。计算结果如图3～图4所示。从图3～图4中可以清楚看出：在未进行流体替换时，第一、二层反射界面振幅能量较弱，第三层反射界面振幅能量较强；当对第二层介质进行空隙度为5%、25%的流体(水)替换后，第一、二层反射界面振幅能量明显增强。不同孔隙度流体(水)替换后的合成地震记录差别如表1所示，从表1中可以清楚看到：未进行流体替换时，第一层反射界面最大振幅为0.015；进行孔隙度为5%的流体替换后，第一层反射界面最大振幅变为0.219；进行孔隙度为25%的流体替换后，第一层反射界面最大振幅变为0.185。为了定量化研究孔隙度对合成地震记录影响，笔者还进行了孔隙度为15%、35%的流体替换工作，绘制了最大振幅强度随替换孔隙度变化的关系曲线(图5)。图5中黑线代表替换孔隙度φ与发射界面最大振幅值的对应关系，对该关系曲线进行线性拟合(图中红线)发现：曲线斜率为-0.001，在临界孔隙度范围内，随着替换孔隙度的增大替换层上反射界面振幅能量减弱，且其振幅变化率基本保持不变。替换层下反射界面振幅变化情况与上层相似。

图2 四层介质模型Fig.2 Four layer medium model

图3 未进行流体替换合成地震记录Fig.3 Synthetic seismic record

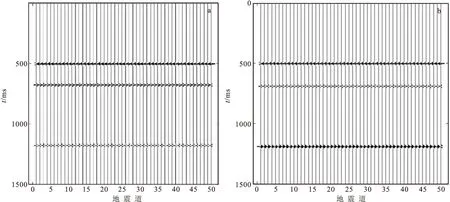
图4 流体替换后合成地震记录Fig.4 Synthetic seismic record after fluid substitution(a)φ=5%;(b)φ=25%

未进行流体替换ϕ=25%替换ϕ=5%替换第一层反射界面最大振幅0.0153850.1852530.218801第二层反射界面最大振幅0.0322580.138860.17298

图5 替换孔隙度与最大振幅关系Fig.5 Relationship of porosity and maximum amplitude

4 结论

通过对建立的四层介质模型进行流体(水)替换及地震正演模拟，考查流体(水)替换前后的合成地震记录发现：对第二层介质进行流体替换后，该层介质上、下反射界面振幅能量明显增强；在临界孔隙度范围内，流体替换时随着孔隙度增大，反射界面振幅能量减弱，且振幅变化率基本保持不变。

笔者是在建立的四层介质模型基础之上，只选择了一种性质流体(水)进行流体替换得出的相关结论，具有一定局限性。但是笔者认为流体替换前、后的这种合成地震记录的变化，是正确识别流体性质及储层的重要前提，在地震解释时需要慎重思考该问题，希望通过本次地研究对于流体识别、储层预测具有借鉴意义。笔者在以后的学习研究中尚需进行许多其他的研究工作，如使用其他性质流体(油、气等)进行流体替换工作；进行不同饱和度的流体替换及从一种流体状态到另一种流体状态的替换等工作。

[1] FRED J，HILTERMAN.Seismic amplitude interpretation. houston[C].SEG / EAGE Short Course No.4, 2001.

[2] WYLLIE M R J, GREGORY A R ，GARDNER L W. Elastic wave velocities in heterogeneous and porous media[J].Geophysics,1956,21(1):41-70.

[3] WYLLIE M R J. An experimental investigation of factors affecting elastic wave velocities in porousmedia[J].Geophysics,1958, 23(3): 459-493.

[4] GASSMANN F. Elastic waves through a peaking of spheres[J]. Geophysics, 1951,16:673-685.

[5] BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid,Ⅰ: Low frequency range[J]. The Journal of the Acoustic Society of America, 1956, 28(2):168-178.

[6] BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid,Ⅱ: Higher frequency range[J]. The Journal of the Acoustic Society of America, 1956, 28(2):179-191.

[7] GASSMANN F. Uber die elastizitat poroser medien [J]. Veir. Der Nater Gesellschaft [R], 1951, 96: 1-23.

[8] XU S, WHITE R E. A new velocity model for clay-sand mixtures [J]. Geophysical Prospecting, 1995, 43(1): 91-118.

[9] XU S, WHITE R E. A physical model for shear-wave velocity prediction [J].Geophysical Prospecting, 1996, 44(4): 687-717.

[10]KILMENTOS T, HAROUAKA A, MTAWAA B, et al. Experimental determination of the biot elastic constant: applications in formation evaluation ( sonic porosity, rock strength, earth stress and standing predictions)[R]. Spe Reservoir Evaluation & Engineering, 1998, 1(1):57-63.

[11]葛洪魁,韩德华,陈颙.砂岩孔隙弹性特征的试验研究[J].岩石力学与工程学报, 2001, 20(3): 332-337. GE H K, HAN D H, CHEN Y. Experimental investigation on poroelasticity of sandstones[J]. chinese journal of rock mechanics and engineering,2001, 20(3): 332-337.(In Chinese)

[12]李生杰. 岩性、孔隙及其流体变化对岩石弹性性质的影响[J].石油与天然气地质, 2005, 26(6): 760-764. LI S J. Influence of lithology, porosity and variation of pore fluid saturation on rock elastic property[J]. Oil & Gas Geology, 2005, 26(6): 760-764.(In Chinese)

[13]WANG D, ZHANG H l, WANG X M. A numerical study of acoustic Wave propagation in partially saturated poroelastic rock[J]. Chinese Journal of Geophysics, 2006, 49(2): 524-532.

[14]HILL R W. The elastic behavior of crystalline aggregate[J]. Proceedings of Physical Society, section A,1952, 65(5):349-354.

[15]林凯,贺振华，熊晓军，等.基于Gassmann方程的流体替换流程[J].长江大学学报(自然科学),2009,6(1):180-181. LIN K, HE Z H,XIONG X J,et al. Based on the Gassmann Equation Fluid Substitution Flow[J].Journal of Yangtze University ( Nat Sci Edit), 2009,6(1):180-181.(In Chinese)

[16]林凯.基于Gassmann方程的鲕滩储层流体替换模拟技术及其应用[J].石油物探,2009,48(5): 493-498. LIN K. Fluid substitution simulation technology based on Gassmann’s equation for oolitie shoal reservoir and its application[J].Geophysical prospecting for petroleum, 2009,48(5): 493-498.(In Chinese)

[17]HUANG WC，YANG CC，FAN TY，et al .The application of petrophysical analysis in the reservoir prediction[J]. Progressing Geophysics, 2007, 22(6):1791-1795.

[18]YUN M H,GUAN Z Y.The estimation of PandS wave velocities in Sand stone under the in-situ conditions [J].Geophysical prospecting for Petroleum,2002,41(3):289-293.

[19]朱青奇, 刘英. 基于褶积理论的地震模型分析与探讨[J].石油地质与工程, 2012, 26(2)：20-23. ZHU QINGQI, LIU YING. Analysis and Discussion on seismic model based on convolution theory[J].Petroleum geology and engineering,2012, 26(2)：20-23.(In Chinese)

[20]刘卫国. MATLAB程序设计教程[M]. 北京：水利水电出版社,2005. LIU W G. MATLAB programming tutorial[M]. Bei jing: China WaterPower Press, 2005. (In Chinese)

[21]黎华.地形与地质体三维可视化的研究与应用[D].广州：中国科学院研究生院(广州地球化学研究所),2006. NI H. Research and application of 3D visualization of terrain and geological body[D]. Guangzhou: Geochemical Research Institute, 2006. (In Chinese)

[22]杨永亮, 庚琪. 三维地质建模软件对比研究[J].石油工业计算机应用,2008(1):16-19. YANG Y L, GENG Q. The comparative study of three-dimensional geological modeling software[J]. Computer Applications Of Petroleum, 2008(1):16-19. (In Chinese)

[23]MAVKO.岩石物理手册-空隙介质中的地震分析工具[M].北京:中国科学技术大学出版社, 2008. MAVKO. The Rock Physics Handbook-tools for seismic analysis in porous Media[M]. Bei Jing: Press of University of Science and Technology of China, 2008.(In Chinese)

Synthetic seismic record research based on fluid substitution

LI Pengfei, HUANG Cheng, GAO Lianhua

(Research Institute of Exploration and Development,Tarim Oilfield Company,PetroChina, Korla 841000， China)

Fluid substitution is powerful way to study effect of fluids on elastic parameters of rock. It is of great significance for the seismic attribute analysis. In this paper, the reservoir fluids replacement was made by Gassmann equation based on four layer medium model constructed. It applies convolution model to check synthetic seismic record of different porosity reservoir by matlab language programming. The results show that: the reflection amplitude of upper and lower layers enhanced obviously if reservoir pore was completely replaced by water; the influence of the porosity was little. It is important guidance and reference significance for fluid identification and reservoir prediction to research on seismic forward modeling response of fluid substitution.

fluid substitution; Gassmann equation; convolution; seismic forward

2016-04-04 改回日期：2016-06-07

李鹏飞(1990-)，男，硕士，主要从事物探解释、岩石物理研究，E-mail：295196232@qq.com。

1001-1749(2017)02-0243-05

P 631.4

A

10.3969/j.issn.1001-1749.2017.02.14