基于改进SDRE非线性鲁棒控制的二元机翼颤振抑制

苟义勇， 李洪波， 董新民， 杨任农， 左仁伟

(空军工程大学 航空航天工程学院，西安 710038)

基于改进SDRE非线性鲁棒控制的二元机翼颤振抑制

苟义勇， 李洪波， 董新民， 杨任农， 左仁伟

(空军工程大学 航空航天工程学院，西安 710038)

为有效抑制二元机翼颤振现象，采用Lyapunov稳定性理论设计了一种改进状态相关黎卡提方程(SDRE)的非线性鲁棒控制律。将含前/后缘双控制面的二元机翼模型以状态空间形式描述并将该模型转化成输入矩阵B为行满秩的形式，进而解决了基于SDRE的非线性控制方法不能直接应用于二元机翼颤振主动抑制的问题。仿真结果表明，在阵风干扰和控制面存在偏转角限制的情况下，闭环系统能快速达到稳定状态，颤振现象得到有效抑制。通过调节权重矩阵Q和R，能够减小控制输入幅值。

二元机翼；非线性鲁棒控制；颤振；状态相关黎卡提方程

由于空气动力、弹性力和惯性力的相互作用，飞行器普遍存在颤振现象[1]。颤振会使得飞行性能与作战性能受到严重限制,甚至对飞行安全产生严重的影响。因此对颤振现象进行主动抑制具有十分重要的现实意义。

XIANG等[2]总结了最近几年非线性气动弹性系统分析和控制方法，把非线性气动弹性问题分为基于大展弦比机翼、全机和二元机翼的三类气动弹性研究问题。在大展弦比机翼气动弹性研究方面，主要集中在对非线性气动弹性结构建模与不稳定气动建模。在全机的气动弹性研究方面，主要集中在对高空长航时飞机和战斗机的非线性气动弹性现象分析。在二元机翼气动弹性研究方面，美国德州农工大学已经搭建起研究气动弹性现象的实验平台，建立了包含结构非线性的气动弹性系统数学模型，并针对该模型设计了大量基于后缘单控制面的控制方法[3-6]，单控制面布局的二元机翼控制效率并不是很高，为提高控制效率，基于前/后缘双控制面的控制方法也得以应用[7-10]。基于SDRE(状态相关Riccati方程)非线性控制方法在颤振主动抑制上已较早得以应用，主要是针对单控制面布局的二元机翼颤1振进行控制；值得注意的是，SDRE非线性控制理论的应用存在限制条件，SDRE方法并不能直接应用在文献[5-6]的二元机翼模型上，原因在于文献[5-6]的二元机翼模型的输入矩阵是一个列向量，而SDRE非线性控制理论要求输入矩阵必须为行满秩矩阵才能确保系统收敛[11]，因此现有文献中基于SDRE的非线性颤振主动抑制方法尚待商榷。

为解决上述问题，本文以前/后缘双控制面布局的二元机翼为研究对象，应用Lyapunov稳定性理论设计了一种改进SDRE非线性鲁棒控制律，实现了二元机翼颤振的有效抑制，本研究旨在为改进SDRE非线性鲁棒控制方法的应用提供理论依据，同时为抑制机翼颤振现象提供可行的新方法。

1 双控制面二元机翼气动弹性模型

本文采用前/后缘双控制面布局的二元机翼气动弹性模型，其模型结构如图1所示。

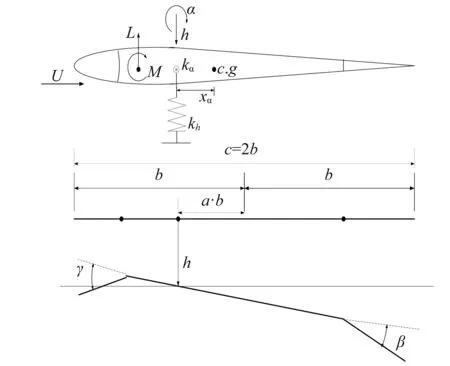
图1 双控制面二元机翼Fig.1 Airfoil with two control surfaces

前/后缘双控制面布局的二元机翼数学模型可表示为

(1)

式中：h为沉浮位移，α为机翼迎角，Iα为机翼惯性矩，xα为机翼重心到弹性轴的距离，kα(α)和kh(h)分别为俯仰方向与沉浮方向所含的非线性刚度，cα和ch分别为俯仰方向和沉浮方向的结构阻尼系数；用准定常理论描述作用在二元机翼上的力矩和气动力，具体可表示为

(2)

式中：ρ为空气密度，sp为机翼翼展长度，U为来流空气速度，b为机翼弦长的一半距离；Clα、Clβ和Clγ分别为机翼迎角、机翼后缘控制面和前缘控制面所产生的升力系数；Clα、Clβ和Clγ分别为机翼迎角、机翼后缘控制面和前缘控制面所产生的升力系数；Cmα-eff、Cmβ-eff和Cmγ-eff分别为相应的有效力矩系数，具体可表示为

(3)

Cmα可视为0。

在模型中加入阵风扰动，由其引起的升力和力矩可表示为

(4)

俯仰方向与沉浮方向所含的非线性刚度kα(α)和kh(h)可分别用多项式拟合为

(5)

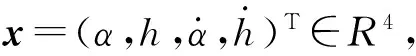
(6)

式中，

F=mtIα-(mwxαb)2,k1=Iαkh(h)/F

k2=(IαρbClαsp+mwxαρspb3Cmα)/F

k3=-mwxαbkh(h)/F

k4=-(mtρspb2Cmα-eff+mwxαρspb2Clα)/F

c1=[Iα(ch+ρspbUClα)+mwxαρcα]/F

c2=[Iαρspb2UClα(0.5-a)-mwxαb+

mwxαρUspb4Cmα-eff(0.5-a)]/F

c3=[mwxαb(ch+ρspbUClα)-mtρUspb2Cmα-eff]/F

c4=mt{[cα-ρUspb3Cmα-eff(0.5-a)]-

mwxαρspb3Clα(0.5-a)}/F

b13=(IαρbClβsp-mwxαρspb3Cmα-eff)/F

b14=(mwxαρspb2Clβ+mtρspb2Cmα-eff)/F

b23=(IαρbClγsp-mwxαρspb3Cmγ-eff)/F

b24=(mwxαρspb2Clγ+mtρspb2Cmγ-eff)/F

式(4)、(6)中的ωg(τ)为气动弹性系统中加入的阵风干扰，该阵风模型为

(7)

考虑前缘和后缘舵面偏转的工作情况，实际的控制输入ui满足：

(8)

(9)

2 改进SDRE非线性鲁棒控制律设计

2.1 模型转换

二元机翼颤振抑制的目的在于使沉浮位移h和机翼迎角α都快速收敛到零。值得注意的是式(6)中输入矩阵B∈R4×2，并不是行满秩矩阵，为了使系统输入矩阵B满足行满秩要求，定义

(10)

对上式求导可得

(11)

定义

x=Zxr

Z=[kBBTξ-A(x)]-1BG0-1

(12)

且，G0=C[kBBTξ-A(x)]-1B,kBBTξ-A(x)为Hurwitz矩阵。

则式(11)可表示为

(13)

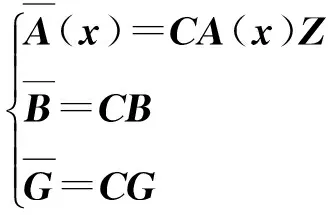
所以式(6)的二元机翼气动弹性模型可表示为

(14)

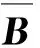
2.2 SDRE鲁棒控制律设计

在非线性系统中考虑最优控制问题，引入目标函数：

(15)

式中，对所有xr=(α,h)T∈R2，R(xr)和Q(xr)都是定义的正定对称矩阵；恰当选择权重矩阵R(xr)和Q(xr)，会得到期望的闭环系统响应。

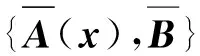
定义一个状态相关黎卡提方程

(16)

式中，K为负定对称矩阵，Q为正定对称矩阵。

根据最优控制思想可设计控制律为

u=L(xr)xr

(17)

(18)

矩阵P(xr)决定了系统稳定性，R为正定对称矩阵，根据式(16)，则需设计参数矩阵K，由于K为负定对称矩阵，则定义

K=-DDT

(19)

其中矩阵D为非奇异矩阵，则式(16)可改写成

(20)

定义一个李亚普诺夫函数

(21)

式中，q=D-1xr。对李亚普诺夫函数式(21)求导可得

(22)

式中,

(23)

定义

(24)

由式(22)、(23)和(24)可知

(25)

引入mori下界[12]:

(26)

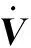
(27)

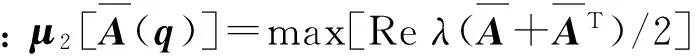
根据mori下界的性质[13]可知

(28)

(29)

(30)

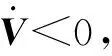
设计参数矩阵为

(31)

则

(32)

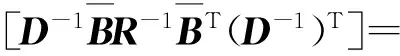
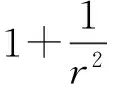
(33)

综上所述，整个闭环系统的结构图如图2所示。

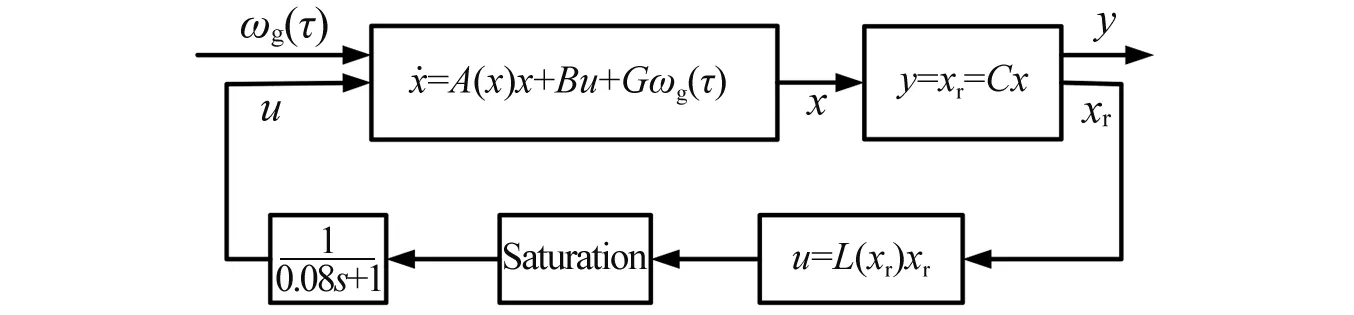
图2 控制系统结构图Fig.2 The structure of control system

3 仿真分析

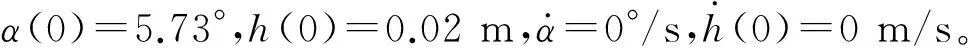
对模型进行线性化处理后发现，模型的稳定性取决于来流速度U；当时U=11.32 m/s，模型的特征值分别为±12.77i，-1.49±12.34i即线性模型存在一对纯虚根。当U≥11.32 m/s时，系统是不稳定的，当U≤11.32 m/s时，系统是稳定的。当速度U=13.20 m/s时，系统的相轨迹如图3所示。

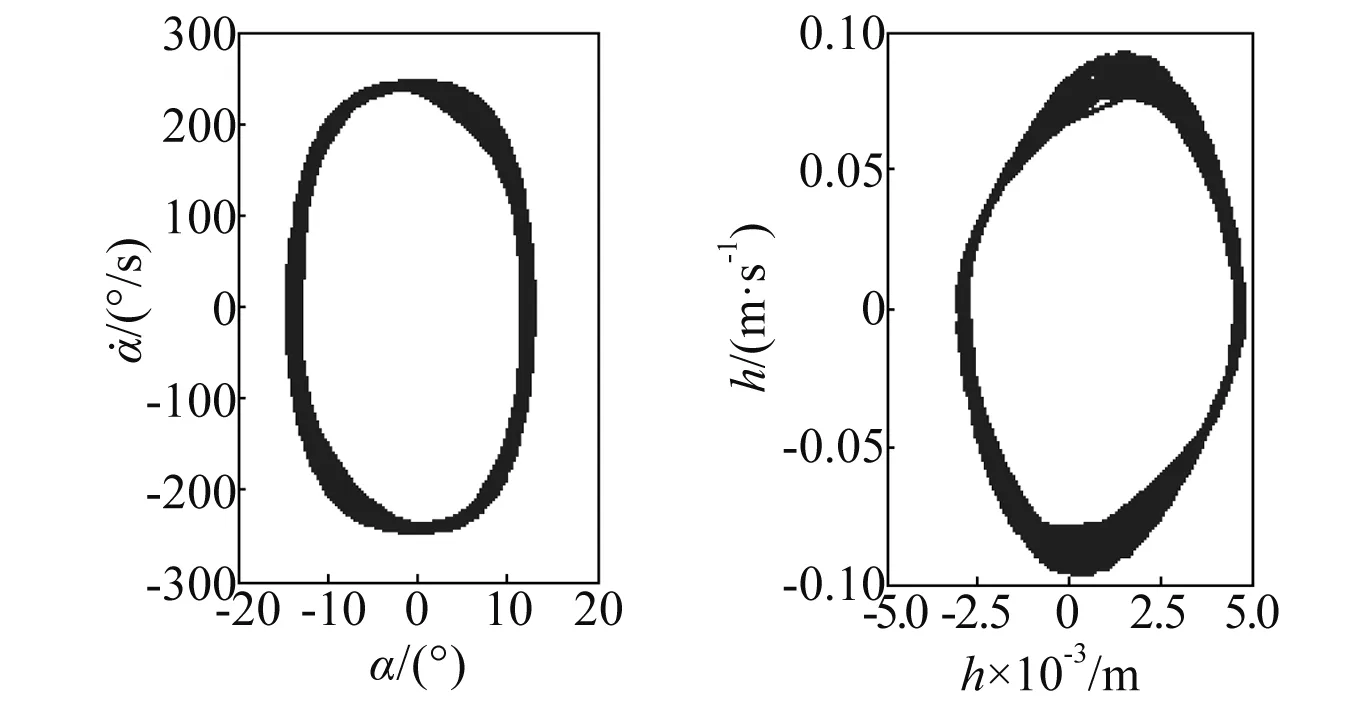
图3 系统相轨迹Fig.3 System phase diagrams

由图3可知，系统出现明显的极限环现象，俯仰运动的幅值为11.32°，沉浮运动的幅值为0.004 8 m。系统颤振的频谱分析如图4所示，可知系统的主要频率成分为2.031 Hz。研究U=13.20 m/s速度下，利用主动控制技术来抑制气动弹性系统的颤振问题。

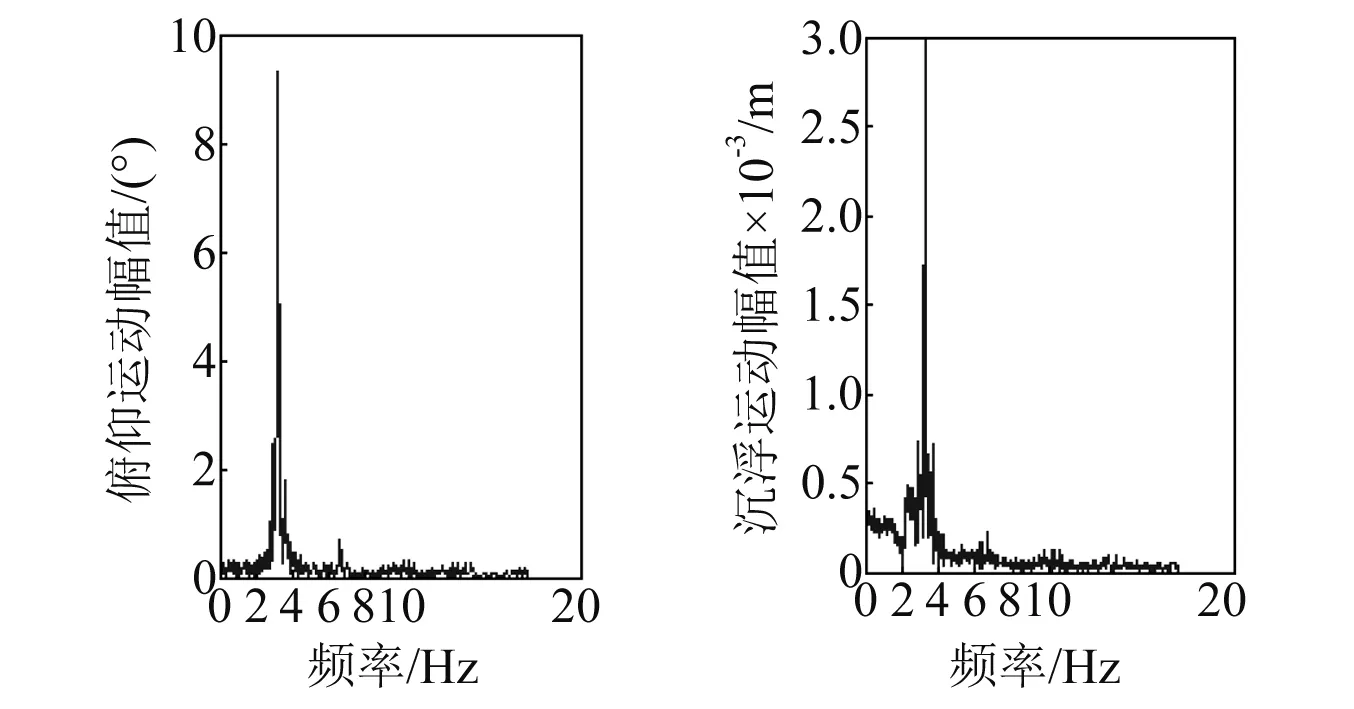
图4 系统频谱Fig.4 System frequency spectra

取来流速,U=13.20 m/s，Q=diag(1,10)，R=diag(10 000,500)，r=1 000，νimax=15°时，νimin=-15°假设阵风干扰在整个仿真过程中始终存在，系统仿真结果如图5所示。

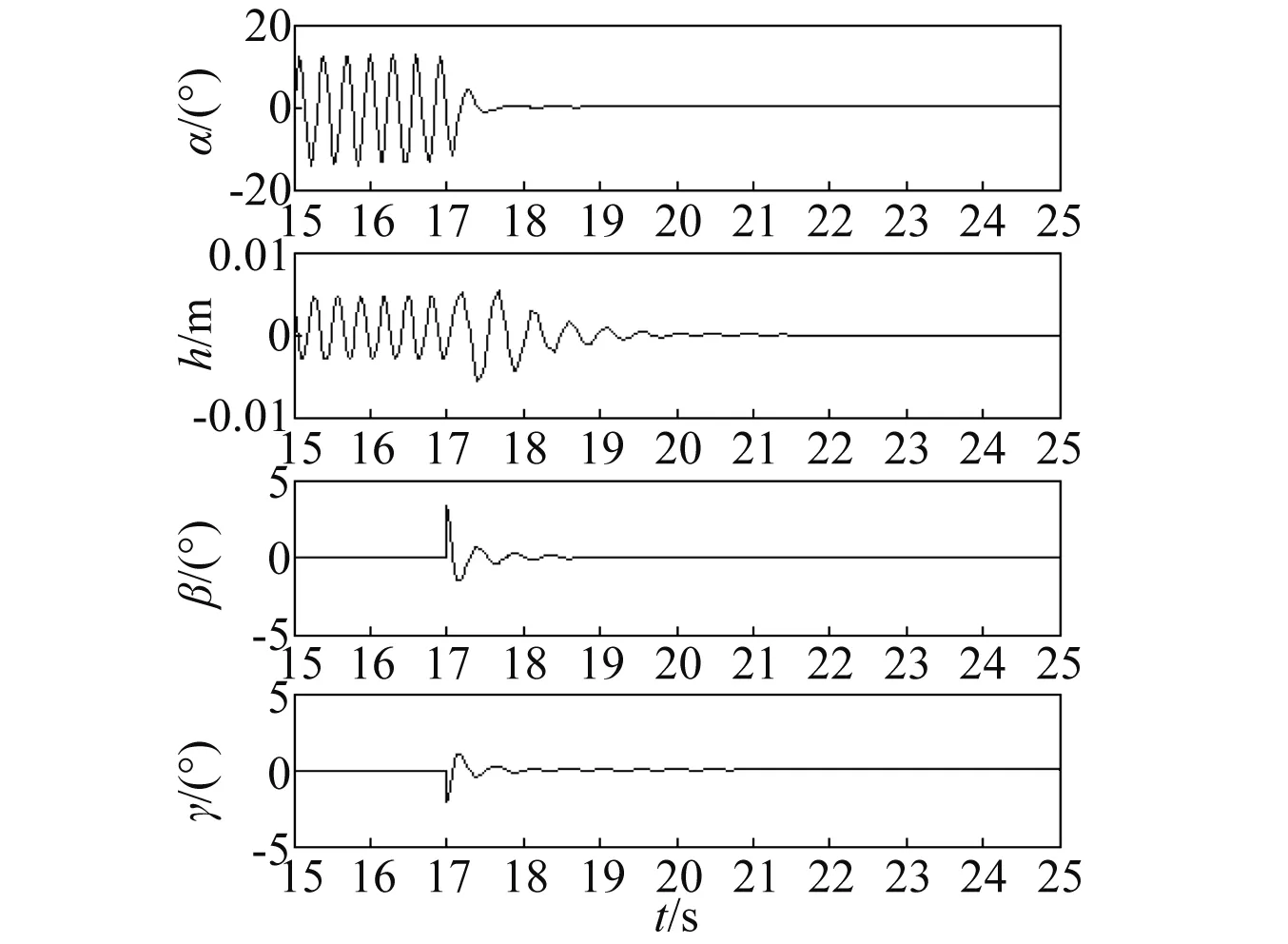
图5 SDRE非线性鲁棒控制 (Q=diag(1,10)，R=diag(10 000,500)，r=1 000)Fig.5 SDRE nonlinear robust control (Q=diag(1,10)，R=diag(10 000,500)，r=1 000)

由图5可知，当t<17 s时，系统发生颤振，其幅值稳定在某一特定值，系统控制输入为0，即此时为系统的开环响应。当t≥17s时，闭环系统能快速达到稳定状态，且前/后缘控制面偏转角都小于10°。

其他仿真条件不变，分别改变Q=diag(10,100)和R=diag(10 000,200)，系统仿真结果分别如图6和图7所示。

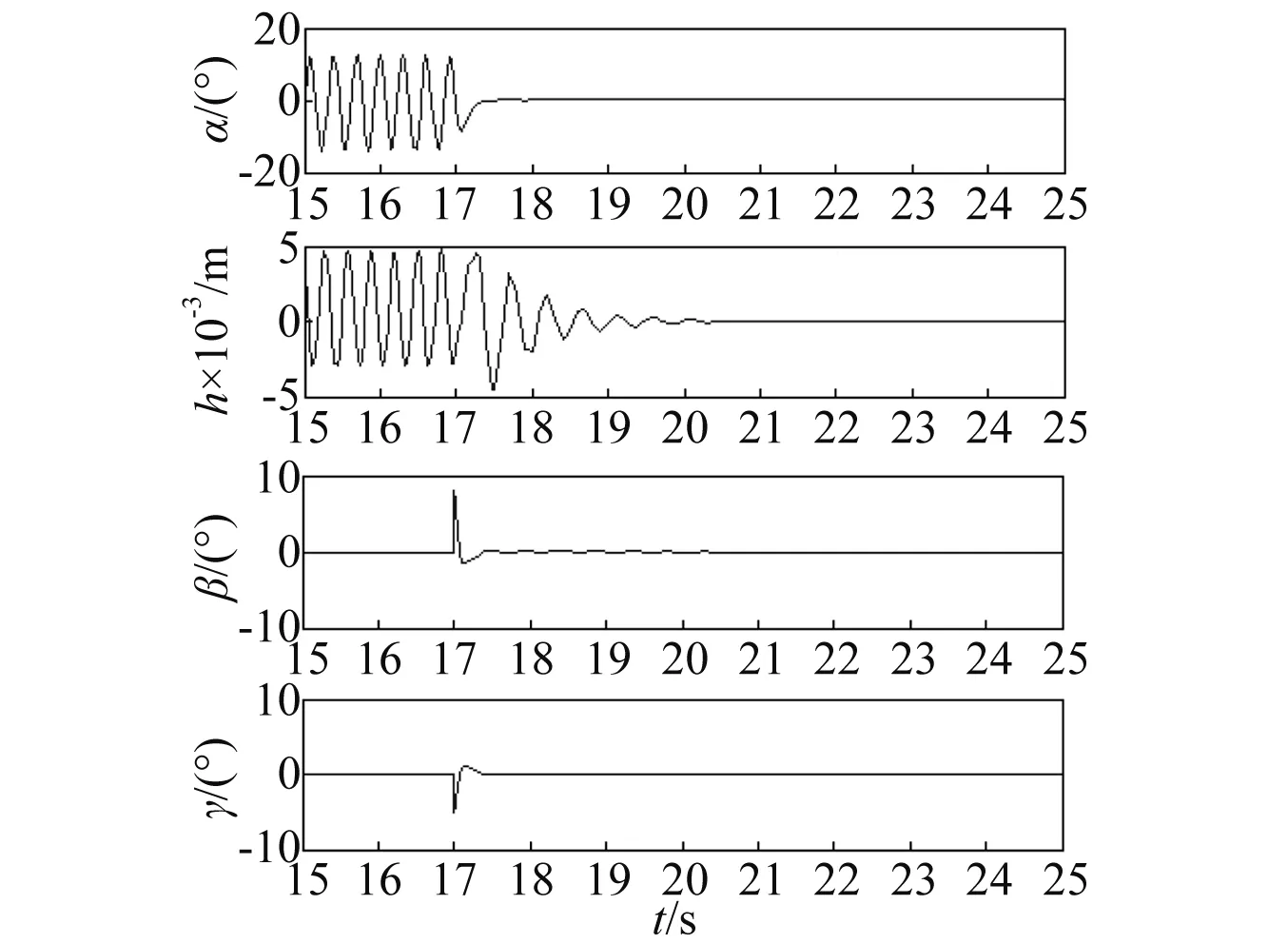
图6 SDRE非线性鲁棒控制 (Q=diag(10,100)，R=diag(10 000,500)，r=1 000)Fig.6 SDRE nonlinear robust control (Q=diag(10,100)，R=diag(10 000,500)，r=1 000)

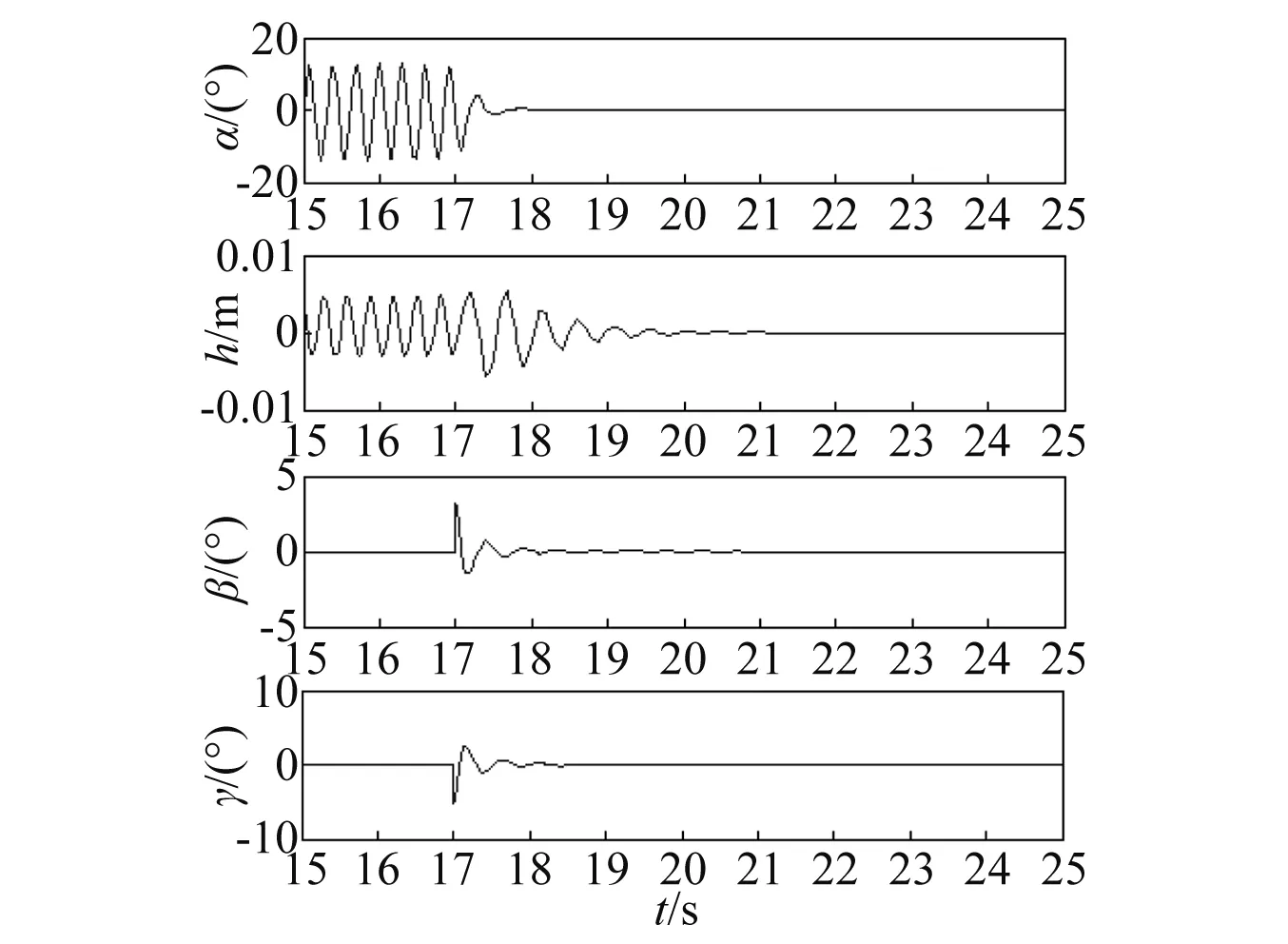
图7 SDRE非线性鲁棒控制 (Q=diag(1,10)，R=diag(10 000,200)，r=1 000)Fig.7 SDRE nonlinear robust control (Q=diag(1,10)，R=diag(10 000,200)，r=1 000)

由图5～7可得到各仿真结果的性能指标如表1所示。从表1可知，闭环系统在阵风干扰下都能快速到达稳态，且前/后缘控制面偏转角度都小于10°，说明该控制方法具有较好的控制效果，且控制效率较高；若权重矩阵Q变为原来的10倍时，系统状态量幅值变小，控制输入幅值变大，但未达到饱和状态；当权重矩阵R中r11/r22比值增大为原来的2.5倍时，控制输入β变小，γ变大。因此合理地选择权重矩阵Q和R，能优化系统响应和控制输入。

表1 性能指标对比

4 结 论

针对文献[5-6]所设计的SDRE非线性控制方法实质上并不能直接应用于二元机翼颤振的问题，设计了一种改进的SDRE非线性鲁棒控制方法。该方法通过对状态空间模型的等效变换，很好地解决了现有文献中SDRE非线性控制不能直接应用于二元机翼颤振的问题。仿真结果表明，在阵风干扰下，系统的沉浮位移、俯仰角和前/后缘舵偏角都能迅速地收敛于零；且前/后缘控制舵面偏转角度较小，都未达到系统的舵面偏转限制值，所设计的控制律具有较强的鲁棒性，实现了对二元机翼颤振现象的有效抑制。

[1] MUKHOPADHYAY V. Historical perspective on analysis and control of aeroelastic responses[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(5): 673-684.

[2] XIANG J W, YAN Y J, LI D C. Recent advance in nonlinear aeroelastic analysis and control of the aircraft[J]. Chinese Journal of Aeronautics, 2014, 27(1): 12-22.

[3] O’NEIL T, STRGANAC T W. Aeroelastic response of a rigid wing supported by nonlinear springs[J]. Journal of Aircraft, 1998, 35(4): 616-622.

[4] CASSARO M, BATTIPEDE M, MARZOCCA P, et al. Comparison of adaptive control architectures for flutter suppression[J].Journal of Guidance, Control, and Dynamics, 2015, 38(2): 346-354.

[5] SINGH S N, YIM W.State feedback control of an aeroelastic system with structural nonlinearity[J]. Aerospace Science and Technology, 2003, 7(1): 23-31.

[6] TADI M. State-dependent Riccati equation for control of aeroelastic flutter[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(6): 914-917.

[7] PLATANITIS G, STRGANAC T W. Suppression of control reversal using leading- and trailing-edge control surfaces[J]. Journal of Guidance, Control, and Dynamics, 2005, 28(3): 452-460.

[8] PLATANITIS G, STRGANAC T W. Control of a nonlinear wing section using leading- and trailing-edge surfaces[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(1): 52-58.

[9] LEE K W, SINGH S N. Control of a wing section using leading-and trailing-edge flaps by L1 adaptive feedback despite disturbances[C]∥51st AIAA Aerospace Sciences Meeting and Exhibit. Dallas, 2013.

[10] WANG Z, BEHAL A, MARZOCCA P. Model-free control design for multi-input multi-output aeroelastic system subject to external disturbance[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(2): 446-458.

[11] HAMMETT, K D. Control of nonlinear systems via the state feedback state-dependen Riccati equation techniques[D]. Edmond: Engineering of the Air Force Institute of Technology Air University , 1997.

[12] MORI T, DERESE A. A brief summary of the bounds on the solution of the algebraic matrix equations in control theory[J]. Iternationl Journal of Control, 1984, 39(2):247-256.

[13] RIDGELY D B, BANDA S S. Introduction to Robust Multivariable Control[D]. AFWAL-TR-85-3102, USAF, 1986.

Active flutter suppression for a two-dimensional airfoil based on an improved SDRE nonlinear robust control

GOU Yiyong, LI Hongbo, DONG Xinmin, YANG Rennong, ZUO Renwei

(Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi’an 710038, China)

In order to achieve the active flutter suppression of a two-dimensional airfoil, an improved state-dependent Riccati equation (SDRE) nonlinear robust control law was proposed based on the Lyapunov stability theory. The model of the two-dimensional airfoil with leading-and trailing-edge control surfaces was described in state space, and then the model was transformed into a form where the input matrixBis a full row rank matrix. The problem that the SDRE nonlinear control method can’t be directly applied to the active flutter suppression was solved. The simulation results were presented, which show the closed-loop system approaches to stability quickly under the impact of wind gust even if there is a hard constraint on the control input and the flutter suppression can be accomplished effectively. In addition, adjusting the weighting parametersQandRcan decrease the magnitude of control inputs.

two-dimensional airfoil; nonlinear robust control; flutter; state-dependent Riccati equation

国家自然科学基金(61473307；61304120)；航空科学基金(20155896026)

2016-01-13 修改稿收到日期：2016-01-15

苟义勇 男，硕士生，1991年11月生

董新民 男，博士，教授，1963年10月生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.10.024