基于自适应小波的二十辊轧机轧辊局部缺陷识别研究

吴胜利，邵毅敏，王利明，袁意林，叶维军

( 1. 重庆大学 机械传动国家重点实验室， 重庆 400030；2. 宁波宝新不锈钢有限公司, 宁波 315807 )

基于自适应小波的二十辊轧机轧辊局部缺陷识别研究

吴胜利1，邵毅敏1，王利明1，袁意林2，叶维军1

( 1. 重庆大学 机械传动国家重点实验室， 重庆 400030；2. 宁波宝新不锈钢有限公司, 宁波 315807 )

轧辊在磨削过程中，轧辊表面会产生振纹等局部缺陷，严重影响带钢表面质量，有效识别轧辊缺陷尺寸大小仍是目前轧机诊断存在的难题之一。利用MATLAB小波工具箱构造与信号对应的自适应小波，通过与Haar小波、Morlet小波和试验数据的对比分析，不仅证明了构建自适应小波方法的正确性，而且也验证了自适应小波对轧辊缺陷识别的有效性，为有效识别轧辊缺陷以及分析缺陷尺寸提供了理论基础和实践支撑。

轧辊缺陷；自适应小波；识别

轧辊表面存在缺陷时，在轧制过程中会在带钢表面产生相应的缺陷，不仅影响带钢表面质量，增加了停机更换轧辊的次数，而且严重影响企业生产效率和经济效益。因此建立有效识别的轧辊表面局部缺陷方法，可及时更换轧辊，减少不必要停机检查，提高产品质量与生产效率。

轧辊表面缺陷的形态、初始剥落断口的材料特性有较为广泛的研究[1-2]，尤其是工作辊直接与带钢表面接触，粗糙度对带钢表面质量影响等[3]。当轧制过程中工作辊表面产生剥落等缺陷时，有效提取其振动特征及时更换轧辊是减少经济损失的主要手段[4]。自适应选取最匹配尺度系数特征小波，同时利用遗传算法进行参数的优化，可有效地提高信号的信噪比[5-6]。改进阈值量化公式方法和遗传算法小波基搜索方法，构建的自适应小波能在强噪声环境下有效提取微弱的故障冲击信号和识别早期故障特征频率[7-8]。有研究表明小波的形状越逼近冲击信号，越有利于故障特征的提取[9]。

目前的研究，主要集中在轧辊表面缺陷缺陷对带钢表面质量的影响和自适应小波构建的方法方面。但是，如何利用自适应小波提取轧辊表面缺陷，特别是对缺陷尺寸识别方面的研究较少。因此，基于自适应小波，通过与Haar小波及试验数据的对比分析，提出了自适应小波的二十辊轧机轧辊局部缺陷识别方法，为实现轧辊表面缺陷尺寸的识别提供了一条新的途径。

1 自适应小波的构造

构造与原始信号相似的自适应小波，必须保证截取的信号至少应该是一个完整的周期，否则将影响分析结果准确性。在希尔伯特空间对截取信号与原始信号进行了相似性判断与衡量，两信号最小能量误差Emin可表示为[10]

Emin=‖x‖2-(x,y)/‖y‖2

(1)

式中，x为原始信号，y表示截取的信号并进行延拓。同时式(1)可以表示为

(2)

式中，Rxy=(x,y)/‖x‖‖y‖。Rxy越大能量误差越小，即表示两信号相似程度越高。信号相似性判断及自适应小波分析流程图，如图1所示。

图1 自适应小波分析流程Fig. 1 Analysis algorithm of adaptive wavelet

构造小波函数ψ(t)必须满足小波函数的基本条件[11]：

(1) 小波函数值在很小区间之外等于0；

(2) 小波函数的均值应该为0，即

(3)

(3)满足小波函数的容许条件，即

(4)

利用MATLAB小波工具箱，构造与信号形状类似或者逼近的小波，与仿真信号对应的小波，如图2所示。

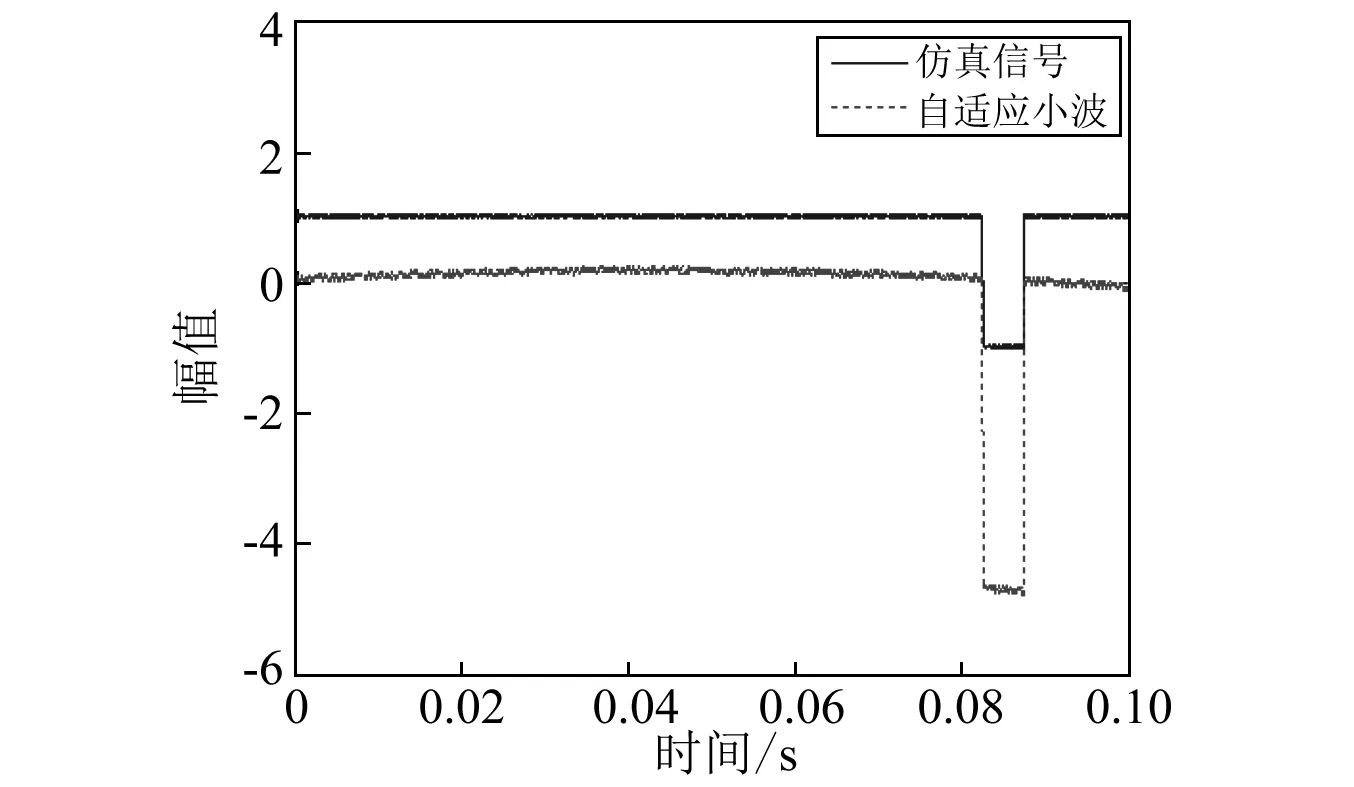
图2 仿真信号及对应的自适应小波Fig.2 Simulated signal and the corresponding adaptive wavelet

2 自适应小波与Haar小波对比分析

加入随机噪声的周期冲击仿真信号，如图3所示。根据Jena的研究，在现有的小波中，Haar小波在形状上与仿真信号比较接近，因此选择Haar小波对仿真信号进行时频分析，如图4(a)所示，自适应小波对仿真信号的分析结果如图4(b)所示。

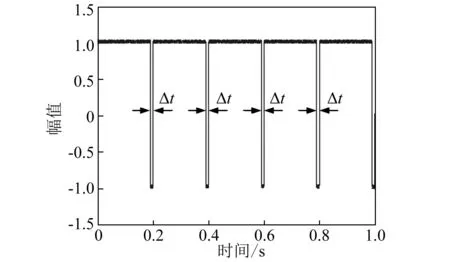
图3 仿真信号Fig.3 Simulated signal

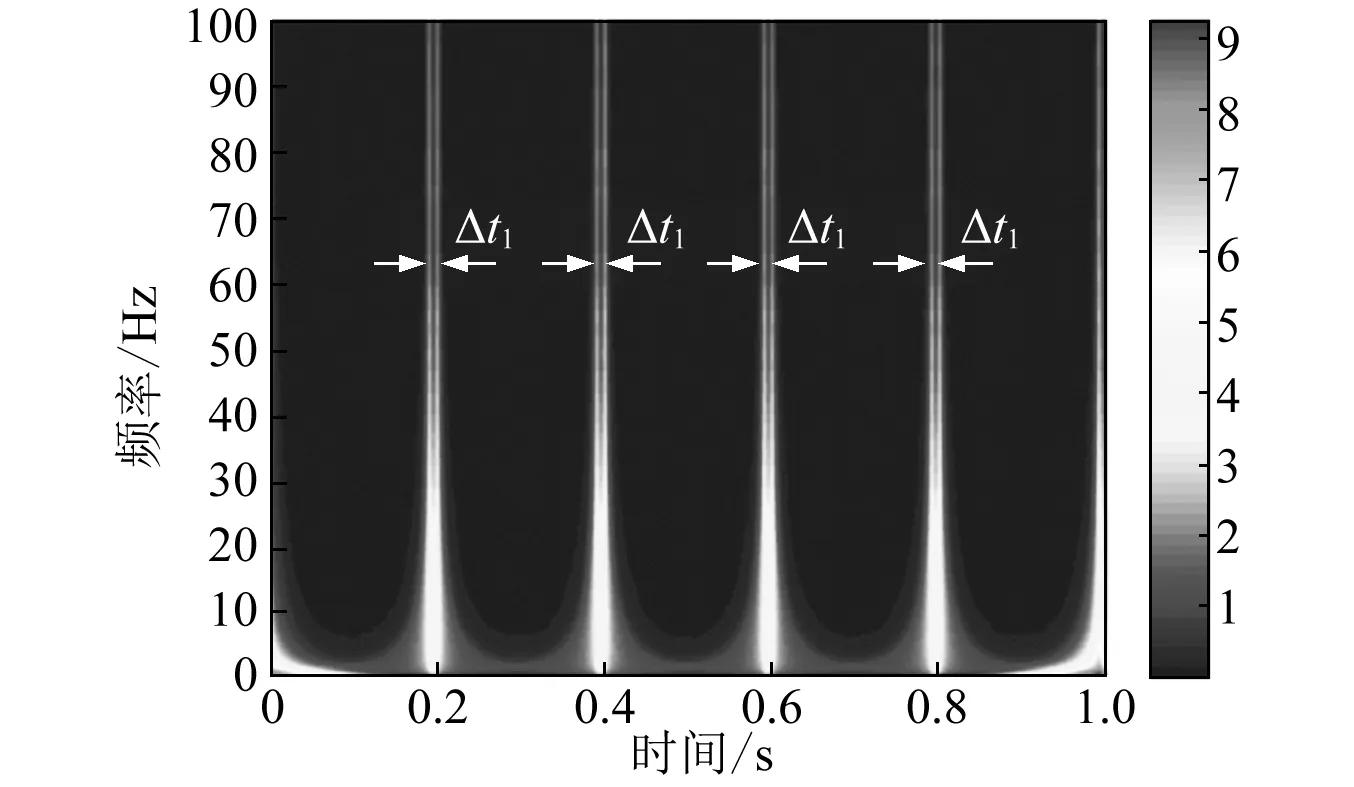
(a)Haar小波分析结果

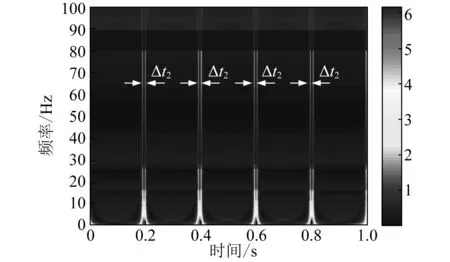
(b)自适应小波分析结果图4 不同小波对仿真信号分析结果Fig. 4 Results of simulated signal based on different wavelets

通过对比分析可以得到，Δt=Δt1=Δt2，构造的自适应小波与Haar取得了相同的效果，并且冲击的间隔与仿真信号时域间隔相同。因此构造与冲击信号相对应的小波，就能有效的识别冲击持续时间，即缺陷尺寸的大小。

3 二十辊轧机试验验证

轧辊表面存在的缺陷及对应的带钢表面，如图5所示，轧辊上的缺陷将在反映在带钢表面。利用B&K加速度传感器和放大器，LMS数据采集装置进行数据采集，采样频率为20 480 Hz，如图6所示。轧机支撑辊直径D7=D8=D9=D10=300 mm，第二中间辊直径D4=D5=D6=173 mm，第一中间辊直径D2=D3=98.4 mm，工作辊直径D1=67.2 mm。测试时轧机主要轧制参数，如表1所示。

表1 测试时轧机主要轧制参数

图5 轧辊表面缺陷及相应的带钢表面Fig. 5 Defects on the surface of roll and the corresponding surface of steel strip

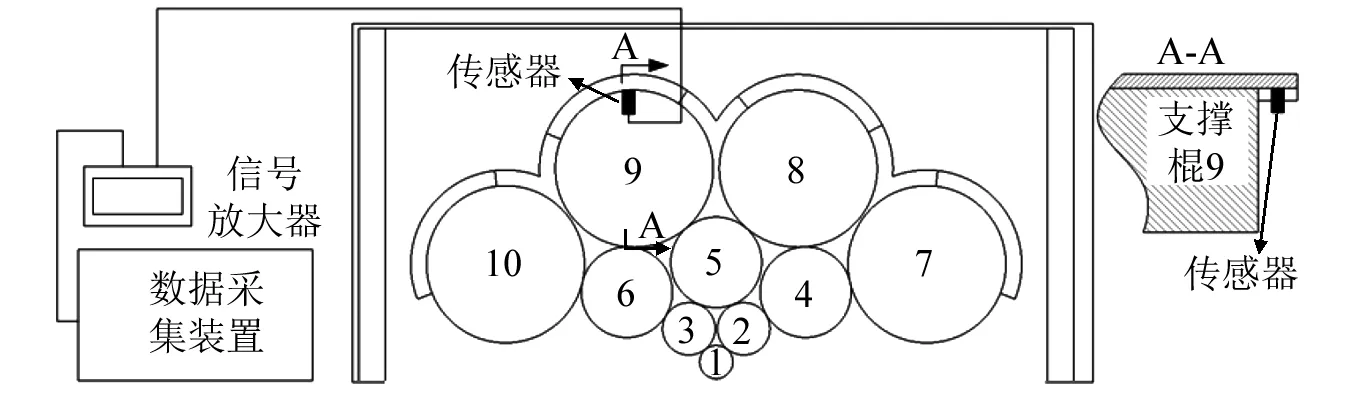
图6 传感器布置及数据采集系统Fig. 6 Location of sensor and the data acquisition device

轧辊存在缺陷时的测试信号，如图7所示。可以得到信号中存在明显的周期性冲击，并构造与其相对应的小波。Morlet小波与测试信号形状比较接近，因此采用Morlet小波与构造的小波对测试信号进行对比分析，Molet小波时频分析结果，如图8(a)所示，利用构造的自适应小波分析结果，如图8(b)所示。

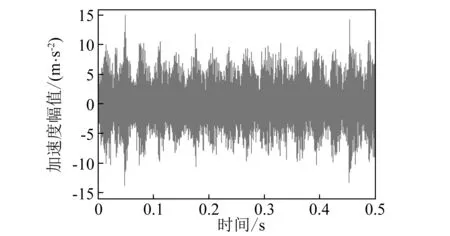
图7 试验测试信号Fig. 7 The experimental signal

(a)Morlet小波分析结果

(b)自适应小波分析结果图8 不同小波对试验信号分析结果Fig. 8 Results of measured signal based on different wavelets

Morlet小波与测试信号形状接近，但分析结果只看到带钢表面振纹的频率，不能有效地识别缺陷的存在；利用构造的小波对测的信号的分析可以得到，图中画出的虚线间隔与振纹宽度一致，不仅有效地识别了振纹的频率，同时冲击的间隔基本等于缺陷沿轧辊圆周方向的宽度。不仅验证了构造小波的有效性，同时也为实时准确识别轧辊表面缺陷，提供了理论与实践方法。

4 不同宽度冲击特性分析

图9(a)，(b)，(c)所示的分别为冲击宽度为10%，15%，20%时的仿真信号；用构造的自适应小波进行分析，如图10所示。图10(a)，(b)，(c)所示的分别为冲击宽度为10%，15%，20%时的分析结果，可以得到，分析结果宽度与原信号冲击间隔相同，并随着冲击间隔的增大，分析结果的宽度也随之增大。

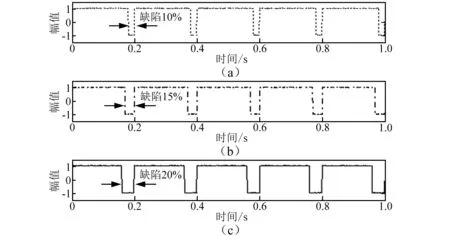
图9 不同宽度冲击的仿真信号Fig. 9 Simulated signals with different sizes defects

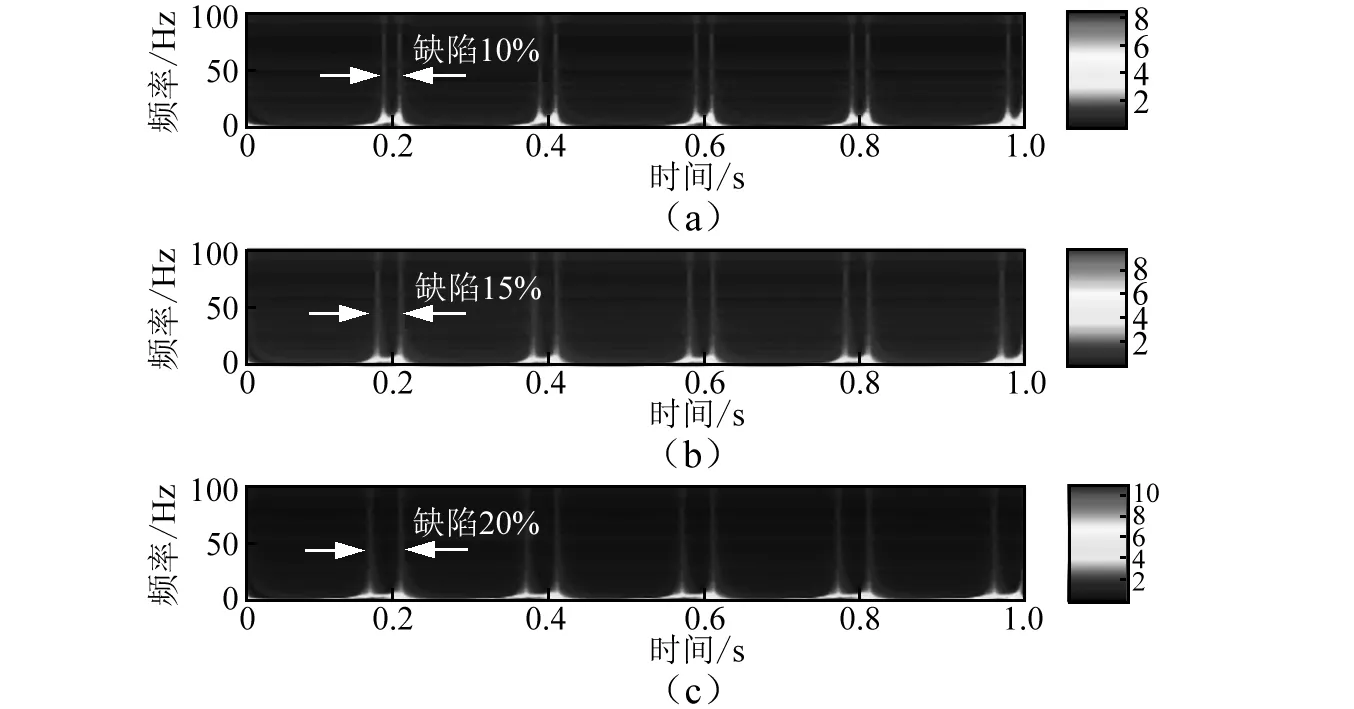
图10 不同宽度冲击时利用对应自适应小波分析结果Fig. 10 Results of simulated signals with different sizes defects based on the adaptive wavelets

5 结 论

本文提出了自适应小波的二十辊轧机轧辊局部缺陷识别方法，可对冲击的宽度进行有效识别，经与含有表面缺陷的轧辊现场轧制试验结果对比，验证了构建的自适应小波不仅准确提取故障特征频率，而且对缺陷尺寸大小进行有效的识别，该方法为准确定位剥落、凹坑等缺陷尺寸大小提供了提供了新的手段。

[1] LI H, JIANG Z, TIEU K A, et al. Analysis of premature failure of work rolls in a cold strip plant[J].Wear, 2007,263(7):1442-1446

[2] WU Qiong, SUN Dale, LIU Changsheng, et al. Analysis of surface and sub-surface initiated spalling of forged cold work rolls[J]. Engineering Failure Analysis, 2008,15(4):401-410.

[3] 魏立新，高江曼，麻诚,等. 冷轧平整机工作辊表面粗糙度衰减模型[J]. 钢铁，2015，50(6): 51-56. WEI Lixin，GAO Jiangman，MA Cheng, et al. Attenuation model for working roll’s surface roughness in cold rolling temper

mill[J]. Iron and Steel，2015, 50(6):51-56.

[4] WU S, WANG L, SHAO Y, et al. Vibration characteristic analysis of twenty-high rolling mill with local defect on roll surface based on the time-varying contact stiffness[J]. Engineering Failure Analysis, 2014, 42(5): 297-310.

[5] 阳子婧, 蔡力钢, 高立新. 自适应冗余提升小波降噪分析及轴承故障识别应用[J]. 振动与冲击, 2013,32(7):54-57. YANG Zijing, CAI Ligang, GAO Lixin. Adaptive redundant lifting wavelet denoising analysis and its application in bearing fault identification [J]. Journal of Vibration and Shock, 2013,32(7):54-57.

[6] CHEN H X, CHUN P S K, LIM G H. Adaptive wavelet transform for vibration signal modeling and application in fault diagnosis of water hydraulic motor [J]. Mechanical Systems and Signal Process, 2006,20(8):2022-2045.

[7] 刘文艺, 汤宝平, 蒋永华. 一种自适应小波降噪方法[J]. 振动、测试与诊断, 2011,31(1):74-77. LIU Wenyi, TANG Baoping, JIANG Yonghua. Research on an adaptive wavelet denoising method [J]. Journal of Vibration, Measurement & Diagnosis, 2011,31(1):74-77.

[8] BELSAK A, FLASKER J. Determining cracks in gears using adaptive wavelet transform approach [J]. Engineering Failure Analysis, 2010,17(3):664-671.

[9] JENA D P, PANIGRAHI S N. Bearing and gear fault diagnosis using adaptive wavelet transform of vibration signals [J]. Procedia Engineering, 2012,50:265-274.

[10] 辛玉忠, 刘常凯. 判断与衡量两个信号相似性的内积表达式[J]. 潍坊学院学报, 2002, 2(4): 11-12. XIN Yuzhong, LIU Changkai. Inherenet product posture about judging two signals resemble quality[J]. Journal of Weifang University, 2002, 2(4): 11-12.

[11] 褚福磊，彭志科，冯志鹏，等. 机械故障诊断的现代信号处理方法[M]. 北京：科学出版社, 2009:34-36.

Identification of local defects on the roll surface of a twenty-high roll mill based on the adaptive wavelet

WU Shengli1, SHAO Yimin1, WANG Liming1, YUAN Yilin2,YE Weijun1

(1.State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400030, China; 2. Ningbo Baoxin Stainless Steel Co.,Ltd., Ningbo 315807, China)

Local defects are prone to appear on the surface of roll in grinding process, which seriously affect the quality of the steel strip. The identification of defects and the sizes of defects are still existing difficult problems. The MATLAB wavelet toolbox was used to generate an adaptive wavelet. The a greement between the results of the adaptive wavelet and the Haar, Morlet wavelet and the experimental results validates the effectiveness of the generated adaptive wavelet method. The results also provide a theoretical support for identifying defects on the surface of roll.

local defect on the roll; adaptive wavelet; identifying

国家自然基金重点资助项目(51035008)

2015-06-13 修改稿收到日期： 2016-07-13

吴胜利 男，博士生，1983年生

邵毅敏 男，教授，博士生导师，1963年生

E-mail: ymshao@cqu.edu.cn

TH165.3

A

10.13465/j.cnki.jvs.2017.10.019