热声载荷下C/SiC层合薄板动态响应分析及寿命预测

白文君，沙云东，李华山，唐晓宁

(沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室，沈阳 110136)

热声载荷下C/SiC层合薄板动态响应分析及寿命预测

白文君，沙云东，李华山，唐晓宁

(沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室，沈阳 110136)

鉴于处在热声载荷下的薄壁结构工作条件恶劣，极易发生屈曲和声疲劳从而影响构件的稳定性和使用寿命。以四边固支C/SiC复合材料层合板结构为研究对象，运用有限元方法计算结构在不同温度和声压级组合下的振动响应，分析屈曲前后响应特性并总结了典型的非线性振动响应特性；基于复合材料层合板高比强和特殊的结构疲劳损伤机理特点，运用改进的雨流法统计了层合板在超高温度强噪声工况下的应力响应，结合材料对称循环疲劳性能试验所得数据拟合地考虑平均应力影响的等效寿命公式和Palmgren-Miner线性累积损伤准则估算层合板的疲劳寿命。

C/SiC层合板；热声载荷；应力动态响应；雨流法；疲劳寿命

研究表明[1]：复杂的载荷使航天器热防护系统(TPS)局部表面温度达3 000 °F，局部系统的噪声声压级甚至可达180 dB。在国外航天飞行器上复合材料所占比例越来越多，最典型当属应用在“幻影”2000战斗机和“狂风”战斗机的M88航空发动机上[2-3]。还有应用于液体火箭发动机喷管扩张段，壁厚仅1.5 mm可承受高温下1 200 MPa的应力负载[4]。在实际应用中，复合材料薄壁结构在高温强噪声作用下表现大挠度非线性响应，这就使疲劳寿命预测变得极度困难[5-7]。但由于高成本以及在高声强和高温试验仪器方面存在的诸多困难都使获取可靠的试验数据变得异常困难，这就促使研究提高数值和模拟预测的能力。Dafedar等[8-9]通过高阶剪切变形理论分析了复合材料层合板的热后屈曲响应，由于在推导应力-位移关系时忽略非线性应变项限制其只能应用于较小的初始后屈曲区域。而通过引入模态交互或使用有限元方法则可大大提高结果的准确性并扩大在后屈曲区域的应用范围。Ibrahim等[10]采用一种有限单元法对热载荷与随机声载荷联合作用下的复合材料板结构非线性随机响应进行研究；国内对于热声激励响应及疲劳地研究起步较晚，钟轶峰等[11]采用变分渐近法、渐近修正几何非线性理论和广义Galerkin方法计算了复合材料层合板在面内不可移边界下的热后屈曲解析解，构建相对简单、便于实际应用的层合板热后屈曲响应和模态跃迁分析方法，为解决复合材料层合板各向异性和非线性带来结构复杂性等问题提供理论参考；杨雄伟等[12]利用混合有限元-统计能量分析(FE-SEA)法对整体复杂结构在宽频内的声振特性进行数值分析；Sha等[13-14]对热声载荷作用下高温合金薄壁结构非线性响应地长期持续研究，在载荷模型、加载方式、响应计算和疲劳分析等方面取得了一定进展，并形成了系统的分析方法。鉴于目前大多采用的宏观唯象定义方法所确定的疲劳累积损伤，如剩余刚度模型、剩余强度模型、耗散能模型和关键单元模型等并不能完全刻画出复合材料层合板真实工况下的疲劳过程，因此将基于Palmgren-Miner线性累积准则并结合雨流循环计数法的寿命估算方法应用于复合材料层合板疲劳寿命预测中在理论上具有可行性。

本文研究了热声载荷作用下的C/SiC复合材料层合薄板动态响应和疲劳寿命，运用有限元法计算出热声联合载荷作用下该薄板结构的动态响应，通过改进的雨流循环计数法对应力循环计数，并采用Morrow平均应力模型获取了零平均应力地等效循环。由于复合材料层合板疲劳损伤不同于金属结构中拉应力主导下地大裂纹扩展断裂损伤，此处采用Von Mises应力计算，随后结合疲劳寿命曲线及Miner线性累积损伤准则估算该结构疲劳寿命。

1 热声载荷作用下的复合材料层合板结构控制方程

由经典板壳理论的Kirchhoff假设和Karman-type 几何非线性推导出总应变为：

{ε}={ε0}+z{k}

(1)

式中：{ε0}表示中面应变向量，{k}表示中面曲率向量；令u，v分别表示层合板中面沿x轴和y轴方向的位移，ω表示中面的横向位移，且{ε0}和{k}可分别如下

(2)

(3)

对于承受温度梯度ΔT(x,y,z)载荷的k层铺设横观各向同性复合材料层合薄板，其应力-应变本构关系如下式所示：

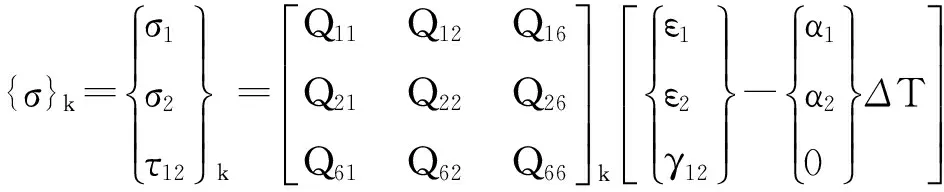
(4)

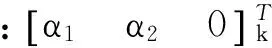
(5)

(6)

(7)

式中c=cos(φ)，s=sin(φ)。统一式(4)、(5)、(6)、(7)对于承受温度载荷ΔT(x,y,z)的k层铺角为φ的复合材料，其本构关系可以表示为：

(8)

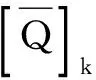
(9)

综合中面应变后得复合材料层合板本构关系为：

(10)

其中[A]、[B]、[D]分别为层合板拉压刚度矩阵(只与面内内力和中面应变有关)、拉弯耦合刚度矩阵(只与拉伸和弯曲有关)和弯曲刚度矩阵(只与内力矩和曲率及扭曲率有关)，且：

(11)

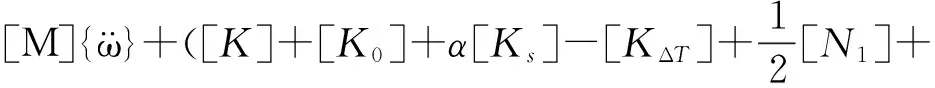
(12)

[M]代表质量矩阵；[K]代表线性刚度矩阵，[K0]和[Ks]代表恢复力刚度矩阵，[KΔT]代表由所施加热载荷引起的层合板内部热应力刚度矩阵；[N1]和[N2]分别表示一阶、二阶非线性刚度矩阵；{pp(t)}、{pΔT}和{pr}则分别表示声载荷矢量、热载荷矢量和恢复力矢量。求解该方程方法很多，一般将响应分为静态响应和动态响应分别求解，利用Newton-Raphson迭代法先确定静态响应，随后运用泰勒级数展开求解动态响应，也可以用联合标准模态法和等效线性化方法确定动态响应，至此便求出整个响应，回代入上述诸公式便可求得应变和应力。

2 数值分析与讨论

2.1 计算模型

本文选取单层厚0.2 mm的铺角为[90°/45°/0°/-45°/-90°/-90°/-45°/0°/45°/90°]s对称铺设四边固支C/SiC层合矩形薄板作为研究对象，几何体为600 mm×400 mm×4 mm如图1所示。分别选取表1所示纤维和基体材料参数并应用代表体积元计算可得材料属性。声载荷处理为(SPL) 声压级幅值服从高斯分布的均匀白噪声，带宽为0～1 500 Hz，覆盖前八阶结构模态，噪声信号时长为1.2 s，其功率谱密度为：

(13)

设环境温度为Tref，临界屈曲温度为Tcr，薄板的温度为T，则可用屈曲系数S来表示板受热所处的状态，令S=(T-Tref)/Tcr当S<1、S=1、S>1 时，薄板分别处于热屈曲前状态、热屈曲状态及热后屈曲状态。

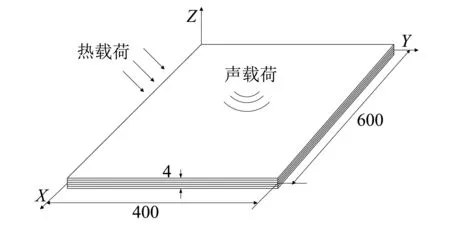
图1 热声载荷作用下的四边固支层合板示意 图(mm)Fig 1. Schematic of clamped supported laminated plates under thermal acoustic loadings (mm)

材料E1/GPaE2/GPaG12/GPaG23/GPaρ/kg·m3)μ12μ23T300(纤维)22013.894.817500.20.25Sic(基体)30030012512532000.20.2

对复合材料层合板结构进行模态分析得其前八阶固有频率，如表2所示。分别将150 dB，160 dB，170 dB的随机声载荷以面力的形式均匀地施加在模型的所有单元上，热载荷以面力均匀施加在模型的所有节点上，为防止载荷冲击的影响，截取0.2～1.2 s热声响应特性分析如下。

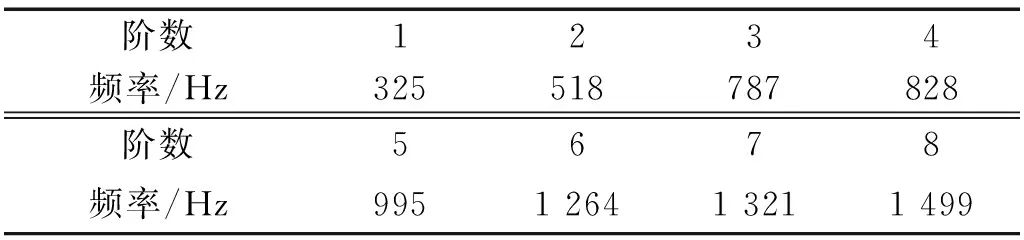
表2 C/SiC层合板前八阶固有频率

2.2 恒温下层合板的横向位移响应

图2～4所示为同温(S=1.35)不同声压级下层合板中点横向位移时间历程。当声压级从150 dB逐步升至170 dB时横向运动从一个平衡位置振动逐渐变为沿两个平衡位置之间的间歇跳变运动并最终变为持续跳变运动。跳变运动就是当薄板处于屈曲后区域(此时S>1)，结构有两个势能最低点，对应着两个屈曲后平衡位置，初始平衡位置变为不稳定平衡位置，当受到较小激励时，结构将在任一势能井中围绕屈曲后平衡位置做小幅振动；如果受到较大激励，结构将在两个势能井间跳跃，在两个屈曲后平衡位置间做跳变运动。170 dB下横向位移明显比150 dB下横向位移大，这是因为相同温度下，声压级大意味着总激励能量大，随着声强逐渐增大，响应非线性趋势也逐渐增强。在这一过程中，层合板中点围绕初始平衡位置的小幅值随机振动在外界大能量激励作用下其振动幅值会逐渐增大，达到一定程度后开始从围绕一个平衡位置随机振动转变为围绕两个平衡位置间歇跳变运动，而持续增大外界激励致使薄板由间歇跳变运动转变为围绕两个平衡位置地连续跳变运动。

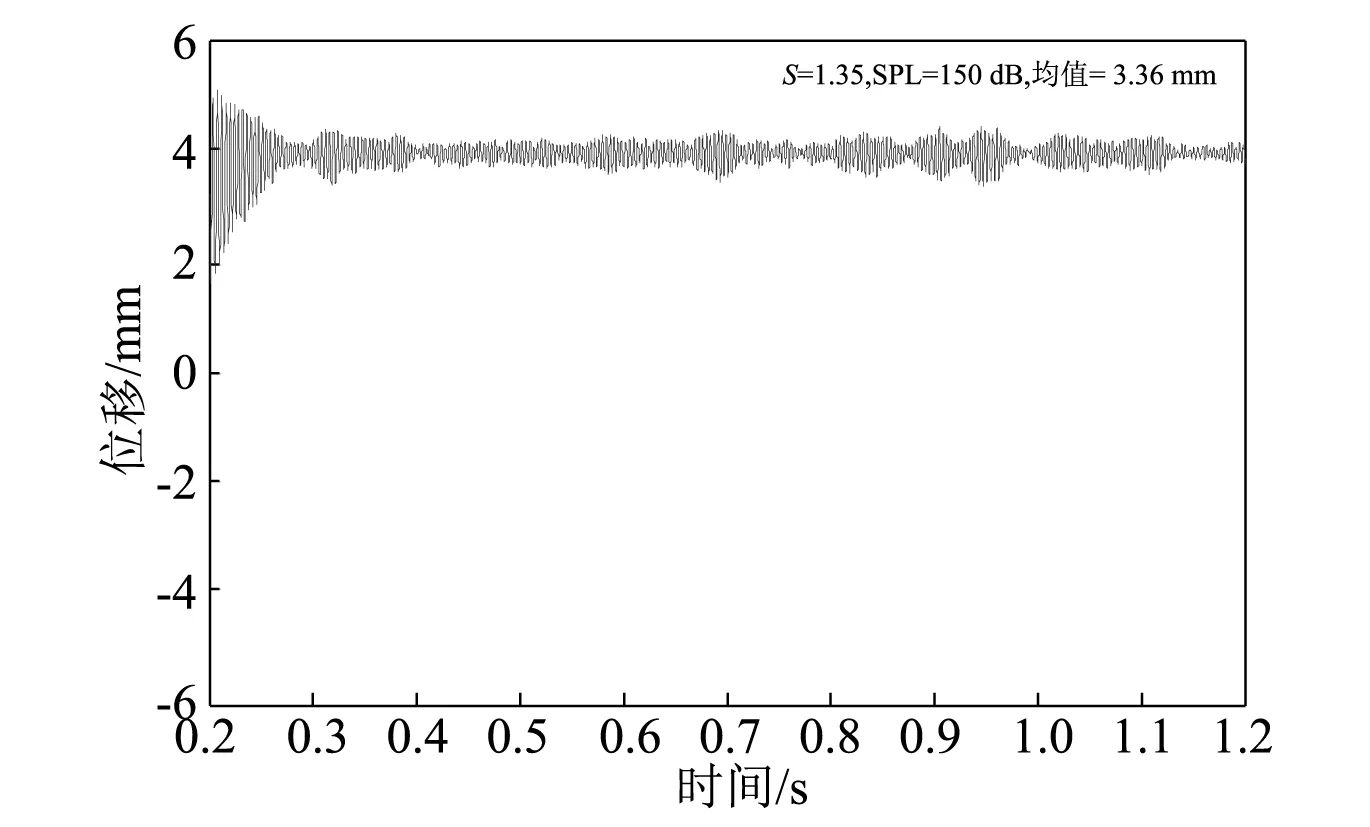
图2 S=1.35 SPL=150 dB位移时间历程Fig 2. Displacement time history at S=1.35,SPL=150 dB

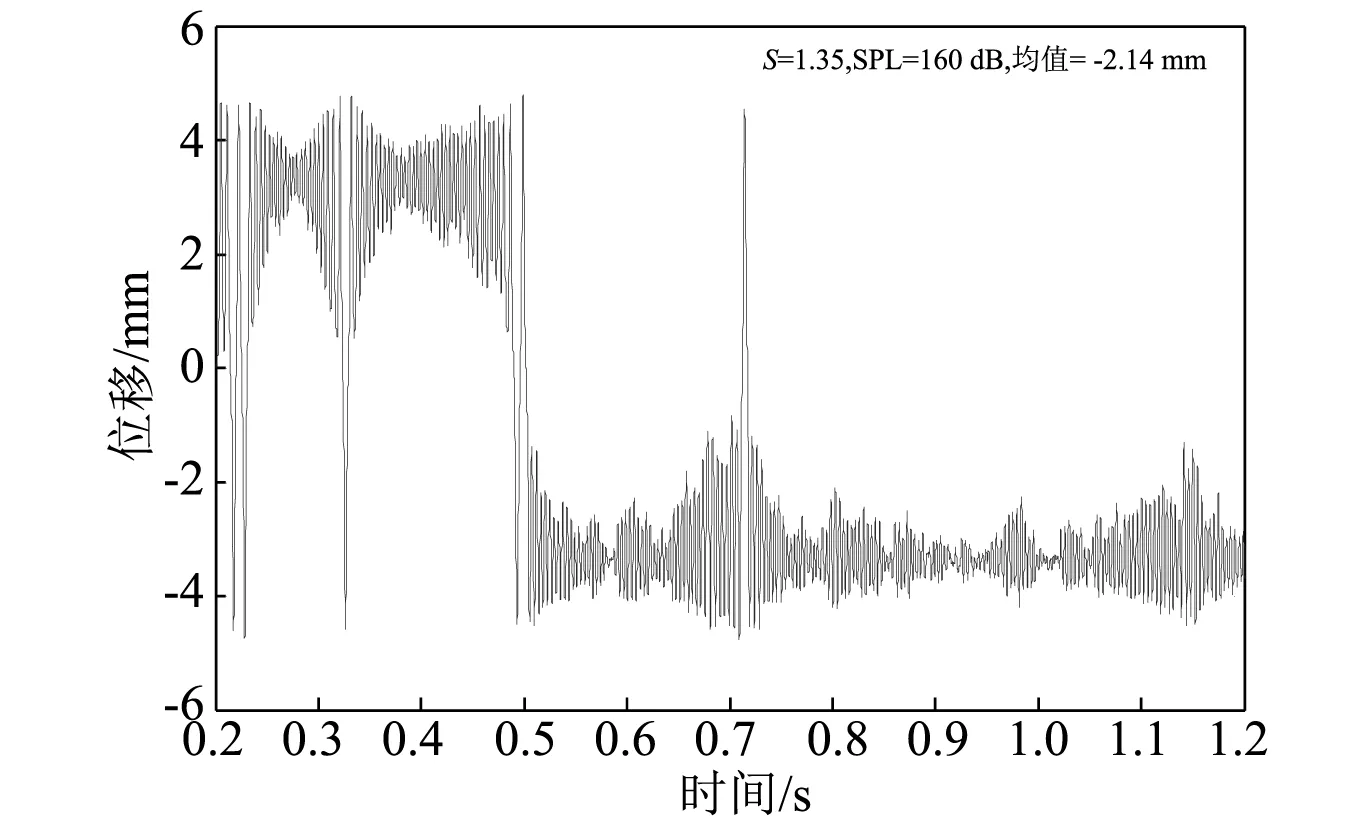
图3 S=1.35 SPL=160 dB位移时间历程Fig 3. Displacement time history at S=1.35,SPL=160 dB

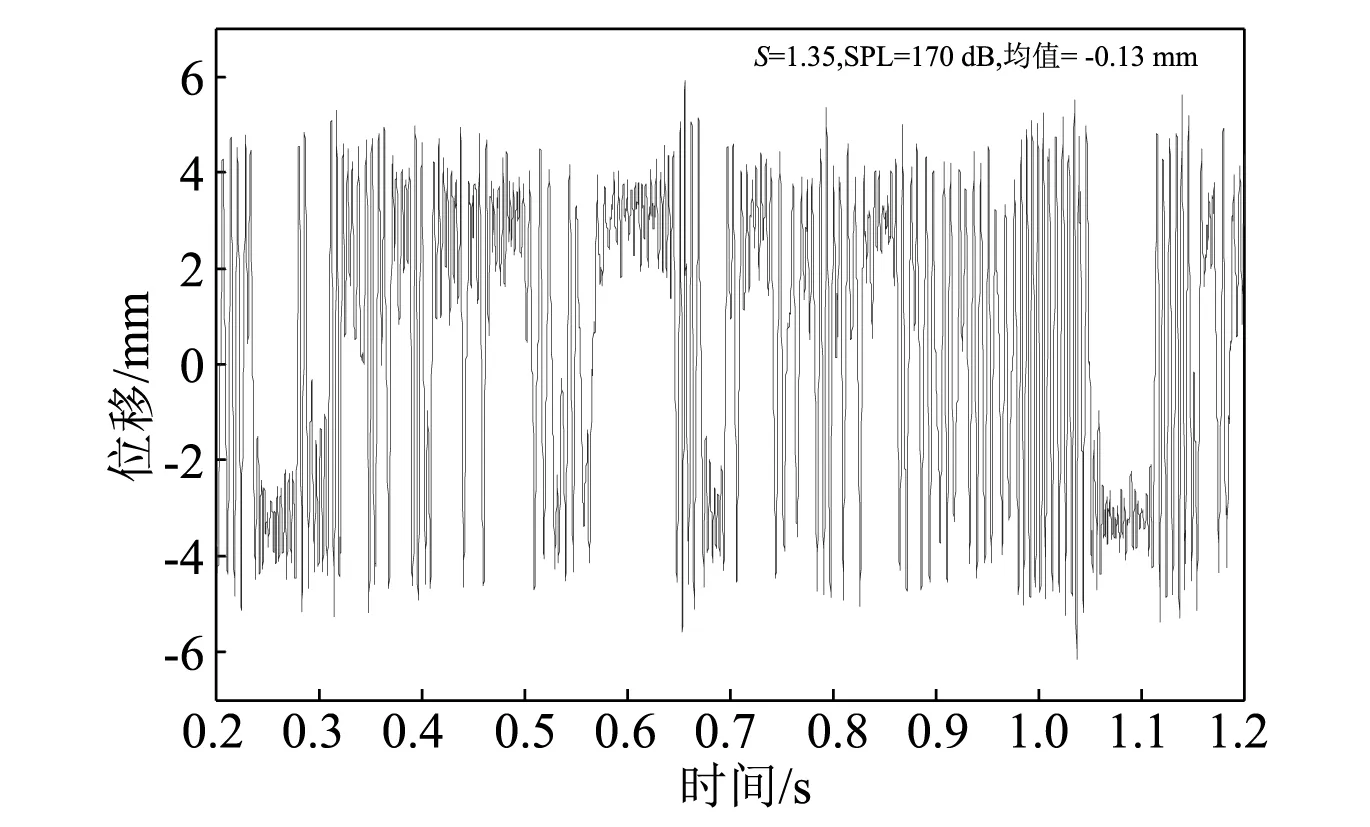
图4 S=1.35 SPL=170 dB位移时间历程Fig 4. Displacement time history at S=1.35,SPL=170 dB

2.3 恒定声压级下层合板的横向位移响应

结合图3以及图5～8所示相同声压级(SPL=160 dB)不同温度下的层合板中点横向位移响应。从图中可以观察出随着温度逐渐趋近于临界屈曲温度，相同声载荷激励下的振动幅值增大；温度处于室温时，层合板围绕初始平衡位置作随机振动；随着温度增加至临界屈曲温度，层合板在临界屈曲时的位移响应明显大于室温时的响应；当温度持续增加至高于临界屈曲温度时，层合板由围绕初始平衡位置地随机振动转变为围绕屈曲后平衡位置之间地跳变运动，随后表现为只围绕屈曲后某一平衡位置随机振动的运动趋势。这是由于屈曲系数增大，势能井加深，跳变运动会逐渐减少，直至被限制在单一势能井中，此时即表现为层合板围绕屈曲后某一平衡位置振动；若温度继续增大直至屈曲系数远大于层合板临界屈曲系数，此时可认为层合板处于超高温环境下围绕屈曲后某一平衡位置作低幅值振动而没有发生跳变响应，这也验证了上述趋势预测的正确性。

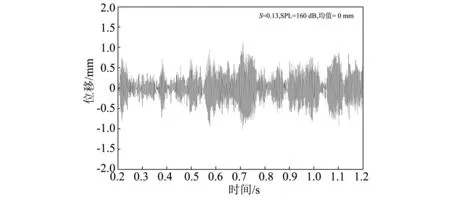
图5 S=0.13 SPL=160 dB位移时间历程Fig 5. Displacement time history at S=0.13,SPL=160 dB

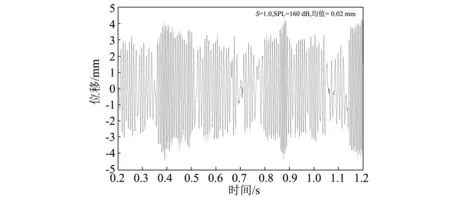
图6 S=1.0 SPL=160 dB位移时间历程Fig 6. Displacement time history at S=1.0,SPL=160 dB

图7 S=1.2 SPL=160 dB位移时间历程Fig 7. Displacement time history at S=1.2,SPL=160 dB

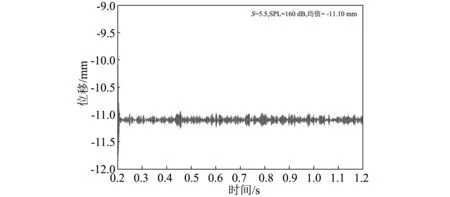
图8 S=5.5 SPL=160 dB位移时间历程Fig 8. Displacement time history at S=5.5,SPL=160 dB

从能量方面考虑，当层合板进入热后屈曲状态，随着温度载荷地增加，跳变响应只有在更高声压级地噪声载荷激励下才会发生。当温度载荷增加到某一特定高温载荷值后，实际工程中的噪声载荷声压级达不到跳变响应所需值，此时层合板就会围绕屈曲后某平衡位置做小幅值振动而不会再发生跳变响应；从结构自身固有特性方面考虑，这是因为处于超高温条件下，复合材料层合板内不同相界面处的张力作用增大了板的面外刚度，板内薄膜力沿厚度方向分布不均匀所产生的附加弯矩致使其发生硬化现象出现了永久屈曲变形，因而屈曲后在超高温强声载荷激励下层合板振动幅值相对于屈曲温度附近层合板振动幅值反而减小。

2.4 恒温下层合板应力响应PSD

图9～11表明恒温下声压级变化对四边固支层合板等效应力功率谱密度的影响，分别揭示了屈曲前、屈曲时和屈曲后结构应力响应随声压级的变化。由图9可知，层合板处于屈曲前，响应呈现弱非线性，随着声压级增大，基频增大不明显，对应于声压级分别为150 dB、160 dB和170 dB下的基频分别为303 Hz、308 Hz以及310 Hz；从图10可知，在临界屈曲温度下，响应完全为非线性响应，对应声压级为150 dB、160 dB、170 dB时的基频分别为90 Hz、105 Hz以及151 Hz，即随着声强增加，基频增加量明显，说明此时非线性响应已经完全占主导地位；图11为屈曲后结构应力响应随声压级的变化情况，150 dB时基频为256 Hz，160 dB时基频为252 Hz，170 dB时基频为166 Hz，屈曲后温度不变随声载荷增大基频下降。

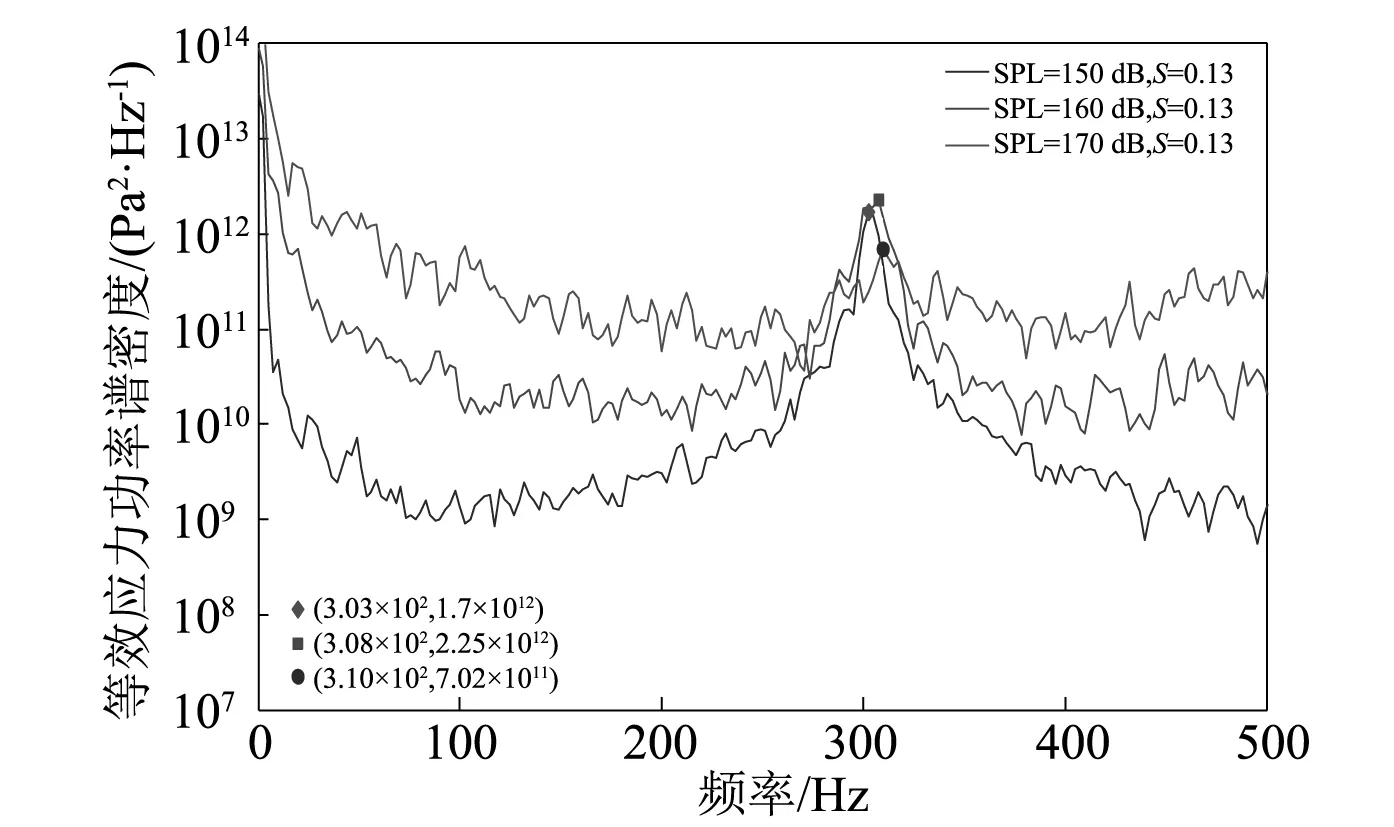
图9 S=0.13不同声压级下应力功率谱密度Fig 9. Stress PSDs at S=0.13 and varied SPLs

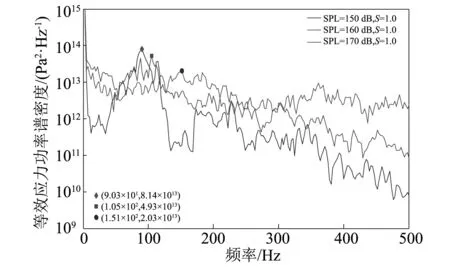
图10 S=1.0不同声压级下应力功率谱密度Fig 10. Stress PSDs at S=1.0 and varied SPLs

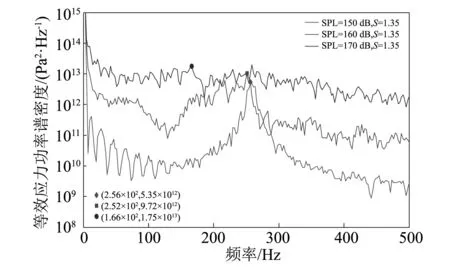
图11 S=1.35不同声压级下应力功率谱密度Fig 11. Stress PSDs at S=1.35 and varied SPLs

声载荷对结构作用实则是结构表面承受一种有一定频率分布特性且呈现空间分布的动态随机压力载荷。当所施加噪声载荷的频率分布特性与结构自身动态特性相互耦合时，结构就会发生明显的应力响应。若结构长时间频繁承受这种耦合作用，就会在应力集中或其他缺陷部位产生疲劳裂纹，并最终导致疲劳破坏。层合板由屈曲前逐渐向屈曲后转变时，随声压级增大，层合板的响应也由最初的弱非线性逐渐转变为非线性响应，同时应力幅值总体上呈现出先增大后减小的趋势且减小速率小于增大速率。在这一过程中，还伴有结构软化和硬化现象的出现，而这又与结构疲劳过程中累计损伤有较为紧密的联系。层合板受硬化作用的影响而得以强化其内部，此时的疲劳过程中并行存在着强化和损伤，这两个过程相互叠加致使结构损伤过程得到抑制而变缓慢，此时累计损伤就会大于1，软化过程则与之相反。

2.5 恒定声压级下层合板应力响应PSD

图12～13表征结构受恒定声压级作用下温度呈递增变化对等效应力功率谱密度的影响。热屈曲前随着温度逐渐升高，层合板基频由S=0.13时的308 Hz降低至S=1.0时的105 Hz，此时层合板共振基频下降到最小。热屈曲就是在热载荷作用下的薄壁结构四边受到约束后不能自由膨胀，结构构形从原来的平衡状态突然跳转到另一种随遇的平衡状态。在热屈曲前，随温度升高材料弹性模量变化，结构伴随着软化过程，刚度减弱，导致结构基频减小；在热屈曲后阶段，温度逐步升高致使结构逐渐硬化，刚度增强导致其基频增大；以至当温度为超高温度状态时，基频甚至会增加至1 000 Hz。随着温度升高至超高温度时(即S≫1)，高阶模态已经参与其中，这就会导致响应变得愈加复杂。

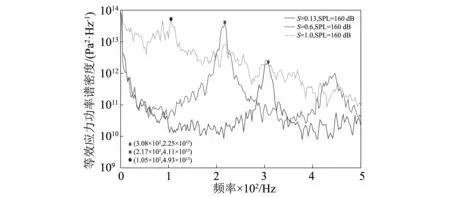
图12 SPL=160 dB屈曲前应力功率谱密度Fig 12. Stress PSDs at SPL=160 dB and S≤1

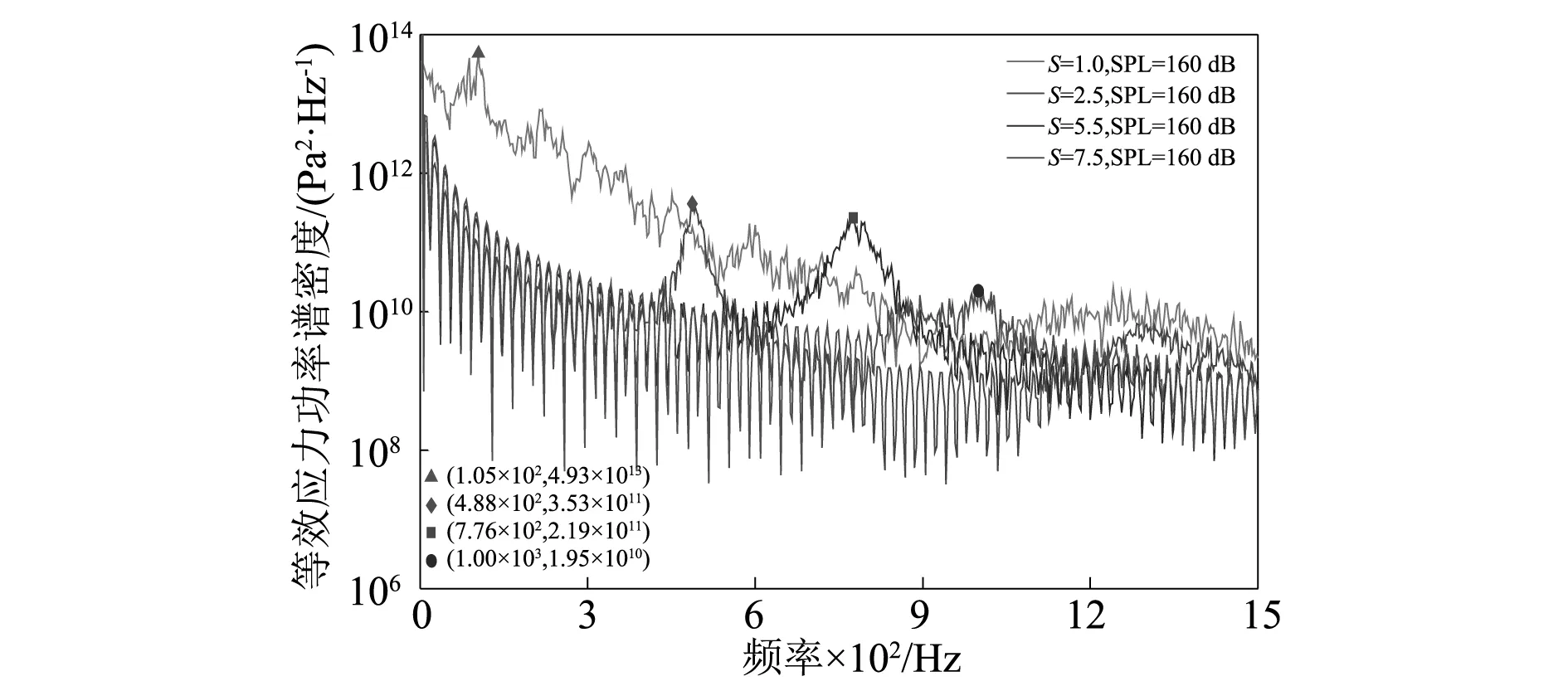
图13 SPL=160 dB屈曲后应力功率谱密度Fig 13. Stress PSDs at SPL=160 dB and S≥1

在实际工况下，由于作用在层合板上的是相互耦合地全部变化的热声载荷，这就促使层合板对两种载荷的动态响应会呈现出特殊的性质，即不是简单地两种载荷作用下响应线性叠加，这一点在实际应用中需要予以重视。

2.6 C/SiC层合薄板在热声载荷作用下的疲劳寿命

由于实际工况下航空薄壁结构多处于屈曲后高温度载荷与强噪声载荷的双重作用环境中运行，此时层合薄板内部已由屈曲前的拉应力转变为压应力，且同等压缩载荷造成的损伤要比拉伸载荷小。为更形象地判断结构处于这一阶段工况下热载荷与声载荷对结构作用下层合板的应力分布，本文分别提取C/SiC层合板屈曲后SPL=160 dB噪声载荷与三种超高热载荷组合激励下结构的等效应力雨流循环矩阵图加以直观展现结构内部应力幅值及应力均值变化，为后续寿命分析提供参考，如图14所示。

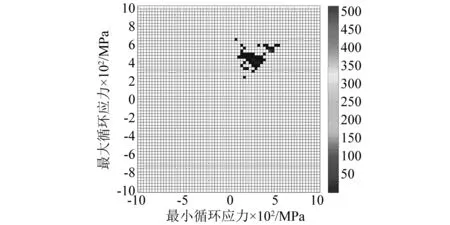
(a) S=5.5, SPL=160 dB

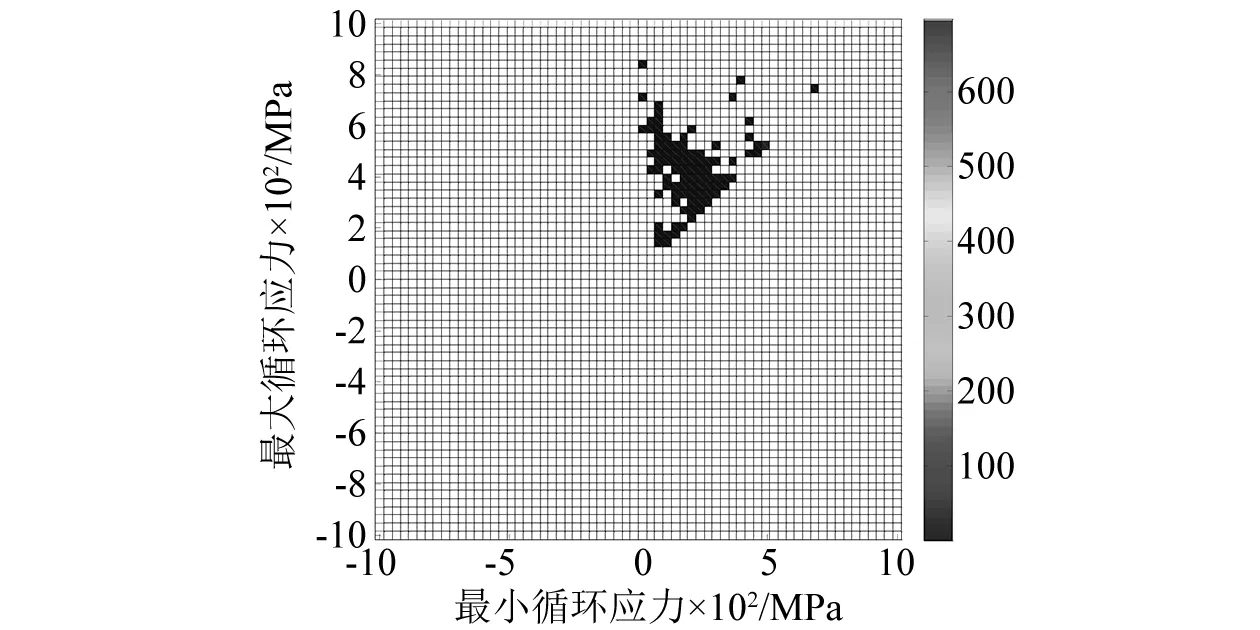
(b) S=6.5, SPL=160 dB

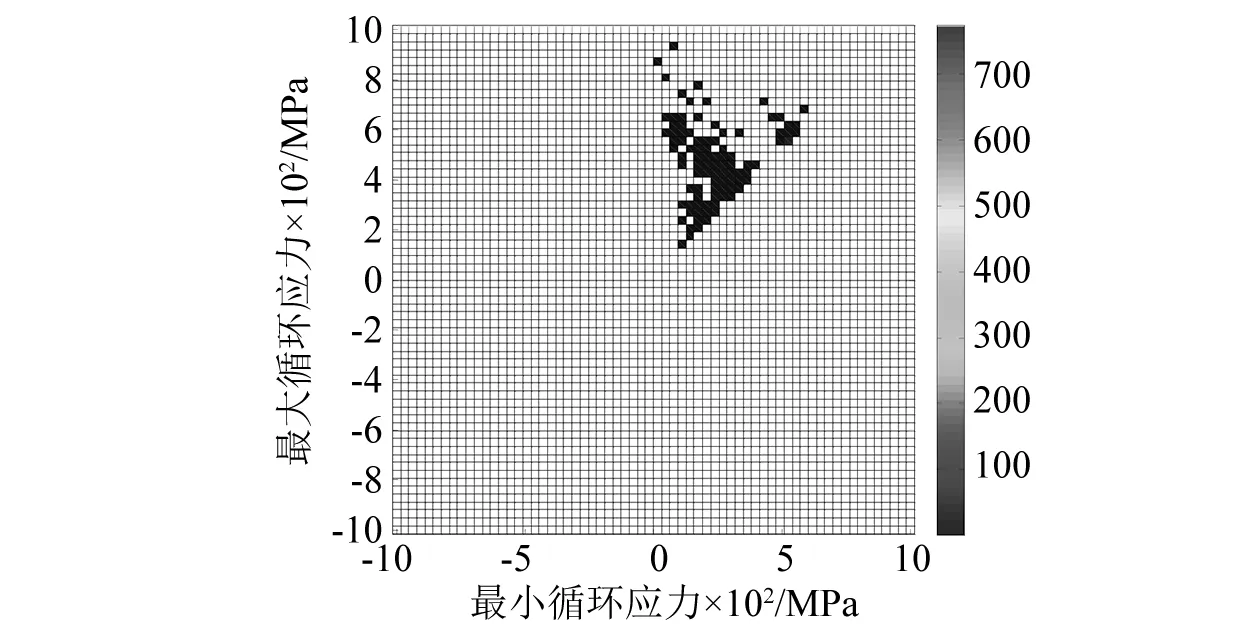
(c) S=7.5, SPL=160 dB图14 雨流循环矩阵Fig.14 RFM at three thermal-acoustic loadings

当S足够大时层合板结构围绕屈曲后平衡位置振动。相应地，表现在雨流循环矩阵图14上为只有右上角的循环块。随着温度逐渐增加，应力循环的幅值也逐渐增大，对应的均值也逐渐增大，循环块向右上方移动且呈发散状。

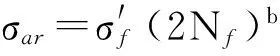
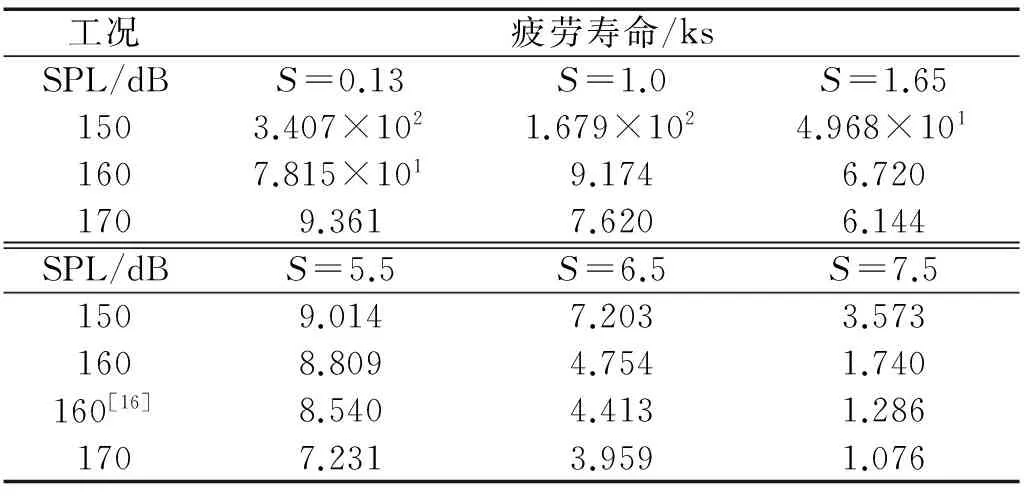
表3 各工况下C/SiC层合板热声疲劳寿命

由表中信息可知，当温度较小(S≤1.65)时，屈曲后的热声疲劳寿命约为屈曲前的8.60%～65.63%；而在超高温度载荷下，如S=7.5时结构热声疲劳寿命约为S=5.5时的14.88%～39.64%；S=6.5时结构热声疲劳寿命约为S=5.5时的53.97%～68.17%，从这些规律以及表中数据可知热载荷和声载荷对层合板结构疲劳寿命的影响程度不同。

当声压级不变而温度逐渐升高时，层合板寿命先经过一个急剧减小后略有提高至超高温载荷时又开始缓慢下降，这是由于结构停止跳变后，随着温度逐渐升高超过材料制备温度时，疲劳循环均值增加对寿命的影响较大，疲劳寿命下降，并且温度越高，寿命越低。相对于屈曲系数为S=5.5等超高温环境工况下C/SiC复合材料层合板结构的热声寿命而言，屈曲系数为S=0.13下该结构疲劳寿命随声载荷逐渐增大而下降速率较大，随着温度升高，疲劳寿命下降趋势逐渐变缓，这是由于C/SiC层合板结构的制备温度较高(约为1 000 °C)，在纤维轴向方向上碳纤维热膨胀系数低于碳化硅基体热膨胀系数，沿纤维径向方向上碳纤维热膨胀系数高于碳化硅基体热膨胀系数，故当温度低于制备温度时结构内部存在热残余拉应力，从而导致碳化硅基体沿纤维轴向方向易开裂且在一定程度上也降低了界面层的结合强度，这就致使结构在外界载荷作用下存在更大的界面滑动损伤；随着温度逐渐接近制备温度时，层合板内部热残余拉应力逐渐消减直至为0，这一过程中热残余拉应力对寿命的影响也就逐渐消退；随着温度的进一步升高，层合板内部出现的热残余压应力对损伤的抑制作用逐渐变强；与此同时，层合板内部纤维与基体之间的界面相可能因发生一定程度的变化而表现出对损伤疲劳的促进作用，界面相对损伤的促进作用和残余压应力对损伤的抑制作用相互耦合导致层合板结构的寿命降低速率相较低于制备温度时的结构寿命下降速率逐渐变缓；当温度不变而声压级逐渐增加时，结构的疲劳寿命下降。这是由于随着声压级增加，疲劳循环幅值的增加引起了结构内部损伤增加。

3 结 论

基于有限元法得到的热声载荷联合作用下的碳纤维增强碳化硅基体复合材料层合板结构动态响应，结合Morrow平均应力模型和Miner线性损伤估算结构疲劳寿命，得到如下结论：

(1) 层合板在不同温度下的刚度变化趋势不同。随着作用于结构上的温度载荷由屈曲前温度逐渐增大至临界屈曲温度时，结构出现软化现象，其刚度减弱，导致该层合板结构基频呈现逐渐降低趋势；而后随温度继续增大，结构伴随硬化现象，此时刚度逐步增强，结构基频又呈现逐渐增大趋势；而随着温度持续升高至远高于临界屈曲温度时，此时结构的热声响应有多重模态同时参与其中，故当层合板结构做抗热声疲劳设计时应该分析其处于工况温度下的热模态，以达到尽量避开其热模态基频目的。

(2) 在结构处于屈曲系数S=0.13而声压级逐渐增大状态下时，结构呈现弱非线性响应；结构处于屈曲后状态时，作用于结构的声压级足够大就可使该层合板结构出现跳变响应，此时层合板中心处的等效应力幅值迅速增加，这会进一步降低结构疲劳寿命。

(3) 由雨流循环矩阵云图可以直观地分析层合板结构处于屈曲后超高温载荷作用下的非线性响应变化规律。在一定噪声载荷下，随温度持续升高，应力循环幅值增大的同时应力循环均值亦明显增大，即层合板在超高温载荷激励时静强度对外载荷的敏感性逐渐变强。

(4) 超高温度与临界屈曲温度附近层合板热声疲劳寿命随温度变化趋势不同。当温度较小(S≤1.65)时，屈曲后的热声疲劳寿命约为屈曲前的8.60%～65.63%；而在超高温度载荷下，如S=7.5时结构热声疲劳寿命约为S=5.5时的14.88%～39.64%；S=6.5时结构热声疲劳寿命约为S=5.5时的53.97%～68.17%。层合板处于屈曲前，随着声压级的增大，结构寿命呈现数量级下降，这说明此时声载荷对层合板结构寿命影响较大；层合板处于屈曲后状态时，随温度升高结构寿命降低速率远大于随声压级增大结构寿命的下降速率，这说明此时温度是影响结构疲劳寿命的重要因素。从微观可以解释疲劳寿命估算值在不同工况下变化情况，验证了本文所用预测疲劳寿命研究方法应用于热声作用下的C/SiC层合薄板结构的可靠性；计算寿命与参考文献结果差异可解释为本文考虑了平均应力对寿命的影响，这从侧面亦可说明本文计算寿命方法可靠性。

[1] 吴振强，任方，张伟，等. 飞行器结构热噪声试验的研究进展[J]. 导弹与航天运载技术，2010, 306(2): 24-30. WU Zhenqiang, REN Fang, ZHANG Wei, et al. Research advances in thermal-acoustic testing of aerocraft structures[J]. Missiles and Space Vehicles, 2010, 306(2): 24-30.

[2] 杨忠学.3D-C/SIC的高温拉伸蠕变性能[D]. 西安：西北工业大学，2002.

[3] 张立同，成来飞，徐永东.新型碳化硅陶瓷基复合材料的研究进展[J]. 航空制造技术，2003 (1):24-32. ZHANG Litong, CHENG Laifei, XU Yongdong. Progress in research work of new CMC-SiC[J]. Aeronautical Manufacturing Technology, 2003 (1):24-32.

[4] 张建艺.陶瓷基复合材料在喷管上的应用[J].宇航材料工艺，2000,30(4):14-16. ZHANG Jianyi. Ceramic matrix composite applications in nozzle [J]. Aerospace Materials and Technology, 2000, 30(4):14-16.

[5] CLARSON B L. Review of sonic fatigue technology [R]. NASA CR4587, 1994.

[6] WOLFE H F, SHROGER C A, BROWN D L, et al. An experimental investigation of nonlinear behavior of beams composite plates excited to high levels of dynamic response [R]. Wright Lab, WL-TR-96-3057, Wright-Patterson AFB, OH, Oct. 1995.

[7] ISTENES RR, RIZZI S A, WOLFE H F. Experimental nonlinear random vibration results of thermally buckled composite panels [C]∥ Proceedings of 36th Structures, Structural Dynamics, and Materials Conference. Washington, DC: AIAA, 1995: 545-550.

[8] DAFEDAR J B，DESAI Y M．Thermomechanical buckling of laminated composite plates using mixed higher-order analytical formulation [J]．Journal of Applied Mechanics，2002,69(4)：790-799．

[9] DAFEDAR J B, DESAI Y M．Stability of composite and sandwich struts by mixed formulation [J]．Journal of Engineering Mechanics，2004,130(7):762-770.

[10] IBRAHIM H H, TAWFIK M, NEGM H M. Random response of shape memory alloy hybrid composite plates subject to thermo-acoustic loads[J]. Journal of Aircraft, 2008, 45(3): 962-970.

[11] 钟轶峰，余文斌.反对称角铺设复合材料层合板热后屈曲和模态跃迁分析[J].振动与冲击,2011,30(8): 169-174. ZHONG Yifeng, YU Wenbin. Thermal post-buckling and mode jumping analysis of antisymmetric angle-ply composite laminates [J]. Journal of Vibration and Shock, 2011, 30(8): 169-174.

[12] 杨雄伟，李跃明，耿谦. 基于混合FE-SEA法的高温环境飞行器宽频声振特性分析[J]. 航空学报, 2011,32(10): 1851-1859． YANG Xiongwei, LI Yueming, GENG Qian. Broad-band vibro-acoustic response of aircraft in high temperature environment based on hybrid FE-SEA[J]. Acta Aeronautica et Astronautica Sinica, 2011,32(10): 1851-1859．

[13] SHA Y D, GAO Z J, XU F, et al. Influence of thermal loading on the dynamic response of thin-walled structure under thermo-acoustic loading[J]. Applied Mechanics and Materials, 2011(2/3): 876-881.

[14] SHA Y D, WEI J, GAO Z J. Nonlinear response and fatigue life prediction of thin-walled structures under thermo-acoustic loadings[J]. Applied Mechanics and Materials, 2012(157/158) : 1204- 1211.

[15] MEI C, DHAINAUT J M, DUAN B, et al. Nonlinear random response of composite panels in an elevated thermal environment [R]. Air Force Research Laboratory, Wright-Patterson Air Force Base, OH, AFRL-VA-WP-TR-2000-3049, October 2000.

[16] ZHOU Yadong, WU Shaoqing, TAN Zhiyong, et al. Temperature-dependence of acoustic fatigue life for thermal protection structures[J]. Theoretical and Applied Mechanics Letters, 2014,4(2):27-31.

Dynamic response analysis and fatigue life prediction ofC/SiC thin laminated plate under thermal-acoustic loadings

BAI Wenjun, SHA Yundong , LI Huashan，TANG Xiaoning

(Liaoning Province Key Laboratory of Advanced Measurement and Test Technologyof Aviation Propulsion System Liaoning, Shenyang Aerospace University, Shenyang 110136, China )

In view of the poor working environment of thin walled structures under thermal-acoustic loading conditions that are extremely easy to induce the buckling and acoustic fatigue and affect the stability and service life of components. A thin C/SiC composite laminated plate with four edges clamped was taken as an object examined. The finite element method was used to calculate the nonlinear random responses of the plate under various combinations of sound pressure levels and temperatures and typical thermal-acoustic motions were achieved. The response characteristics of the structure during buckling and post buckling were analysed and the typical nonlinear vibration response characteristics were summarized. In consideration of the high specific strength and special structural fatigue damage mechanism of composite laminated plates, the rain flow method was improved to count the stress responses of laminated plates under the condition of high temperature and loud noise. Making use of the performance data of material obtained in symmetrical cycle fatigue tests, the equivalent life formula for estimating the fatigue life of composite laminated plates was fitted, in which the mean stress effect was considered and the Palmgren-Miner linear cumulative damage criterion was adopted.

C/SiC composite laminated plate; thermal-acoustic loading; stress dynamic response; rainflow counting; fatigue life

航空基础科学基金资助项目(02C54007)

2016-01-25 修改稿收到日期： 2016-04-05

白文君 男，硕士生，1990年10月生

沙云东 男，博士，教授，1966年11月生

V214.8

A

10.13465/j.cnki.jvs.2017.10.013