核燃料棒温度场和系统熵增分布计算与研究
张功伟,张钧波,张 敏
(1.南京理工大学能源与动力工程学院, 江苏南京210094;2.南京师范大学泰州学院,江苏泰州225300)
核燃料棒温度场和系统熵增分布计算与研究
张功伟1,张钧波2,张 敏1
(1.南京理工大学能源与动力工程学院, 江苏南京210094;2.南京师范大学泰州学院,江苏泰州225300)
基于热力学第二定律以及压水核反应堆燃料棒稳态传热偏微分方程的一般形式,通过熵增的数值计算,讨论分析燃料棒内热量的传递过程和方向,以及能量品质的得失。先对典型二维矩形域传热问题进行数值计算,并采用解析解对该数值方法进行了验证。然后对含有内热源的单根燃料棒进行传热计算,讨论其温度和熵增分布情况,通过熵增云图分析可以展现燃料棒内热量的传递过程和品质变化,为核反应堆热工设计提供有益参考。
压水核反应堆;燃料棒;熵增
保证核反应堆安全运行一直是近代核科学研究的重要课题,而研究燃料棒的热量传递过程是其中一项重要内容。对于压水核反应堆燃料棒传热系统的计算分析,一般都是从热力学第一定律的角度出发[2],通过数值传热学求解燃料棒内温度场分布,或是应用流体力学计算软件对燃料组件内通道进行三维数值模拟[3,4],从而获得燃料组件与外围冷却剂对流换热的详细状况。然而对于燃料棒内热量传递的方向性,以及能量品质得失的研究也十分必要的。
本文将从热力学第二定律出发,通过计算系统熵增,重点讨论燃料棒内热量传递过程的方向性。首先采用一个简单的二维矩形域传热问题,对比分析求解出的数值解和解析解,并通过函数极小值求解,确定热量的极值点,从而验证该数值方法的正确性。最后以单根燃料棒为模型,计算在核反应堆正常工况下燃料棒的熵增分布情况,进而可以从热量传递和能量品质变化的角度进行更加合理的热工设计,即更加快速有效的导出燃料棒内反应热,保证反应堆的安全运行。
1 基本计算方程
在广义正交曲线坐标系内一般形式的非稳态导热微分方程为:
(1)
式中:qv为单位体积的内热源,k为材料的热导率。系数a=a1a2a3,根据所选坐标系的不同,尺度系数a1、a2、a3既可以是常数,也可以是坐标的函数。
假设系统内部的过程是可逆的,则熵增函数可以表示为:
(2)
式中:δq为热传递过程中微元热量。
2 二维矩形域算例
2.1 方程的求解
在直角坐标系内,选取一长为a,宽为b的矩形为计算域,假设该矩形常物性、无内热源,根据公式(1),其稳态导热微分方程可简写为:
(3)
其边界条件定为:
T(x,y)=x+y+xy
(4)
数值计算求得系统达到稳态时的温度Ta为:
(5)
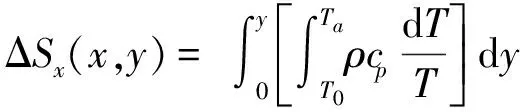
(6)
系统总熵增为:
(7)
积分式(7)有如下两种形式:
(8)
对式(8)分别进行一次、二次求导,可求得系统总熵增随x和y的变化率:
(9)
2.2 系统熵增的计算与分析
取系统ρcp=1,初始温度T0=2℃,并取矩形几何尺寸为a=2 m,b=1 m。通过公式(5)可以得到该矩形域每个点的温度值,获得温度场,同时通过式(6)和式(7),运用数值方法积分得到矩形域熵增的分布情况。
如图1矩形域温度分布云图所示,随着坐标x和y的不同,每一点的温度值不断变化,温度最低点出现在原点,然后随着x和y的增大,最终在顶点(2 , 1)处达到最大值。
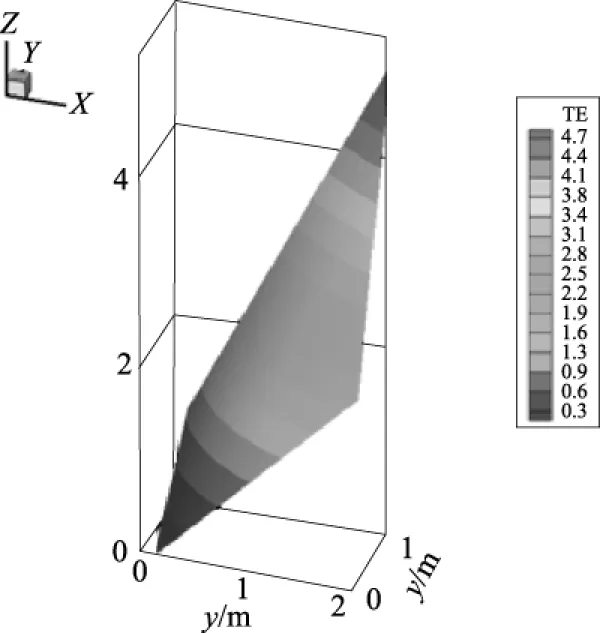
图1 矩形域的温度分布图Fig.1 Temperature distribution of rectangular region
根据式(6),系统局部熵增变化情况可从沿x截面和y截面两个方向分析,如图2所示。从图中可以看到系统局部熵增从x=0截面到x=2截面的变化过程,从开始的Ta
图3为该矩形域总熵增的变化云图。对比图2,这里可以更清晰看出,在x=0及y=0截面处,Ta
根据二元函数极值准则,可以求得系统熵增的极值点大约位于点(1.0 , 0.5)附近,此时总熵增值为-0.27。
3 燃料棒内的熵增计算
前面通过一个简单的传热问题,验证了该方法的合理性和准确性,这里将对单根燃料棒内的熵增问题进行分析。由于轴对称性,一根为常物性圆柱形燃料棒的温度场与角度无关,则根据公式(1),其稳态导热微分方程可简写为公式(10):
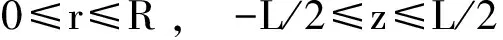
(10)
在核反应堆正常运行工况下,燃料棒内的热源项通常可表示为:
(11)
建模时的坐标原点取燃料棒中心,其上下壁面为定温边界条件,在侧面r=R燃料棒包壳处与外围冷却剂进行对流换热,即模型的边界条件可数学描述为:

图2 系统分别沿x,y截面局部熵增Fig.2 The local entropy of system along the section x,y
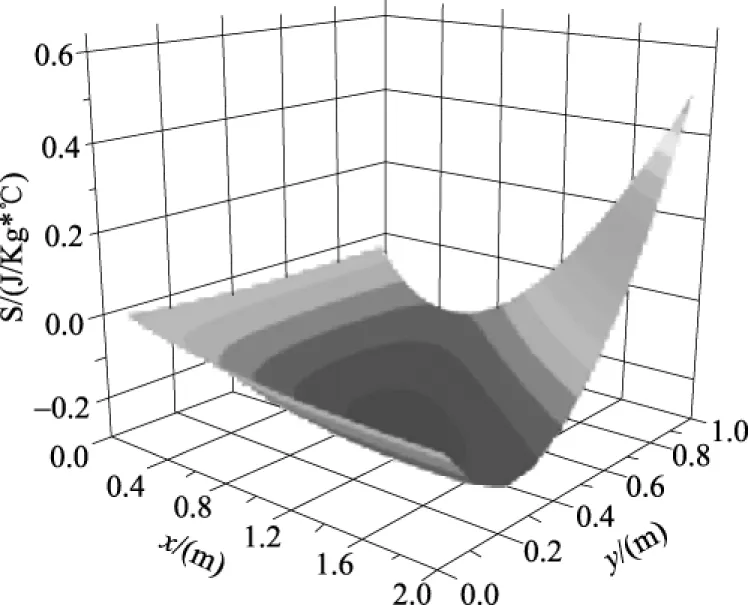
图3 系统沿xy平面的总熵增Fig.3 Total entropy of system along plane xy
(12)
式中:Tw(z)为r=R处的温度,即Tw(z)=T(R,z);Tf(z)为流体温度,其线性化形式为:
(13)
从而可以求得此时燃料棒最终的稳态温度为,

(14)
同样,这里假设燃料棒的初始温度为T0,则在其达到稳态时,系统的局部熵增可分成沿rφ和rz截面两个方向,分别表示为式(15)和式(16),总熵增为式(17)。

πρcpr2lnT0
(15)
(16)
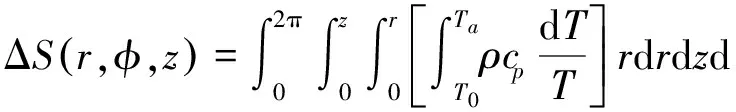
πρcpr2zlnT0
(17)
这里选取单根燃料棒具有代表性的一段作为数值模型,其高度为L=30 mm,半径R=5 mm,初始温度T0=(T1+T2)/2=568 K,其他各项热工参数如表1所示。
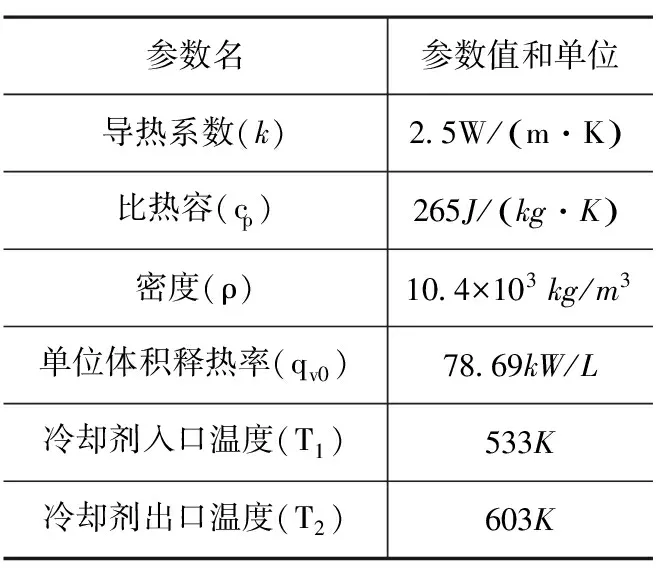
表1 燃料棒热工参数
由于对称性,取二分之一圆柱体燃料棒作为计算模型,图4为其在rφ和rz截面的温度场云图,很容易看出燃料棒在这两个平面的温度场均以原点为中心向外环形扩散,越靠近外围温度值越低,在中心附近温度值最高。因为其温度分布规律与角度无关,所以这里在rφ截面的熵增分析也只考虑随半径的变化情况。
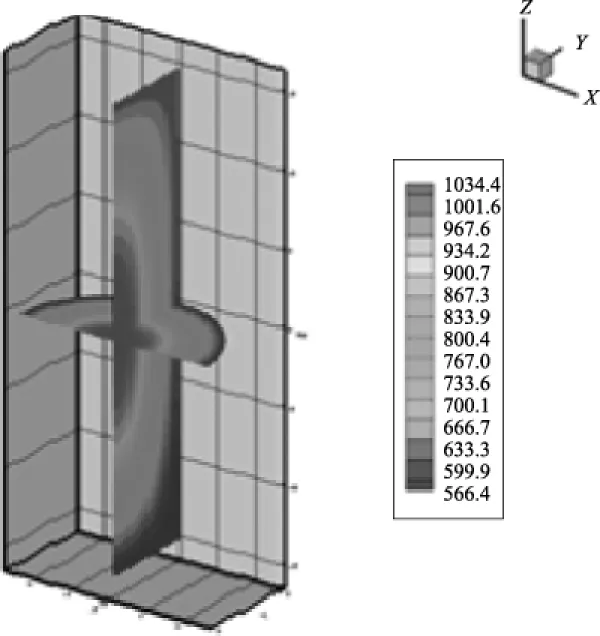
图4 燃料棒rφ,rz平面的温度分布示意图Fig.4 Temperature distribution of plane rφ,rz


图5 底面沿半径方向的温度及局部熵增曲线图Fig.5 Temperature distribution and local entropy of underside along radius direction
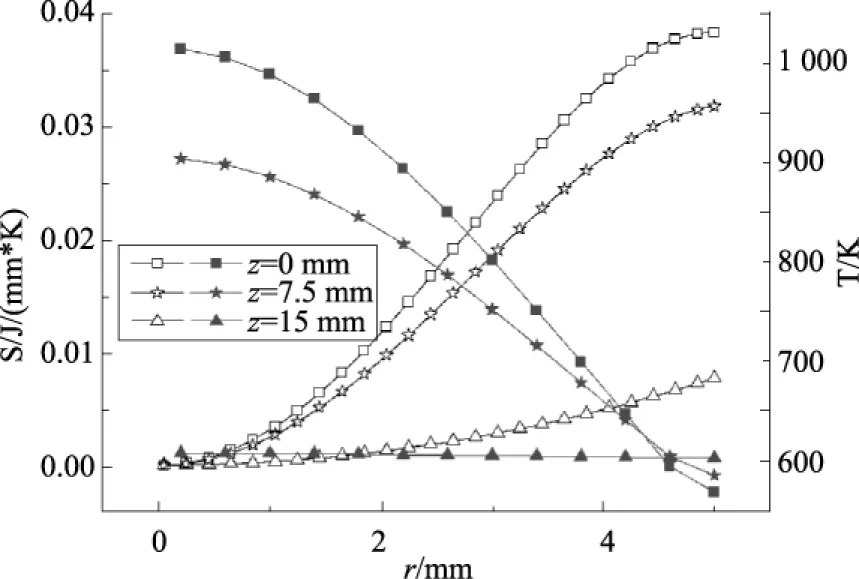
图6 不同高度沿径向的温度及局部熵增曲线图Fig.6 Temperature distribution and local entropy of different height along radius direction
从图7的云图可以更清晰看出上述的变化趋势,由下往上,在底面有Ta 图7 燃料棒xz平面的局部熵增示意图Fig.7 Local entropy of plane xz 对于压水核反应堆燃料棒传热系统的计算分析,温度场的求解固然十分重要,但热传递过程中熵增的计算也具有极大意义和实用价值。本文基于热力学第二定律,从温度分布和熵增两个角度分析压水堆燃料棒正常运行工况下的传热过程,尤其在热量传递的方向性上取得可信结果,从而可以对传热过程的优劣程度进行可靠性评估,也可以从能量品质变化的角度优化反应堆热工设计,对于进一步提高反应堆运行的安全性有一定参考价值。 [1] 陈文振,于雷,郝建立.核动力装置热工水力[M].北京:中国原子能出版社,2013. [2] 刘会娟,张敏,彭文杰.圆柱形带反射层反应堆的数值传热计算[J].核科学与工程,2010,30(1):42-47. [3] 罗磊,陈文振,陈志云,等.单个燃料元件热工水力三维数值模拟[J].海军工程大学学报, 2011, 23(1): 63-66[4] 宋磊, 郭赟, 曾和义. 板状燃料组件入口堵流事故下流场和温度场的瞬态数值计算[J]. 核动力工程, 2014, 35(3):6-10 [5] Zhang, M. Modeling of Radiative Heat Transfer and Diffusion Processes Using Unstructured Grid [D]. Cookeville: Tennessee Technological University, 2000. [6] Patankar, S. V. Numerical Heat Transfer and Fluid Flow [M]. New York: Hemisphere Publishing, 1981. Study on the Distribution of Temperature and Entropy for a Reactor Fuel Rod ZHANG Gong-wei1, ZHANG Jun-bo2, ZHANG Min1 (1.School of Power & Energy Engineering, Nanjing University of Science & Technology, Nanjing, Jiangsu Prov. 210094;2. Taizhou College, Nanjing Normal University, Taizhou, Jiangsu Prov.225300) According to the second law of thermodynamics and steady partial differential equations for heat transfer in a fuel rod of pressurized water reactor, entropy production of the rod is numerically calculated to discuss the process and direction of heat transfer, as well as the gain and loss of energy in the fuel rod. A typical heat transfer case for 2D rectangle region is conducted firstly and the analysis solution is used to validate the accuracy and robustness of the code. Finally, a single fuel rod with an internal heat source is numerically studied. The distribution for temperature and entropy in the rod is discussed. The contour map of entropy distribution indicates that the numerical method is able to reveal the transfer and variation of heat transfer in the rod clearly. It is somewhat useful for thermal performance design of nuclear reactor. Pressurized water reactor; Fuel rods; Entropy production 2016-12-29 张功伟(1991—),男,江苏人,硕士研究生,从事计算流体力学及计算传热学研究方向 TL331 A 0258-0918(2017)02-0333-07
4 结论

