慢化剂温度系数为正时硼浓度限值研究

高 鑫，刘国明,蔡光明

(1.中国核电工程有限公司，北京100840 2. 福建福清核电有限公司，福州福清350318)



慢化剂温度系数为正时硼浓度限值研究

高 鑫1，刘国明1,蔡光明2

(1.中国核电工程有限公司，北京100840 2. 福建福清核电有限公司，福州福清350318)

负慢化剂温度系数是压水堆自稳自调特性的基础，也是压水堆设计和运行的安全要求。在一定的技术规范的框架内，启动阶段的低功率状态下，存在一定的正慢化剂温度系数对运行调控是不利的。因而必须根据零功率试验结果提出保证慢化剂温度系数为负的最高硼浓度限值，以临时运行指令的形式要求运行人员满足这一限值条件。本文通过对慢化剂温度系数与硼浓度关系的研究，提出慢硼系数这一概念，并研究了慢硼系数与功率、燃耗、硼浓度的关系，进而得到了慢硼系数修正公式。最后给出了保证慢化剂温度系数为负的最高硼浓度限值的计算公式及速算公式，并验证了速算公式的保守性和适用性。

慢化剂温度系数；硼浓度限值；慢硼系数

负慢化剂温度系数是压水堆自稳自调特性的基础，也是压水堆设计和运行的安全要求。在一定的技术规范的框架内，在启动阶段的低功率状态下，存在一定的正慢化剂温度系数对运行调控是不利的。

在核反应堆启动物理零功率试验中，通过测量和修正，得到BOL-HZP-ARO临界硼下慢化剂温度系数(MTC)。如果MTC为正，为了堆芯安全，最有效方法是降低堆芯临界硼浓度使MTC变负。为了降低堆芯临界硼浓度，需插入功率补偿棒，然而功率补偿棒长期插入，对于启动物理功率台阶试验以及堆芯后续平稳运行都会带来额外的问题。

堆芯临界硼浓度，不仅与控制棒插入有关，还与堆芯功率台阶、堆芯燃耗以及堆芯燃耗产生Xe-Sm浓度相关。当堆芯临界硼浓度随着功率台阶、堆芯燃耗以及Xe-Sm浓度下降到可使MTC为负情况下，就可以不插入功率补偿棒。

本文提供了一种方法，在参考状态MTC测量值为正时，确定使MTC为负的最大硼浓度限值。只要保证堆芯临界硼浓度低于限值，就可确保MTC为负。该方法基本思路如下：根据硼浓度与慢化剂温度系数线性关系，总结出可以在工程上加以应用的硼浓度限值速算公式，并对该公式适用性加以验证，从而可以得出零功率试验慢化剂温度系数为正时硼浓度最高限值。

1 慢硼系数定义

根据硼浓度与慢化剂温度系数的线性关系，提出硼浓度限值公式：

(1)

式中:BORE限值：测量慢化剂温度系数时的硼浓度，通常为HZP-ARO临界硼浓度；

ΔMTC：期望慢化剂温度系数的修正量，由于通常期望将慢化剂温度系数修正为0，ΔMTC即为实测的慢化剂温度系数；

CMB(BU，P，BORE)：慢硼系数，硼浓度单位变化(变化1ppm)所引起慢化剂温度系数的改变，单位为pcm/(℃·ppm)。

(2)

考虑到慢化剂温度系数在测量时，基本在基准温度下进行，并且温度变化包含在功率变化之内，因而忽略温度对CMB的影响。

在给定堆芯状态(功率P燃耗BU给定)的前提下，由式(2)可知慢化剂温度系数与硼浓度的变化呈现近似线性关系，因而慢硼系数CMB即为拟合直线的斜率，为恒定值。

2 慢硼系数与功率燃耗硼浓度关系

2.1 慢硼系数与功率关系

首先研究慢硼系数随功率变化的关系，由图1和表1可以看出，给定燃耗，慢硼系数随功率增大而增大，和功率近似成二次关系，拟合公式为：

CMB=0.003 9P2+0.004 8P+0.022 534

(3)

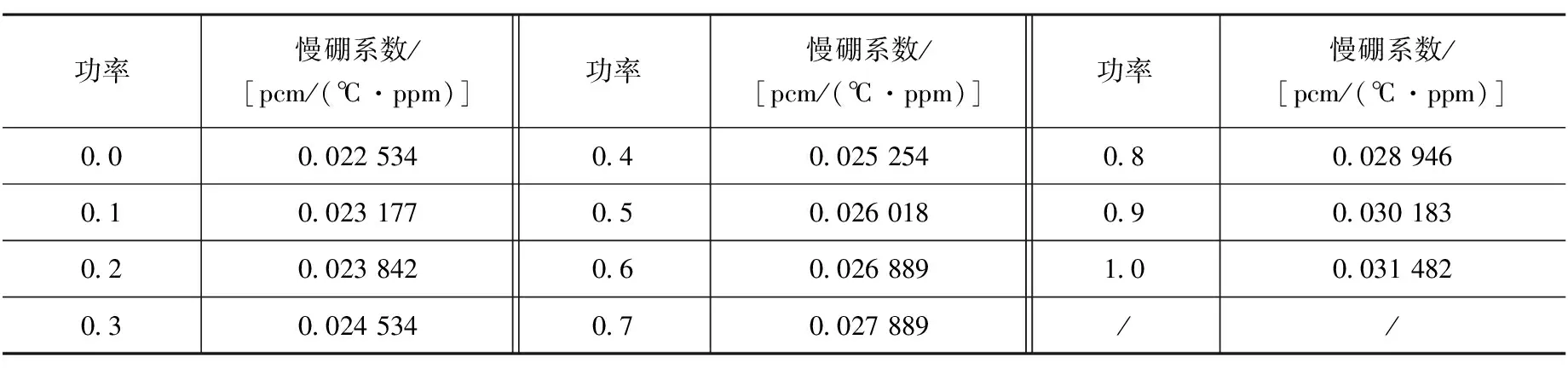
表1 不同功率下慢硼系数(BU=0)

图1 不同功率下慢硼系数(BU=0)Fig.1 The moderator temperature-boron coefficient for different power(BU=0)

2.2 慢硼系数与燃耗关系

下面研究慢硼系数随燃耗变化的关系，在功率等于0，硼浓度在1082～1282ppm范围内，进行各燃耗点下慢硼系数的计算，结果如 图2 所示。

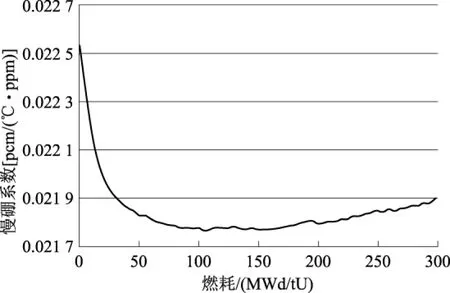
图2 不同燃耗下慢硼系数(P=0)Fig.2 The moderator temperature-boron coefficient for different burnup(p=0)

由图2可以看出慢硼系数随燃耗的变化关系，在燃耗为0～100MWd/tU时，慢硼系数随燃耗增大而减小，100～200MWd/tU阶段，慢硼系数几乎无变化，200MWd/tU-EOL阶段，慢硼系数随燃耗增大而逐渐增大。

由于在测量慢化剂温度系数时一般为零功率试验阶段，燃耗不会超过20MWd/tU，因而对0～20MWd/tU的曲线进行拟合，得到结果如图3所示。

图3 不同燃耗下慢硼系数(P=0)Fig.3 The moderator temperature-boron coefficient for different burnup(P=0)

由图3可以看出，给定功率，慢硼系数随燃耗增大而减小，和燃耗近似成三次关系(0～20MWd/tU)。拟合公式为：

CMB= 2×BU3×10-8+4×BU2×10-7-4×

BU×10-5+0.022 534

(4)

2.3 慢硼系数与硼浓度关系

下面研究慢硼系数与硼浓度的关系，分别计算不同硼浓度区间的慢硼系数进行计算，得到结果如图4所示。

图4 不同硼浓度下慢硼系数(P=0) Fig.4 The moderator temperature-boron coefficient for different boron(P=0)

实线——硼浓度区间：1282～1082ppm，平均硼浓度为1182ppm；

图4可以看出，随着硼浓度增高，慢硼系数逐渐减小，慢硼系数CMB随硼浓度减小量基本成线性，每增加100ppm硼，慢硼系数减少0.00083，由此得到修正公式：

拟合公式为：

CMB=CMB(BOREstandard)-8.3×10-6

(BOREreal-BOREstandard)

(5)

2.4 慢硼系数修正公式

综合以上论述，我们得到慢硼系数随功率、燃耗以及硼浓度变化的拟合公式：

CMB=CMB基准-8.3×10-6ΔBORE+

3.9×10-3ΔP2+4.8×10-3ΔP+

2×10-8ΔBU3+4×10-7

ΔBU2-4×10-5ΔBU

(6)

基于福清1号机组，基准状态为BORE=1182ppm，BU=0，P=0,

CMB基准=0.022 534 pcm/(℃·ppm)。

3 慢硼系数的应用及速算公式确定

3.1 硼浓度限值公式应用

我们来看第1节给出硼浓度限值公式：

(7)

由公式可以看出，CMB取值越小，得到的硼浓度限值越小越保守，为了方便工程计算因而可以对公式(1)加以简化，采用一个保守的CBM(包络)。

(8)

在工程实践中，既可以采用所给出的拟合公式来进行修正，也可以通过给出一个保守的包络值直接应用。由以上分析可以看出，在全寿期，全部功率水平下，得到的最小慢硼系数的包络值为0.021 pcm/(℃·ppm)。

如：试验测量慢化剂温度系数为 1.275 pcm/℃，为保证慢化剂温度系数为负，ΔMTC=1.275 pcm/℃，慢硼系数CMB取包络值0.021 pcm/(℃·ppm)，测量慢化剂温度系数时硼浓度为1182ppm，计算得到硼浓度限值为1121.3ppm，即堆芯硼浓度不超过此硼浓度，即可保证MTC为负。

3.2 慢硼系数引起硼浓度限值敏感性分析

对慢硼系数引起硼浓度限值变化进行敏感性分析如表2所示。

表2 不同慢硼系数下的硼浓度限值

由表2可以看出，无论慢硼系数取0.21 pcm/(℃·ppm)作为包络值甚至更加保守的0.20 pcm/(℃·ppm)为包络值，所引起硼浓度差异均在10ppm之内，可见合理地选取CMB(包络)，既能比较方便计算出硼浓度限值，又与真实CMB计算得到的限值差别不会很大。

3.3 硼浓度限值速算公式

为更加保守起见，可以推荐慢硼系数为0.02 pcm/(℃·ppm)作为CMB(包络)。这样得到的硼浓度限值的速算公式为：

BORE限值=BOREnow-50×ΔMTC

(9)

这样便得到一种方法，在零功率物理试验ARO状态MTC为正时，确定保证MTC为负的最大硼浓度限值。该方法步骤如下：

(1) 确定ΔMTC，即零功率试验时慢化剂温度系数超过0的数值；

(2) 将得到的ΔMTC乘以50，确定硼浓度限值偏差；

(3) 用当前临界硼浓度减去硼浓度偏差即可得到最大硼浓度限值。

这样得到的公式既比较保守，又使得在工程上的应用比较方便。

4 修正公式及速算公式验证

4.1 修正公式准确性验证

以福清核电厂1号机组启动物理试验为例：表3为程序的计算值、试验值与偏差。

表3 福清核电厂1号组件零功率试验慢化剂温度系数设计值及试验值偏差

根据物理试验实际测量结果，得到设计值和试验值偏差为-2.084 pcm/℃，为了保守起见，偏差选择在-2.5pcm/℃。

由此计算出使得堆芯慢化剂温度系数计算值在-2.5 pcm/℃(相应试验值为-0.416 pcm/℃)时得到慢化剂温度系数偏差ΔMTC=1.275-(-0.416)=1.691 pcm/℃，分别进行硼浓度限值搜索计算和利用修正公式对硼浓度限值进行计算，得到的硼浓度限值差别见表4。

表4 搜索计算与修正公式计算得到各燃耗点各功率水平下的硼浓度限值之差

* 堆芯燃耗 MWd/tU, ** 堆芯相对功率水平，*** 硼浓度。

从上述表格可以看出，搜索硼浓度得到的限值与修正公式得到的硼浓度限值大小相近，可以说明修正公式得到的计算值是准确的。由于修正公式单独考虑了燃耗、功率和硼浓度的修正量，并没有考虑他们的耦合关系，因而，功率和燃耗偏离参考点越远，得到差别越大，产生偏差的原因是考虑了保守性的缘故。所以燃耗和功率比较小时，修正公式得到结果比较准确；修正公式得到硼浓度绝大多数小于搜索硼浓度得到的限值，可以说明修正公式得到的限值是保守的。

4.2 速算公式保守性验证

慢化剂温度系数测量通常在HZP，BU=0时刻，由福清核电厂零功率启动物理试验数据得到此时临界硼浓度为1182ppm，速算公式得到硼浓度限值为1097.45ppm(使得慢化剂温度系数计算值为-2.5 pcm/℃，相应试验值为 -0.416 pcm/℃)，搜索得到结果为1110.2ppm，速算公式得到结果小于程序搜索得到的结果，比较保守。

4.3 慢硼系数包络值验证

对不同堆型，不同循环加以计算，验证该包络值是否可以包络其他的堆型和循环。

首先对177和121堆型收循环慢硼系数随燃耗变化加以计算，得到如图5、图6所示结果。

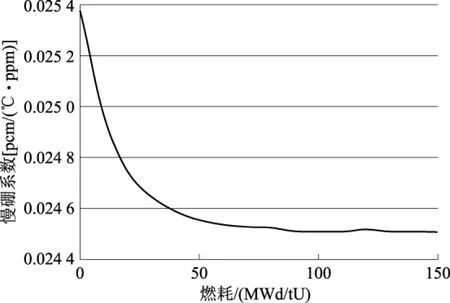
图5 177堆型首循环慢硼系数与燃耗关系Fig.5 The moderator temperature-boron coefficient of 177-assemblies core for different burnup

图6 121堆型首循环慢硼系数与燃耗关系Fig.6 The moderator temperature-boron coefficient of 121-assemblies core for different burnup

由图5、图6可以看出，177和121堆型首循环慢硼系数与燃耗关系曲线的趋势与157堆型的曲线基本一致，得到的慢硼系数均远大于速算公式所给出的CMB(包络)，因而可以采用此速算公式进行计算，得到的结果是保守的。

下面对157堆型不同循环加以计算，得到结果如图7～图9所示结果。

图7 157堆型第二循环慢硼系数与燃耗关系Fig.7 The moderator temperature-boron coefficient of 157-assemblies core second cycle for different burnup

图8 157堆型第三循环慢硼系数与燃耗关系Fig.8 The moderator temperature-boron coefficient of 157-assemblies core third cycle for different burnup

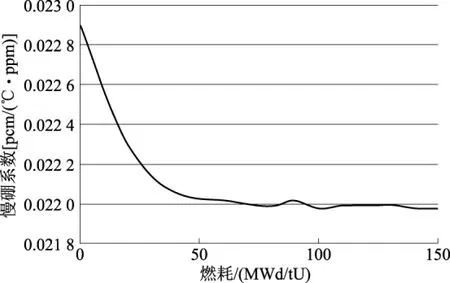
图9 157堆型第四循环慢硼系数与燃耗关系Fig.9 The moderator temperature-boron coefficient of 157-assemblies core forth cycle for different burnup

由图7～图9可以看出，157堆型第2～4循环慢硼系数与燃耗关系曲线的趋势与157堆型首循环基本一致，得到的慢硼系数均远大于速算公式所给出的CMB(包络)，因而可以采用此速算公式进行计算，得到的结果是保守的。

以上分析可知，计算所得的慢硼系数均远大于CMB(包络)=0.02 pcm/(℃·ppm)，可以有效地包络不同堆型以及同一堆型的不同循环。

5 总结

5.1 方法描述

本文通过研究慢化剂温度系数与硼浓度的变化关系，提出慢硼系数(CMB)这一概念，并探究了慢硼系数与功率、燃耗、硼浓度值的关系，得到了慢硼系数的拟合计算公式，并将慢硼系数应用于硼浓度限值计算中，得到计算硼浓度限值的方法。

硼浓度的限值计算公式：

(10)

5.2 详细的修正公式

计算分析得到慢硼系数计算公式如下：

CMB=CMB基准-8.3×10-6ΔBORE+

3.9×10-3ΔP2+4.8×10-3ΔP+

2×10-8ΔBU3+4×10-7ΔBU2-

4×10-5ΔBU

(11)

注：该公式的燃耗适用范围为0～20MWd/tU

福清1号机组基准状态BORE=1182ppm，BU=0，P=0，CMB基准=0.022 534 pcm/(℃·ppm)

5.3 速算公式

为方便工程应用，CMB(包络)=0.02 pcm/(℃·ppm)而得到硼浓度限值速算公式：

BORE限值=BOREnow-50×ΔMTC

(8)

根据此公式，可以快速计算出硼浓度限值，此公式可以在工程上加以应用。

5.4 验证的结论

为验证修正公式的准确性，对给定慢化剂温度系数，利用程序进行硼浓度搜索，修正公式计算的结果与硼浓度搜索得到的结果相近，说明修正公式是正确的；

为验证速算公式的保守性，对给定慢化剂温度系数，利用程序进行硼浓度搜索，速算公式计算的结果小于硼浓度搜索得到的结果，说明速算公式具有保守性；

为验证速算公式的适用性，对不同堆型(121、157堆型)、不同循环(157堆型2、3、4循环)分别加以计算验证，计算所得慢硼系数均大于速算公式所采用的CMB(包络)，说明速算公式的应用具有广泛的适用性。因而本文所给出的速算公式具有实用价值，可以在工程上加以使用。

[1] 核反应堆物理分析，谢仲生，西安交通大学出版社 原子能出版社

[2] 压水堆核电站燃料管理燃料制造与燃料运行，肖岷，原子能出版社

[3] 实验反应堆物理导论，罗璋琳 史永谦 潘泽飞，哈尔滨工程大学出版社

Study of the maximum boron concentration limit for positive moderator temperature coefficient

GAO Xin1, LIU Guo-ming1,CAI Guang-ming2

(1.China Nuclear Power Engineering Co., Ltd, Beijing, 100840, China; 2. Fujian Fuqing Nuclear Power Co., Ltd, Fuqing of Fujian Prov, 350318, China)

The negative moderator temperature coefficient is not only the basis of self-adjusting feature for PWR, but also the safety requirement of PWR design and operation. Within the framework of certain technical specifications, in start-up phase of a low power state, the positive moderator temperature coefficient for the regulation of operation is disadvantageous. Therefore the maximum boron concentration limits must be given to the operating personnel to ensure the moderator temperature coefficient is negative based on the zero-power test results. This paper, through the study of the relationship between moderator temperature coefficient and the concentration of boron, proposed the concept of moderator temperature-boron coefficient and studied the relationship between moderator temperature-boron coefficient and power, burnup, boron concentration, and derived a modified formula of moderator temperature-boron coefficient. Finally, the exactitude formula and the quick calculation formula of the highest boron concentration limits to ensure that the moderator temperature coefficient is negative have been given and their conservative applicability has been verified.

2016-10-29

高 鑫(1985—)，男，吉林白城人，工程师，硕士，现主要从事堆芯物理专业相关工作

TL375.5

A

0258-0918(2017)02-0203-07