探究四川省PM2.5污染的空间分布

甘茂林， 吕王勇,2*， 符 璐

(1. 四川师范大学 数学与软件科学学院, 四川 成都 610066; 2. 可视化计算与虚拟现实四川省重点实验室, 四川 成都 610066)

探究四川省PM2.5污染的空间分布

甘茂林1， 吕王勇1,2*， 符 璐1

(1. 四川师范大学 数学与软件科学学院, 四川 成都 610066; 2. 可视化计算与虚拟现实四川省重点实验室, 四川 成都 610066)

为探究四川省21个市州PM2.5污染的空间分布,有效地利用数据、减少信息损失,将各市州的地理距离与经济变量相关性相结合,构建地理-经济变动空间权重矩阵来刻画各市州之间的相互影响程度,并采用一种改进的Moran’s I 指数分析四川省PM2.5污染的空间分布情况,绘制Moran散点图、局部Moran’s I指数集聚图等将PM2.5污染直观地呈现.结果表明:从整体看,四川省PM2.5污染呈现空间正相关性,高污染地区与高污染地区聚集;从局部看,成都平原城市群、川南城市群和少部分川东北城市群的城市PM2.5污染情况较严重，且呈现空间聚集状态,而在攀西城市群、3个少数民族自治州以及少部分川东北城市群的城市自身的PM2.5污染较轻,但周围城市污染较为严重, 呈现PM2.5污染空间负相关性.

地理-经济变动空间权重矩阵; 改进Moran’s I 指数; 空间自相关; PM2.5

PM2.5是指环境空气中空气动力学当量值≤2.5 μm的颗粒物,也称细颗粒物[1].PM2.5是霾的主要构成成分,是雾霾天气的“罪魁祸首”.PM2.5携带大量的有毒有害物质,对人体的伤害极大.有研究指出,雾霾天气对人体和环境造成的危害与空气中PM2.5的浓度成正相关[2].2012年,我国增设PM2.5平均浓度限值,从此PM2.5进入人们的视线,并且成为大众评价空气质量好坏的一个重要指标.PM2.5在空间分布上往往表现出一定的规律性,根据Tobler的地理学第一定律:所有的地理事物都存在关系,但距离较近的事物比距离较远的事物更有关系[3].对PM2.5空间分布的研究,一般采用空间统计分析方法.而空间自相关是空间统计分析的前提,是认识空间分布特征的方法之一[4].空间自相关能揭示空间变量的结构特征[5],其中Moran’s I指数是其最基本的测度.近年来,国内外学者对空间自相关的研究主要集中在地理空间权重矩阵的构造与选择[4,6]、针对经济问题的经济空间权重矩阵的构造[7-9]、空间关系模型的选择[10-12]及Moran’s I指数的应用与思考[13-15]等.本文提出一种将地理距离与经济变量结合的新的空间权重矩阵,并采用改进的Moran’s I指数计算四川省21个市州PM2.5的空间自相关关系,了解四川省PM2.5污染的空间特征与分布情况.

1 研究方法

空间自相关分析是研究某空间单元与其相邻空间单元之间,就同一属性变量,通过统计方法,计算空间自相关性程度,进而分析这些空间单元在空间上分布现象的特征[16]. 空间自相关分析涉及到空间权重矩阵的构建、空间自相关的度量与检验、空间关联的识别等[17].

1.1 地理-经济变动空间权重矩阵 对于空间权重矩阵,其设定方法有多种,最常用的是采用邻接标准或距离标准来构造空间权重矩阵.邻接标准是指空间单元i与空间单元j的位置关系，若相邻，则设置wij=1 ,否则设置wij=0.邻接标准认为空间关系是否存在只取决于二者是否相接.对于某空间单元的不同邻接空间单元,认为不同邻接空间单元对该空间单元的影响程度是相同的,这在环境污染研究中是不符合客观事实的.距离标准是指空间单元i与空间单元j的相互影响程度与距离有关:距离越近,影响程度越大；反之,则越小.一种常用的空间距离权重矩阵的定义如下:

(1)

其中dij表示空间单元i、j之间的地理距离.wij不仅可以用地理距离刻画,也可采用经济距离刻画.yi、yj表示空间单元i、j的某一经济变量,两者通常具有相似的变化趋势,以yi、yj作为自变量与因变量构建线性回归方程

(2)

将标准残差std(εij)作为元素构造空间经济权重矩阵,即

(3)

若空间单元i与j的该种经济变量相关关系越强,则(2)式的拟合效果越好,其残差的波动范围越小,标准残差std(εij)就越小,导致wij越大；若两地经济变量的相关关系越弱,即两地经济变量的变化趋势不相似,则(2)式的拟合效果越差,残差波动范围越大,标准残差std(εij)就越大,导致wij变小.这种权值设定方法的优点是适应性强,因为随着地区经济的不断发展,各地区间的经济关系是不断变化的,这种随着地区经济关系改变而动态变化的空间权重矩阵能够更好地衡量各地区间的相关关系[7].显然,以标准残差构建的空间权重矩阵不是对称的.

考虑到PM2.5随着空气的流动性和经济发展对PM2.5的影响,本文将地理距离和经济变量共同纳入空间权重矩阵W的设定之中,即

(4)

其中

(5)

dij表示空间单元i、j之间的地理距离,std(εij)表示空间单元i、j经济变量的标准残差.wij越大,表明空间单元i、j之间的相互影响程度越大,关系越紧密;wij越小,表明空间单元i、j之间的相互影响程度越小.对角线元素wii=0,i=1,2,…,n,表示任意一个空间单元都不与自身发生空间关联.该地理-经济变动空间权重矩阵没有简单地考虑两地之间的邻接关系,而是将地理距离作为权值的一个因素,更加符合环境污染的实际情况,也符合Tobler的地理学第一定律.另一方面,地区经济关系的变动在很大程度上带动着环境的变化,加入经济变量的空间权重矩阵能更好地反映各地区间的相关关系.

1.2 空间自相关统计量Moran’s I指数

1.2.1 传统Moran’s I指数 空间自相关统计量有Moran’s I指数、Grary’s C指数、广义G统计量.本文选择使用最广泛、统计意义最明显的Moran’s I指数.全局Moran’s I指数用于分析整个研究区域的空间自相关性,局部Moran’s I指数用于分析每个空间单元与其周围空间单元的自相关性.全局Moran’s I 指数和局部Moran’s I指数的公式[18-19]分别为:

(6)

(7)

1.2.2 改进Moran’s I指数 值得注意的是：xi表示空间单元i的观测值,如1个月或者1个季度、1年获得1个xi.当数据的时间间隔更短时,如1 h、1 d获得1个xi,研究者往往取一段时间数据的均值作为xi,这造成空间单元信息的缺失,降低了最终结果的可信度.因此本文采用1种改进的Moran’s I指数,能更加有效地利用数据、减少信息的损失.

改进全局Moran’s I指数和改进局部Moran’s I指数的公式如下:

(8)

(9)

1.2.3 改进Moran’s I指数与传统Moran’s I指数的关系 为了说明改进Moran’s I指数比传统Moran’s I指数更合理,能更有效地利用数据,减少信息损失,现给出如下2个引理.

引理1 传统全局Moran’s I指数

与改进全局Moran’s I指数

之间的关系为

其中A、B、X、Y都为常数.

证明 对改进全局Moran’s I指数进行变形可得

(10)

(11)

不妨令

则

(12)

(13)

因此,I′和I之间的关系可表示为

(14)

其中A、B、X、Y都为常数,得证.

引理 2 传统局部Moran’s I指数

与改进局部Moran’s I指数

之间的关系为

其中C、D、E都为常数.

(15)

在传统局部Moran’s I指数中,根据

对传统局部Moran’s I指数进行变形得

(16)

不妨令

则

(17)

(18)

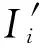
(19)

其中C、D、E均为常数,得证.

引理1和引理2表明,改进全局Moran’s I指数、改进局部Moran’s I指数比传统全局Moran’s I指数、传统局部Moran’s I指数包含了更多的数据信息,更加有效地利用数据,这与改进Moran’s I指数的初衷一致.

1.2.4 Moran’s I指数的显著性检验 根据L. F. Lee[20]的矩阵算法推导出改进全局Moran’s I指数的期望与方差为：

(20)

Var(I′)=

(21)

其中,

同理,根据L. F. Lee[20]的矩阵算法推导改进局部Moran’s I指数的期望与方差为：

(22)

(23)

其中,

得到改进Moran’s I指数的期望、方差后,对Moran’s I指数进行显著性检验,以确定造成此种关系是因为存在空间分布还是偶然因素.构造Z检验统计量

(24)

在α=0.05的显著性水平下,若Z介于-1.96～1.96之间,表明在所研究的空间范围内某现象分布的关联性不明显,空间自相关性较弱;若Z在(-1.96,1.96)之外,表明在所研究的空间范围内某现象的分布具有显著的相关性,空间相关性较强.

2 实证分析

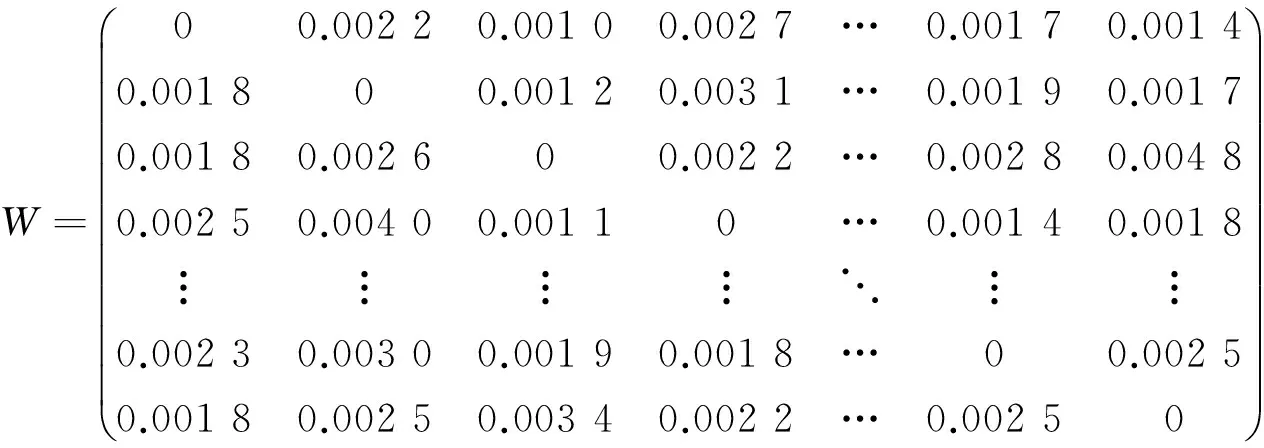
2.1 数据预处理 本文从PM2.5历史数据网站[21]搜集整理2015年1月1日至2015年9月30日四川省21个市州PM2.5的日平均浓度数据,欲探求四川省PM2.5空间分布情况.根据本文定义的地理-经济变动空间权重矩阵,以各市州的市政府间的地理距离表示dij;以各市州2000年—2014年GDP数据拟合方程的标准残差表示std(εij).根据(5)式构建地理-经济变动空间权重矩阵并对该空间权重矩阵进行全局归一化，得到归一化的地理-经济变动空间权重矩阵

(25)

(25)式中的非零元素表示四川省两地之间的关联程度：数值越大,两地的相关性越大,相互影响程度越大;数值越小,两地的相关性越小,相互影响程度越小.对角线上的0元素表示各地市均不与自身发生自相关.在该地理-经济变动空间权重矩阵中,除0元素外,w2,19的值最小,为0.000 725,表示自贡与阿坝州的相关性最小,两地的相互影响程度最小;w6,5的值最大,为0.006 36,表示绵阳与德阳的相关性最大,两地的相互影响程度大.

2.2 空间自相关指标分析 根据改进全局Moran’s I指数(8)式和传统全局Moran’s I指数(6)式,计算四川省21个市州改进全局Moran’s I指数和传统全局Moran’s I指数,并分别对其进行显著性检验.表1为四川省PM2.5污染的全局Moran’s I指数.

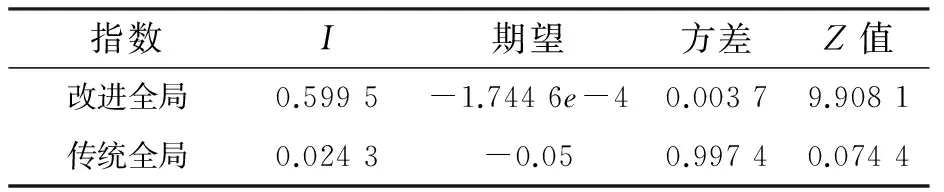
表 1 四川省PM2.5污染改进全局Moran’s I指数指数与传统全局Moran’s I指数

由表1可知,传统全局Moran’s I指数为0.024 3,其Z值处于(-1.96,1.96)之内,表明传统全局Moran’s I指数未能探测出显著空间正相性.

改进全局Moran’s I指数为0.599 5,表明四川省PM2.5污染的空间分布具有正相关性,在地理分布上呈现出集聚现象,其分布并不是处于完全的随机状态,而是受各市州PM2.5污染的影响.根据Z值为9.908 1，可以判断四川省PM2.5污染的聚集状态是显著的,这是的确存在的空间分布而不是偶然因素造成的.四川省PM2.5整体呈现空间聚集现象,但不能保证每个市州的PM2.5污染都是空间聚集,也不能保证每个市州的空间状态是显著的.因此，每个市州的空间自相关性还需通过局部Moran’s I指数做进一步判断.表2是四川省21个市州的局部Moran’s I指数及对应的Z值.

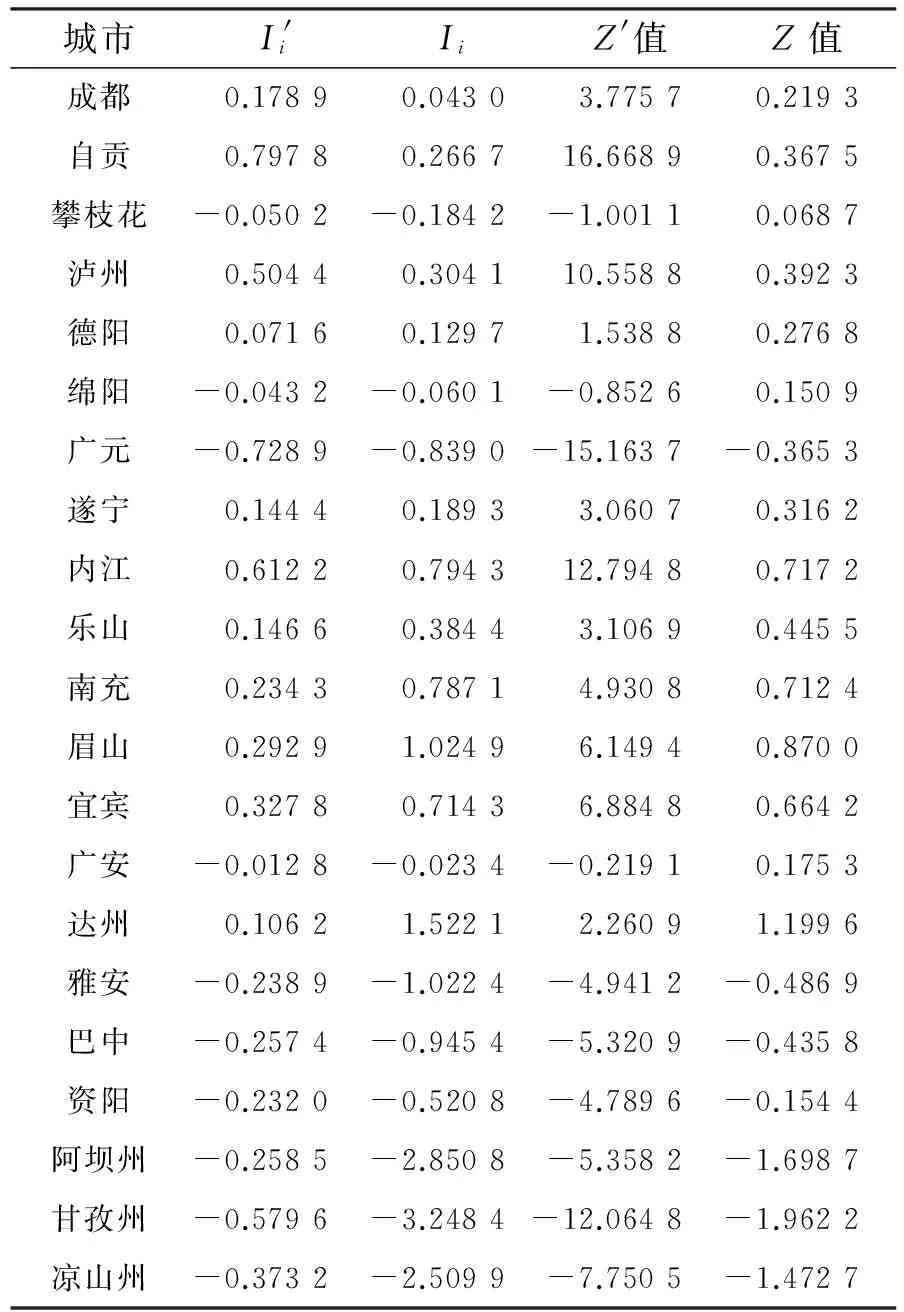
表 2 四川省PM2.5污染改进局部Moran’s I指数与传统局部Moran’s I指数及Z值

以标准化PM2.5数据x*为横坐标,nWx*为纵坐标绘制Moran散点图.图1为四川省PM2.5污染的Moran 散点图.结果显示,所有的点只分布在第一、二象限,其中成都、眉山等11个城市的PM2.5污染表现出高-高(H-H)的正相关关系集群,即高污染地区被高污染的其他地区所包围;广元、甘孜州等10个城市的PM2.5污染表现出低-高(L-H) 的负相关关系集群,即低污染地区被高污染的其他地区所包围.

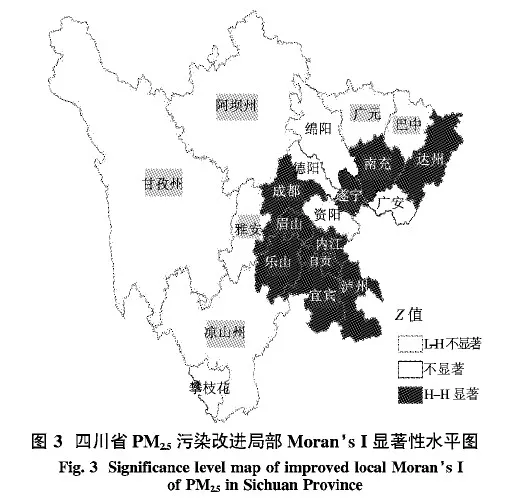
为了更好地分析污染的空间分布情况,本文使用ArcMap 10.2软件将四川省PM2.5污染分布情况可视化.图2为四川省PM2.5污染改进局部Moran’s I集聚图.图3为四川省PM2.5污染改进局部Moran’s I显著性水平图.由图2可得,四川省PM2.5污染的空间分布规律非常明显,四川盆地中心地带的成都平原城市群,位于长江上游、川滇黔渝交界处的川南城市群和少部分川东北城市群的城市[22]的局部Moran’s I指数大于0,呈现PM2.5空间聚集分布.结合图1可以得出这些城市处于H-H区域,其PM2.5污染情况较严重,呈现污染严重区域与污染严重区域的聚集,以川南城市群尤为突出.通过图3显著性水平图可以看出川南城市群的聚集不是偶然出现的,而是由某一系统过程造成的.位于第一象限除德阳外的眉山、自贡等10个城市均通过5%的显著性检验，成为PM2.5污染排放H- H显著集聚中心.而在四川盆地边缘地带的攀西城市群、3个少数民族自治州以及少部分川东北城市群大多处于低污染被高污染围绕的状态,即这些城市自身的PM2.5污染较轻但周围城市污染较为严重,呈现PM2.5污染空间负相关性.广元和甘孜州的PM2.5污染与周围城市的空间负相关性最大.位于第二象限除绵阳、广安、攀枝花外的广元、雅安等7个城市均通过5%的显著性检验成为PM2.5污染排放L-H显著集聚中心.

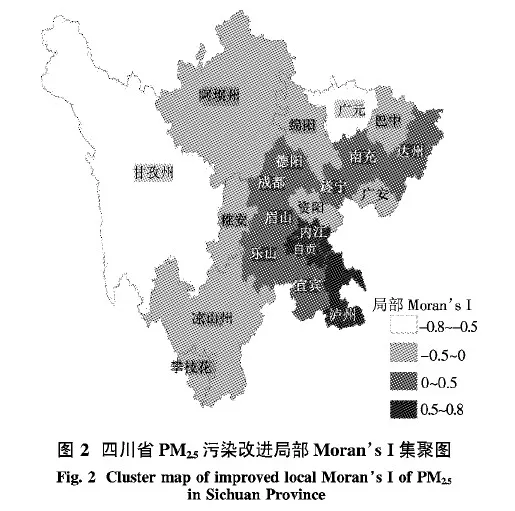
通过改进全局Moran’s I指数与改进局部Moran’s I指数比较分析,可以得出四川省PM2.5污染分布高值聚集占主导地位,整体呈现空间聚集分布,在不同的市州PM2.5的分布情况又有不同.PM2.5污染呈现这样的空间分布的原因大概包括以下几个方面:第一,由于地理距离较近,以成都为中心的城市群在成都经济的高速发展下各自也发展迅速,人口的增多、工业的快速发展,导致成都平原城市群PM2.5高值显著聚集.第二,川南城市群位于长江上游四川南部,川滇黔渝三省一市的交界处,幅员面积约4.42 万km2,也是四川省域内人口稠密的地区之一.该城市群拥有较强的工业基础和特色优势产业,是成渝两地经济能量交换的区域,因此川南城市群PM2.5污染的空间正相关性最强.第三,川东北城市群是连接省内外的交通要塞、重要的经济腹地.近年来,随着达成铁路、成南高速公路、广南高速公路、达渝高速公路的建成通车,带动了遂宁、南充、达州的交流和发展,增加了城市之间的相互影响,因此空间正相关性较强,而广元、巴中两市与秦岭山脉相邻,常年多风,因此PM2.5污染较轻.第四,攀西城市群与少数民族自治州的自然环境优美、旅游业发达,环境保护力度强,因此成为PM2.5污染较轻、空间负相关性强的地区.

3 结论

本文利用空间自相关分析对四川省21个市州的PM2.5污染的空间分布进行探究.考虑到经济对于城市关系的影响,采用一种地理与经济结合的动态空间权重矩阵刻画21个市州之间的相互影响程度.这种空间权重矩阵不仅包含了基于地理距离的影响还包含地区间经济发展的相关关系,更为深刻地刻画了地区之间的相互影响程度,体现了地区关系的丰富内涵.

由于传统Moran’s I指数对于数据的利用不够有效,本文采用一种改进Moran’s I指数,它更能挖掘空间数据之间的自相关关系.通过这种动态空间权重矩阵和改进Moran’s I指数的计算分析,得出如下结论:

1) 从整体区域看,四川省PM2.5污染具有显著空间聚集分布,呈现空间正相关性.

2) 从局部看,四川省PM2.5污染的空间分布规律比较明显,成都平原城市群、川南城市群和少部分川东北城市群的城市PM2.5污染情况较严重,呈现污染严重区域与污染严重区域的聚集.在攀西城市群、3个少数民族自治州以及少部分川东北城市群自身的PM2.5污染较轻但周围城市污染较为严重,呈现PM2.5污染空间负相关性.

3) PM2.5的空间自相关性与城市的经济、地理位置、周围城市的影响、交通等多方面因素存在一定的关系.

[1] 国家质量监督检验检疫总局. 环境空气质量标准G3095—2012[S]. 北京：中国环境科学出版社,2012.

[2] 吴兑. 灰霾天气的形成与演化[J]. 环境科学与技术,2011,34(3):157- 161.

[3] TOBLER W. On the first law of geography:a reply[J]. Ann Assoc Am Geo,2004,94(2):304-310.

[4] 王红亮,胡伟平,吴驰. 空间权重矩阵对空间自相关的影响分析:以湖南省城乡收入差距为例[J]. 华南师范大学学报(自然科学版),2010,42(1):110-115.

[5] 曾辉,江子瀛,孔宁宁,等. 快速城市化景观格局的空间自相关特征分析：以深圳市龙华地区为例[J]. 北京大学学报(自然科学版),2000,36(6):824-831.

[6] 任英华,游万海. 一种新的空间权重矩阵选择方法[J]. 统计研究,2013,29(6):99-105.

[7] 王君婕,张宁. 新的空间权重矩阵在中国碳排放分析中的应用[J]. 中国商贸,2014(31):206-208.

[8] 张嘉为,陈曦,汪寿阳. 新的空问权重矩阵及其在中国省域对外贸易中的应用[J]. 系统工程理论与实践,2009,29(11):84-92.

[9] 李婧,谭清美,白俊红. 中国区域创新生产的空间计量分析:基于静态与动态空间面板模型的实证研究[J]. 管理世界,2010(7):43-55.

[10] 吴贤荣,张俊飚,程琳琳，等. 中国省域农业碳减排潜力及其空间关联特征：基于空间权重矩阵的空间Durbin模型[J]. 中国人口资源与环境,2015,25(6):53-61.

[11] CHENG T, WANG J Q, HAWORTH J, et al. A dynamic spatial weight matrix and localized space-time autoregressive integrated moving average for network modeling[J]. Geographical Analysis,2014,14(1):75-97.

[12] AHRENS A, BHATTACHARJEE A. Two-step lasso estimation of the spatial weights matrix[J]. Econometrics,2015,3(1):128-155.

[13] 欧变玲,龙志和,林光平. 图解Bootstrap 方法用于空间相关性Moran 检验的有效性[J]. 统计与信息论坛,2011,26(2):3-8.

[14] 代侦勇,姜婧,肖明科. 基于时空Moran’s I指数的全国降雨量自相关分析[J]. 华中师范大学学报(自然科学版),2014,48(6):923-929.

[15] 冯文兰,牛晓俊. 快速城市化地区建设用地的空问特征与演变分析：以成都市为例[J]. 四川师范大学学报(自然科学版),2015,38(4):576-583.

[16] 陈慈仁,林峰田,何燦群. 空间自相关聚集分析[EB/OL]. (2014-12-17)[2015-11-1]. http://www.docin.com/p-993166513.html.

[17] 罗畏,邹峥嵘. 空间统计分析的环境质量评价应用[J]. 测绘科学,2012,37(4):32-37.

[18] CLIFF A D, ORD J K. Spatial Processes[M]. London:Pion,1981:266.

[19] ANSELIN L. Local indicators of spatial association[J].Geographical Analysis,1995,27(2):93-115.

[20] LEE L F. GMM and 2SLS estimation of mixed regressive, spatial autoregressive models [J]. J Econometrics,2007,137(2):489-514.

[21] 王杰. PM2.5历史数据[DB/OL]. (2016-9-27)[2015-11-1]. http://www.aqistudy.cn/historydata/.

[22] 四川省统计局. 四川省四大城市群经济实力研究[EB/OL]. (2014-1-8)[2015-11-1]. http://www.sc.gov.cn/10462/10464/10465/10574/2014/1/8/10290302.shtml.

[23] 杨春,余江,余毅,等. 成都市PM2.5指标的影响因子分析及其防治策略[J]. 西南民族大学学报(自然科学版)2016,42(6):626-630.

2010 MSC：62P12

(编辑 陶志宁)

Exploring the Spatial Distribution of PM2.5in Sichuan Province

GAN Maolin1, LYU Wangyong1,2, FU Lu1

(1.CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan；2.VisualComputingandVirtualRealityKeyLaboratoryofSichuanProvince,Chengdu610066,Sichuan)

To explore the spatial distribution of PM2.5in 21 cities in Sichuan Province, in order to use data effectively and reduce information damage, we combine the geographical distance of the cities and the correlation of economic variables to structure the geography-economic dynamic spatial weight matrix that describes the interaction. We analyze the spatial distribution of PM2.5in Sichuan Province by using an improved Moran’s I and drawing scatter diagram of Moran, cluster map of local Moran’s I, et al, to present the spatial distribution of PM2.5. The results show that the pollution of PM2.5has a positive correlation in Sichuan Province on the whole, and highly polluted area are clustered. From the local perspective, pollution of PM2.5of cities in Chengdu city-group, chuannan city-group and a few chuandongbei city-group are serious and the pollution shows spatial aggregation. But cities in panxi city-group, 3 ethnic autonomous prefectures and a few chuandongbei city-group are slightly polluted where pollution is more serious in surrounding urban. These cities show negative correlation of PM2.5pollution.

geography-economic dynamic spatial weight matrix; improved Moran’s I; spatial autocorrelation; PM2.5

2015-11-13

国家自然科学青年基金(11601357)、四川省教育厅自然科学重点项目(15ZA0030)和可视化计算与虚拟现实四川省重点实验室项目(KJ201410)

X821

A

1001-8395(2017)01-0029-09

10.3969/j.issn.1001-8395.2017.01.005

*通信作者简介：吕王勇(1979—),女,副教授,主要从事数理统计与数据分析的研究,E-mail:lvwangy@163.com