盾构施工对某邻近既有隧道的影响分析
张 芳,潘 浩
(安徽建筑大学 土木工程学院,安徽 合肥 230601)
盾构施工对某邻近既有隧道的影响分析
张 芳,潘 浩
(安徽建筑大学 土木工程学院,安徽 合肥 230601)
地下地铁的建设已成为缓解城市地面交通拥堵问题的重要途径,但随着城市地下地铁建设的发展,往往会遇到盾构施工毗邻或交叉某些既有隧道等问题。笔者采用数值模拟和监测数据分析的方法对合肥地铁南站5号线下穿1号线时,1号线的拱顶沉降、管片受力、管片变形进行分析,并将两种方法获得的结果进行对比分析,从对比分析中找出二者的异同,总结规律,为施工正常进行提供理论的指导,也为类似工程提供相应参考。
盾构施工;交叉隧道;数值模拟;现场监测;对比分析
随着经济发展更加快速,人口数量急剧增加,城市已经拥挤不堪,城市空间利用迫在眉睫,为了解决这一重大问题,发展城市地下交通是解决这一问题的关键所在。
现今,合肥城市地下交通有8条线路,其中,有2个三线交叉换乘车站,18个2线交叉换乘车站,这种隧道与隧道之间的交叉施工特别复杂,要考虑的因素也多,这种交叉方式大致分为二种,第一种是地下相交隧道的两个空间的交叉,第二种是新建隧道与既有隧道的交叉,这种相互交叉隧道的施工在工程中尤为特殊,因此隧道交叉的相互影响分析研究与实际工程的结合是非常重要的。
目前,国内外有关隧道交叉相互影响分析的研究已经有了大量的研究课题和研究成果。孙钧、刘洪洲等[1]利用软件建立三维弹塑性有限元模型,分析了交叠隧道土层位移及地表沉降曲面在盾构推进中的发展变化。杨兆辉、郭晨等[2-7]通过结合工程实例,对邻近的交叉隧道进行了数值模拟与分析,通过比较不同施工工艺与不同地质条件,如:应力场,管片应力,地表位移与变形等几大特点,通过模拟邻近的交叉施工过程,分析工程特点,总结规律。
1 工程概况
合肥南站5号线下穿1号线的工程概况里有2标段区间工程,其中包括有1号线隧道右线长621.384 m,隧道左线长616.788 m;5号线隧道右线长473.175 m,隧道左线长462.344 m。1号线与5号线的位置关系为斜交且1号线左线与5号线的左右线斜交而右线无交集,5号线左线下穿1号线左线,两条隧道竖向距离约为3.276 m,即两隧道间土层厚度为3.276 m,5号线右线下穿1号线左线,两条隧道竖向距离约为4.26 m,即两隧道间土层厚度为4.26 m。
隧道的开挖方式是从繁华大道开始,盾构区间为繁~高区间,之后盾构驶入高铁南站内部,然后完成调头、过站,接着穿过高铁南站下方的桩基群和合宁高速公路,最后在高铁南站的南广场下方下穿1号线左线。
1号线的左右线区间间距约为15.2~41.5 m,且左右线分别有两个标段的曲线段,半径均为350 m,5号线的左右线区间间距约为9~12.95 m,且左右线仅有一个标段的曲线段,右线半径为365 m,左线半径为380 m。
高铁站~繁华大道站区间内,1号线左、右线最小坡度为2‰,最大坡度为22.4‰,区间隧道距离上部地表埋深约8.8~22.1 m。高铁站~繁华大道站区间内,5号线左、右线最小坡度为11‰,最大坡度为28.5‰,区间隧道距离上部地表埋深约11.9~28.4 m。
上部覆土依次为:人工杂填土、粘土(膨胀土)、粘土(膨胀土)、粘土、全风化粉砂岩、强风化粉砂岩。有关地层地质的参数如表1所示。
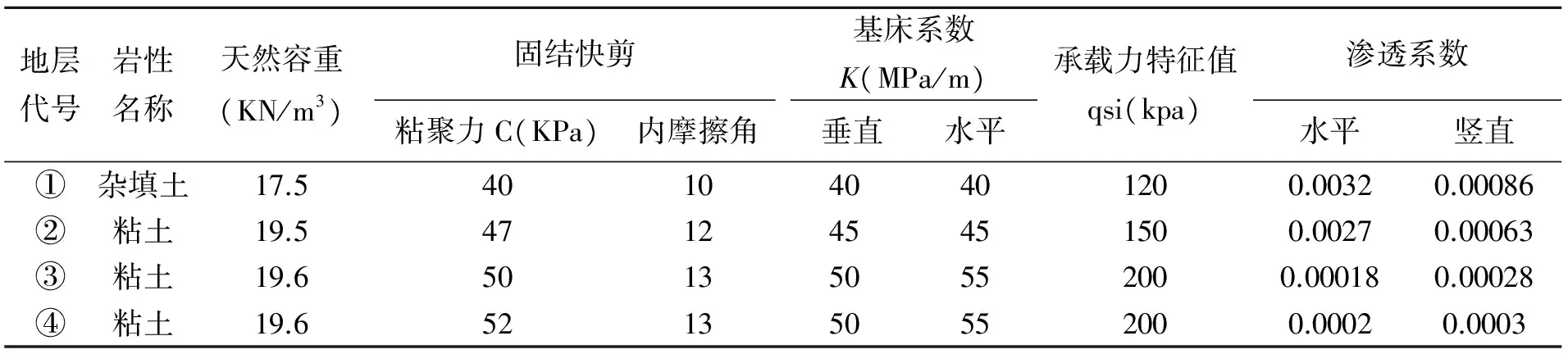
表1 地层地质参数表
数据来源:笔者整理。
2 数值模拟
2.1 三维数值模型的建立过程
三维数值模型的建立过程主要是通过有限元分析软件Midas GTS NX对合肥地铁5号线下穿1号线左线的工程实例进行模拟竖向空间交叉时,1号线的变形及受力情况以及盾构区间上方地表沉降变化的规律。实际工程工况中上下交叉隧道的距离为3m,现以盾构隧道与既有隧道垂直距离的不同为工况,研究不同距离盾构施工时对既有的1号线的影响分析,然后与实际的盾构隧道引起的变化做对比分析。
根据实际的施工地质条件及施工工况,利用有限元分析软件建立数值分析模型,其相应的参数如下:模型大小为110*130*50,上部覆土厚度依次为1.5 m、3.5 m、28 m、7 m、10 m,1号线隧道顶部距离上部土层厚度为8.8 m,5号线拱顶距离1号线拱顶距离为3 m,距离上部土层距离为17 m,盾构隧道半径为3 m,衬砌的厚度为0.3 m,距离左右边界的距离约为18 m。
2.2 模型图的建立
根据上述实际工况的地质条件,不改变其他参数的前提下,我们将盾构隧道5号线向上平移至与上部隧道距离为2 m的情况为工况一,将实际相符的工况作为工况二,而将盾构隧道5号线向下平移至与上部隧道距离为5 m的情况为工况三。各隧道空间位置云图以及各工况数值模拟隧道布置图分别如图1和图2所示。(各工况数值模拟隧道布置图相近这里不重复出图)
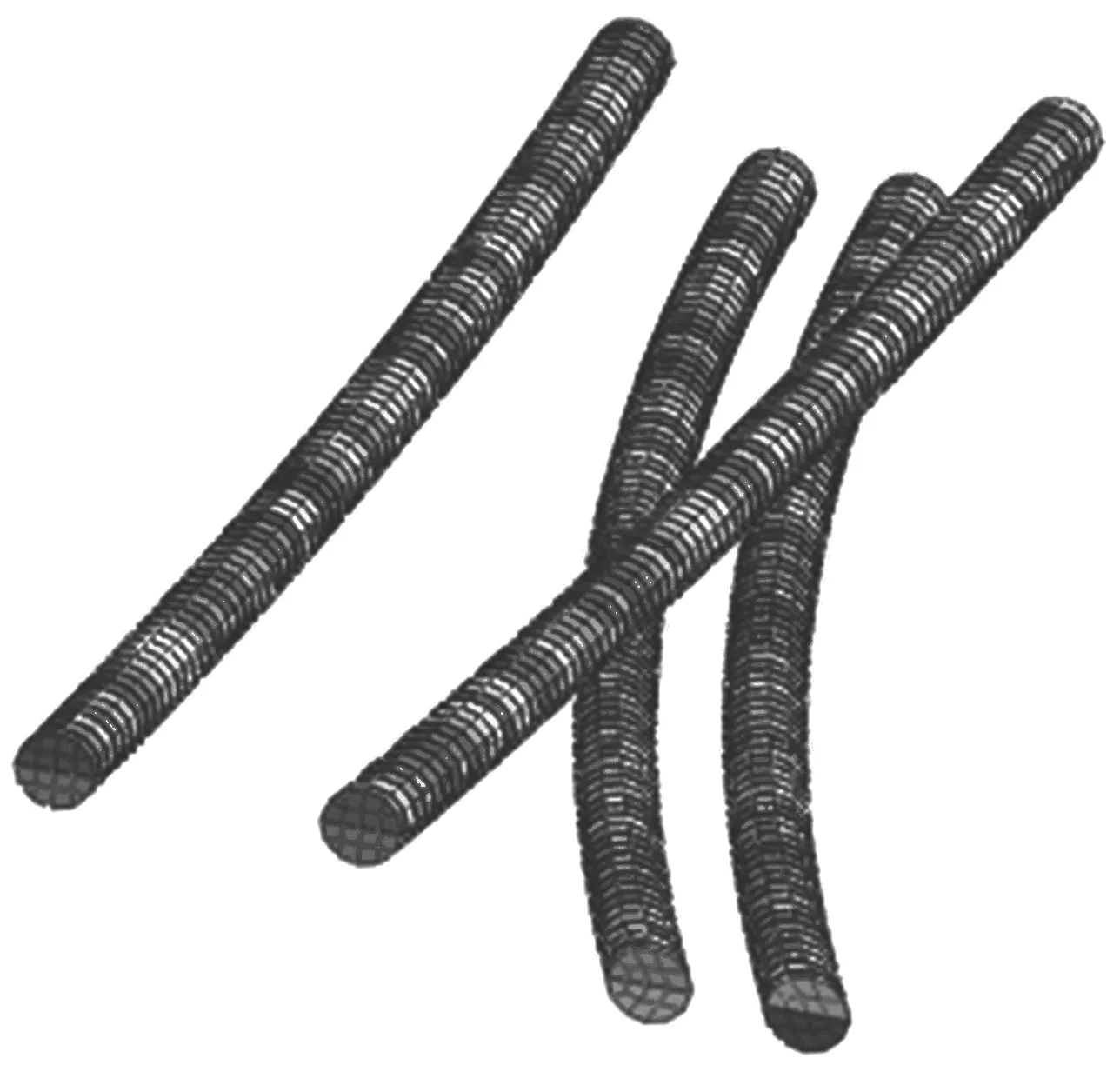
图1 各隧道空间位置云图

图2 各工况模型图
3 模拟数据与实测数据对比分析
3.1 不同工况下数值模拟结果的沉降与应力分析
我们整理三种工况的拱顶的沉降与管片受力可以得到三种工况的对比分析图分别如图3和图4所示。
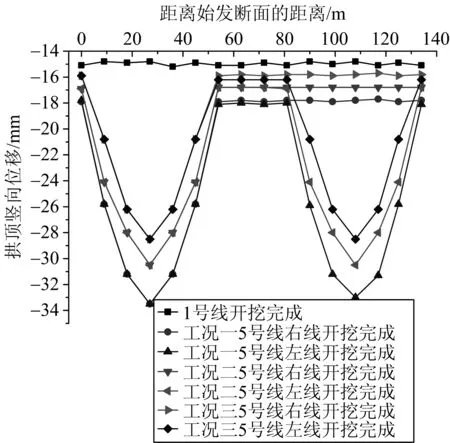
图3 三种不同工况下1号线拱顶沉降变化曲线图

图4 三种不同工况下1号线管片受力变化曲线图
我们通过改变5号线下穿1号线的垂直竖向距离来定义不同的工况,且三种不同工况中有相似的地方也有不同的地方,相同的地方表现在1号线开挖完成的情况在三种工况下拱顶的沉降变化与管片应力变化是相同的,而下穿的盾构隧道则由距离的不同盾构时对上部1号线左线的影响程度就不同,但数值模型的建立大致相同,通过对比总结,可得出以下结论:
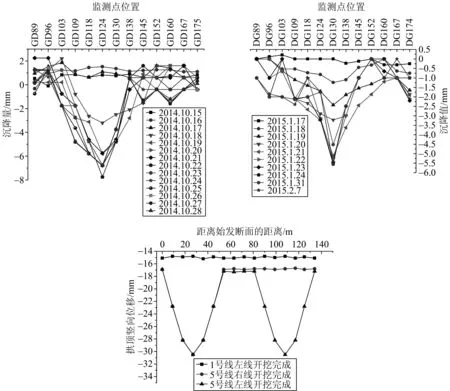
图5 实测与模拟结果拱顶沉降对比图
(1)随着距离始发断面的距离越远,盾构施工5号线右线在推进过程中,在0~30 m范围内,1号线左线拱顶沉降在逐渐加大,这也是盾构即将到达两隧道的交叉点位置,之后拱顶沉降达到最大值30 mm,盾构掘进到达交叉点位置,也是施工影响对既有隧道影响最大的危险点处。随着盾构施工的推进,盾构远离交叉点,拱顶沉降开始慢慢变小,最后沉降值稳定在17 mm左右,这比1号线开挖完成后的沉降又下降了2 mm,这也能看出远离交叉点的位置越远,拱顶沉降影响越小。
(2)三种工况下施工对1号线左线的影响非常相似,5号线右线的开挖随着距离交叉点位置的逼近拱顶沉降与应力均在增大,而随着距离交叉点位置的远离又在减小,之后远离到一点距离的其他点的数值无明显沉降。5号线左线的开挖类似5号线右线开挖的过程,但5号线左线与1号线交叉点位置到5号线右线与1号线交叉位置间的拱顶沉降与应力变化都受到5号线左线盾构开挖的影响。
3.2 拱顶位移变化的对比
我们对实测的1号线左线的拱顶沉降变化与模拟的5号线盾构时1号线左线的拱顶沉降变化做对比分析,可得对比图,如图5所示。
通过图5实测结果与数值模拟结果对比我们可以得出如下几点结论:
(1)数值模拟的结果大致上与实际所测数据反应的一致,最大沉降位置点、拱顶各测点沉降趋势、5号线左右线顺序开挖后1号线拱顶沉降的变化特征等方面基本相符,但我们发现在对比图中一些沉降值大小有出入,这主要是5号线盾构时所测数据为1号线沉降清零的基础上监测的,但总体相符。
(2)实测数据图中是一个历时的变化曲线图,而数值模拟的图形是最终的沉降图,实测数据由于在数据的采集、处理、整合的过程难免会有遗漏或者填写错误,进而导致位移图散点、图起点、弯折点比较多整体凌乱,但仍能较清晰的客观反映该拱顶沉降的规律。数值模拟的曲线图中的数据来之软件,数据比较全,比较规律因此图形比较工整,但模拟是扔忽略了一些软件没有办法的考虑的因素,所得图形也稍有瑕疵,但整体与实测数据能有对应起来。
3.3 管片应力变化的对比
将实测的1号线左线的拱顶沉降变化与模拟的5号线盾构时1号线左线的管片应力变化做对比分析,可得对比图如图6所示。

图6 实测与模拟结果管片应力变化对比图
通过图6实测结果与数值模拟结果对比我们可以得出如下几点结论:
(1)数值模拟的结果大致上与实际所测数据反应的一致,最大应力位置点、应力在各测点变化趋势、5号线左右线顺序开挖后1号线管片应力的变化特征等方面基本相符,但我们发现在对比图中一些应力值大小有出入,这主要是5号线盾构时所测数据为1号线应力清零的基础上监测的,但总体相符。
(2)实测数据图中是一个历时的变化曲线图,而数值模拟的图形是最终的沉降图,实测数据由于在数据的采集、处理、整合的过程难免会有遗漏或者填写错误,进而导致位移图散点、图起点、弯折点比较多整体凌乱,但仍能较清晰的客观反映该1号线左线管片受力的规律。数值模拟的曲线图中的数据来之软件,数据比较全,比较规律因此图形比较工整,但模拟是扔忽略了一些软件没有办法的考虑的因素,所得图形也稍有瑕疵,但整体与实测数据能有对应起来。
4 结论
本文就合肥南站地下交叉隧道工程实例为背景,利用有限元模拟软件分析了合肥地铁5号线左右线盾构开挖对1号线的影响分析,总体从盾构交叉隧道的位移量与管片受力上进行分析,通过数值模拟分析并结合实测数据对比研究,得出变化量图形以及对比分析数据图,从图形及实测数据可以得到如下结论:
(1)对于5号线左右线下穿1号线时,1号线拱顶的沉降变化基本稳定,5号线右线盾构开挖时,1号线拱顶竖向沉降最大值为7.55 mm,而后沉降稳定值在6.755 mm附近,最大隆起部分数值在2.3 mm左右,而5号线左线盾构开挖时,1号线拱顶沉降与沉降值变化量明显比右线盾构开挖时的变化值要小,工程中可针对拱顶沉降问题对每个隧道盾构时的情况进行处理。
(2)管片受力分析中,左右线开挖时管片应力值差别较大,右线开挖时,管片受力最大值达到23.18 kN,且两者均发生了管片受力突变量都超出了预警值,实际工程中发现管片小部位破损,并有渗水,较多管片有小部位破损、开裂、错台,施工中应及时做好相应补救措施确保工程安全推进。
(3)通过数值模拟工况的对比分析以及实际工程中的监测数据与软件模拟实际工况下所得数据的比较,我们发现有限元软件在很大程度上可以反映实际施工的情况,这样我们可以利用软件模拟对实际施工进行理论指导,分析工程中的危险位置,提前防范,确保工程安全。
[1]孙钧,刘洪洲.交叠隧道盾构法施工土体变形的三维数值模拟[J].同济大学学报,2002(4):379-385.
[2]张庆贺,朱忠隆,杨俊龙,等.盾构推进引起土体扰动理论分析及试验研究[J].岩石力学与工程学报,1999(6):699-703.
[3]何川,苏宗贤,曾东洋.盾构隧道施工对已建平行隧道变形和附加内力的影响研究[J].岩石力学与工程学报,2007(26):2064-2065.
[4]张志强,何川.地铁盾构隧道近接桩基的施工力学行为研究[J].铁道学报,2003(1):91-95.
[5]李哲,张子新.相邻隧道施工对上海地铁二号线的影响分析[J].岩石力学与工程学报,2005(24):5126-5128.
[6]巫环主.支线交叉重叠段隧道施工技术总结[J].西部探矿工程,2005(111):210-212.
[7]Chehade F H, Shahrour I. Numerical Analysis of the Interaction between Twin-tunnels: Influence of the Relative Position and Construction Procedure[J].Tunneling and Underground Space Technology,2008,23(2):210-214.
Research on the Shield Tunneling Exerts Influenceson a Nearby Existing Tunnel
ZHANG Fang, PAN Hao
(SchoolofCivilEngineering,AnhuiJianzhuUniversity,Hefei230601,China)
The construction of underground subway has become an important way to alleviate the problem of urban ground traffic congestion. However, with the development of urban underground subway construction, the shield construction adjacent to or crossing some existing tunnel is always occurred. In this paper, the method of numerical simulation and analysis of the monitoring data have been adopted to make an analysis the line 1 of the vault settlement, the stress of segment, the deformation of segment for the Hefei Subway Station line 5 crossing line 1. The results obtained by the two methods were compared and analyzed, and find out the similarities and differences between the two methods from the comparative analysis. Final summary of the law not only provides theoretical guidance for the construction of the normal, but also provides a corresponding reference for the similar projects.
shield construction; crossing tunnel; numerical simulation; on-site monitoring; comparative analysis
2017-03-13
张芳(1993-),女,安徽合肥人,硕士研究生,研究方向:道路与桥梁工程理论与运用;潘浩(1990-),男,安徽亳州人,硕士研究生,研究方向:地下结构计算理论与应用。
U45
A
1009-9735(2017)02-0133-05

