无轴承交替极永磁电机悬浮绕组及其特性研究

丁 强,邓智泉,王晓琳

(1.南京航空航天大学,南京210016;2.南京工业职业技术学院,南京210023)

0 引 言

在同一定子内集成电机与磁轴承功能的无轴承电机技术,在航空航天、医药化工、半导体技术等领域有其应用特色[1-4]。无轴承永磁电机因为高功率密度、高效率的优势颇受关注[5-7]。然而,传统无轴承永磁电机存在诸如高磁阻永磁体增加悬浮功耗、转矩和悬浮力性能无法兼顾、悬浮控制依赖转子位置信息等不足之处。

针对表贴式无轴承永磁电机存在的问题,交替极转子无轴承永磁电机得到关注[8]。该电机悬浮磁通经过低磁阻铁磁材料闭合,悬浮功耗低,可同时兼顾转矩和悬浮力性能。此外,当转子极对数大于等于4时,悬浮控制与转子位置信息无关。

文献[8]在忽略悬浮磁势空间高次谐波的条件下,研究分布式悬浮绕组无轴承交替极永磁电机悬浮力模型与极对数的关系;文献[9]分析3种定子结构对多极对数无轴承交替极永磁电机悬浮性能的影响;文献[10]在“C”型定子结构上,实现同极式转子和交替极转子相结合的双层转子无轴承交替极永磁电机;文献[11]对双层转子无轴承交替极永磁电机的附加轴向永磁体对悬浮和转矩特性影响展开研究;文献[12]研究一种带被动磁轴承的外转子交替极无轴承永磁电机并通过优化永磁体磁极形状提高电机的起动性能;文献[13]通过增加定子齿宽降低饱和效应对悬浮性能的影响。

目前,无轴承交替极永磁电机本体结构一直是研究热点[14-15]。但是,现有研究是在特定绕组结构下,优化定、转子结构改善悬浮性能,而忽略绕组结构本身对悬浮性能的影响。

悬浮绕组结构影响悬浮磁势分布和空间谐波含量,本文从计及悬浮磁势空间谐波的悬浮力模型出发,定义悬浮力/电流刚度、悬浮力脉动率、径向最大耦合度等3个悬浮性能参数的基础上,在同一定、转子结构上,通过改变悬浮绕组结构,研究悬浮性能的变化规律。最后,对不同悬浮绕组下悬浮性能进行定性对比,为无轴承交替极永磁电机悬浮系统设计提供参考。

1 电机结构及工作原理

本文针对定子12齿、转子4对极的交替极无轴承永磁电机展开研究,如图1所示。从悬浮机理和绕组结构出发,研究悬浮绕组结构对悬浮特性的影响,所得结论适用于不同齿极数组合的无轴承交替极永磁电机。

图1 无轴承交替极永磁电机截面图

图1 以产生正x方向径向力说明悬浮机理,4块S极面向气隙的永磁体的永磁磁通为虚线所示,1对极悬浮磁通为粗黑实线。由于永磁体磁阻大于转子铁极,悬浮磁通经由铁极磁路闭合。可以看出,右侧气隙内永磁磁通和悬浮磁通相互叠加、左侧气隙磁密永磁磁通和悬浮磁通相互减弱。左、右侧气隙磁密的不平衡产生x正方向悬浮力。

同理,注入y方向悬浮电流将产生y方向悬浮力。需要说明的是,由于悬浮磁通总是通过铁极形成闭合回路,使得径向力与转子转角无关。

2 悬浮力表达式及性能指标

本文在计及悬浮磁势空间谐波情况下,推导悬浮力表达式,推导过程以产生x方向悬浮力为例,并做如下假设:

1)转子位于定子中心;

2)仅考虑转子铁极下悬浮力;

3)忽略磁饱和;

4)气隙磁通方向沿径向。

定子气隙磁势A(φs)分布可表示:

式中:Ap,Asx(φs)分别为永磁磁势和悬浮磁势。

假定悬浮磁势为方波,其傅里叶变换可表示:

式中:n为奇数次空间谐波磁势;an为悬浮磁势各次谐波有效值。

根据气隙磁势可得气隙磁密B(φs)表达式:

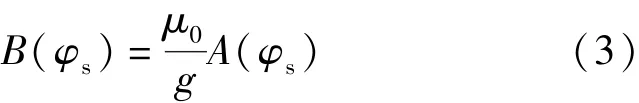
式中:μ0为真空磁导率;g表示气隙长度。

根据气隙磁密可以得到径向力x轴分量Fx及y轴分量Fxy:

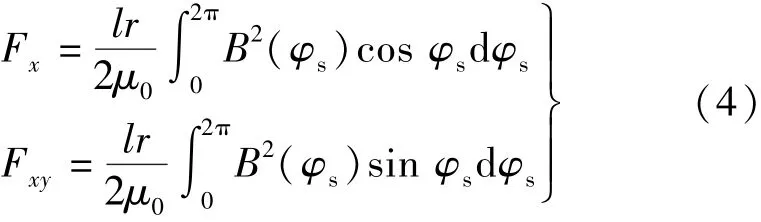
式中:l,r分别表示电机轴向长度、平均气隙半径。将式(1)～式(3)代入式(4)可得:

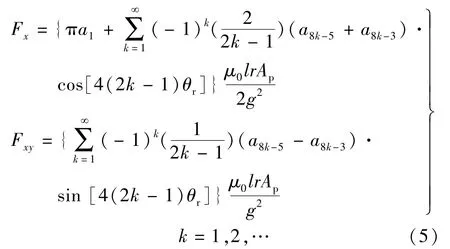
式中:a1,a8k-5,a8k-3分别为悬浮磁势基波以及空间谐波系数;θr表示转子位置角。

从式(5)看出,悬浮磁势基波影响悬浮电流利用率,悬浮磁势空间谐波导致悬浮力脉动和径向自由度耦合。同时,悬浮力脉动引起噪声振动、增加悬浮功耗,径向自由度耦合降低系统稳定域[13]。

为定量分析悬浮磁势基波和空间谐波对悬浮特性影响,定义悬浮力/电流刚度fs、脉动率fr和径向最大耦合度fc这3个参数评价无轴承交替极永磁电机悬浮特性。

式中:Fmax,Fmin和Fav表示一个电周期悬浮力最大值、最小值和平均值。文献[9]指出fr和fc均小于10%时,可提高悬浮精度、系统稳定性及降低功耗。

鉴于悬浮磁势空间谐波造成悬浮力脉动及径向自由度耦合,首先对悬浮绕组结构、磁势分布和空间谐波进行研究。

3 悬浮绕组及其磁势

由式(5)可知,悬浮磁势空间谐波影响悬浮特性。考虑到磁势空间谐波与绕组结构有关,本节首先对集中式和分布式两种基本悬浮绕组结构展开研究。在此基础上,从减小绕组端部和降低磁势空间谐波角度,进一步根据磁势等效原则和磁势总谐波畸变最小原则分别研究环形式悬浮绕组和带辅助线圈的集中式悬浮绕组。每种绕组结构分别研究两相和三相形式,重点分析悬浮磁势空间谐波含量及分布。

3.1 集中式悬浮绕组

图2是集中式悬浮绕组结构(记为Wc)。图2(a)为两相集中式悬浮绕组,Nx,Ny分别代表x和y方向绕组线圈。图2(b)为三相集中式悬浮绕组,三相绕组轴线空间互差120°电角度(Ni(i=u,v,w)代表i相线圈)。

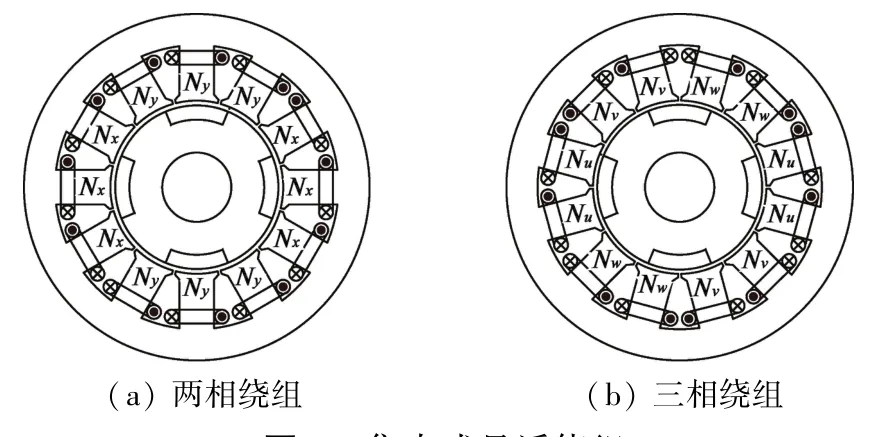
图2 集中式悬浮绕组

两种悬浮绕组在正x方向悬浮电流时磁势如图3所示(下文相同),其中FI(FI=N·I)为每个线圈的安匝数。

图3 集中式绕组悬浮磁势

对悬浮磁势进行傅里叶分解,并以(2/π)NI为基值归一化(下文相同),如图4所示。

图4 集中式绕组悬浮磁势空间谐波

由图4可知,绕组铜耗相同时,三相悬浮磁势大于两相悬浮磁势,三相悬浮磁势基波幅值大于两相绕组形式。由式(5)知,三相绕组的悬浮力/电流刚度大于两相绕组。此外,三相悬浮绕组不包含3次及其倍数次谐波,三相悬浮绕组磁势总谐波畸变(以下简称THD)小于两相悬浮绕组。

3.2 分布式悬浮绕组

图5是分布式悬浮绕组(记为Wd)。图5(a)的两相绕组轴线相互垂直(Nx和Ny分别代表x和y方向绕组线圈),每相绕组由两个短距线圈和一个整距线圈组成。图5(b)的三相绕组轴线互差120°电角度(Ni(i=u,v,w)代表i相绕组圈),两个短距线圈串联成一相绕组。

图5 分布式悬浮绕组

图6 为两种悬浮绕组磁势分布。对比图3和图6发现,分布式悬浮绕组磁势更接近正弦,磁势空间谐波含量低于集中式绕组,因此,分布式绕组的悬浮性能优于集中式悬浮绕组。

图6 分布式绕组悬浮磁势分布

对分布式悬浮绕组磁势空间谐波进行分析,如图7所示。相同线圈安匝数时,三相悬浮绕组磁势空间基波幅值大于两相悬浮绕组,三相绕组具有更高的悬浮力/电流刚度。同时,三相悬浮绕组不包含3及3倍数次空间谐波,三相悬浮绕组磁势总谐波畸变低于两相悬浮绕组。对比图4和图7,分布式悬浮绕组磁势基波要大于集中式悬浮绕组,因此,分布式绕组悬浮电流利用率高于集中式绕组。

图7 分布式悬浮磁势空间谐波

3.3 环形式悬浮绕组

本文依据悬浮磁势等效原则,用集中式线圈构造如图8所示的环形式悬浮绕组(记为Wt)等效分布式悬浮绕组。一般而言,集中式线圈端部小于分布式线圈,因此,环形式悬浮绕组具有端部小的优势。

图8(a)的两相环形式悬浮绕组,Nx,Ny分别代表x,y方向绕组线圈。图8(b)的三相环形式悬浮绕组,三相绕组轴线互差120°电角度(Ni(i=u,v,w)代表i相线圈)。

图8 环形式悬浮绕组

图9 是悬浮磁势单独作用且分布式绕组和环形式绕组线圈安匝数相同时气隙径向磁密对比。可以看出,环形式悬浮绕组与分布式悬浮绕组气隙径向磁密分布几乎相同,因此,两种悬浮绕组磁势等效关系成立。对环形式悬浮绕组磁势及空间谐波分析可参照图6和图7。

图9 分布式与环形式绕组气隙磁密对比

3.4 带辅助线圈的集中式悬浮绕组

环形式悬浮绕组仅对分布式悬浮绕组磁势进行等效,而磁势空间谐波没有降低。为进一步降低磁势空间谐波,同时不增加端部长度,在集中式悬浮绕组基础上,通过引入辅助线圈,构造分布效应,改变集中式悬浮绕组磁势空间分布。

图10为通过引入集中式辅助线圈(Nia(i=x,y,u,v,w)为辅助线圈)构造的带辅助线圈的集中式悬浮绕组结构(记为Wca)。辅助线圈配置在对应主绕

图10 带辅助线圈的集中式悬浮绕组

组线圈组相邻齿上,辅助线圈与主绕组线圈匝数配比关系:

式中:M为主绕组线圈匝数;Ma为辅助线圈匝数;k在区间[0,1]取值。控制绕组系数k,可改变磁势分布,降低空间谐波。

图11为绕组的悬浮磁势分布。

图11 带辅助线圈的集中式绕组悬浮磁势分布

对图11进行傅里叶分析,两相和三相绕组悬浮磁势总谐波畸变表达式:

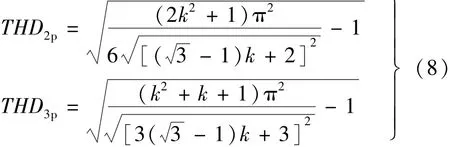
本文提出以悬浮磁势THD最小为优化目标,确定绕组系数k,此时,两相和三相的绕组系数分别为0.549和0.366。在此基础上得到悬浮磁势空间谐波分布,如图12所示。三相悬浮绕组磁势基波幅值大于两相悬浮绕组;优化后的绕组系数k使三相悬浮绕组除11,13及23次等高次谐波外,其他谐波均为而两相悬浮绕组各次谐波谐波也得到抑制。

图12 带辅助线圈的集中式悬浮磁势空间谐波

图13 为4种悬浮绕组磁势基波幅值的对比。在线圈安匝数相同时,分布式和环形式悬浮绕组磁势基波幅最大,而带辅助线圈的集中式悬浮绕组磁势基波幅值大于集中式悬浮绕组。

图13 不同绕组磁势基波幅值对比

表1为4种悬浮绕组磁势总谐波畸变对比。集中式悬浮绕组THD高于其他3种绕组形式;分布式悬浮绕组与环形式悬浮绕组具有相同THD值;带辅助线圈的集中式悬浮绕组磁势THD值较小。

表1 悬浮磁势总谐波畸变对比

4 悬浮特性比较

根据上述悬浮绕组结构及磁势空间谐波分析,本节在一台无轴承交替极永磁电机上(具体参数见表2),对悬浮力/电流刚度、悬浮力脉动率和径向最大耦合度等悬浮特性定量研究。

表2 电机主要尺寸

悬浮力/电流刚度是衡量悬浮电流利用率的重要指标。同一类型悬浮绕组,假设两相和三相的铜耗相等,图14为4种绕组悬浮力/电流刚度对比。每种绕组三相结构悬浮力/电流刚度大于两相结构,分布式绕组与环形式绕组悬浮力/电流刚度近似相等且为最大,集中式绕组悬浮力/电流刚度最小,带辅助线圈的集中式绕组居中。对比图13和图14可知,悬浮力/电流刚度由悬浮磁势基波决定。

图14 悬浮力/电流刚度对比

图15 ～图19是4种悬浮绕组一个电周期内(机械角度90°)悬浮力波形。结合式(2)可计算悬浮力脉动率和径向最大耦合度,结果如表3所示。

表3 悬浮力脉动率和径向最大耦合度对比

图15为集中式悬浮绕组一个电周期的悬浮力波形。

图15 集中式绕组悬浮力波形

由表3可知,三相绕组悬浮力脉动率21.8%,径向最大耦合度26.6%,均不满足要求。两相绕组径向力脉动率和最大耦合度分别为4.5%和50.8%,绕组的综合性能较差。

图16为分布式绕组一个电周期的悬浮力波形。

图16 分布式绕组悬浮力波形

由表3可以看出,三相绕组脉动率6.5%,径向最大耦合度8.8%,均满足要求。两相绕组7.9%的径向最大耦合度满足要求,但14.5%的脉动率不满足要求。因此,三相分布式绕组悬浮性能优于两相分布式绕组。此外,分布式绕组悬浮性能要优于集中式绕组。

图17为环形式绕组悬浮力一个电周期的波形。

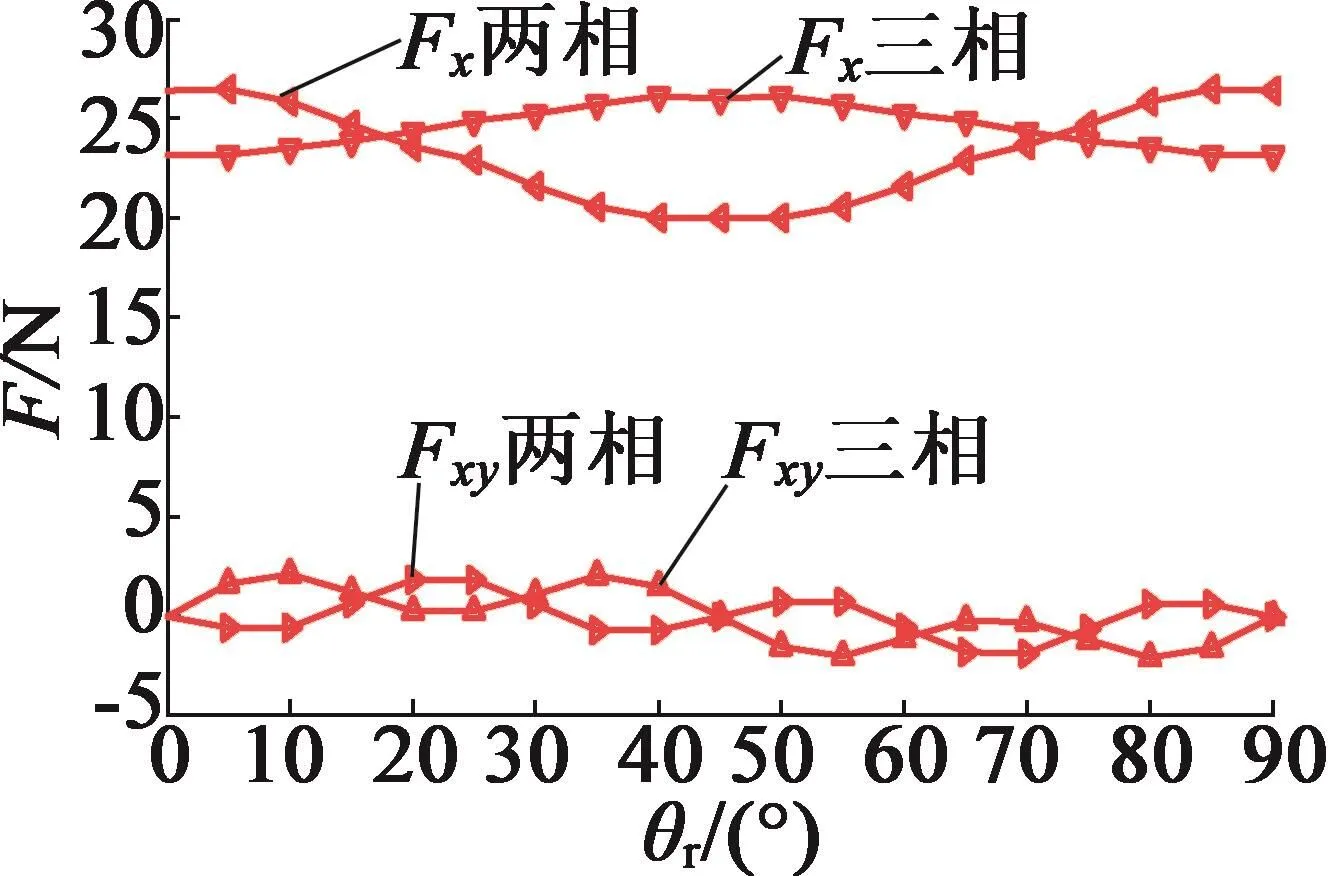
图17 环形式绕组悬浮力波形

由图16和图17可得分布式绕组和环形式绕组一个电周期悬浮力误差波形,如图18所示。一个电周期内两种绕组悬浮力误差较小,悬浮力波形几乎相同。结合表3悬浮力脉动率和径向最大耦合度可知,环形式悬浮绕组与分布式悬浮绕组具有相同的悬浮特性。因此,三相环形式悬浮绕组满足悬浮性能的要求。

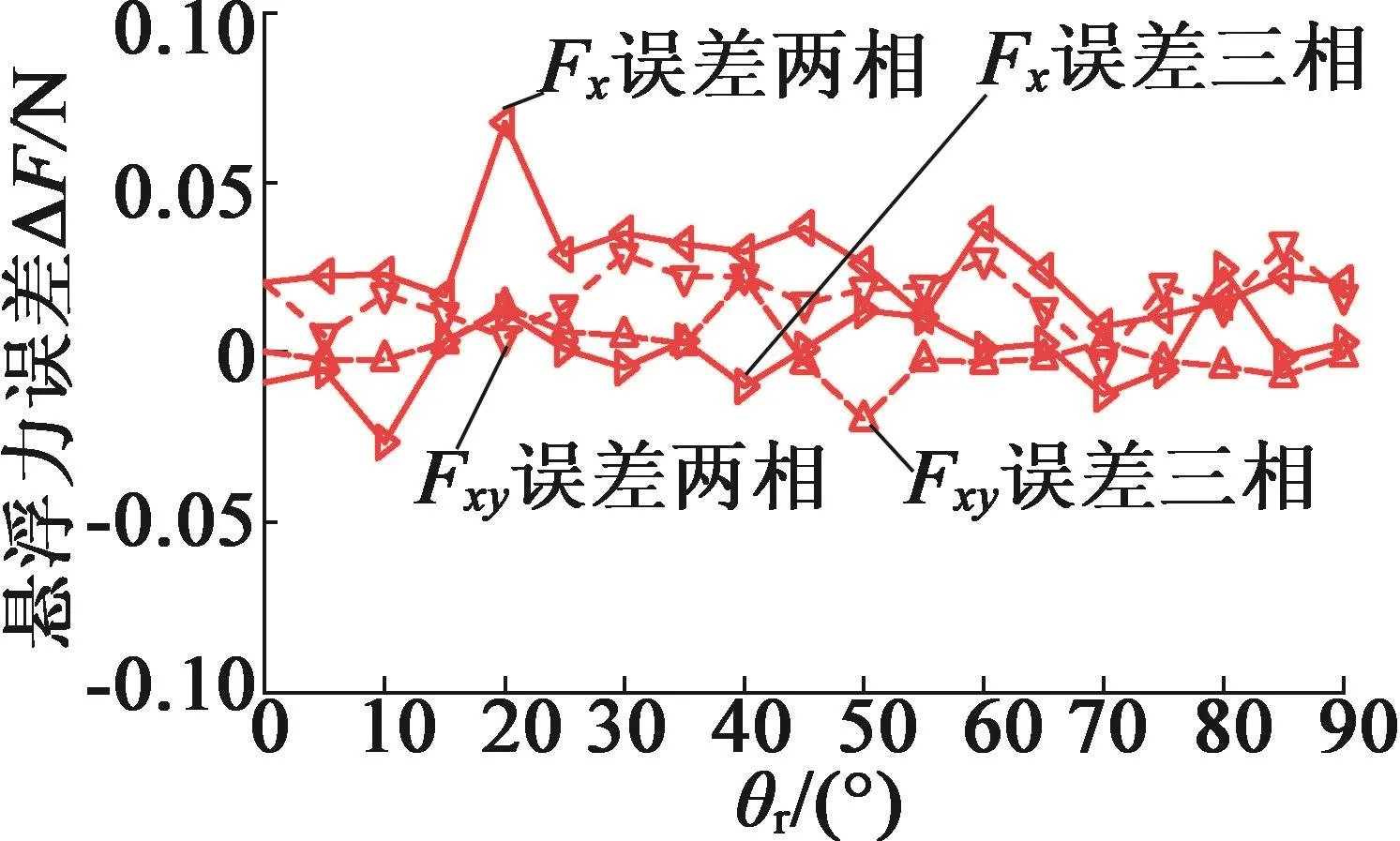
图18 分布式与环形式绕组悬浮力误差波形

图19 为带辅助线圈的集中式绕组悬浮力一个电周期的波形。

图19 带辅助线圈的集中式绕组悬浮力波形

由表3可以看出,两相绕组脉动率为6.3%,径向最大耦合度为7.1%,均满足性能要求。三相绕组的脉动率降至1%,径向最大耦合度被降至4.6%,均满足性能要求。可见,引入辅助线圈并优化绕组系数k,有利于提高悬浮性能。

结合悬浮力/电流刚度、悬浮力脉动率和径向最大耦合度来看,三相悬浮绕组优于两相悬浮绕组。考虑到高悬浮力输出能力和低悬浮系统功耗是无轴承电机悬浮系统基本要求,有必要在铜耗相等条件下,对比4种三相悬浮绕组悬浮力输出能力。

图20是以三相分布式悬浮绕组为基值的悬浮力输出能力对比结果。

图20 悬浮力输出能力对比

从图20可知,绕组铜耗相等时,分布式绕组产生的悬浮力最大,集中式绕组产生的悬浮力最小,为基值的47%;环形式和带辅助线圈集中式绕组产生的悬浮力介于分布式和集中式之间,分别为基值的70.5%和49.5%。因此,相对于分布式绕组,集中线圈形式的绕组悬浮力输出能力弱。

图21为三相悬浮绕组的fr,fc及磁势总谐波含量对比。fr和fc随悬浮磁势空间谐波的增加相应增加。

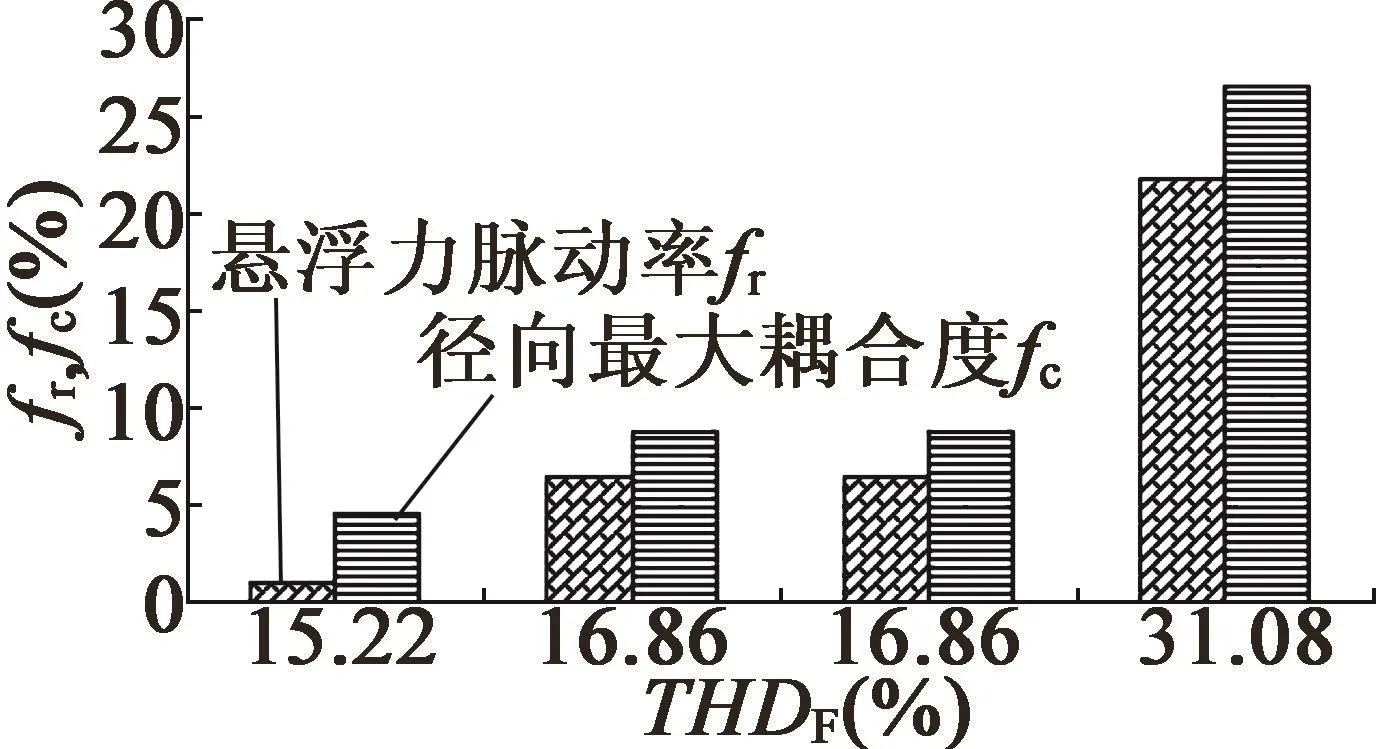
图21 脉动率、径向最大耦合度与悬浮磁势THD关系

综合上述分析,表4对4种悬浮绕组的fs,fr,fc及径向力输出能力定性对比。

表4 不同绕组特性定性对比

其中“优”表示高于平均水平,“良”表示平均水平,“中”表示低于平均水平。

5 结 语

无轴承交替极永磁电机悬浮性能受悬浮绕组及其确定的磁势空间谐波的影响。本文在12齿4对极交替极无轴承永磁电机上,研究了集中式悬浮绕组、分布式悬浮绕组、环形式悬浮绕组以及带辅助线圈的集中式悬浮绕组等4种绕组的悬浮磁势的空间谐波特性对悬浮性能的影响。研究表明,三相形式的悬浮绕组结构总是优于两相悬浮绕组形式;分布式悬浮绕组和环形式悬浮绕组具有较高的悬浮电流利用率;带辅助线圈的集中式悬浮绕组的悬浮力脉动率和径向最大耦合度较小;集中式悬浮绕组悬浮力脉动和径向耦合度较高。