Tornambe非线性鲁棒控制器在异步电动机DTC中的应用
李 阳,任一峰,汲德明
(中北大学,太原030051)
0 引 言
直接转矩控制(以下简称DTC)是德国学者M.Depenbrock和日本学者 I.Takahashi于20世纪80年代中期首先提出的,它以转矩为被控制量进行直接控制,是继矢量控制后的另一种交流调速传动控制方法。由DTC具有控制结构简明、对电机参数依赖小等优点,使得它在众多的交流调速技术中脱颖而出,成为异步电动机调速领域中的一种关键的控制方法。
传统的异步电动机直接转矩控制采用双闭环控制结构,但是一组优化参数只在一定调速范围内具有良好的控制效果,使得高低速区域不能兼顾,系统的稳定性、动态性和控制精度会下降。为了得到较好的控制效果,许多学者在后续研究中不断对调节器进行改进,如文献[1]中用模糊控制调节器代替PI调节器,使低转速情况下稳定精度提高,但是响应快速性无法保证。文献[2]利用量子遗传算法的自适应搜索能力对BP神经网络的初始权值进行优化,防止了局部极小值情况的发生,通过两者的结合实时调节Kp,Ki,Kd这3个基准值,从而克服了控制系统响应速度慢,超调量大的问题,但此方法使速度调节器复杂化,将无法开展实际应用。文献[3]设计神经元控制器代替传统速度调节器,改善了系统的低速动态性能,但也存在和文献[2]中同样的问题。文献[4]将自抗扰控制器应用在调速系统中,虽然避免了经典PI调节器中的某些缺陷,改善系统整体的控制性能,但控制器本身所需整定的参数较多,使得该控制器无法进行深入推广。
Tornambe控制理论是意大利学者A.Tornambe在解决复杂电网控制中提出的一种新的控制理论,在这一理论基础上设计的Tornambe非线性鲁棒控制器(以下简称TNRC)结构简单,控制性能优越并具有较强的鲁棒性,对于参数变化范围宽,大干扰的非线性系统来说十分适用。其理论成果在陀螺稳定平台[5]、无人机[6]、多容水箱[7]和机器人[8-10]等方面已有相关研究。本文用TNRC代替传统DTC中的转速调节器,通过Simulink环境下搭建的仿真模型对系统性能进行分析。结果表明,应用TNRC的异步电动机DTC系统动态性好、鲁棒性强,电磁转矩脉动得到明显改善,且低转速时的稳定精度显著提高。
1 Tornambe非线性鲁棒控制原理
Tornambe控制的主要思想是通过内部的积分环节来补偿系统的各种未知因素,如内外部扰动、参数的不确定性等。TNRC设计的关键是构造出合适的扩张状态观测器对扰动进行估计和补偿,通过输出变量来构造观测器并观测系统扩张状态变量,并将各种未知扰动通过积分环节进行补偿。
对于单输入单输出仿射非线性系统:

式中:x代表系统的状态矢量;y代表系统的输出矢量;f(x),g(x)表示系统模型中的确定性部分;Δf(x),Δg(x)表示系统模型中的不确定性部分,且f(x),g(x),Δf(x),Δg(x)∈CP(Rn,Rn),h∈CP(Rn),其中P为一个正整数,n代表状态向量的维数;f(x),g(x)在其区间内P次可微。
对系统做如下假设[10-12]:
(1)假设系统在某平衡点处的相对阶数r有界且已知。
(2)输出量的各阶倒数均可测。
根据微分几何理论,可构造r个变换坐标函数zi=φi(x)=Li-1fh(x),(i=1,2,…,r),以及n-r个辅助变换坐标函数wi-r=φi(x),(i=r+1,…,n),进一步将系统化为标准型:

式中:a(z,w),Δa(z,w),b(z,w),Δb(z,w)及c(z,w)可由f(x),g(x),h(x)和微分同胚变换函数得到。
进一步假设上述标准化系统满足零动态渐进稳定,且b(z,w)总为正或总为负,则系统的动力学方程可由h0y+h1y(1)+…+hr-1y(r-1)+y(r)=h0r来表示。hi(i=0,1,…,r-1)为使系统稳定选取的闭环极点应位于s的左半平面。
系统的扩张状态定义:
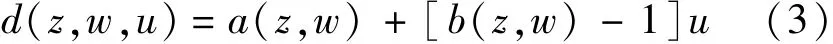
那么,标准化后的系统的动态性能方程可用·z=r d(z,w,u)+u来表示。如果系统的状态变量函数a(z,w)和b(z,w)能够观测,则采用精确反馈线性化方法将d(z,w,u)抵消,实现系统线性化并得到控制律:

但是在实际情况中,由于内、外扰的作用,常常无法获得状态变量a(z,w)和b(z,w)的精确值或使得状态变量a(z,w)和b(z,w)完全未知,这种情况下,便会使系统的控制性能降低。为了消除和补偿系统内部和外部的不确定因素,将用系统扩张状态估计值代替式(4)中的d,则TNRC控制器设计如下:

式中:ki(i=0,1…,r-2)为任意常数,但对系统稳定性起主要作用的是kr-1,所以实际应用中取ki(i=0,1,…,r-2)=0;ξ为计算中产生的中间变量。根据文献[11],用Lyapunov第二稳定性判据可证明当μ>μ*>0时系统是稳定的。
2 基于TNRC的异步电动机DTC
DTC是以空间矢量作为分析工具,通过对定子磁场定向进而对定子磁链和电磁转矩进行直接控制。图1给出了基于TNRC的异步电动机DTC系统原理框图。

图1 系统框图
在图1中,将TNRC作为异步电动机DTC系统中的速度调节器,对转速进行控制,取代传统的PI控制器。该控制系统为一个一阶模型,但由于一阶TNRC在动态性和稳定性上都比二阶TNRC差,所以设计二阶TNRC。其中以转速n为被控制量,根据式(5)设计方程如下:

根据式(6)构建的二阶控制器,其结构如图2所示。
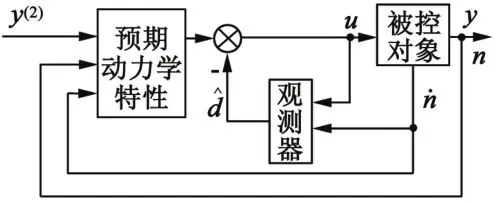
图2 控制器结构
从图1可知,系统是将检测到的三相定子电压、电流值转变为两相值,将其输入到定子磁链转矩观测器中,经过计算输出磁链实际值ψs、转矩实际值Te和磁链在静止的α-β坐标系下的磁链分量ψsα和ψsβ,将给定转速n*与输出的转速n通过TNRC调节得到转矩给定值T*e,并与实际转矩值Te相减得到的转矩误差,经过转矩调节器得到转矩开关信号Tq。 磁链给定值|ψ*s|与磁链实际值ψs相减得到磁链误差,通过磁链调节器得到磁链的开关信号ψq。将转矩开关信号、磁链的开关信号和通过磁链区间判断得到的开关信号N通过开关表进行开关选择,从而对逆变器进行控制,进而实现电机的可靠运行[11]。
3 仿真结果
基于TNRC的异步电动机DTC系统仿真模型如图3所示。
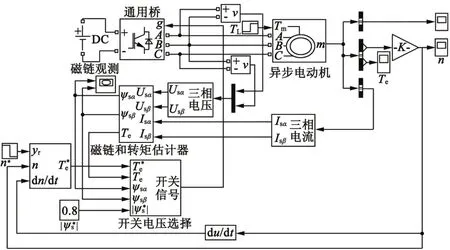
图3 仿真模型
选取的电机参数如下:额定电压Us=380 V,额定频率f=50 Hz,额定功率Pn=1.5 kW,定子电阻Rs=1.85 Ω,转子电阻Rr=1.16 Ω,定子电感Ls=0.519 2 H,转子电感Lr=0.519 2 H,定转子间的互感为Lm=0.489 3 H,转动惯量为J=0.004 88 kg·m2,极对数p=4。在仿真时间为0.4 s时负载转矩由0增加为15 N·m,转速在仿真时间为0.7 s时由初始的1 400 r/min下降为200 r/min。在Simulink界面中,对传统异步电动机DTC和基于TNRC的异步电动机DTC进行仿真,并对比分析。为保证良好的控制效果,利用优化函数对两种控制系统的控制器参数分别进行参数整定。图4为传统异步电动机DTC的仿真结果。
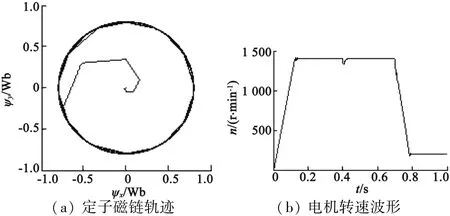

图4 基于PI控制器的异步电动机DTC仿真结果
图5 为在相同条件下,基于TNRC的异步电动机DTC的仿真结果。

图5 基于TNRC的异步电动机DTC仿真
从仿真结果来看,当电机处于高速运行时,基于TNRC的异步电动机DTC对整个系统响应迅速,且响应曲线平滑,无超调;当突加负载时,能够迅速追踪给定转速;且在低速运行条件下,磁链轨迹未发生明显畸变,定子电流也能快速恢复成稳定的正弦曲线;在0.4 s和0.7 s系统状态发生改变的情况下,基于TNRC的异步电动机DTC系统较传统异步电动机DTC系统,其抗干扰能力和快速响应能力明显增强。
4 结 语
根据Tornambe非线性鲁棒控制理论设计TNRC,并将其引入到异步电动机 DTC中。通过Simulink环境下建模仿真的结果可知,用TNRC取代传统PI控制器后,系统动态变化情形下,仍然对输出量取得一种高效的控制效果,其快速响应能力和抗干扰能力也明显增强,且很好地改善了异步电动机低速情形下的运行特性,增强了控制系统整体的动态性和控制精度,验证了TNRC的有效性。通过将Tornambe控制技术应用到异步电动机控制领域,为今后得到一种新型控制器奠定了理论基础。
[1]李鸿彪,曼苏乐.一种改进的异步电机无速度传感器.直接转矩控制系统[J].电气自动化,2012,34(4):13-15.
[2]彭继慎,宋朋磊.改进PID和模糊控制在异步电机DTC.中的应用[J].计算机仿真,2014,31(6):329-333.
[3]李莺,蒋泽甫.基于神经元和直接转矩控制技术的高性能交流调速系统研究[J].重庆邮电大学学报,2010,22(1):118-121.
[4]吴其洲.DRNN-ADRC异步电机直接转矩控制系统研究[J].控制工程,2011,18(3):335-337,368.
[5]左哲,李东海.陀螺稳定平台状态补偿控制[J].航空学报,2008,29(1):141-148.
[6]李之果,陈亚锋.无人直升机非线性鲁棒控制器设计及仿真[J].现代电子技术,2015,38(13):98-100.
[7]张云帆,李东海,老大中.多容水箱的TC控制[A].第24届中国控制与决策会议论文集[C]//太原,2012:3604-3609.
[8]NICOSIA S,TORNAMBE A.Experimental results in state estimation of industrial robots[C]//Proceedings of the 29th IEEE Conference on Decision and Control.USA:IEEE,1990:360-365.
[9]NICOSIA S,TORNAMBE A.Experimental validation of asymptotic observers for robotic manipulators[C]//Proceedings 1990 IEEE International Conference on Roboticsand Automation.USA:IEEE,1990:1423-1430.
[10]TORNAMBE A.Global regulation of a planar robot arm striking a surface[J].Automatic Control,IEEE Transactions on Automatic Control(S0018-9286),1996,41(10):1517-1521.
[11]TORNAMBE A.A decentralized controller for the robust stabilization of a class ofMIMO dynamical systems[J].Journalof Dynamic Systems.Measurement and control(S0022-04 34),1994,116(2):293-304.
[12]李娜.Tornambe控制技术研究及应用[D].太原:中北大学,2014.

