起重机用永磁电机等效热阻法瞬态温度场计算
韩雪岩,于占洋,李生祥
(沈阳工业大学,沈阳110870)
0 引 言
起重机用永磁电机整体呈细长型特殊结构,长细比可达20,使得铜损耗过大,所以起重机用细长型永磁电机温升计算尤为重要。通过有限元仿真可以进行精确计算温升,但该方法对计算机配置有着较高要求,而且其建模和仿真过程耗费大量时间。为此,本文针对起重机用细长型永磁电机提出瞬态等效热网络模型,对电机瞬态温度场进行计算分析。
目前,永磁电机瞬态温度场计算的方法主要有3种:等效热网络法、有限差分法以及有限元法。其中,等效热网络法主要用于电机稳态温度场计算,对于电机瞬态温度场计算研究较少[1-4]。同济大学何磊等人针对电动汽车的驱动电机,基于等效热网络法求取永磁电机温度场的瞬态变化特性,并验证该模型具备较高的可靠性[5]。文献[6]以等效热网络法为理论基础,分别求解得到行星减速器的稳态温度场和瞬态温度场分布情况,并同试验结果对比,验证了理论研究的合理性。
1 等效瞬态热网络模型
1.1 电机节点布置及热网络图建立
考虑到起重机用永磁电机结构特点以及等效热网络法网格划分的原则,在电机轴向长度上共划分成44个节点,电机节点分布如图1所示。
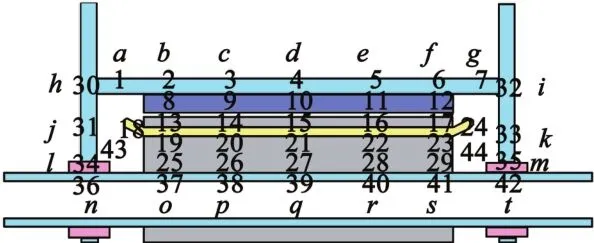
图1 细长型外转子电机节点分布图
图1 中单元1~7为转子外壳温度节点;单元8~12为永磁体温度节点;单元13~17为定子齿部温度节点;单元18~24为定子绕组温度节点,单元18和24为绕组端部;单元25~29为电机定子轭部温度节点;单元30~33为电机端盖温度节点;单元34、35为电机轴承温度节点;单元36~42为电机空心转轴温度节点;单元43,44为电机机腔空气温度节点;单元a~m外部空气;单元n~t空心轴内部空气。图2给出了永磁电机的热网络节点连接图。
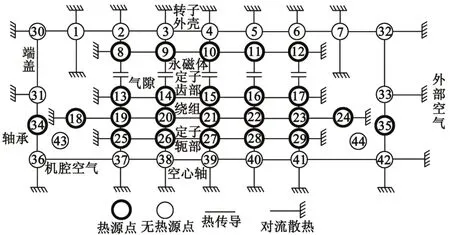
图2 细长型外转子电机等效热网络分布图
1.2 热阻分析和计算
本文将按照细长型外转子永磁电机的结构,在电机定子铁心轴向长度上平均分为5部分,本文只列举了电机的定子和绕组部分热阻计算。
在网格划分时,定子结构划分成以下3部分:定子轭部、定子齿部以及定子绕组,下面对各部分热阻进行分析与计算。
(1)定子轭部
定子轭部轴向共分为5个节点,以节点27为例进行计算分析,定子轭部的热量主要有以下4条传递方式:
①定子轭部节点27到空心轴节点39的热阻:
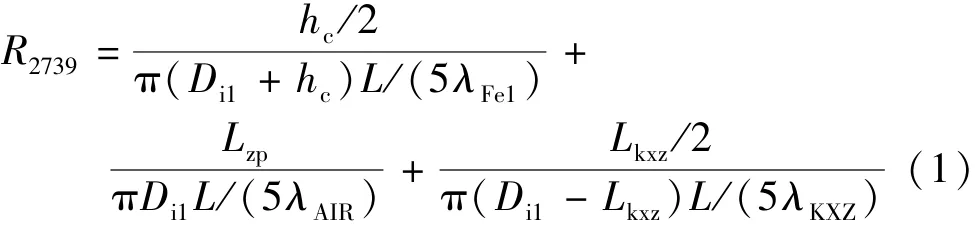
式中:Di1为定子内径;hc为轭部厚度;Lkxz为空心轴的厚度;L为定子铁心长度。
②定子轭部节点27到轭部节点26的热阻:

式中:Ks1为定子槽中绕组等效系数;r1为梨形槽半径;Q1为定子槽数。
④定子轭部节点27到齿部节点15的热阻:
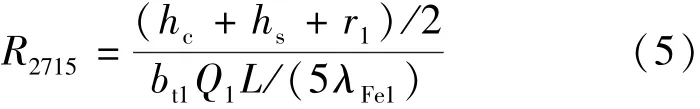
式中:hs为定子槽高;bt1为定子平均齿宽;λFe1为硅钢片径向导热系数。
(2)定子齿部
定子齿部沿轴向共分为5个节点,以节点15为例进行计算分析,定子齿部的热量主要有以下4条传递方式:
①定子齿部节点15到永磁体节点10的热阻[8]:
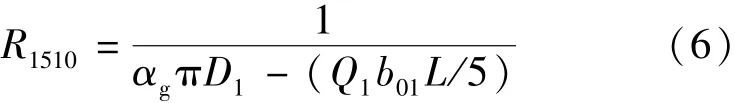
式中:αg为电机气隙等效散热系数;D1为定子外径;b01为定子槽口宽。
②定子齿部节点15到齿部节点14的热阻:
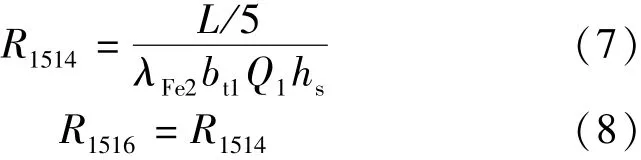
式中:λFe2为硅钢片轴向导热系数。
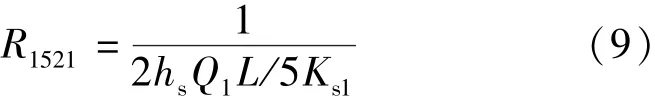
④定子齿部节点15到定子轭部节点27的热阻:

(3)定子绕组
定子绕组轴向共分为7个节点,以节点18(绕组端部)为例进行计算分析定子绕组的热量主要有以下两条传递方式:
①定子绕组端部节点18到内部空气节点43的热阻:
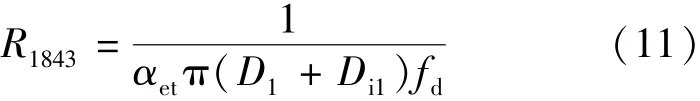
式中:αet为绕组端部等效散热系数;fd为绕组端部长度[9-12]。
②热量在绕组内沿轴向传递热阻:
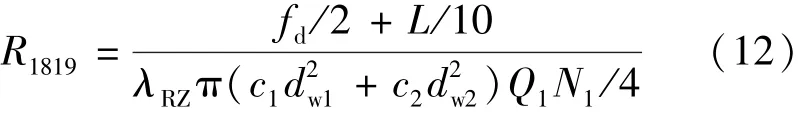
式中:c1,c2分别为第一组、第二组的并绕根数;dw1,dw2分别为第一组、第二组导线裸线半径;N1为每槽导体数。
2 热导方程组及其求解
本文基于MATLAB语言建立方程组并求解,对于任意温度节点i的瞬态热平衡方程[13]:
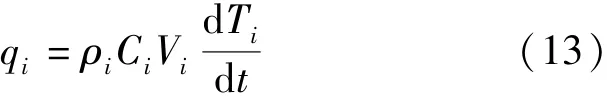
式中:ρi,Ci,Ti和Vi分别表示第i个节点处的净热流量、材料密度、温升值和对应体积;t为时间;表示第i个节点处的温升率。
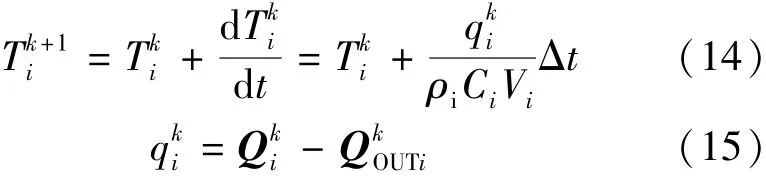
则tk+1时刻温度场Tk+1i(i=1,2,3,…,n),可以通过tk时刻的温度场Tk i递推得到:式中:Qki为第k时刻,功率在该节点上的发热量,是44×1的热源矩阵;QkOUTi为流出该节点的热量,也是44×1的热源矩阵。
构建出定子轭部节点27、定子齿部节点15以及绕组端部节点18的瞬态热网络方程:
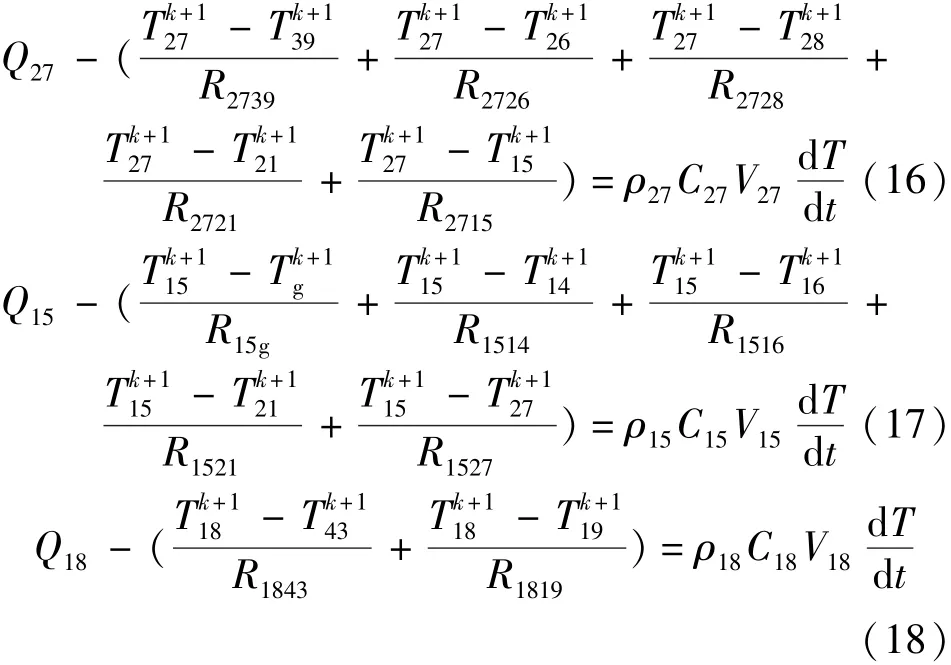
3 瞬态温度场结果分析
表1给出了一台转子外径400 mm的起重机用细长型外转子永磁同步电机部分设计参数。
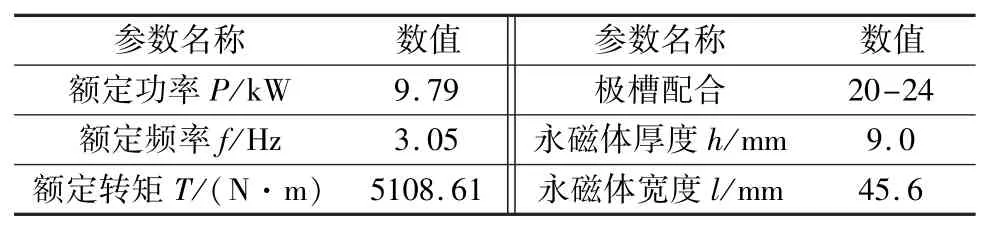
表1 起重机用永磁电机样机设计参数
3.1 时变铜损耗瞬态温度场分析
本文基于MATLAB语言将起重机用永磁电机基本电磁设计程序和瞬态等效热网络程序相结合,对起重机用永磁电机运行过程中铜损耗不断修正,实现电磁场与温度场耦合计算分析。图3给出了基于瞬态热网络法的细长型外转子永磁电机绕组铜损耗的修正计算流程。
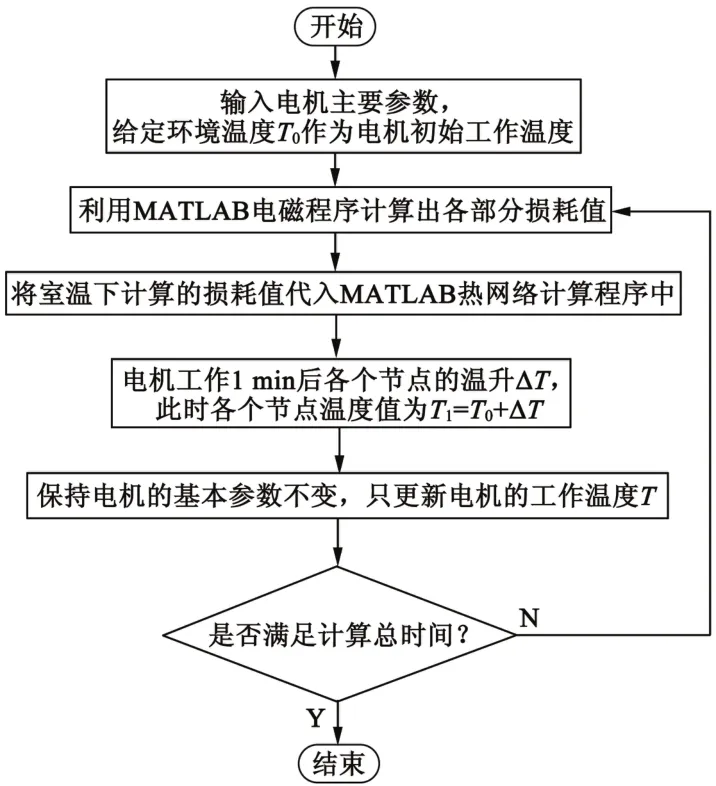
图3 基于瞬态热网络法绕组铜损耗实时计算流程图
如图4所示,对于转子外径400 mm起重机用永磁电机,初始运行和温升稳定后的铜损耗值相差约290W,因而对绕组铜损耗的修正还是很有必要的。图5是基于ANSYS三维温度场有限元仿真分析时,绕组部分生热率的时变加载值。
图6和图7给出了时变铜损耗加载方式下的绕组与整机温度场分布图,温度最大值出现在绕组端部,最大温度值为65.10℃,最大温升为43.1℃。
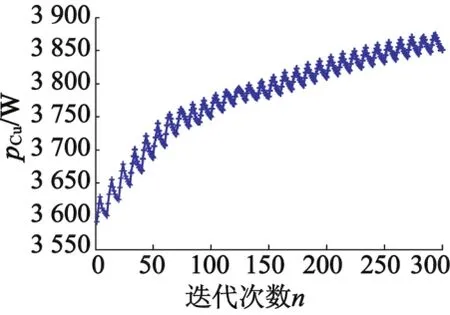
图4 转子外径为400 mm永磁电机绕组铜损耗时变值
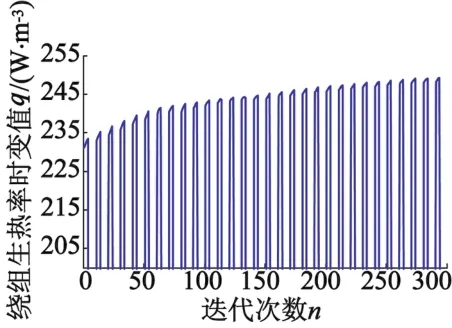
图5 绕组生热率时变加载值
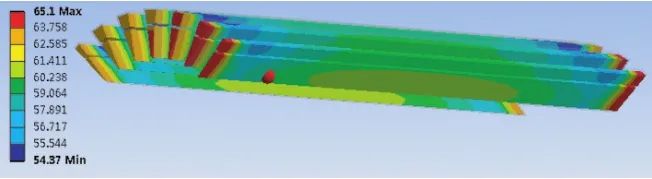
图6 40%通电持续率下的绕组温度场分布图
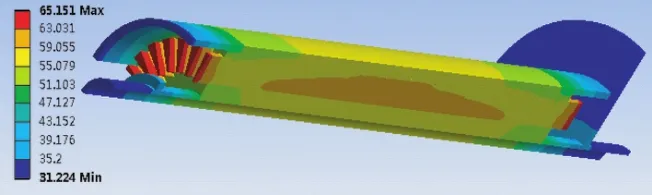
图7 40%通电持续率下的整机温度场分布图
3.2 转子外壳与空心轴散热系数分析
由于本文中电机为外转子永磁电机,热量主要通过机壳表面和空心轴传递到外部,因而需要对两部分的散热系数准确计算分析。
1)转子外壳散热系数
在《大型电机发热与冷却》中电机转子外壳散热系数的经验式如式(19)、式(20)所示。转子外壳表面附近空气漩绕,在利用公式计算时,应按照圆周速度的75%来进行计算。

式中:ω为大气压下空气的运动速度。由式(19)可求取转子外壳散热系数为α1=17.56W/(m2·K)。
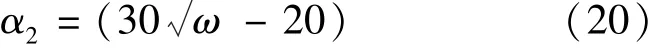
式中:ω为大气压下空气的运动速度[14]。由式(20)可求转子外壳散热系数为α2=30.47W/(m2·K)。
2)空心轴散热系数
电机空心轴起到固定作用,空心轴内壁不通风,属于自然冷却状态。
电机散热系数的经验公式[14]如下:
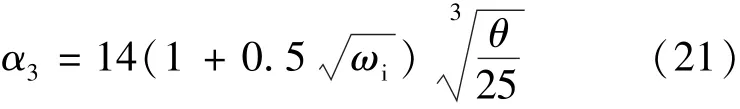
式中:ωi为吹拂机座表面的风速;θ为机座壁外表面的温度。由式(21)可求取空心轴自然冷却散热系数α3=15.2W/(m2·K)。
电机散热系数的经验公式如下[13]:
α4=9.73+14V0.62x(22)
式中:Vx为散热片间的风速。由式(22)可求取空心轴自然冷却散热系数α4=9.73 W/(m2·K)。
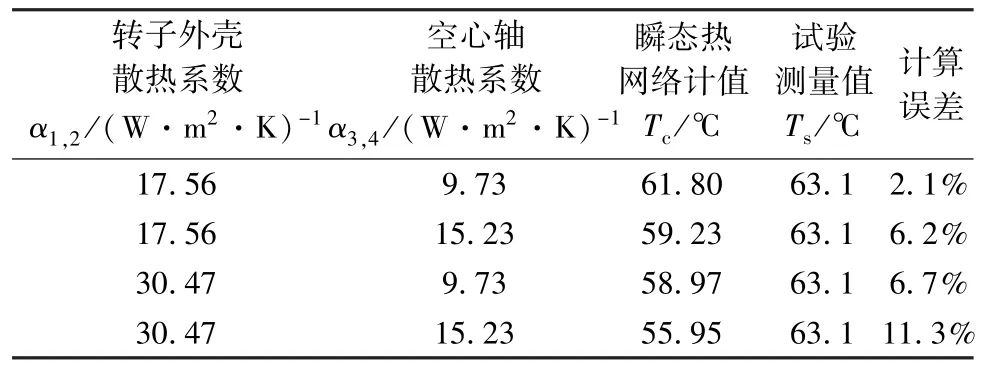
表2 不同散热系数下的绕组端部温度最大值
对比4种不同散热系数方案,由表2可知,最后确定转子外壳散热系数为17.56 W/(m2·K),空心轴的散热系数为9.73 W/(m2·K)。此时,基于等效瞬态热网络法计算得到的绕组端部温度最大值为61.80℃,计算误差最小,误差为 2.1%。
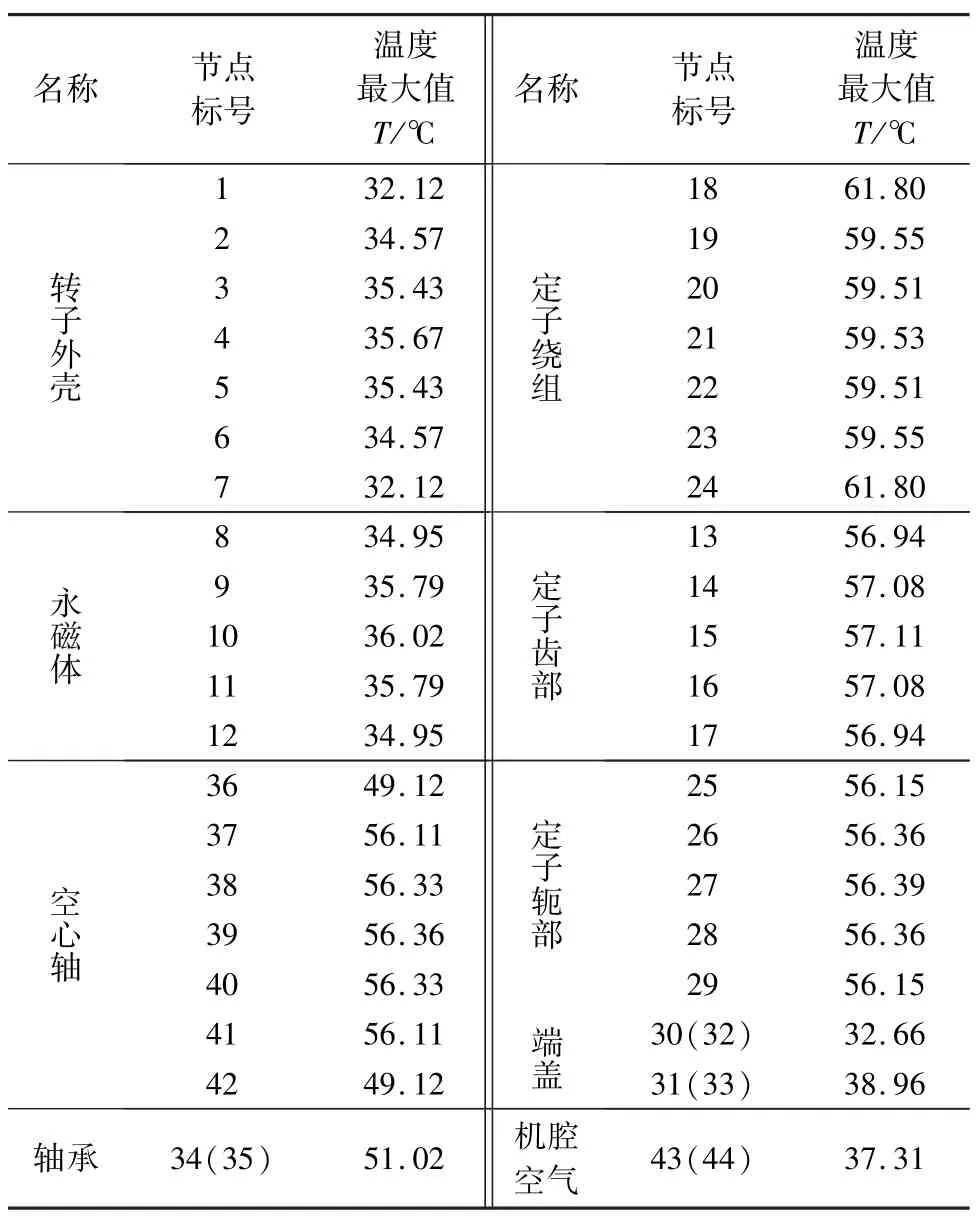
表3 电机温升稳定后各节点最大温度值
4 样机温升试验
本文对一台转子外径400 mm样机进行温升试验。试验过程中采用S3工作制40%通电持续率,每10 min内,运行4 min,停机6 min。本文研究的是细长型外转子永磁电机,受到试验条件和结构限制,通过工业用同步皮带从而达到加载的目的,如图8所示。
如图9所示,绕组端部理论计算值与试验测量值的温度变化趋势基本相符合,但是随着温度值的不断升高,两种计算结果开始出现偏差。温升稳定后,试验测得的最大温度值为63.1℃,而瞬态热网络计算得到温度值最大为61.80℃,相差1.3℃。

图8 转子外径400 mm样机温升试验平台
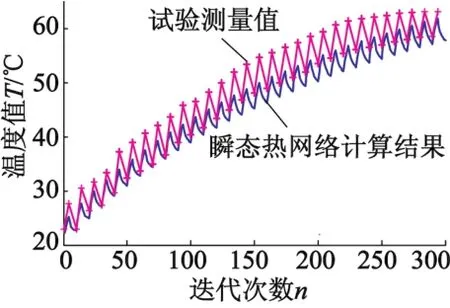
图9 绕组端部温度试验值与热网络计算结果对比图
试验中对起重机用永磁电机绕组端部、空心轴内壁(外端)和转子表面温度最大值,表4给出了瞬态热网络理论计算和试验测得最大温度值对比。
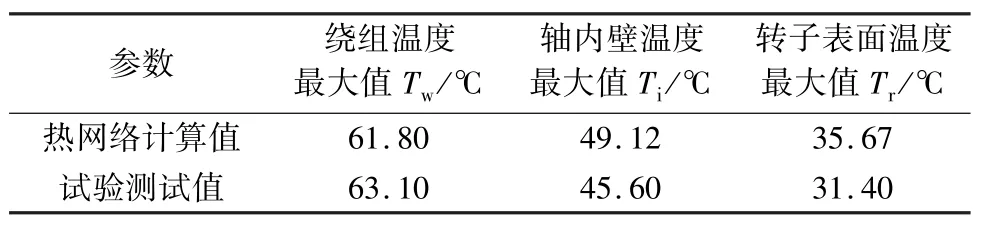
表4 理论计算和实测温度最大值
由表4可知,电机温升稳定时,电机绕组端部的瞬态等效热网络计算结果和试验测试最高温度值分别61.80℃,63.10℃,误差为 2.1℃;试验过程中对空心轴内壁两端进行温度测试,误差为3.52℃;转子表面计算误差为4.27℃。对比两个计算结果分析,瞬态热网络计算结果电机中心温度值低于试验值,可能由于定转子气隙等效散热系数计算值较大,导致绕组产生的热量较易通过气隙,传递到转子外壳;而电机空心轴采取自然冷却方式,散热系数随着温度不断变化,空心轴内壁的散热系数难以给定,导致了两种计算结果存在了一定的误差。
5 结 语
本文基于MATLAB语言建立了起重机用永磁电机热网络模型,详细分析永磁电机各节点的热阻,建立瞬态热方程组并求解,得到以下结论:
1)本文对电机运行过程中的铜耗值进行实时的修正,并提出了绕组铜耗时变加载方式,其计算结果能够较为准确地呈现了起重机用永磁电机运行过程中温升变化过程。
2)为了更加准确的计算电机局部过热点,本文中针对外转子电机的特点,对电机转子外壳与空心轴散热系数进行分析计算,确定其散热系数。本文提出的瞬态热网络模型计算结果较准确,对细长型永磁电机设计及热计算有重要指导意义。
[1]凌文星.电机温升分析研究[J].机电技术,2010(3):66-67.
[2]张建忠,姜永将.基于等效热网络法的定频双转子永磁风力发电机的热分析[J].电工技术学报,2015,30(2):88-97.
[3]魏永田,孟大伟.电机内热交换[M].北京:机械工业出版社,1998.
[4]FAIZ J,GANJIB,CARSTENSE SE,et al.Temperature rise analysis of switched re-luctance motors due to electromagnetic losses[J].IEEE Transacti-ions on Magnetics,2009,45(7):2927-2934.
[5]何磊,王心坚.基于热阻网络法的电机瞬态温度场分析[J].佳木斯大学学报,2014,32(2):187-190.
[6]黄飞.基于热网络法的行星减速器热分析[D].南京:南京航空航天大学,2011.
[7]MELLOR P H,ROBERTS D,TURNER D R.Lumped parameter thermalmodel for electricalmachines of TEFC design[J].1991,138(5):205-218.
[8]ROSTAMIN,FEYZIM R,PYHÖNEN J,et al.Lumped-parameter thermalmodel for axial flux permanentmagnetmachines[J].IEEE Transactions on Magnetics,2013,49(3):1178—1184.
[9]邱洪波,王瑞阳,魏云冰,等.等效热网络法在永磁伺服电动机温度场研究中的应用[J].微特电机,2016,44(3):16-21.
[10]杨世铭,陶文铨.传热学[M].北京:高等教育出版社,1998.
[11]陈世坤.电机设计[M].北京:机械工业出版社,1990.
[12]黄国治,傅丰礼.Y2系列三相异步电动机技术手册[M].北京:机械工业出版社,2004.
[13]杨攀.基于热网络法的直升机主减速器热分析[D].南京:南京航空航天大学,2013.
[14]丁舜年.大型电机的发热与冷却[M].北京:科学出版社,1992:165-169.

