有限元动态模型的修正方法综述

李 杰

（天津航天瑞莱科技有限公司上海分部，上海 201199）

有限元动态模型的修正方法综述

李 杰

（天津航天瑞莱科技有限公司上海分部，上海 201199）

结构在进行有限元仿真分析时，对比计算结果与实际测试数据，往往存在一定的偏离。针对有限元动态模型，基于实际测试获取的少量数据，采用一定的修正算法，从而减小模型修正后的仿真结果与实测响应数据的误差。通过文献调研，对有限元模型修正的一般方法及其发展进行了归纳和总结。

有限元法；模型修正；优化问题

概述

目前，有限元法已经广泛地应用于航天、船舶、桥梁等工程结构的动力学分析。要得到准确的动力学分析结果，首要的问题就是建立精确的结构有限元模型。但由于对结构（包括数学模型以及物理参数）缺少全面深入的了解，同时有限元分析方法作为工程上一种近似的计算方法，通过建立的有限元模型，常常不能得到结构的真实情况。模型修正技术正是在这样的背景下，通过特定的模型修正来较大地减小分析结果的误差，在解决实际工程问题发挥了重要的作用，也得到了很大程度的发展。同时需要注意的是，有限元模型修正是基于实测或试验结果的方法，实测或试验结果的准确性会较大影响模型的修正有效性。当测试结果本身存在过大的误差，用来修正有限元模型也就意义不大了。

1 动力学模型修正方法

模型修正方法是从20世纪60年代发展起来的，Gravitz[1]首次提出通过飞机地面共振实验数据来修正飞机的柔度矩阵。传统的动力学模型修正方法分为矩阵型法和元素型法。

1.1 矩阵型法

矩阵型法常用的修正参数包括刚度矩阵、质量矩阵和子结构校正因子等。Baruch[2]、Berman[3]等人对该修正方法进行了开创性的工作。张德文基于质量阵和刚度阵的相关性，提出了通过正交性条件和特征方程分别来修正质量矩阵和刚度矩阵的方法。1980年，J. C. Chen[4]提出了矩阵摄动法。该方法在修改结构的物理参数时直接采用实验模态分析所得的模态矩阵和特征值矩阵。Berman[5]利用模态正交性条件对上述方法进行了修正，该方法的优点是不需要完整的模态集。矩阵型法的缺点是改变了原矩阵的稀疏特性，且物理意义不明确。

矩阵型法中常用的方法包括全元素修正、非零元素修正、子结构校正因子修正等，这里简要介绍全元素修正法和子结构校正因子修正法的一般思路及方法。

1.1.1 全元素修正法

该修正方法的原理为在质量正则化条件[Φe]T[M][Φe]下，最小化矩阵各元素的相对误差范数。得到修正的质量矩阵和刚度矩阵分别为

其中

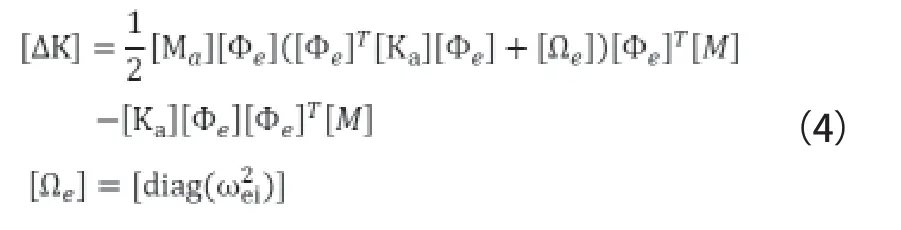
从式（1）可以看出，由于该方法只考虑了正则化条件，而忽略了动力学方程，仅作为一种纯数学处理手段，且修正后的结构矩阵一般情况下不再能正确反映结构的连接情况，同时矩阵的稀疏性和窄带性会受到破坏，给后续的计算和存储带来了很大的代价，很难应用于实际的大型复杂结构。

1.1.2 子结构校正因子修正法

有限元模型的刚度矩阵可以用r个子结构刚度矩阵之和表示

其中为经过扩充和坐标变换的子结构的刚度矩阵（如最简单情况为单元刚度矩阵）。而修正后的刚度矩阵可表示为的加权和形式，即

由式（6）的表达式可以看出，在修正矩阵中，子结构本身的特性不受任何影响，只是改变了其对整个结构矩阵的贡献大小。把式（6）带入模型的动力学方程

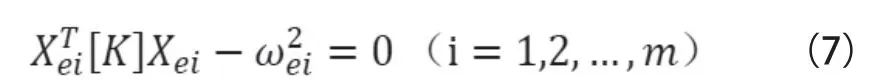
得到

式（8）中含m的方程，r个未知数。当r ≤ m时，求解方程组可得到精确解或最小二乘解。通过求解出的向量（b1, b2, … , bn）T，代入式（6）即可得到修正后的刚度矩阵。对于质量矩阵的修正，同样可以按照这种方法进行。

1.2 元素型法

从80年代末起，元素型法逐渐成了研究的重点。该方法的修正对象为矩阵元素或结构设计参数（包括几何尺寸、材料属性、边界条件和连接刚度等）。

这种修正方法通过对几何尺寸、材料属性、边界条件和连接刚度等一些在有限元建模过程中不容易确定的参数进行调整，从而使结构的模态频率和模态振型发生变化。Q. Zhang和G. Lanllent在研究中，通过对子结构修正因子的灵敏度分析，获得了建立有限元模型的误差并修正未知的结构参数。J. C. Chen在文献[5]中建立了有限元模型的模态频率函数，修正变量为结构的设计参数Pj（Pj表示第j个参数），通过泰勒级数将在初值P0j处展开

应使设计参数Pj修正后模型的模态频率ωi与试验频率ωri接近，应使两者的偏差

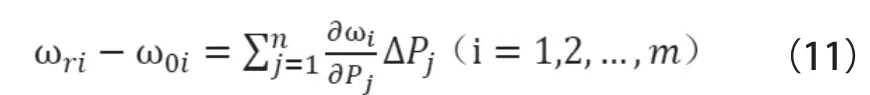
最小，即同样对于模态振型，可表示为

前述方法是基于模态参数的，另一种元素型法是基于频响函数的。这方面的工作可追溯到1977年Natke[7]的研究，即采用加权最小二乘法处理无阻尼问题。后续，Larsson[8]等在利用动刚度矩阵的泰勒级数展开得到新的残差形式后，通过动态缩聚方法，解决了仿真模型与试验模型之间自由度不同的问题。在国内，黄东胜[9]、朱安文[10]等人分别对基于频响函数的模型修正方法进行了相关的研究。

2 动力学模型修正技术的发展

在文献[11]中，吴小菊对当前动力学有限元模型修正中的5项关键技术进行了总结如下：①修正参数的选取；②计算模型与试验模型的维数匹配；③灵敏度分析；④（加权）最小二乘求解正反问题时条件数差的解决方法；⑤修正方法的正确性判断。

有限元动态模型修正技术近年来有了较大的发展。王乐等[12]基于模态频率来修正模型的刚度矩阵。张以帅[13]提出了一种不依赖于灵敏度分析的参数性修正方法，拓展了基于频响函数的矩阵型模型修正方法。周瑞等[14]提出一种新的模型迭代技术—IOR技术应用于基于可测点数据的模型修正。

3 结束语

目前，模型修正技术已广泛应用于航天、航空、汽车、船舶、土木和机械等领域。如加拿大波音公司某飞机模型的修正，美国通用公司轿车白车身的模型修正，斜拉桥有限元模型修正等。对于修正技术的未来发展，当前的一些问题还需要解决：①适用范围窄；②由测量结果的不完整引起的结果不唯一性；③建模中的误差定位，包括模型简化误差、测量误差和模态截断误差；④修正模型主要针对低阶模态；⑤软件实现效率。这些都需要研究者更进一步地探讨和研究。

[1] Gravitz. An Analytical Procedure for orthognalization of Measured [J]. MJAS, 1958, 25(11): 721-722.

[2] Baruch M. and Bar Itzhack I Y. Optimal weighted orthognalization of measured models [J]. AIAA Journal, 1978, 16(3):83-86.

[3] Berman, Flannelly. Theory of incomplete models of dynamic structures [J]. AIAA Journal, 1971, 9(8).

[4] J C Chen, Garba J A. Analytical Model Improvement Using Modal Test Results [J]. AIAA Journal, 1980, 18(6).

[5] Berman A and Nagy E J. Improvement of a Large Analytical model Using Test Data[J]. AIAA Journal, 1983, 21(8): 26-30.

[6] SLJ Hu, H Li, S Wang. Cross-model cross-mode method for model updating [J]. Mechanical Systems and Signal Processing, 2007, 21(4):1960-1703

[7] Natke, H.G., Die Korrektur. Rechenmodells Eines Elastomechanischen Systems Mittels Gemessener Erzwungener Schwinggungen [J]. Ingenieur-Archiv, 1977, 4(6): 169-184.

[8] Larsson, P.O. Model Updating Based on Forced Vibrations[C]. Proceedings of the 4th Conference on Recent Advances in Structural Dynamics. 1991:95-98.

[9]黄东胜, 黄方林, 顾松年.一种改进的动力缩聚及模型修正的方法[J]. 长沙铁道学院学报, 1996, 14(4): 72-77.

[10]朱安文, 曲广吉, 高耀南. 航天器结构模型修正技术的工程应用研究[C]. 2002年全国振动（诊断、模态、噪声与结构动力学）工程及应用学术会议论文集, 北京: 2002.10.16.

[11]吴小菊. 结构有限元模型修正综述[J]. 特种结构, 2009, 26(1): 39-45.

[12]王乐, 杨智春, 李文斌, 谭光辉, 刘江华. 基于固有频率向量的模型修正方法[J]. 西北工业大学学报, 2008,26(1): 93-98.

[13]张以帅. 基于频响函数的有限元模型修正方法及试验研究[D]. 上海:上海交通大学, 2009.

[14]周瑞, 陈力奋. 基于可测点信息的模型参数修正方法[J]. 振动与冲击, 2007, 26(6): 70-74.

李杰，硕士研究生，中级工程师。主要研究结构设计及动力学仿真、动力学试验 。

A Review of Updating Method of FE Dynamic Model

LI Jie
(Shanghai Branch of Tianjin Aerospace Ruilai Technology Co. Ltd., Shanghai 201199)

TDiscrepancies exist between results from a structural FEA model and experimental data from laboratory. The updating method of FE dynamic model is developed to decrease errors by using the measured data of structure. This paper presents the general theory and recent development by review of previous work of modal updating method.

finite element method; model modification; optimization prcldem

O326

A

1004-7204（2017）02-0034-03