生活中的数学

文/许彤曦

生活中的数学

文/许彤曦

数学是自然科学的基础，在我们的日常生活中，有许多问题如果用数学的思想方法去解决，就会显得简单明了。其实数学是非常有趣的，但它的趣味性往往被其复杂的公式和定理所掩盖，让人们退避三舍。如果真正领悟了数学的思想方法，许多问题就变得有趣而且生动了。下面我用中学数学知识和生活当中常见的几个问题做简单的阐述。

1 集合在生活中的应用

集合是数学中一个重要概念。数学知识中描述的集合往往指的是数集，在中学我们学习了许多数集，如实数集，有理数集，无理数集，自然数集等等，同时也学习了集合的各种运算，其实集合这个概念是来源于生活实际问题，在日常生活中，集合描述的是具有相同性质的事物构成的整体。为了研究这个群体的某种性质，我们把这个群体中的每个个体用一个数代替，从而这个群体就与一个数集形成了一一对应关系。例如一个班级中有50个学生，那么这个群体就可以和从1到50的自然数形成一一对应关系，每个学生对应着一个学号，这样即使老师不认识学生，也可以随意的叫一个学生回答问题。还有在图书馆中，每本图书分门别类都有一个序号与之相对应，这样就能方便读者借阅。

集合在生活中还有别的用途。在数学运算中，任意两个数都可以相加的，因此在日常生活中，很多人误认为任何两个事物都可以相加的，但事实并不是如此，其实加法运算必须建立在一定的条件下，在数学中，两个数是抽象的，他们同属于实数集，从而可以相加。在生活中，只有属于同一集合中的两个事物才能相加。在数学上1+1=2是永恒的真理，但生活中一只鸡和一只狗就不能相加，因为鸡和狗不属于集合。同时，集合又有它的内涵与外延，在生活中，如果把有着不同性质的事物进行延拓，使其归属于同一个集合，那么这两个事物就能够相加了，比如说一只鸡加一只狗等于两个动物，这谁能说你是错误的呢？因为鸡和狗属于动物的范畴。

2 函数在生活中的应用

函数是数学中的一个最基本概念，在中学我们学习了许多函数，例如一次函数，二次函数，指数函数，对数函数以及三角函数，这函数在数学中的意义是两个变量之间的一种关系，其实函数这个概念也是来源于实际问题，在日常生活中，任何事物之间都存在着某种联系，为了更好的研究这种关系，我们可以把这种关系量化，从而形成了函数的概念，因此在实际生活中函数的实质是事物之间关系的量化过程。正是由于有了这种量化过程，从而减少了生活当中许多模棱两可的问题，使我们有据可循。

例如，在日常生活中的运输问题，每个人在搭车的时候可以携带一定重量的物体，但如果携带的物品没有限制，就会产生许多纠纷，为了防止这种纠纷的产生，交通部门制定了明确的制度，我们可以用一个简单的函数来描述乘客携带的物品重量与所缴纳的乘运费之间的关系：

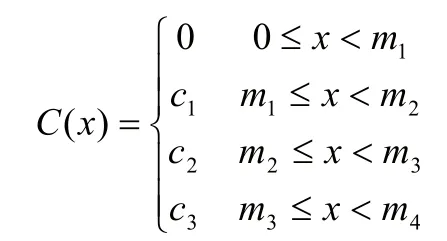
其中x表示乘客携带物体的重量，ci，i=1,2,3表示乘客必须缴纳的费用，有了这个依据，乘客就不会和交通公司发生产生纠纷了。

另外，我们在数学中学习函数，研究函数的各种性质，其实也是为了更好的解决实际问题。例如我们研究二次函数y=ax2+bx+c的最大最小值，根据研究，我们知道当a>0时，该函数有最小值，且当时，其最小值为；当a<0时，该函数有最大值，且当时，其最大值为。那么这在生活中有什么用处呢？其实生活中有很多问题都要用到这个结果。比如说，我们用周长为L的铁丝围成一个矩形，问边长为多少时，该矩形面积最大？我们可以设其边长分别为x，，因此该矩形的面积这就是一个二次函数，其中a=-1，c=0，根据我们在数学中的研究，可以得到当时，其面积最大，且最大值为，即该矩形为正方形时，面积最大。这个研究在我们日常生活中非常有用，比如为什么普通家庭的餐桌都是用正方形，而非别的形状的矩形。这是因为在周长相等时，正方形的面积最大，这样的餐桌可以容纳更多的饭菜。

当然，日常生活中还有许多问题需求数学的知识，才能得以解决。数学源于生活，但又高于生活，数学中的所有思想方法和生活中处理问题的思想方法都是想通的。我们学习数学是为了更好地解决生活中的具体问题，也只有真正领悟了数学的精髓，才能在解决实际问题的时候游刃有余。

（作者单位：湖南省益阳市第一中学）