变频器输出有功功率测量方法研究
李海国, 常 越, 王达开, 张晓斌, 王娇娇
(上海交通大学 电子信息与电气工程学院,上海 200240)
变频器输出有功功率测量方法研究
李海国, 常 越, 王达开, 张晓斌, 王娇娇
(上海交通大学 电子信息与电气工程学院,上海 200240)
讨论了变频器测量自身输出功率的两种方法:通过输出相电流的FFT变换获取基波幅值和相位,利用PWM调制波为输出相电压基波的特点获取输出电压基波幅值和相位,从而计算有功功率;近似相电流为基波电流,对电流进行采样并与相应时刻的PWM调制波数值相乘得到瞬时功率,在输出电压一个周期内对瞬时功率累加后求平均得到有功功率。FFT方法对电流谐波的抗干扰能力强,对相电流基波幅值和相位的获取准确,但占用CPU资源较多;周期内瞬时功率求平均方法计算简单,CPU资源消耗低,但对电流谐波敏感。经过对实际运行变频器输出功率的测量,表明叙述的变频器自身测量输出功率的方法是可行的。
变频器;有功功率测量; 脉宽调制
0 引 言
变频器是大量使用的电机调速设备,很多应用场合需要测量变频器的输出功率,也有许多使用变频器的场合额外安装了功率测量设备。本文旨在讨论利用变频器自身的控制系统测量变频器输出功率的方法。

图1 变频器逆变电路
变频器常用拓扑为电压源型三相逆变电路,如图1所示。该拓扑还在交流稳压源、有源逆变器等设备中应用[1]。在实际控制中会对直流母线电压UD进行采样,以此来计算调制比,从而实现输出正弦电压调幅。为了测量输出功率,需要在变频器上安装电流传感器测量输出电流。为了使变频器自身完成输出功率测量,本文采样单相电流后计算单相有功功率再乘3得到三相有功功率输出。
正弦脉宽调制(Sinewave Pulse Width Modulation,SPWM)是采用标准的正弦波作为PWM调制波,输出电压基波也具有与调制波同样的性质。在直流母线电压不变的情况下,输出相电压基波幅值随调制比线性变化,相位与调制波相位一致[2-3]。所以,在SPWM程序中,总是知道输出相电压的基波幅值U和相位φ。
变频器输出相电压(后如无特殊说明,相电压均指相电压基波)、相电流(后如无特殊说明,相电流均指相电流基波)为有相位差的正弦波。令电压初相角为零,设电流初相以-φ表示(电流滞后电压时φ取正),则相电压、相电流波形如图2所示。

图2 变频器输出相电压、相电流波形

(1)
式中:u——相电压瞬时值;U——相电压幅值;i——相电流瞬时值;I——相电流幅值;w——相电压、相电流角速度,w=2πf;f——变频器输出电压频率。
本文基于三相逆变的SPWM,利用直流母线电压UD、输出相电流i、相电压幅值U、相位wt,详细论述了如何计算三相变频器输出有功功率(基波有功功率)。该方法同样可以在单相SPWM、三相空间矢量脉宽调制(Space Vector Pulse Width Modulation,SVPWM)等应用中推广。
1 有功功率
交流电路的有功功率是一个周期内电路传输的瞬时功率平均值。计算方法如式(2)所示。
(2)
式中:T——交流电周期;u(t)——电压瞬时值;i(t)——电流瞬时值。
如果电压、电流都是正弦波,如式(1)所示,则有功功率计算为
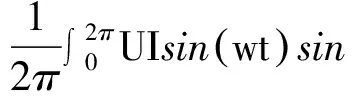
(3)
对于含有谐波的非正弦电路,电压、电流可以用傅里叶级数表示成式(4)的形式。
(4)
由于sin(wt+φ1)、sin(2wt+φ2)、sin(3wt+φ3)…都是互相正交的,即不同频率的正弦波乘积在一个周期里的积分为零[4],如式(5)所示,故有功功率计算如式(6)所示。

(5)
(6)
式中:Un、In——n=0为直流分量,在变频器中U0=0,I0=0;
n=1——电压电流基波幅值;
n≥2——电压电流n次谐波分量幅值;
φn——n次分量的电压、电流相位差,对应式(4)有φn=δn-θn;
Pn——n=1时为基波有功功率;n=2,3,4…时为n次谐波的有功功率。
所以,在含有谐波的交流电路中,有功功率等于基波有功功率加上各次谐波有功功率。因为变频器的负载往往是大电感,或者在变频器输出端口加装有滤波器,电流波形正弦性很好。相对于基波有功功率,采用SPWM和SVPWM算法控制的变频器输出的谐波有功功率很小。除此之外,在很多情况下,谐波有功功率并不是期待的功率输出。对于电机负载,谐波有功功率主要是铜损和机械的振动、噪声[5],并没有产生实际的输出转矩。所以,对于变频器输出有功功率只考虑其基波有功功率是可以理解的。本文所介绍的有功功率计算方法是针对电压基波和电流基波的基波有功功率(后无特殊说明,有功功率均指基波有功功率),忽略了谐波的影响。
2 方法一:FFT变换
2. 1 求有功功率
根据前文所述,计算有功功率,需要知道相电压幅值U、相电流幅值I和电压电流相位差φ。对于SPWM,是将输出电压波形作为调制波,与三角波(载波)进行比较来确定PWM占空比。所以,U就是SPWM调制波的幅值,在程序调制算法中是已知量,关键要求取I和δ:可对输出相电流采样值进行FFT得到。

(7)

(8)
可知,k的取值范围可以为1,2,3…N/2。但为了精度更高,往往会选择fs=Nf0,并且N尽可能取大一点。
PWM过程中知道相电压u的实时相位wt,如果在相电压相位φu=0时,开始一个周期的电流采样,对电流FFT变换后得到电流基波频率的相位φi,那么电流电压相位差φ=φi-φu=φi。
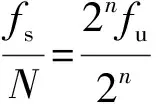
(9)
(10)

图3 FFT采样点图示
2. 2 THD和功率因数
通过FFT得到了相电流基波幅值,如果知道相电流有效值,就可以计算相电流的谐波畸变率THD。在数字系统中将交流电流有效值计算公式(11)离散化得到数字计算公式(12)[6]。
(11)
(12)
式中:N——一个周期内的采样点个数,N等于采样频率除以变频器输出频率;
ik——采样电流值。
利用FFT的采样点数据,按照式(12)就可以直接计算出相电流有效值,则电流的谐波畸变率可按式(13)计算。
(13)

如果认为变频器电压波形为正弦波(谐波可忽略),则功率因数:
(14)
式中:U——变频器输出相电压幅值;φ1——相电流基波与相电压的相位差。
3 方法二:周期内瞬时功率求平均
FFT方法需要消耗一定的CPU资源,运算量也比较大。当相电流正弦性很好时,可以近似实际测量的电流波形为电流基波。所以,可以直接将相电压、相电流相乘,并在一个周期内进行积分从而得到有功功率,即按照式(15)计算。
(15)
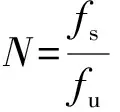
通过定时器来对变频器输出相电流进行周期性采样,采样频率为fs,在每一个采样时刻还需获取PWM调制波的瞬时值uk,将每个采样点的电流值与对应的电压值uk相乘并累加起来,一个电压周期结束后再除以采样点个数,即算得有功功率。
4 误差分析
4. 1 开关管压降
两种测量有功功率的方法都使用了PWM调制波幅值,但变频器实际输出相电压为方波(出口未加滤波器情况),PWM调制波实际上是输出相电压的基波。方波信号中以调制波为主,还有直流母线的整流脉络、PWM斩波频率分量等。
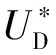
(16)
4. 2 死区时间
为了防止同桥臂上下管子的直通,需要在上下桥PWM上加入死区。死区的插入影响了输出方波的宽度,从而会影响输出电压基波幅值、正弦性和相位。增加死区会导致实际输出电压基波幅值下降、相位超前角增加。死区的加入还会引入低次谐波,谐波幅值与死区时间占比成比例[2]。在PWM中可以通过死区补偿来尽量减小死区的影响。死区补偿的前提是知道电流的方向,所以需要在输出三相上都装上电流传感器[7-8]。
4. 3 电压、电流谐波
FFT方法是基于相电压、相电流基波和两者相位差进行计算的,得到的是基波有功功率,电流、电压谐波的影响较小。周期内离散累加方法是将相电流近似为基波电流,所以电流谐波会产生影响。只有电流谐波很小时,计算精度才高;电流谐波越大,则近似度就越小,计算误差就会越大。
4. 4 采样精度
PWM斩波过程可能会对数字采样系统产生干扰,从而使直流母线电压和输出电流的采样精度受到影响,可以在PWM高、低电平的中点触发ADC采样,这样就避开了PWM斩波时刻电压、电流的尖峰干扰,从而保证采样精度。但FFT方法的电流采样不能使用此触发方式,因为电流采样频率需要是输出电压频率的2n倍,要求时间是等间隔的,采样时间点不能与PWM的高、低电平的中点一直保持一致。
4. 5 CPU运算速度
两种方法都需要乘除运算,方法一甚至还有开根运算等,CPU资源有限,并且运算速度必须高于ADC采样周期。对于很多处理芯片,可能运算速度达不到要求,可以通过程序优化、调用算法库等方法来提高。本文在实际应用中,使用了飞思卡尔的嵌入式软件电机控制和电源转换库,极大地加快了运算处理速度,实现了有功功率的测量。
5 结 语
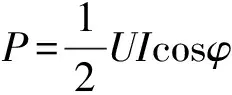
[1] 陈坚,康勇.电力电子学——电力电子变换和控制技术[M].北京: 高等教育出版社,2012.
[2] 徐德鸿,马皓,汪槱生.电力电子技术[M].北京: 科学出版社,2012.
[3] 林渭勋.现代电力电子技术[M].北京: 机械工业出版社,2013.
[4] 王兆安,杨君,刘进军,等.谐波抑制和无功功率补偿[M].北京: 机械工业出版社,2015.
[5] ORFANIDIS S J. Signal Processing[M].北京: 清华大学出版社,2010.
[6] 罗利文,盛戈皞,张君,等.电气与电子测量技术[M].北京: 电子工业出版社,2011.
[7] 张兴,张崇巍.PWM整流器及其控制[M].北京: 机械工业出版社,2013.
[8] QIU T F, WEN X H. Adaptive-linear-neuron-based dead-time effects compensation scheme for PMSM drives[J]. IEEE Transactions on Power Electronics, 2016, 31(3): 2530-2538.
Research of Measurement Methods for Output Active Power of Inverter
LIHaiguo,CHANGYue,WANGDakai,ZHANGXiaobin,WANGJiaojiao
(School of Electronic Information and Electrical Engineering, Shanghai Jiaotong University, Shanghai 200240, China)
Two methods to measure the output power of inverter was discussed: calculating the output active power by getting the fundamental amplitude and phase of the output phase current through the FFT transform and obtaining the fundamental amplitude and phase of the output phase voltage according to the features of PWM modulation wave; regarding the phase current as fundamental current, and calculating the active power by average the instantaneous power within a period, which came from the sample current multiply PWM modulation value. The FFT method had a strong anti-interference ability to the harmonic current, and could obtain fundamental amplitude and phase accurately, yet it required more CPU resources. The latter method was simple in calculation and required less CPU resources, but it was sensitive to current harmonics. The experiment of the actual system showed that the methods to measure output power of inverter was workable.
inverter; active power measurement; pulse width modulation (PWM)
李海国(1990—),男,硕士研究生,研究方向为电力电子与电力传动。 常 越(1959—),男,副教授,研究方向为电力电子与电力传动。 王达开(1993—),男,硕士研究生,研究方向为电力电子与电力传动。 张晓斌(1992—),男,硕士研究生,研究方向为电力电子与电力传动。 王娇娇(1994—),女,硕士研究生,研究方向为电力电子与电力传动。
TN 773
A
1673-6540(2017)04- 0107- 05
2016 -09 -30

