一种新型搜索电机转子频率的方法*
胡文豪, 吴振兴, 孙 乐, 蔡信健
(1. 海军工程大学 舰船综合电力技术国防科技重点实验室,湖北 武汉 430033; 2. 西安交通大学 电气工程学院,陕西 西安 710049; 3. 华中科技大学 电气工程学院,湖北 武汉 430074)
一种新型搜索电机转子频率的方法*
胡文豪1, 吴振兴1, 孙 乐2, 蔡信健3
(1. 海军工程大学 舰船综合电力技术国防科技重点实验室,湖北 武汉 430033; 2. 西安交通大学 电气工程学院,陕西 西安 710049; 3. 华中科技大学 电气工程学院,湖北 武汉 430074)
针对高压变频调速系统,提出了一种新型的“飞车起动”控制算法。该算法无需配置电压互感器及转速传感器,仅由定子电流幅值的大小即可快速搜索出旋转电机的转速。为了实现该功能,推导了维持定子电流恒定时,定子电压与输出频率、电机转速之间的稳态数学表达式,证明了定子电流与电机估计转速之间具有单调递增的函数关系,并获得了该函数关系成立的限制条件。在此基础上,在搜频过程中,算法根据设定的规律动态改变变频器的输出频率,提高了电机转子频率搜索的快速性和准确性。仿真结果验证了理论分析的正确性和所提方法的有效性。
转子频率搜索;高压变频器;飞车起动;异步电机
0 引 言
大功率高压变频器广泛应用于各行业的风机、泵类等设备,在降耗节能、改善工艺等方面起着重要的作用[1-2]。随着系统应用领域的扩大,很多应用场合都要求高压变频器具备“飞车起动”功能[3-4]。
高压变频器的“飞车起动”是将高压变频器直接接入正处于自由旋转状态的三相异步电机,然后拖动该电机运行至额定转速的过程。实现“飞车起动”的关键是变频器的输出频率必须与转子转速频率相同,以减小转差频率,避免起动过程中的定子过流和变频器直流侧过压等问题。对于没有配置转速传感器的电机,其转子频率难以准确获知,因此首先必须对其进行搜索,通常有如下几种搜索电机转子频率的方法:
(1) 文献[5]通过检测电机的反电动势,利用反电动势频率间接估算电机转子频率。但电机反电动势会在电机惰转数秒内衰减至接近于零,此时该方法就达不到期望的效果。
(2) 文献[6-7]通过在电机上施加一个初值电压,利用检测到的定子电压、电流等物理量来估计转速。实际实施时,为了防止过流只能给电机加一个较小的初值电压,导致搜索到的转子频率精度较低。
(3) 文献[8]提出一种“定子输入恒定电流的U/f曲线电压比较法”,即通过电流控制器调整变频器输出电压维持定子电流恒定,然后逐渐降低变频器输出频率,实时比较恒定电流的U/f曲线与恒定磁通的U/f曲线上的电压值,当二者相等时,此时变频器的输出频率即为转子频率。此方法的难度在于维持定子电流恒定的电流控制器以及变频器输出频率下降控制策略的设计。此方法通常搜频时间较长,限制了算法的控制效果。
本文提出一种根据定子电流幅值来搜索电机转子频率的控制策略。算法根据电机的估计转速动态改变变频器的输出频率,加快了转速搜索的速度,提高了转速搜索的精度。最后通过仿真验证了理论分析的正确性和所提方法的有效性。
1 转子频率搜索原理
本文根据定子电流幅值的大小来调整估计转速,使其接近电机转速。当定子电流为指令电流值时,估计转速近似等于电机转速,即表明搜索频率成功。为此,首先需要推导定子电流为恒定值时,定子电压与输出频率和电机转速之间的稳态数学表达式;其次分析若将以估计转速取代电机转速代入此数学表达式得到的定子电压输入电机时,定子电流与估计转速、输出频率和电机转速之间的函数关系。这为本文控制系统构建及控制参数设计提供理论依据(本文所有的定量分析、图表数据及仿真说明均是基于表1的电机模型参数而开展的)。

表1 电机模型参数设置
1. 1 定子电流为恒定值时输出电压与输出频率和电机转速的稳态数学表达式
此数学表达式的推导基于笼型异步电机矢量控制系统按转子磁链定向的动态模型[9],并对微分项进行近似忽略,最终得到的是稳态数学表达式。
1. 1. 1 数学表达式推导过程
笼型异步电机基于动态模型按转子磁链定向时,ω-ψr-is状态方程式如下:
(1)
式中:ism、ist,usm、ust,ψrm、ψrt——MT两相旋转坐标系下定子电流幅值、定子相电压幅值、转子磁链m、t轴分量;
ω1——输出角频率;
ωr——转子电角频率;
Ls、Lr、Lm、Rs、Rr——定子自感、转子自感、互感、定子电阻及转子电阻;
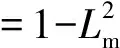
Tr——转子电磁时间常数,Tr=Lr/Rr。
忽略式(1)中的微分项,即取dψrm/dt=0,dism/dt=0,dist/dt=0,可得到稳态下定子相电压幅值Us的数学表达式如式(2)所示。
(2)
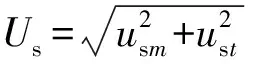
当式(2)中定子电流幅值Is取为某一定值时,则最终可得到定子电流为恒定值Is0时定子相电压幅值Us的数学表达式如下:
(3)
式中:Is0——取为0.7倍额定电流值,ω1≥ωr。
根据式(3)可以绘出定子电流为Is0时,不同电机转速ωr下,定子相电压幅值Us与输出频率fs(fs=ω1/2π)的关系曲线如图1所示。
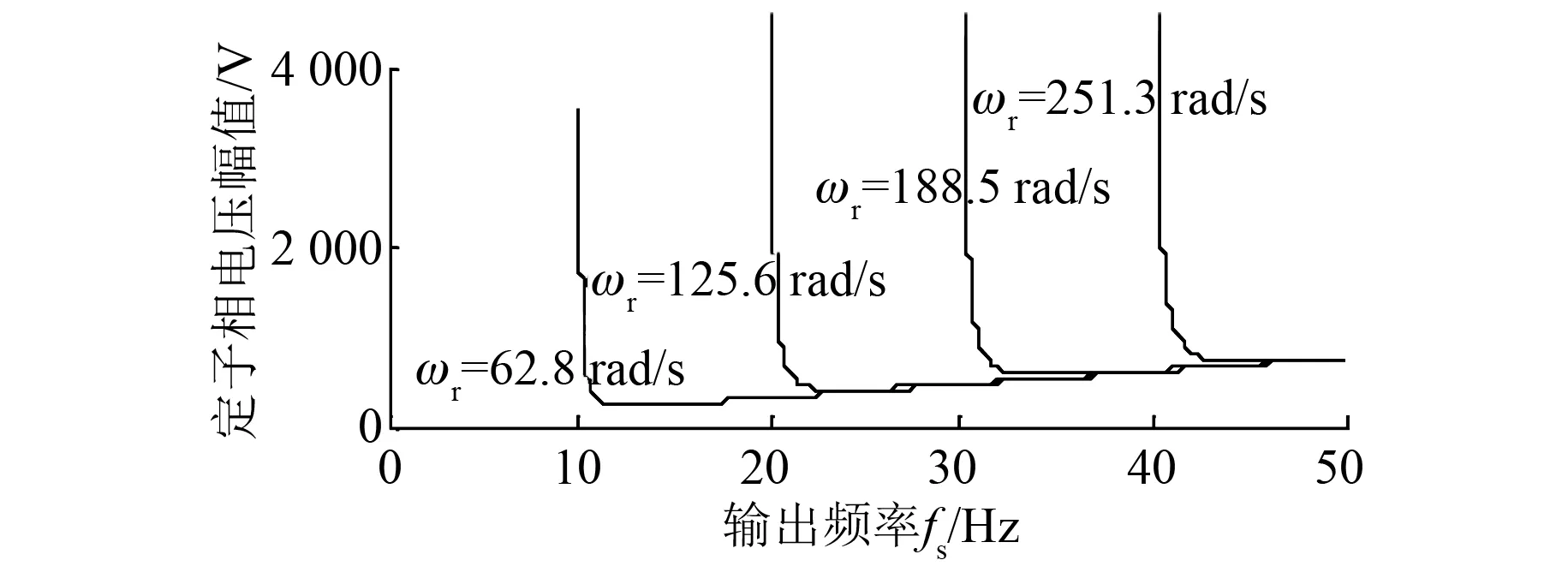
图1 Is=Is0时,不同ωr下Us与fs的关系曲线
1. 1. 2 恒定定子电流稳态数学表达式在动态模型下的适用条件
式(3)是稳态下的数学表达式,而本文的控制系统需要具有高动态性能。在动态过程的影响下,式(3)可能不再适用。图2为电机转速取ωr=2π×30 rad/s,输出频率fs以不同的速率从50 Hz降低到30 Hz后保持不变,进而模拟不同程度的动态过程,即依据式(3)输出电压时定子电流幅值Is与时间t的仿真波形。

图2 ωr=2π×30 rad/s,不同的fs下降率对应的电流波形
由图2可以看出,输出频率fs下降速率越快,动态过程对稳态数学表达式(3)影响越大,定子电流无法一直保持为恒定值Is0。
由图2同时也可以看出,只有在输出频率fs接近电机转速ωr时动态过程才会对稳态数学表达式有较大影响。当输出频率大于某一频率的条件下,采用稳态数学表达式,定子电流同样可以维持恒定电流值。
结合图1及式(1)进行分析,造成上述情况的原因是当输出频率fs接近电机转速ωr时,定子电压幅值Us变化率很大,即dUs/dt很大,导致微分项dism/dt与dist/dt无法近似忽略。综上所述,只有当Us变化率较小时,稳态数学表达式(3)才适用于动态模型。
经仿真验证,当输出频率fs大于图1中曲线的极小值点(拐点)对应的输出频率fs0时,Us变化率较小,可以应用稳态数学表达式(3)保持定子电流为恒定值Is0。不同电机转速ωr对应的输出频率fs0值如表2所示。
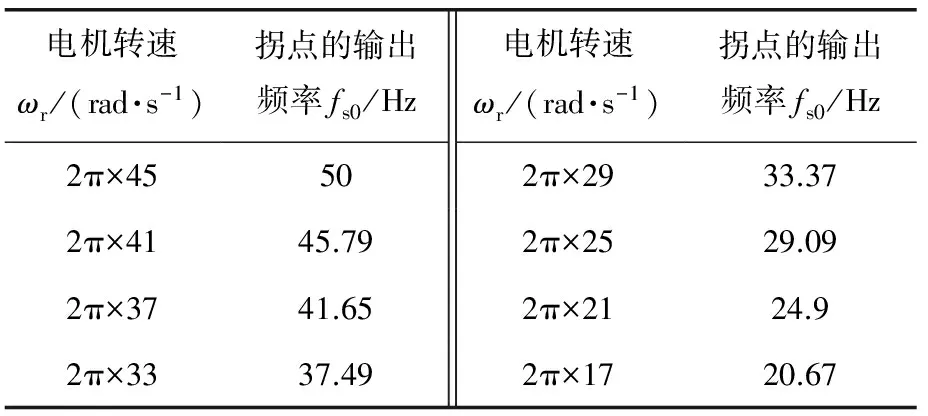
表2 不同电机转速ωr对应的输出频率fs0值
由表2数据可见,表达式fs0=ωr/(2π)+4可基本表征fs0与电机转速ωr之间的关系。故当输出频率ω1与电机转速ωr满足如下条件时,认为恒定电流稳态数学表达式(3)适用于动态模型。
(4)
1.2 定子电流与估计转速、输出频率和电机转速之间的函数关系
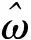
(5)
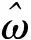
(6)
其中:
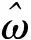
(7)
(8)
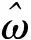
2 控制策略及控制器参数设计
2. 1 控制系统结构
本文的控制系统结构框图如图3所示。
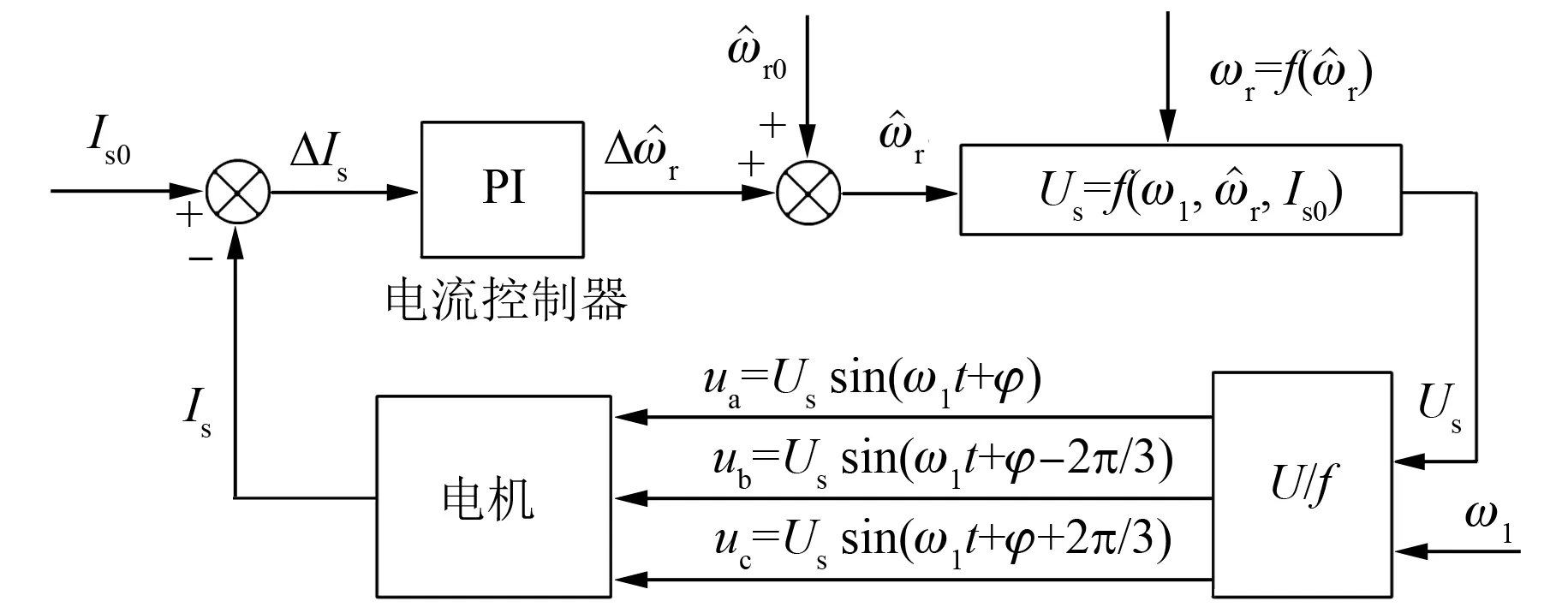
图3 控制系统结构框图

图4 控制系统被控对象传递函数方块图
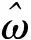
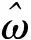

图5 不同的fs时,Is-Is0与r之间的关系曲线
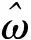
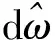
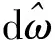
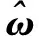
表3 不同输出角频率ω1对应的估计转速r值


(9)
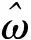
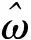
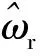
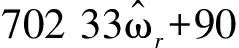
(10)
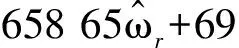
(11)
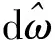
将式(9)~式(11)整合成分段函数的形式:
(12)
2. 3 控制器参数设计
由于本文的理论分析是基于稳态下的数学模型建立,故无法直接得到被控对象的传递函数来进行控制器参数设计。为此采用工程的方法测定被控对象能否等效为一个低阶系统,从而对控制系统进行简化,设计合理的控制器参数。
通常以单位阶跃响应来讨论控制系统的瞬态性能指标,故可以给被控对象输入端一个阶跃信号,观察开环系统的阶跃响应曲线来确定被控对象是否可简化成低阶系统。具体做法如下:
给被控对象G(s)输入端一个阶跃信号r(t)=0.5×2π/G(0)(t),则相当于给G′(s)输入端相同大小r′(t)=0.5×2π(t)的阶跃信号,观察开环系统的定子电流Is阶跃响应曲线。某一工况下的定子电流阶跃响应曲线如图6所示。

图6 定子电流Is阶跃响应曲线
由图6的阶跃响应曲线可见,被控对象传递函数G′(s)可以看成是一个二阶的系统。表4列出了不同工况下测得的二阶系统的瞬态性能指标。
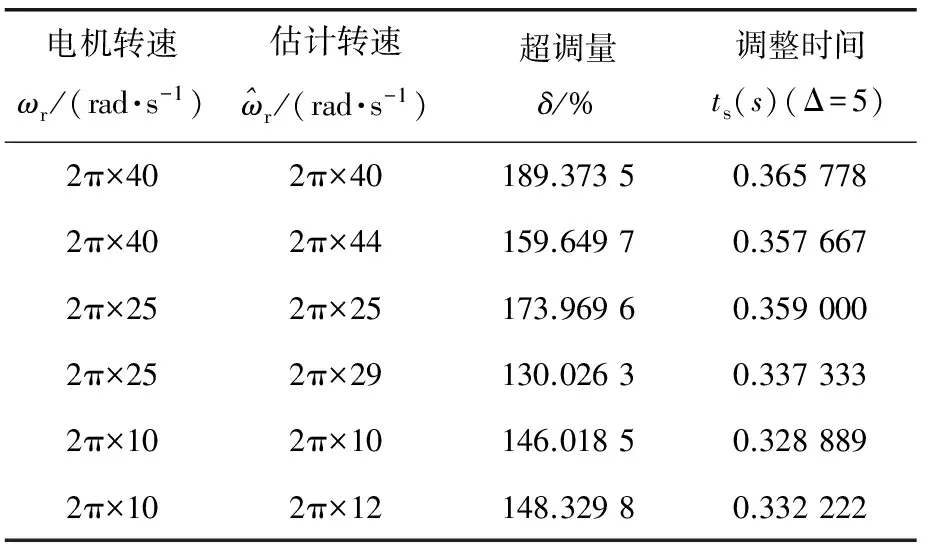
表4 不同工况下测得的二阶系统瞬态性能指标
由表4可见,不同工况下测得的瞬态性能指标相差不大,选取最恶劣的数据作为G′(s)可以等效为的二阶系统瞬态性能指标,即δ=189.373 5%,ts=0.365 778 s,可得出G′(s)可以等效为的二阶环节传递函数如下:
(13)
式中:ζ=0.199 184,ωn=41.176 481。根据式(13)可以得到对数幅值为-3 dB时对应的带宽频率ωc=62.2 rad/s。
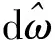
(14)
为了保证在参数设计时,可以将控制系统内环传递函数G′(s)等效为1,且避免过快的动态过程对转速估计的影响,闭环系统带宽频率KiG(0)设置为G′(s)带宽频率ωc的1/10,即
(15)
求得Ki≤17.804 7。
3 仿真验证
本文的MATLAB/Simullink仿真所采用的变频器主电路拓扑为主流的级联H桥多电平结构[10]。三相异步电机的模型参数如表1所示。
首先按照文献[8]的方法进行仿真,若不减慢ω1下降速率,仿真结果波形如图7所示。2.257 s输出角频率ω1等于电机转速ωr,但由于此时定子电压幅值Us达不到恒定磁通U/f曲线上对应的电压(3 525 V),搜索频率失败,此后电流控制器无法控制电流且能量反灌会导致直流侧过压。若采取减慢ω1下降速率的方法,虽然可以搜到频率,但是搜索频率时间较长,无法满足实际搜索频率要求。

图7 文献[4]搜索转子频率控制结果
当电机反电动势衰减到10%以下,即可认为其已衰减到接近于零时,可以采用本文的方法搜索电机转子频率,PI控制器参数Ki取为17。
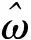
具体仿真过程如下:本文的仿真在t0=1 s电机处于额定运行状态,电机转速为314 rad/s;t1=2 s封闭PWM脉冲;t2=7 s开起PWM脉冲;7~7.5 s指令电压Us从0开始增加到Us0;t3=7.5 s开始搜索电机转子频率,定子电流幅值、转速的波形如图8所示。
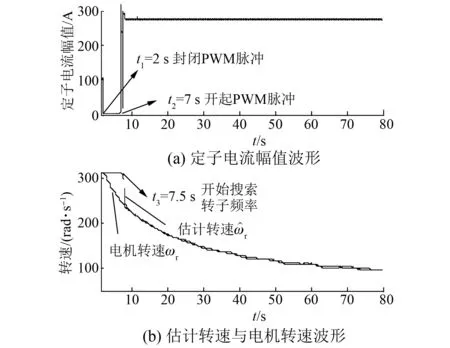
图8 转子频率搜索仿真波形
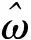
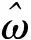
图9、图10分别为8.2 s、80 s时刻拖动电机运行到额定转速的高压变频器“飞车起动”仿真波形。

图9 8.2 s“飞车起动”仿真波形

图10 80 s“飞车起动”仿真波形
4 结 语
鉴于大多数文献的转子频率搜索方法普遍存在搜索速度慢、搜索精度低、适用范围有局限性、控制算法复杂等问题,提出了一种新型的电机转子频率搜索算法,无需配置电压互感器和速度传感器,算法仅通过检测和控制定子电流的幅值即可获得电机转子频率。
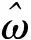
[1] 罗德荣,王耀南,葛照强,等.级联型高压变频器控制算法的研究及实现[J].电工技术学报,2010,25(1): 104-110.
[2] 郭立,陈远华,刘文华,等.高压变频器的起动及瞬时停电控制[J].电力电子技术,2006,40(2): 25-27.
[3] 白德芳.高压变频器“飞车启动”功能的实现[C]∥ 中国高校电力电子与电力传动学术年会,2007: 74-79.
[4] 宋瑞智,刘贺平,赵敏.高压变频器瞬时停电再起动方法的MATLAB仿真[J].电机与控制应用,2010,37(8): 54-58.
[5] CHOI S C, LEE J, HONG C, et al. Restarting strategy for an induction machine driven with medium-voltage inverter[C]∥ 9th International Conference on Power Electronics-ECCE Asia, 2015: 1881-1888.
[6] HARNEFORS L, HINKKANEN M. Stabilization methods for sensorless induction motor drives—a survey[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics, 2014, 2(2): 132-142.
[7] 李永东,李明才.感应电机高性能无速度传感器控制系统——回顾、现状与展望[J].电气传动,2004,34(1): 4-10.
[8] PAN H W, LOTHAR S, JOANCHIM H. Improving the start and restart behavior through state recognition of AC drives[C]∥ Proceedings of the Power Conversion Conference-Nagaoka, 1997: 589-594.
[9] 陈伯时.电力拖动自动控制系统[M].3版.北京: 机械工业出版社,2003.
[10] TOLBERT L M, PENG F Z, HABETLER T G. Multilevel converters for large electric drives[J]. IEEE Trans on Industry Applications, 1999, 35(1): 36-44.
A New Method of Searching Rotor Speed*
HUWenhao1,WUZhenxing1,SUNLe2,CAIXinjian3
(1. National Key Laboratory for Vessel Integrated Power System Technology, Naval University of Engineering, Wuhan 430033, China; 2. School of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 3. School of Electrical Engineering, Huazhong University of Science and Technology, Wuhan 430074, China)
A new method of searching rotor speed without voltage or speed sensor was proposed. The method searched the rotor speed according to the magnitude of the stator current. The steady-state mathematical expression between the stator voltage, the output frequency and the rotor speed was deduced which kept the stator current constant. Then the monotonicity between the current magnitude and the estimated speed under the certain conditions could be found. A searching strategy of changing the output frequency according to the given laws was proposed, which improved the rapidity and the accuracy of the searching process. The simulations verified that the theoretical analysis and the proposed method were correct and effective.
rotor speed search; high-voltage inverter; flying start; asynchronous motor
国家自然科学基金(51477179);国家高技术研究发展863计划(2013AA050404)
胡文豪(1990—),男,硕士研究生,研究方向为电力电子及电力传动。
TM 301.2
A
1673-6540(2017)04- 0006- 08
2016 -09 -20

