基于二阶滑模算法的无刷直流电机转速控制研究
王君力, 张安堂, 张 颖, 倪 磊
(空军工程大学 防空反导学院,陕西 西安 710051)
基于二阶滑模算法的无刷直流电机转速控制研究
王君力, 张安堂, 张 颖, 倪 磊
(空军工程大学 防空反导学院,陕西 西安 710051)
研究了二阶滑模控制方法,将其引入无刷直流电机调速系统中。根据螺旋算法控制规律,设计了滑模控制器,使电机能够跟踪位置指令,快速响应转速调节。二阶滑模能够规避传统滑模的抖振现象,并且可以改善电机调速系统抗外界干扰的能力。仿真和试验结果表明,提出的方法可以使电机输出转速动态响应快,调节时间短,稳定匀速运行,验证了文中理论分析的正确性与有效性。
无刷直流电机; 转速控制; 二阶滑模; 螺旋算法
0 引 言
无刷直流电机(Brushless DC Motor,BLDCM)作为一种机电一体化新型产品,具有效率高、控制简单、结构稳定、功率密度大等优点,在工业控制、航空航天等领域都得到了广泛应用[1]。电机调速性能[2-9〗的改善长期以来都是众多专家学者的重点研究内容之一,高精度的伺服控制要求电机不仅能够对指定位置角实现精确稳定跟踪,而且其动态响应时间要短,并具有一定抗扰动能力,即电机在有限的时间内能够快速准确地输出指定转速,且不受外界负载扰动的影响。
目前,BLDCM多采用PI算法实现速度环的调节。随着控制理论的快速发展,越来越多先进控制方法被应用到电机调速系统。文献[2]提出了一种神经网络逆控制器的设计方法,很大程度上弱化了参数变动等非线性因素的影响,从而改善了电机的调速性能;文献[3]提出了改进单神经元自适应PID控制方法,实现了对比例系数K的在线自适应调节,极大地提升了电机速度调节器的品质。上述研究提升了电机转速调节的鲁棒性,却没有考虑电机转速调节响应时间。文献[4]提出了一种新型二阶滑模观测器,不需要低通滤波器就能够消除滑模抖振现象,用其估计电机转子位置和速度,可以改善系统鲁棒性和观测精度。
当运行中的伺服系统出现负载扰动及参数变化等情况时,其自身控制性能会受到影响,转速的控制精度不高,进而影响电机的位置跟踪和动态响应。为解决上述问题,本文选用高阶滑模算法中的二阶滑模[10-16〗对电机速度环进行控制,基于螺旋算法,以绕组电流作为控制量,使电机能够迅速完成加速过程,输出期望转速,对给定位置角指令实现快速跟踪。同时,由于二阶滑模算法具有对负载及参数变化不敏感的特点,有利于提高伺服系统的抗干扰能力。本文从改善电机转速响应和稳定匀速运行两个方面进行研究,提出的控制方法有助于改善电机转速调节的动态特性。
1 BLDCM数学模型
数学模型是对BLDCM驱动控制系统进行设计的理论基础。为方便建立电机的数学模型,假设以下条件成立:
(1) 电机定子绕组产生的反电动势波形是平顶宽度120°电角度的梯形波;
(2) 忽略磁路饱和,不考虑涡流和磁滞损耗;
(3) 三相定子绕组分布均匀,忽略齿槽效应。
图1所示为BLDCM等效电路图。图1中Si(i=1…6)表示6个功率开关管,ia、ib、ic分别表示绕组相电流,r表示绕组等效电阻,LM表示绕组自感与绕组间互感之差,ea、eb、ec分别表示绕组相反电动势,基于此对电机数学模型做以下分析。

图1 BLDCM等效电路图
直流电源给电机伺服系统提供能量,除小部分损耗外,大部分转换为力矩作用于电机转子。这部分能量称为电磁功率,其值相当于三相绕组反电动势与相电流乘积求和,即:
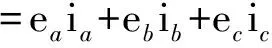
(1)
式中:Pe——电磁功率;Te——电磁转矩;ω——电机角速度。
引入负载转矩TL、转子转动惯量J、粘滞摩擦因数Bv,可得电机的机械运动方程为
(2)
2 BLDCM转速环的二阶滑模控制
2. 1 二阶滑模
滑模变结构控制算法是一种非线性控制策略,对外部扰动及参数变化不敏感,具有很强的鲁棒性,并且控制算法相对简单,便于工程应用与实践,故在电机控制领域得到了广泛应用。传统滑模控制存在抖振的现象,近年来提出的高阶滑模控制,不仅保留了传统滑模控制既有的优点,而且也消除了抖振现象。其将开关切换作用在滑模变量的高阶导数上,相当于利用一个连续的控制量(不存在切换作用)使滑模变量趋近于零,在高精度控制领域有很大应用潜力。
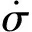
设单输入非线性系统:
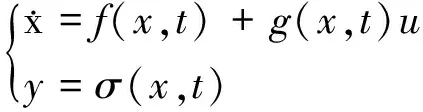
(3)
式中:x——状态变量;f、g——未知的光滑函数;u——有界连续的控制量;σ——输出函数即滑模变量。
考虑到二阶滑模控制的目标,使控制系统稳定,对滑模变量求两次导,可得
(4)
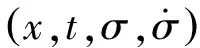
(5)

2. 2 滑模控制器设计
螺旋算法是二阶滑模控制中最简单的算法。其控制量的具体形式如下:
(6)
在有限时间内,滑模变量σ(x,t)收敛的充分条件为
(7)

结合BLDCM的机械运动方程,参考式(3)建立如下方程:
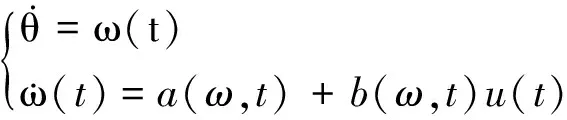
(8)
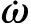

对定义的滑模变量分别求一次和两次导数,可得
(9)
(10)
由式(9)可知,该二阶滑模控制系统相对阶数是1。式(10)中A=A0+ΔA,A0表示电机已知标称值构成的表达式,ΔA表示参数变动及外界扰动给系统带来的不确定性。这里的负载转矩TL是一个复合的概念,包括阻尼转矩和各种扰动转矩(比如齿槽转矩、传感器误差、电源波动,以及电机参数变化造成的转矩扰动)。
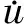

(11)
式中,α>0表示控制增益,由r1=3α,r2=α,参考式(7)进一步得到:
(12)
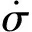
现定义Lyapunov函数为
(13)
由式(4)、式(5)和式(11)可得
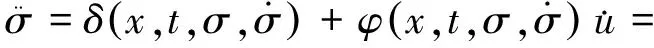

(14)
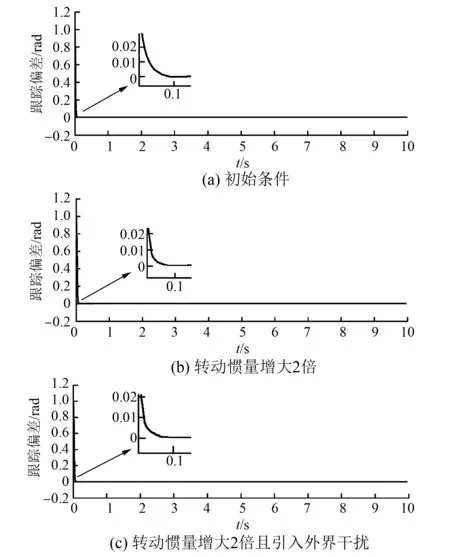
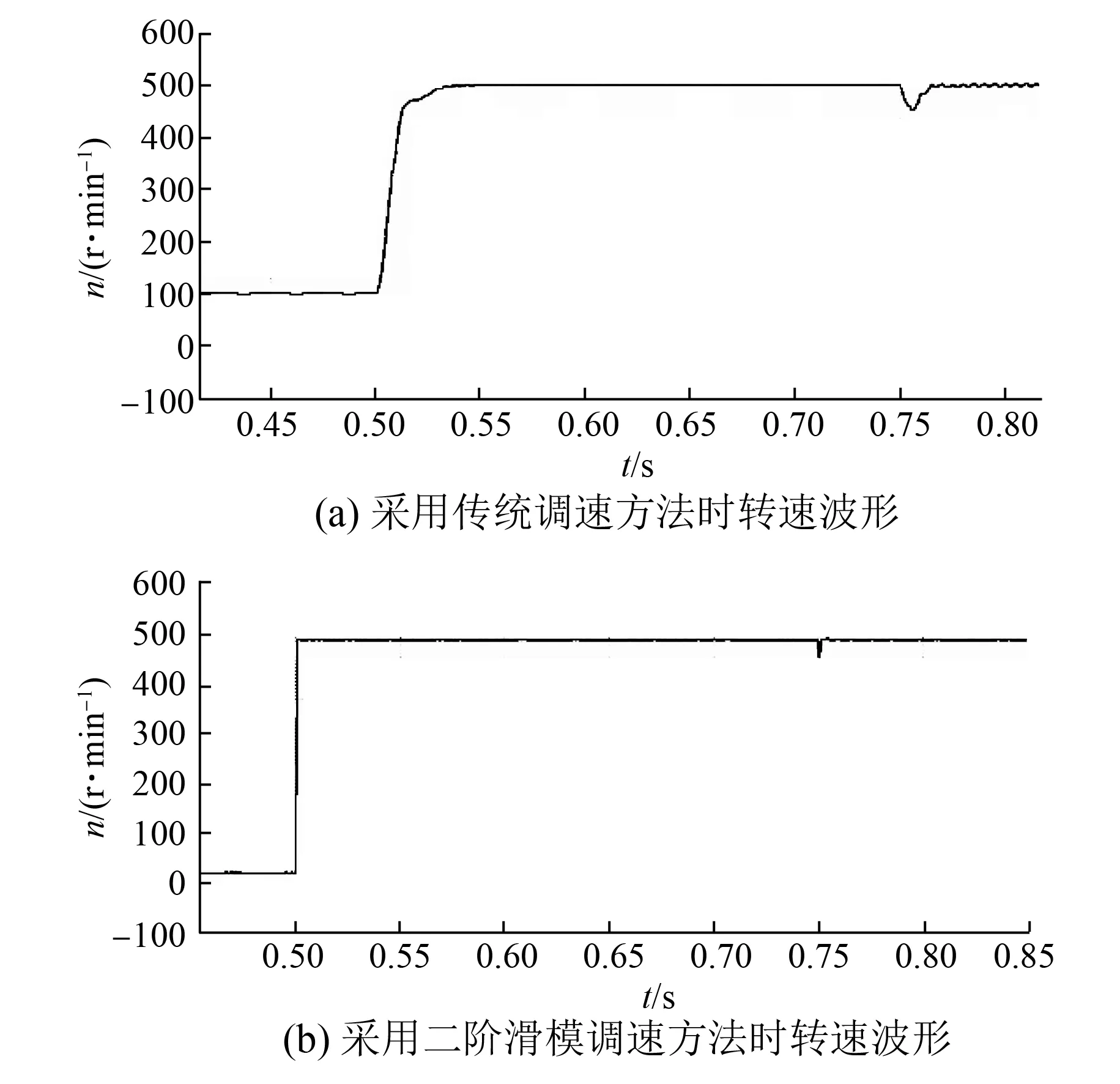
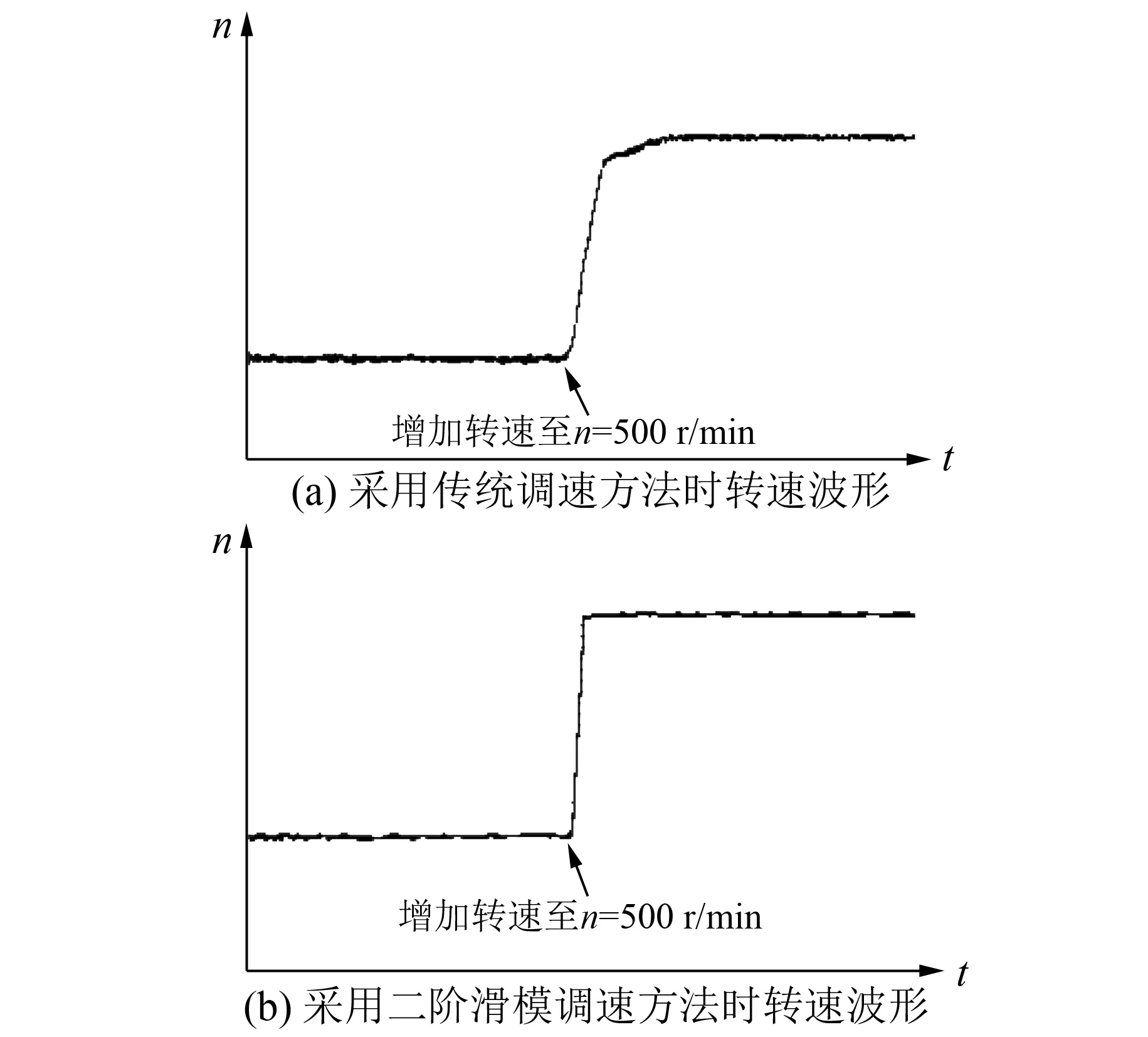
式中: 0 则对V(t)求导得 (15) 由式(12)可知: 则有: (16) 根据以上分析研究,可得到基于二阶滑模控制算法的电机速度环控制结构图如图2所示。 图2 基于二阶滑模控制算法的速度环控制结构图 利用传感器检测电机转子速度信息ω,积分可得位置角信息θ,与参考位置角θref比较作差得到误差信号e,基于螺旋算法控制律,经过二阶滑模控制算法运算处理输出控制量u,即绕组电流值i,作为参考电流进入转矩控制环节。采用二阶滑模控制算法能够快速响应转速调节,跟踪位置指令,并且能抑制外界扰动TL对电机的干扰,使电机稳定运行,改善BLDCM伺服系统速度环的控制性能。 3. 1 仿真验证 图3 位置及转速跟踪波形 如图3所示,电机位置角在很短时间内良好地跟踪了参考指令,输出转速动态响应快;从跟踪偏差图4可得,尽管电机在运行过程中受到外界干扰,甚至其自身参数也发生了较大变化,但是跟踪误差并没有出现明显波动,凸显了二阶滑模算法的优势。图5滑模变量的相轨迹表明螺旋算法控制律的特点。 为了进一步验证滑模控制的合理性,将其作为转速控制方法引入BLDCM伺服系统中,与传统控制方法对比分析,电机初始转速设定为100 r/min,在t=0.5 s时,输入单位阶跃信号提高电机转速至500 r/min,在t=0.75 s时施加负载转矩。仿真波形如图6~图7所示。 图4 跟踪偏差波形 图5 滑模变量σ相轨迹 图6 无刷直流电机转速波形 图7 负载转矩TL=2 N·m时转速波形 给定转速是阶跃信号,如图6所示。采用本文提出的转速控制方法,当t=0.51 s时,电机转速就达到了稳定值n=500 r/min,相比传统控制方法,其转速响应时间(t=0.55 s时转速趋于稳定)更短。这表明采用二阶滑模控制电机转速,可以改善系统的动态响应性能,实现电机转速的快速调节。 如图7所示,电机运行转速稳定在500 r/min,当t=0.75 s时,突加负载扰动转矩TL=2 N·m。相比传统控制方法,采用二阶滑模转速控制方法可以在很短时间内稳定电机转速,有效抑制负载转矩给电机调速系统所带来的外界干扰,表明该系统具有比较强的鲁棒性,验证了二阶滑模控制算法的特点与优势。 3. 2 试验验证 为对本文所提出的理论进行验证,以DSP2812为控制器搭建了一个试验平台。由于在试验调试过程中转速响应时间相对于整个试验过程很短,故对示波器采集的波形做了适当的放大处理。试验中通过精确控制磁粉制动器的转矩输出,模拟外界施加负载扰动转矩。 图8为采用不同调速方法得到的电机转速响应波形。与传统转速控制方法相比,本文提出的二阶滑模转速控制方法能明显减小电机转速响应时间,与仿真结果一致,即系统具有更好的动态响应性能。 图8 无刷直流电机转速波形 如图9所示,相比传统调速方法,采用二阶滑模转速控制方法得到的试验结果比较理想,能更好地抑制外界干扰对电机稳定运行的不利影响。图8~图9中电机的转速波形是利用DSP自带的D/A输出端口经RIGOL数字示波器采集得到,其模拟输出波形虽然有毛刺,但并不影响试验观测,波形整体趋势仍能反映转速的变化情况。 图9 负载转矩TL=2 N·m时转速波形 二阶滑模算法不仅具有传统一阶滑模控制的优点,而且有效规避了抖振现象,同时又便于工程应用的实现。本文将二阶滑模算法引入BLDCM调速系统中,基于螺旋算法控制律,把绕组电流定义为系统的控制量,相比传统控制方法,明显缩短了转速的动态响应时间,并且使系统的鲁棒性更强,保证了电机的稳定运行。仿真与试验结果表明,本文提出的方法能有效改善电机转速控制性能。 [1] 夏长亮,方红伟.永磁无刷直流电机及其控制[J].电工技术学报,2012,27(3): 25-34. [2] 刘国海,金鹏.无刷直流电机调速系统神经网络逆控制[J].电工技术学报,2010,25(8): 24-30. [3] 王秀君,胡协和.一种改进的单神经元PID控制策略[J].浙江大学学报(工学版),2011,45(8): 1498-1501. [4] 刘江.基于二阶滑模观测器的永磁同步电动机无传感器控制[J].微特电机,2015,43(8): 65-72. [5] 王少威,万山明.基于最小拍无纹波数字化的PMSM速度调节器[J].华中科技大学学报(自然科学版),2011,39(9): 121-124. [6] 汪俊杰,周波.基于前馈控制的BLDCM滑模变结构调速系统[J].电工技术学报,2008,23(8): 41-46. [7] 夏长亮,李志强.无刷直流电机小脑模型网络与PID复合控制[J].电机与控制学报,2008,12(3): 254-259. [8] 李浩然,杨旭红,薛阳,等.基于模糊PI参数自整定和重复控制的三相逆变器并网研究[J].电机与控制应用,2015,42(2): 31-36. [9] 王同旭,马鸿雁.电梯用永磁同步电机BP神经网络PID调速控制方法研究[J].电工技术学报,2015,30(1): 43-47. [10] 史婷娜,马银银.基于二阶滑模观测器的无刷直流电机转子位置估计[J].天津大学学报(自然科学与工程技术版),2014,47(8): 697-702. [11] 郭鸿浩,周波.永磁无刷直流电机角加速度估计[J].电工技术学报,2014,29(5): 93-103. [12] 文小飞,万俊,席世友,等.不平衡电网条件下DFIG滑模变结构直接功率控制[J].电机与控制应用,2015,42(4): 21-26. [13] LIU G, ZHANG C. Sliding mode control of reaction flywheel-based brushless DC motor with buck converter[J]. Chinese Journal of Aeronautics, 2013, 26(4): 967-975. [14] 史婷娜,张茜.无刷直流电机反电势滑模观测及参数在线辨识[J].兵工学报,2013,34(6): 739-747. [15] 李政,胡广大.永磁同步电机调速系统的积分型滑模变结构控制[J].中国电机工程学报,2014,34(3): 431-437. [16] 侯利民,王巍.表面式永磁同步电机无源非奇异快速终端滑模控制[J].电工技术学报,2014,29(11): 45-52. Research on Speed Control of Brushless DC Motor Based on Second-Order Sliding Mode WANGJunli,ZHANGAntang,ZHANGYing,NILei (College of Air and Missile Defense, Air Force Engineering University, Xi’an 710051, China) Second-order sliding mode was proposed to design the speed controller system of brushless DC motor(BLDCM), and its controller was established based on twisting algorithm to track position command and adjust speed. Furthermore, the chattering problem of traditional sliding mode could be eliminated by using second-order sliding mode, which also reduced outside disturbances, improving the speed control performance of servo system. Simulation and experimental results showed that the method was presented which could keep the dynamic response quick, shorten settling time and run at constant speed stably. And the validity and corrective of the theoretical analysis were verified in the end. brushless DC motor (BLDCM); speed control; second-order sliding mode; twisting algorithm 王君力(1991—),男,硕士研究生,研究方向为交流伺服技术。 张安堂(1960—),男,副教授,研究方向为电力电子变换、交流伺服技术。 TM 301.2 A 1673-6540(2017)04- 0080- 06 2016 -07 -11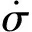
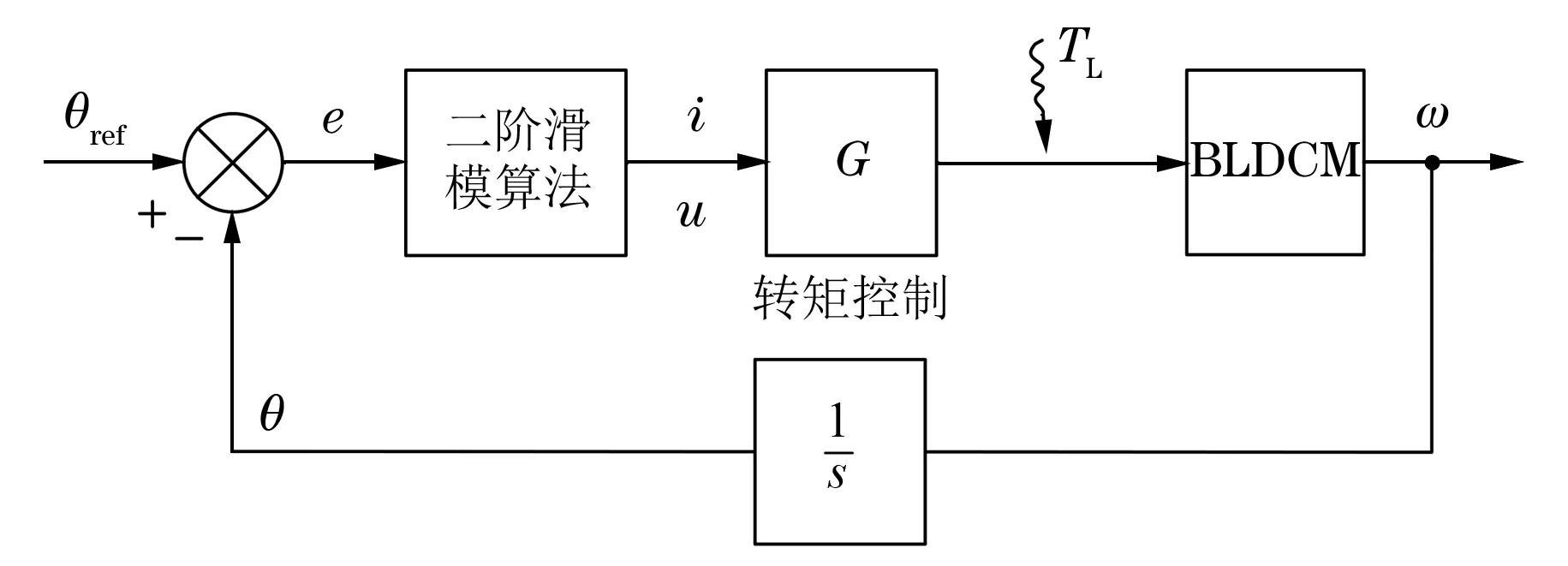
3 仿真与试验验证
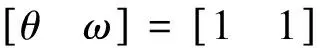




4 结 语

