太阳系行星际航天器外热流计算方法研究

刘 洋，彭晓东，张汉勋，郭 颂，明 星

（1.中国科学院国家空间科学中心 北京 100190；2.中国科学院大学 北京100049；3.中国科学院光电研究院 北京 100094）

太阳系行星际航天器外热流计算方法研究

刘 洋1，2，彭晓东1，张汉勋1，郭 颂1，2，明 星3

（1.中国科学院国家空间科学中心 北京 100190；2.中国科学院大学 北京100049；3.中国科学院光电研究院 北京 100094）

针对传统国内外热流算法以及某些国外商业软件只计算单行星轨道航天器外热流的不足，提出了太阳系行星际轨道航天器的外热流计算方案。本文方案采用积分定义法，平行光线法，近似法，插值法，考虑行星椭圆轨道的影响以及面元遮挡。仿真计算结果表明，该方案符合行星际轨道外热流物理特性，其计算效率和精度较高。

外热流；角系数；行星际轨道；航天器；辐射换热

外热流计算是航天器热分析和热设计的前提，目前外热流计算主要采用Monte Carlo法（MC法）和积分法[1]。文献[2]采用积分法计算了平板的太阳辐射角系数，地球红外辐射角系数以及地球反照角系数，被文献[3]等作为在无遮挡状况下的标准计算值。文献[3]采用MC法计算任意凸面物体所受的外热流；文献 [4]提出采用MC法求解凹面和可视面的外热流；文献[1]采用均匀分布法求解外热流；另外还有通过坐标变换和矢量计算求解外热流的方法。

这些文献和方法均为地球轨道卫星的外热流计算，考虑了太阳辐射和地球对航天器空间外热流的影响。目前大多数国内文献以及传统算法只考虑单星球轨道航天器的外热流，其中地球卫星的外热流计算研究最多，没有对行星际轨道航天器外热流计算方法进行研究和分析。国外热分析软件进行了单星轨道卫星的热分析，比如Thermal Desktop软件，只对各大行星以及月球单星轨道卫星进行热分析，且计算过程中未考虑行星位于椭圆运行轨道不同位置对其太阳常数的实时影响，只以经验常数代替，这对于近日行星卫星外热流计算会产生一些误差。

文中针对传统研究的以上待研究处，考虑太阳实际远近距离对计算的影响以及除地球外其他行星和行星自然卫星的影响，并且考虑遮挡因素，平衡算法的精度和效率，开展了太阳系行星际航天器外热流计算方法的研究，总结出行星际轨道航天器的外热流计算方案，并进行仿真计算。

1 外热流计算方法

地球轨道卫星外热流主要由太阳辐射外热流、地球的红外辐射外热流和反照辐射外热流构成[3]。地球轨道卫星面元i的外热流Qei公式为：

对于太阳系行星际轨道航天器外热流，主要由太阳辐射外热流、各行星以及行星自然卫星的红外辐射外热流和反照辐射外热流构成。面元i的外热流Qi公式为：

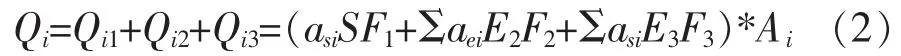
其中：Qi1为太阳辐射外热流，Qi2为各行星及行星自然卫星的红外辐射外热流，Qi3为各行星及行星自然卫星的反照辐射外热流。asi，aei分别为航天器面元i的太阳辐射吸收率和表面红外发射率，是与航天器材质有关的常数。Ai为面元i的面积。S，E2，E3分别为太阳常数，各行星以及行星自然卫星红外辐射密度，各行星以及行星自然卫星反照辐射密度，单位为W/m2。F1，F2，F3分别为太阳辐射角系数，各行星以及行星自然卫星红外辐射角系数，各行星以及行星自然卫星反照辐射角系数。行星际航天器外热流的计算主要为这6个参数的计算。其中，关键是F1，F2，F3的计算方法。

1.1 航天器模型与互视遮挡判断

文中采用离散网格表示航天器各表面，建立航天器的三维模型，进行三角面片划分，提取三角面片信息，作为外热流计算的输入，再通过规则网格划分将模型重新解析，以方便遮挡的计算。首先对航天器面片进行一次外层面片和一次互视判断，保存结果；有互视的面片才有可能相互遮挡，故只对有互视的面片在外热流计算值大于零的情况下计算遮挡。

1.2 S，E2，E3的计算

关于S的计算。跟据斯蒂芬—玻尔兹曼定律，σ为斯蒂芬—玻尔兹曼常数，取太阳表面有效温度TS为5 766 K，则太阳的辐射力为：σT4s（W/m2）[2]。以往文献中S均为地球附近太阳常数，取经验值1 353 W/ m2，这里我们取S为太阳附近太阳常数（因为F1的计算方法也不同），即：

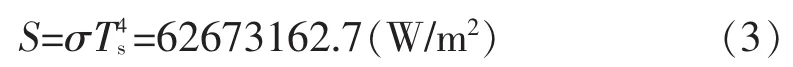
关于各行星以及行星自然卫星E2，E3的计算，不同星体计算方法相同。

其中，ρ为各行星以及行星自然卫星对太阳辐射的平均反射率；Se为各行星以及行星自然卫星附近太阳常数，Se=62 673 162.7*（R/d）2，R为太阳半径，d为各行星以及行星自然卫星到太阳的距离。

传统计算方法计算地球轨道卫星外热流时，取日地平均距离处的E2、E3常数。然而对于行星际轨道航天器，各行星以及行星自然卫星运行轨道为椭圆轨道，与太阳的距离实时改变，某些行星近日距离和远日距离相差较大，计算所得的E2、E3也相差较大，以往取平均距离计算的E2、E3常数，对外热流计算带来相当大的误差，尤其是对于近日行星。

表1列出了各行星近日点，远日点，平均距日距离下E2、E3的值，比较可以看出，对于金星，地球，火星，近日点，远日点的E2、E3相差十W/m2左右。对于水星，近日点，远日点的E2相差高达千W/m2，E3相差百W/m2。故文中用实时距离计算E2、E3，可避免由此带来的计算误差。

表1 各行星近日点，远日点，平均距日距离下E2、E3比较

1.3 角系数计算

1.3.1 太阳辐射角系数F1的计算

在距离太阳一定远时，太阳辐射密度衰减为小于10 W/m2或1 W/m2或更小时，我们认为此范围的航天器太阳辐射外热流为零，记航天器的这个高度为极限高度。

在极限高度范围内，当航天器距离太阳足够近时，F1计算用积分法，我们称这个高度为F1分界高度；当高度超过F1分界高度时把太阳光看成平行光，用平行光法，即

式中βs为太阳光与航天器面元法线的夹角，Rs为太阳半径，d为航天器面元到太阳的距离。

极限高度和分界高度的计算可根据精度做调整。选误差小于1 W/m2，则有极限高度为5 505 326 470 km，约为7 915个太阳半径。选误差小于0.2 W/m2，则有分界高度为22 000 000km，约为32个太阳半径。

1.3.2 各行星以及行星自然卫星红外辐射角系数F2的计算

对于不同行星以及行星自然卫星，F2计算方法相同，只是各星球参数不同。由于各行星以及行星自然卫星红外辐射和太阳辐射均为电磁波辐射，故F2与F1计算方法类似。

对于不同行星以及行星自然卫星，统称为星体。在距离星体一定远时，星体红外辐射密度衰减为小于10 W/m2或1 W/m2或更小时，认为此范围航天器受此星体红外辐射外热流为零，记航天器的这个高度为极限高度。

在极限高度范围内，航天器距离星体足够近时，F2计算用文献[2]中积分法，称这个高度为F2分界高度；超过F2分界高度时把星体辐射看成平行光，用平行光法，即

式中β为星体与面元连线与航天器面元法线的夹角，R为星体半径，d为航天器面元到星体的距离。

极限高度和分界高度的计算可根据精度做调整。以水星为例，在平均距日距离下，选误差小于1 W/m2，则有极限高度为110 561 km，约为45.33个水星半径；有F2分界高度为13 500 km，约为5.54个水星半径。

1.3.3 各行星以及行星自然卫星反照角系数F3的计算

由于F3积分限复杂，影响因素多，计算复杂，对于不同行星以及行星自然卫星，其参数，包括距日距离，半径，对太阳辐射的反射率等不同，故在不影响精度的情况下，对不同行星以及行星自然卫星采用不同的方法进行计算，提高计算效率。

同样，对于不同行星以及行星自然卫星，在距离星体一定远时，星体反照辐射密度衰减为小于10 W/m2或1 W/m2或更小时，认为此范围航天器受此星体反照辐射外热流为零，记航天器的这个高度为极限高度。

在极限高度范围内，航天器距离星体足够近时，F3计算用文献[2]中积分法，我们称这个高度为F3分界高度；超过F3分界高度时用近似法，即：

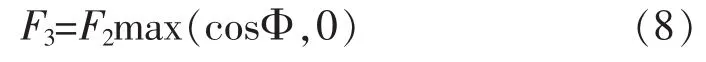
Φ为面元和星体连线与太阳和星体连线的夹角，max（）求括号中参数的最大值。

用积分法计算F3时，影响F3的因素多，积分区域复杂，计算效率低，在不影响精度情况下，近似计算是必要的[2]。对于F3的计算，和F2计算相关，影响参数增加了Φ，即面元和星体连线与太阳和星体连线的夹角，故近似法采用公式（8）。对于地球F3，根据文献[2]，近似法计算误差在允许范围内。

极限高度和分界高度的计算可根据精度做调整。以地球为例，在平均距日距离下，选误差小于1 W/m2，则有极限高度为133 602 km，约为20.88个地球半径；选误差小于4 W/m2，有F3分界高度为30 000 km，约为4.69个地球半径。

另外，对于地球和金星，其半径相差很小，在极限高度范围内，计算影响参数，根据文献[2]中积分法F3表，用查表插值法计算F3，以提高计算效率。

1.3.4 遮挡问题

关于遮挡的问题，在面元外热流计算值大于零的情况下计算遮挡比。从航天器三角面元三顶点及重心发射4条光线，用光线追踪法计算遮挡比。然后用此面元求得的外热流值乘以未遮挡比作为此面元外热流结果值。

2 方案总结与计算结果分析

表2总结了太阳系行星际轨道航天器外热流的计算方案。

表3列出了航天器面元外热流计算考虑的部分星体的一些参数。对于不考虑计算的星体以及原因如下。根据计算数据，冥王星距离太阳太远，附近太阳常数极小，约0.9 W/m2，其红外辐射平均密度和反照辐射密度不到0.2 W/m2，可忽略不计。水星，金星没有自然卫星，木星之外行星自然卫星距离太阳远，可忽略不计算。火星的两颗自然卫星形状不是规则球体，太阳常数相对较小，也可不计算，或视情况定。故对于行星自然卫星，只计算地球的自然卫星月球对航天器面元外热流的影响。

从表3可知，航天器在太阳系中所受外热流组成由其位置决定。在太阳辐射极限高度范围内，没有行星的遮挡情况下，航天器外热流主要是太阳辐射外热流。在靠近某一行星，进入其极限高度后，才受这一行星的红外辐射和反照辐射的影响。经计算，各行星以及地球卫星月球对航天器外热流计算的影响范围没有交集。

表2 方案总结

表3 星体相关参数

图1为用平行光法计算太阳辐射外热流的绝对误差。其中不同的线条代表了不同的β角，不同β角的误差有一些差别，为了不失普遍性从0度到180度等间隔取8个角度，横坐标为卫星面元距离太阳表面的高度，纵坐标为平行光法计算的绝对误差，单位为W/m2。从图中可以看到，随航天器高度升高，计算误差有降低的趋势。当航天器高度超过22 000 000 km，约为32个太阳半径，平行光法计算误差小于0.2W/m2。本文方案，当航天器高度小于22 000 000 km，则用积分法。故本方案计算太阳辐射外热流误差小于0.2W/m2。

图1 太阳辐射外热流平行光法计算绝对误差

对于星体红外辐射外热流计算误差，以金星为例，图2为用平行光法计算平均距日距离下金星红外辐射外热流的绝对误差。其中不同的线条代表了不同的β角，从0度到180度等间隔取8个角度，横坐标为航天器面元距离金星表面的高度，纵坐标为平行光法计算的绝对误差，单位为W/m2。从图中可以看到，随航天器高度升高，计算误差有降低的趋势。当航天器高度超过13 200 km，约2.18个金星半径，平行光法计算误差小于1 W/m2。本文方案，当航天器高度小于13 200 km，则选用文献[2]中的积分法。本方案误差小于1 W/m2，绝大部分计算值相对误差小于3%，个别点如β在特殊角度如90度左右时相对误差较大，但绝对误差很小，小于1 W/m2。文献[3]中MC算法相对误差小于3%。然而文献[3]中MC算法发射100 000条光线用于计算，效率低，本方案综合考虑效率和精度问题，在个别点的计算上相对误差虽大，但绝对误差很小，且用本方案的方法不需要发射大量的光线进行计算，在误差允许的范围内，提高了效率。

对于星体反照辐射外热流计算误差，以地球为例，图3为用近似法计算平均距日距离下地球反照辐射外热流误差。其中不同的线条代表了不同的Φ，横坐标为航天器面元距离地球表面的高度，纵坐标为近似法计算的绝对误差，单位为W/m2。此外，还有许多影响反照辐射外热流计算的其他因素，如面片法线与面片地球连线夹角等，我们取这些值使得计算产生最大的误差。从图中可以看到，计算误差随航天器高度升高，有先升高后降低的趋势，其最大误差约为20 W/m2。当航天器高度超过30 000 km，约4.69个地球半径，近似法计算误差小于4 W/m2。本文方案，当航天器高度小于30 000 km，则选用文献[2]中的积分法。本方案误差小于4 W/m2，绝大部分计算值相对误差小于3%，个别点如Φ在特殊角度90度左右时相对误差较大，但绝对误差很小，小于4W/m2。

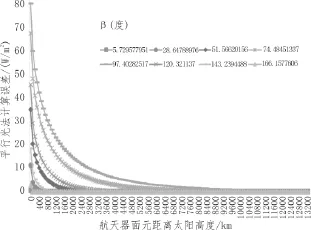
图2 平均距日距离下金星红外辐射外热流平行光法计算绝对误差

图3 平均距日距离下地球反照辐射外热流近似法计算绝对误差

此方案在计算时，当外热流计算值大于零时，计算遮挡比，某些情况下需要积分计算，综合来看，本方案效率较高。

3 结 论

文中给出了太阳系行星际轨道航天器外热流计算方案，由定义以及计算结果验证了其正确性，且效率和精度均较高。计算方法采用了积分法，平行光线法，近似法，插值法，考虑了面片的遮挡计算和行星际星体实际位置关系对计算的影响。计算中判断一次外层面片，一次互视，做标记；用效率高，准确率高的方法计算外热流，大于零，才做遮挡判断，从而提高了计算效率。

[1]张涛,孙冰.计算近地轨道航天器空间外热流的RUD方法[J].宇航学报，2009（1）:338-343.

[2]杨贤荣，马庆芳，等.辐射换热角系数手册[M].北京:国防工业出版社，1982.

[3]翁建华，潘增富，闵桂荣.空间任意凸面的轨道空间外热流计算方法[J].中国空间科学技术，1994（2）: 11-18.

[4]翁建华，潘增富，闵桂荣.任意形状凹面和相互可视表面φ2、φ3的分析计算[J].中国空间科学技术，1994（3）:9-16.

[5]徐向华，程雪涛，梁新刚.圆形太阳同步轨道卫星的空间热环境分析 [J].宇航学报，2012，33（3）: 399-404.

[6]胡日查，郭亮，刘春龙.非典型圆形轨道空间光学遥感器外热流计算[J].计算机仿真，2015，32（7）: 60-64.

[7]王宇宁.上面级轨道外热流算法研究[D].哈尔滨：哈尔滨工业大学，2010.

[8]张涛，孙冰.基于STL文件和有限元法的在轨航天器关键部件热计算[J].航空动力学报，2010，25（5）：999-1004.

[9]刘欣，潘增富.卫星在轨太阳辐射热流的简化计算方法[J].中国空间科学技术，2012，32（4）:15-21.

[10]关奉伟，刘巨，于善猛，等.空间光学遥感器热试验外热流模拟及程控实现[J].中国光学，2014，7（6）: 982-988.

[11]刘巨.太阳同步圆轨道空间相机瞬态外热流计算[J].中国光学，2012，5（2）:148-153.

[12]王宇宁，魏承，赵阳.考虑轨道摄动的外热流计算分析[J].上海航天，2012，29（5）:48-53.

[13]卢威，黄家荣，钟奇.载人运输飞船多模式和姿态的外热流[J].中国空间科学技术，2011，31（1）:25.

[14]孙创，夏新林，戴贵龙.飞行器复杂外结构的环境热流计算方法[J].宇航学报，2011，32（3）:683-687.

[15]潘晴.基于反向蒙特卡罗法的飞行器空间外热流计算[D].上海：上海交通大学，2012.

Study of external heat flux calculation method for interplanetary spacecraft in solar system

LIU Yang1，2，PENG Xiao-dong1，ZHANG Han-xun1，GUO Song1，2，MING Xing3
（1.National Space Science Center，Chinese Academy of Sciences，Beijing 100190，China；2.University of Chinese Academy of Sciences，Beijing 100049，China；3.Academy of Opto-electronics，Chinese Academy of Sciences，Beijing 100094，China）

Focus on the problem that the domestic traditional external heat flux calculation algorithm and some foreign commercial software only support single planet satellites'external heat flux calculation，this paper comes up with a solution which combining with the method of integration，the method of parallel light，the approximation method and the interpolation method.In the solution，the influence of planetary elliptical orbit and the occlusion of spacecraft's faces are considered.Simulation results show that the solution is in accordance with external thermal properties of the interplanetary orbit，meanwhile its computational efficiency and precision is high.

external heat flux；view factor；interplanetary orbit；spacecraft；radiation heat transfer

TN92

A

1674-6236（2017）09-0001-05

2016-07-07稿件编号：201607066

中国科学院科研装备研制项目（YZ201309）

刘 洋（1991—），女，山西阳泉人，博士。研究方向：航天系统建模仿真与可视化。