三联体类半带滤波器组的设计方法

地里木拉提·玉买江，吐尔洪江·阿布都克力木，黄允浒，古丽米热·米吉提

（新疆师范大学 数学科学学院，新疆 乌鲁木齐 830054）

三联体类半带滤波器组的设计方法

地里木拉提·玉买江，吐尔洪江·阿布都克力木，黄允浒，古丽米热·米吉提

（新疆师范大学 数学科学学院，新疆 乌鲁木齐 830054）

文中提出了一种由3个内核所定义的三联体类半带滤波器组的设计方法。采用了Lagrange半带滤波器组和Remez算法，具体地给出了分解滤波器的设计和重构滤波器的设计。带参数的Bernstein多项式用于构造内核。该滤波器组结构有完全重构，正则性等优点。确定Bernstein多项式的自由参数是利用最小二乘法得到。采用了两个实例，对实例进行了具体对比和分析。得出了这种设计方法很灵活，比较容易设计出不同性能的滤波器组。

FIR数字滤波器；半带滤波器组；三联体类；小波变换

离散小波变换在需要分解信号方面广泛应用，例如压缩，去噪，印刷等。在提供时-频分析方面，离散小波变换克服了传统傅里叶变换中的一些限制，而时-频分析是处理非稳定性信号所需要的[1-2]。设计小波滤波器相当于设计多重速率的完全重构滤波器组。传统滤波器和小波滤波器的主要区别在于在后一种情况下的正则性。正则性是混叠频率上实施零后所得到[3]。

结构上完全重构和正则性问题限制了滤波器系数，复杂了设计过程。设计过程相当于优化滤波器系数，它易受结构上完全重构和正则性的限制。这些限制如果直接用于实际问题上，将复杂设计过程并复杂优化。利用滤波器组结构替换直接法将会满足限制条件[4-5]。

文中提出一种结构上完全重构并利用三个半带的滤波器组。这有设计简单、充实造型，并且克服半带滤波器组的限制，这种滤波器组称为三联体半带滤波器组。下面的两个方法将用于设计三联体的半带滤波器组。第一个方法是利用Lagrange半带滤波器组，过滤器被最大化，转出低的流利度。第二个方法利用Remez算法[6]，结果会出现清晰的但没有正则性的等波滤波器。上述两种方法是滤波器组的两极端的特点。在本论文中，设计三联体半带滤波器组对上面所述的两种情况的巨大差距起一个桥梁作用。滤波器的正则性是利用带参数的Bernstein多项式提高清晰度来替换的。这个技术根据最小二乘法来实现的。迭代过程是用于解决最小二乘法问题。

1 三联体半带滤波器组和Bernstein多项式

本节所提的滤波器组是三联体类滤波器组。低通滤波器由以下等式得到

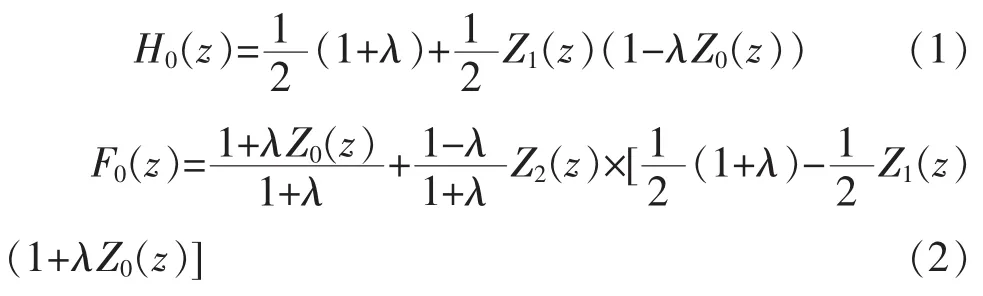
其中z0，z1，z2是从半带滤波器中获得，也就是1/2（1+Z0（z），1/2（1+Z1（z））和 1/2（1+Z2（z））是半带滤波器组。值得注意，式（1）和（2）提供了滤波器的零相位。

高通滤波器由以下式子得到

其中参数λ的范围在0≤λ≤1，当λ=0时，三联体类滤波器组会限制半带对滤波器组，半带对滤波器组有些限制其作为分析低通滤波器的频率响应将限制半带过滤器。分解和重构低通滤波器的频率响应的幅度在处ω=π/2，半带对滤波器组限制在0.5和1之间。然而对于三联体类滤波器组，当频率响应的幅度在ω=π/2可以选择任何一个适当的λ值。特别地当两个分解和重构低通滤波器组的频率响应的幅度在ω=π/2处是

值得注意，适当的重命名参数，上面的滤波器相当于文献[7]中的正交镜像滤波器。在文献[7]中所用的滤波器是与文献[4]中所用的滤波器是不同的。正交镜像滤波器大量用于Mallat算法[8]。

在本文中，设计内核利用带参数的Bernstein多项式[9]，即

其中当N是奇数时，α=[α0，α1…，α（N-1）/2]T，并且

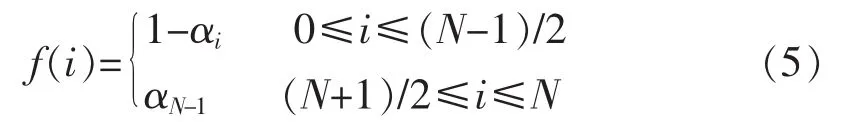
通过半带滤波器的Z变换，传递函数得到的x≡-（1/4）z（1-z-1）2将代入到式（4）中，内核由以下等式给出

值得注意改变多种Bernstein多项式，自然地给滤波函数零相位和三联体类滤波器组的零相位。式（1）和式（2）都在这里使用。结果滤波器H0和F0的长度分别是

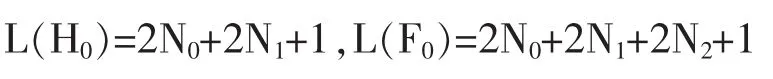
2 自适应参数最小二乘法的设计

BN0代入式（6）中，BN1

代入式（7）中，BN2代入式（8）中分别用B0（x），B1（x）和B2（x）表示，那么B0（x），B1（x）和B2（x）分别等于

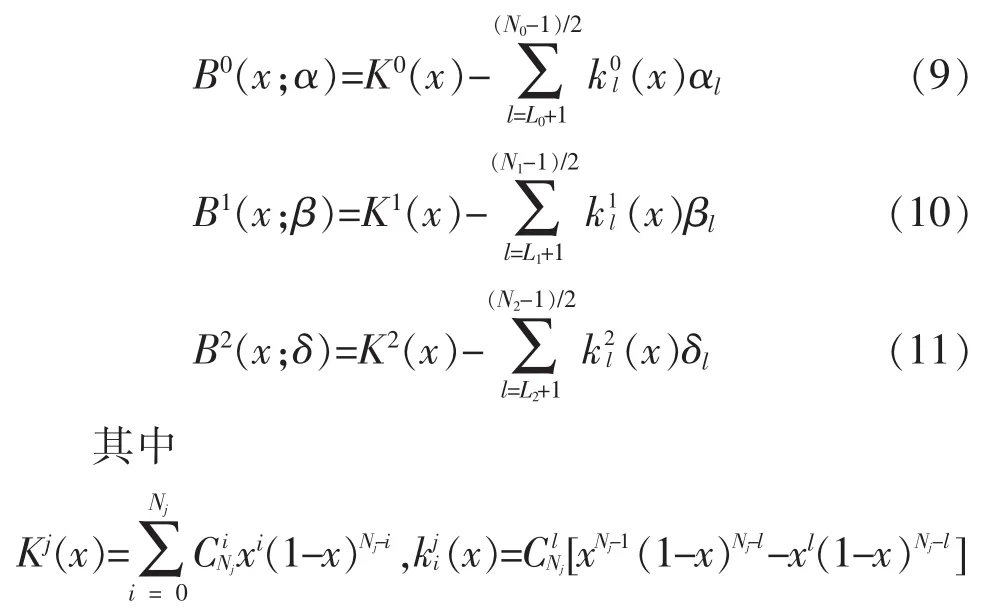
2.1 分解滤波器H0的设计

利用以上等式，可以看出滤波器（1）可以表示为如下两个形式：

从这可以看出H0是带参数的多重线性函数。特别是H0对α线性的（当β固定时）和对β线性的（当α固定时）。值得注意的是α，β可以同时不同，但H0是对自由参数α和β时不会是线性的。

2.2 重构滤波器F0的设计

利用式（9）-（11）可以看出（12）式中的滤波器为

其中

从式（14）中可以看出F0对参数啄是线性，参数α，β从分解滤波器的设计中得到。

3 设计实例

例1：N0=N1=7，N2=5。滤波器H0和F0的长度各自分别为29和39。选择L0=L1=L2=2，（α0=α1=α2=β0=β1=β2=啄0=啄1=啄2=0）且两个滤波器都六级正则性，也就是每个滤波器在 z=-1处六重零优化 cp=0.4（ωp=0.436π），cs=0.8（ωs=0.705π），γ=0.5。优化的自由参数值为α3=-0.044 06，β3=-0.494 8，因此，α=（α0α1α2α3）=（0 0 0-0.044 06），β=（β0β1β2β3）=（0 0 0-0.49 48）。

在图1中给出了滤波器组的频率响应图和所有参数为0时最大的响应图和利用雷米交换算法设计一对等波纹。等波纹的阻带波纹的大小是和最小二乘法优化滤波器的波纹大小是相同。通过对波纹的最大化，我们很容易看到对例题所对应图的清晰度增加了。等波纹明显的出来，但z=-1处没有零，也就是在ω=π附近低消弱。

例2：N0=N1=7，N2=5。滤波器H0和F0的长度各自分别为29和39。选择L0=L1=L2=1（α0=α1=β0=β1=0）和L2=2（γ0=γ1=γ2=0）并且两个滤波器都四级正则性也就是每个滤波器在z=-1处四重零优化cp=0.4，cs=0.8，γ=0.5。

优化的自由参数值为α=（α0α1α2α3）=（0 0-0.6203 -0.2523），

滤波器组的频率响应图在图2中给出，同时表明通过阻止正则性提高锐度。

图3画出了尺度函数和小波函数的图像。

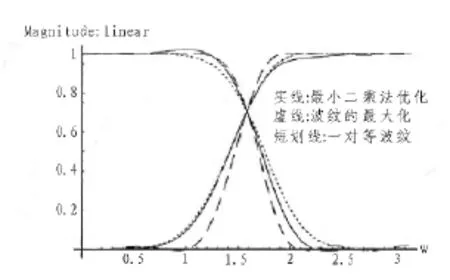
图1 例1中H0，H1的频率响应图

图2 例2中H0，H1的频率响应图

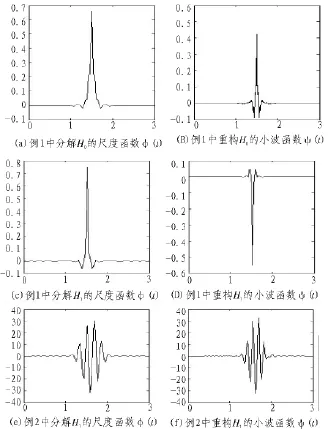
图3 尺度函数（t）和小波函数ψ（t）

4 结 论

文中给出了双正交滤波器组的设计方法。我们使用了三联体的半带滤波器组和Bernstein多项式，并且确认在结果上施加完全重构和约束条件。滤波器传送函数是一个带自有参数的多重线性函数并产

生重复二次目标函数。迭代过程是为了处理最小乘方问题。多种设计实例的给出为了显示设计技术的有效性和灵活性。滤波器的正则性容易替换增加频率响应的清晰度转出。光滑的对称拓展和小波函数容易得到。值得注意，不可分的二维滤波器组可以转换成一维的滤波器组。

[1]INGLE V K，PROAKIS J G.数字信号处理（MATLAB版）[M].柳树棠，陈志刚，译.西安：西安交通大学出版社，2013.

[2]ABDUKIRIM T ，ROZIA.Design of Dyadic Wavelet Filters With Vanishing Moments Using Dyadic Lifting Scheme.IEEE International Conference on Intelligent Computing and Intelligent systems，2011（3）:150-222

[3]吐尔洪江·阿布都克力木.小波信号处理基础[M].北京：北京邮电大学出版社，2014.

[4]杨松涛.完全重构滤波器组优化及其在宽带信道化中的应用[D].西安：西安电子科技大学，2014.

[5]Tay D B H.Two-stage，least squares design of biorthogonal filter banks using transformations of variable[J].IEEE Trans.Circuits Systems，2000（1）：591-594.

[6]Phoong S M，Kim C W，Vaidyanathan P P，et al.A new class of two-channel biorthogonal filter banks and wavelet bases[J].IEEE Trans.Signal Processing，1995（43）：649.

[7]任堰牛，青小渠.FIR半带滤波器的简化结构及其仿真研究[J].兵工自动化，2013（3）:53-56.

[8]段佳佳，樊龙龙，张波涛.基于MATLAB的FIR滤波器的设计[J].电子测试，2011（8）:19-21.

[9]K.Maleknejad，E.Hashemizadeh，B.Basirat.Computational method based on Bernstein operational matrices for nonlinear Volterra-Fredholm-Hammerstein integral equations [J].Communications in Nonlinear Science and NumericalSimulation，2011（1）：100-150.

[10]韦柳泰.一种双通带微带滤波器的设计[J].电子科技，2012（6）:98-103.

[11]H.Caglar，A.N.AKansu.A generalized parametric PR-QMF design technique based on Bernstein polynomial approximation，IEEE trans.Signal Processing，1993（41）：2314.

[12]周明，童创明，付树洪，等.一种新颖的小型宽阻带低通滤波器[J].电讯技术，2010（4）:74-77.

[13]Tay D B H.Design of filter-banks/wavelets using TROV:A survey.Digital Signal Processing，1997，4（7）：229-238.

A novel approach to design the class of triplet halfband filterbanks

Dilmurat·OMAR，Turghunjan·ABDUKIRIM，HUANG Yun-hu，Gulmira·MIJIT
（School of Mathematical Sciences，Xinjiang Normal University，Urumqi 830054，China）

A new approach to is presented for designing the class of triplet halfband filter bank which are defined by three kernels.Adopted Lagrange half band filters and Remez algorithm which are specific given analysis filterbank and decomposition filterbank.The parametric Bernstein polynomial is used to construct the kernels.The design of the free parameters of the Bernstein polynomial is achieved through a least squares method.The filterbank have the advantage of structural perfect reconstruction and structural regularity.Using two examples to concretely comparison and analysis.The design technique is flexible in that allows filter with different characteristic to be design with ease.

FIR digital filters；halfband filters；triplet；wavelet transform

TN713.4

A

1674-6236（2017）09-0010-04

2016-07-05稿件编号：201607034

国家自然科学基金资助项目（11261061；61362039；10661010）；新疆维吾尔自治区自然科学基金资助项目（200721104）

地里木拉提·玉买江（1993—），男，新疆喀什人，硕士研究生。研究方向：小波分析及其应用。