基于QRD-LS算法的新型预失真方法

纪广玉，黄永辉

（1.中国科学院大学 北京100190；2.中国科学院国家空间科学中心 北京 100190）

基于QRD-LS算法的新型预失真方法

纪广玉1，2，黄永辉2

（1.中国科学院大学 北京100190；2.中国科学院国家空间科学中心 北京 100190）

针对卫星通信系统记忆功率放大器引起的非线性失真，提出了一种单路计算方法与QRD-LS算法相结合的新型预失真方法。该方法基于记忆多项式模型与间接学习结构，采用基带I、Q信号中的一路作为最小二乘算法的输出，同时预失真训练器输入矩阵由复数转化为实数；基于Givens变换的QR分解避免了最小二乘算法直接对矩阵求逆。针对16QAM调制信号与AB类功放模型进行仿真，结果表明：系统EVM从6.2%提升到0.8%，带外功率谱抑制20 dB。

卫星通信；单路计算；QRD-LS；数字预失真

为了提高卫星通信的性能，高阶调制方式得到了越来越广泛的应用。工程中为了提高卫星通信系统的功率效率，功放需要被推到饱和点工作[1]。高阶变包络调制信号经过饱和功放后会导致系统产生失真，表现为带内失真，信号幅度和相位的失真，造成系统接收端误码率提高等；带外失真，信号邻信道功率比提高，频谱利用率降低。为了补偿功放产生的失真，线性化技术得到了广大学者的研究。前馈[2]、反馈[3]、模拟预失真[4]等方法属于模拟校正，对发射机电路复杂性、稳定性造成影响。数字预失真因性能稳定、高效、宽带、自适应等优点是补偿功放非线性失真与记忆效应有效的方法[5]。

最小二乘算法（least square，LS）[6]被广泛应用于记忆多项式预失真参数的计算。在LS算法求解时会出现矩阵求逆，当矩阵维度非常大的时候对其求逆复杂度很高。基于QR分解的LS算法（QRD-LS）[7]解决了LS算法中矩阵求逆的难题。由于高阶调制信号由同相分量与正交分量组成，此时LS算法的输入矩阵为复数矩阵。文中提出了一种基于单路信号的改进QRD-LS算法，将输入矩阵由复数转化为实数进行处理。

1 基于单路计算方法的数字预失真方法

数字预失真的原理是通过预失真算法得到功放逆模型，将其逆模型赋予预失真器，使预失真器与功放的串联系统为线性系统。数字预失真结构分为：直接学习结构[8]与间接学习结构[9]。直接学习结构采用一定的算法得到功放模型，再对模型进行求逆得到预失真器的模型参数。间接学习结构（图1）不需要先辨识出功放的模型就可以直接得到预失真器的模型参数，易于工程实现[10]。在高阶调制信号中，输入信号由I、Q两路信号组成，为了得到预失真器的模型参数，需要对I、Q两路信号同时进行运算[11]。

图1 间接结构

1.1 单路信号计算方法

Volterra级数模型能够很好的描述功放的非线性记忆效应，由于参数较多不利于求解，在工程应用中受到限制[12]。一些学者提出了简化的Volterra级数模型即记忆多项式模型[13]。文中采用记忆多项式模型作为预失真器的模型，其输入输出关系如下式：

K为非线性阶数，M为记忆深度，ckm为记忆多项式的复系数。设复系数ckm=akm+j*bkm，复信号y=yI+ j*yQ。代入式（1）可以表示为:

从式（3）、（4）可以看出，只需功放反馈采样信号y与功放输入信号中的一路（zI或zQ）就可以得到预失真器的参数。因此本文预失真结构如图2所示。

图2 本文方案框图

1.2 基于Givens变化的QRD-LS算法

基于 Givens变换的QR分解可以用来解决LS算法中直接对矩阵求逆的难题，并且可以在FPGA上实现。

文中预失真器采用记忆多项式模型。采用本文提出的单路计算方法，此时预失真训练器输入输出关系可表示为：zI=Yc，其中zI是预失真训练器的输出I路信号，Y是预失真训练器的输入矩阵，c为需要求得的预失真器参数。用矩阵形式可以表示为：

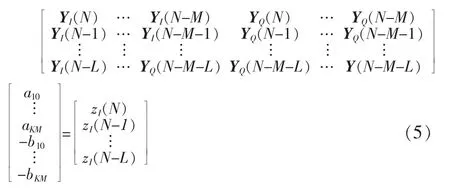
其中Y（N-m）=[y（N-m），y（N-m）|y（N-m）|2，…，y（N-m）|y（N-m）|K-1]，k为奇数；此时输入矩阵为实数矩阵。

采用最小二乘求解，预失真器参数可表示为：

对Y矩阵进行QR分解，则Y=QR（Q是正交矩阵，R为上三角矩阵），带入式（6）可得:

由于R是上三角矩阵，因此式(7)可以表示为:

由上式可得预失真器参数：

2 仿真结果与分析

为了验证本文所提出方案的合理性，在MATLAB上进行仿真验证。功放模型采用AB类记忆深度为2，非线性阶数为5的奇次记忆多项式模型[14]，参数如下所示：

2.1 AM/AM、AM/PM曲线

在加入预失真前后，功放的动态AM/AM,AM/ PM曲线如图3所示，从图中可以清楚的看出在加入预失真之后，功放的AM/AM特性曲线为一条直线。AM/PM曲线也得到了改善。

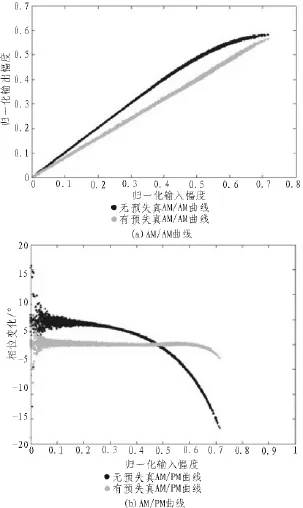
图3 功放动态曲线

2.2 星座图分析

由于功放非线性特性影响，16QAM信号[15]经过功放后不仅表现为幅度失真，而且信号的相位也会发生变化。图4为预失真器加入功放前后输出信号星座图的对比，从图中可以看出信号经过预失真器之后，星座图得到了很好的矫正。

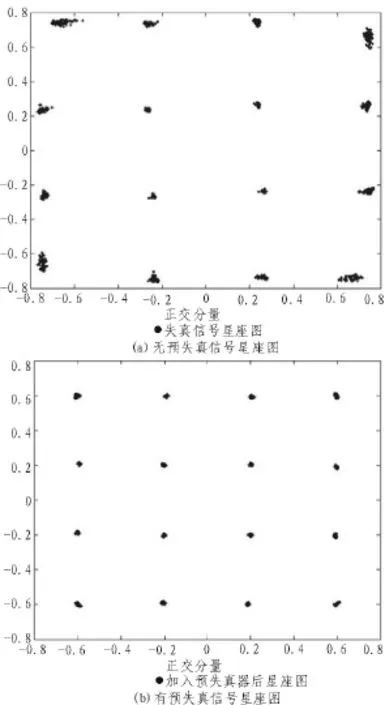
图4 加入预失真前后星座图比较

EVM是衡量衡量通信系统的重要指标，仿真得到了本文提出的方法使系统EVM从6.2%提升到0.85%。

2.3 信号功率谱分析

由于信号直接经过功放之后会产生带外失真，信号功率谱会泄露到相邻信道。下面从信号功率谱角度，分析本文设计的预失真方法的性能。

图5 信号功率谱密度

从图5中可以看出在无预失真条件下，信号经过功放之后频谱向邻信道扩散，信号邻信道功率比提高。在加入本文提出的预失真方法之后，邻信道互调功率降低约20 dB。

3 结 论

为了补偿功放的非线性失真，本文提出了一种基于记忆多项式模型的单路计算预失真器设计方法。该方法将传统QRD-LS算法的输入矩阵由复数转化为实数来计算。最后通过星座图、信号功率谱、AM/AM、AM/PM曲线分析了所提出方案的性能。

[1]韩冰，晋东立.卫星通信中16QAM信号的数字预失真研究[J].飞行器测控学报，2015（2）:184-188.

[2]Young Yun Woo，Youngoo Yang，Jaehyok Yi，et al. Feedforward amplifier for WCDMA base stations with a new adaptive control method[C]//Microwave Symposium Digest，2002 IEEE MTT-S International，2002，2（7）:769-772.

[3]Kim Y，Yang Y，Kang S，et al.Lineariza-tion of 1.85-GHz amplifier using feedback predistortionloop[C]//Microwave Symposium Digest,1998 IEEE MTT-S International，1998（3）:1675-1678.

[4]Morris K A，McGeehan J P.Gain and Phase Matching Requirements of Cubic Predistortion Systems[J].Electronics Letters，2000，36（21）:1822-1824.

[5]Rawat M，Rawat K，Ghannouchi F M.Adaptive digital predistortion of wireless power amplifiers/ transmitters using dynamic realvalued focused timedelay line neuralnetworks[J].IEEE Transactions on Microwave Theory and Techniques, 2010，58（1）:95-104.

[6]Ding L，Ma Z，Morgan D R，et al.A least-Squares/ Newton method for digital predistortion of wideband signals[J].IEEE Transactions on Communications.，2006，54（5）:833-840.

[7]Dian X，Zhibin Z.An improved adaptive LS algorithm using QR decomposition fordigital predistortion[C]//Automatic Control and Artificial Intelligence（ACAI 2012），International Conference on，2012:416-419.

[8]Choi S，Jeong E R，Lee Y H.A Direct Learning Structure for Adaptive Polynomial-Based Predistortion for Power Amplifier Linearization[C]// VehicularTechnologyConference，2007.VTC2007-Spring.IEEE 65th，2007:1791-1795.

[9]Montoro G，Gilabert P L，Bertran E，et al."A new digital predictive predistorter for behavioral power amplifier linearization，" IEEE Microwave and Wireless Components Letters，2007，17（6）:448-450.

[10]刘高辉，杨韶，杨媛，等.幅度和相位预失真参数并行估计的间接学习结构预失真方法[J].信号处理，2013（4）:520-526.

[11]詹鹏,秦开宇,蔡顺燕,单路反馈射频功放预失真线性化方法[J].电子与信息学报，2011（8）:2023-2027.

[12]吕海飞，夏红娟，韩非.基于简化VOLTERRA级数的数字预失真系统设计方法[J].制导与引信，2011（4）:42-45.

[13]Dennis R Morgan，Zhengxiang Ma，Jaehyeong Kim，et al.A Generalized Memory Polynomial Model for Digital Predistortion of RF Power Amplifiers[J]. IEEE Transactionson signalprocessing，2006，54（10）:3852-3860.

[14]Ding L，Zhou G T，Morgan D R，et al.A robust digital baseband predistorter constru cted using memory polynomials[J].IEEE Transactions on Communications，2004，52（1）:159-165.

[15]陈彦丽，郭明安，罗通顶，等.快前沿程控高压脉冲信号发生器研制[J].现代应用物理，2016（4）：73-76.

New predistortion method based on QRD-LS algorithm

JI Guang-yu1，2，HUANG Yong-hui2
（1.University of Chinese Academy of Sciences，Beijing 100190，China；2.National Space Science Center，Beijing 100190，China）

For satellite communications systems，this paper presents a new method for predistortionthat combine single path calculation algorithm and QRD-LS.The method is based memory polynomial model and indirect learning structure，using one route of the input signals（I or Q）astheoutput of least squares algorithm，while predistortion trainer input matrix by a complex into a real number；Based on Givens QR decomposition to avoid the least-squares algorithm for matrix inversion directly.Simulation based on the 16QAM modulation signal and Class AB modelshows that system EVM decreased from 6.2%to 0.8% and 20dB out-bandsuppression.

satellite communication；single path calculation；QRD-LS；digital predistortion

TN919

A

1674-6236（2017）09-0171-04

2016-03-30稿件编号：201603406

纪广玉（1992—），男，河南新乡人，硕士研究生。研究方向：电子与通信工程。