一种基于雷达微多普勒效应苍蝇识别的方法

沈菲菲，李立钢，贾配洋，宋振健

（1.中国科学院国家空间科学中心，中国科学院复杂航天系统电子信息技术重点实验室，北京100190；2.中国科学院大学 北京100049）

一种基于雷达微多普勒效应苍蝇识别的方法

沈菲菲1，2，李立钢1，贾配洋1，2，宋振健1，2

（1.中国科学院国家空间科学中心，中国科学院复杂航天系统电子信息技术重点实验室，北京100190；2.中国科学院大学 北京100049）

为了有效地识别苍蝇，提出了利用雷达的微多普勒效应来识别的有效方法。首先，根据微多普勒效应的基本概念，建立了苍蝇飞行复合运动的雷达回波模型，推导了雷达回波信号和理论的多普勒频率，提出了综合运用时频分析（伪Winger-Ville变换）、谱图峰值估计、参数拟合、平动补偿的方法，最终提取出苍蝇在飞行过程中的运动参数，包括：振翅频率、振动幅度、运动速度、加速度。

微多普勒；复合运动；伪Winger-Ville变换；参数拟合；谱图峰值估计；平动补偿

随着社会的发展，生活水平的提高，人们对食品安全越来越关注。而由媒介生物传播的疾病史整个食品加工过程中非常值得关注的一个问题，在许多食品加工场所中，苍蝇是最常见的一种害虫，在食品的表面和加工操作表面停留，通过其直接接触、呕吐物以及排泄物传播多种致病菌和寄生虫，导致疾病的发生。所以食品加工和食品服务场所必须适时采取必要的放置措施[1]。

目前，防治虫蝇的有效手段主要有以下几种：物理防治技术：应用各种物理因子如光谱、点、颜色、温度、湿度、声音等机械设备来防治[2]以及无公害粘虫胶等物理手段。但是这些方法均不太适合于场所大的食品加工厂等场所。

雷达成像中，一般将目标或者目标部件除质心平动之外的振动、旋转和加速运动等微小运动统称为微动[3]，而由目标微动产生的对雷达回波信号的展宽频率调制称为微多普勒效应（micro-Doppler effect）[4]。这种微动对雷达回波的调制称为微多普勒现象[5-6]。微多普勒现象可以反映目标的精细运动特征[3-7]，它在目标的探测、分类、识别领域都具有很大的应用潜力[8]。近年来，许多有效的微多普勒信号提取技术相继被提出，例如时频分析技术[9-13]、逆Radon变换[14]方法等。

文中提出了一种基于雷达微多普勒效应识别目标苍蝇的方法。不仅无色无味没有公害，而且成本低易于实现。

1 雷达识别苍蝇的微动模型及数学原理

以雷达Q建立参考坐标系Q（U，V，W），由于苍蝇相对于雷达距离来说很小，可以假设为点目标，其振翅中心记作O，以O为原点建立一个与Q（U，V，W）平行的坐标系（X，Y，Z）。模型如图1所示。

图1 基于雷达的苍蝇微动物理模型

O在雷达坐标系中，其方位角和仰角分别为α和β，O与雷达的距离为R0。因此振动中心O点的坐标可以表示为：

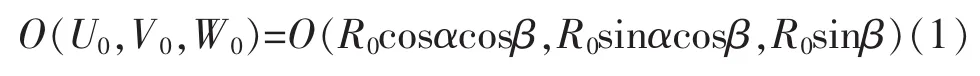
雷达发射方向的单位向量为：

假设在雷达坐标系中，目标的振动方向为：方位角αp，仰角βp，最大振幅Dv，振动频率fv，因此目标的振动形式可以表示为：

振动方向的单位矢量是：

任意时刻，目标与雷达的距离为：

所以t时刻，目标与雷达的距离：

通常情况下Rt＞＞Dt，则（6）式可以近似为

雷达回波：

其中，ρ是点目标的反射率，f0是发射信号的载频，表示相位调制函数。对Sr（t）利用K阶Bessel函数，

展开可得微多普勒频谱是以中心频率f为中心的对称分布，相邻谱线的间隔为

t=0时刻，点目标P在（X0，Y0，Z0），t0时刻移动到：

对应的速度为：

根据式，对应的微多普勒频率为：

从式（12）可看出第一项为平动引起的多普勒频率，第二项和第三项分别是由于加速运动和苍蝇翅膀振动引起的微多普勒频率。如果补偿掉平动和加速运动，则翅膀振动引起的微多普勒频率是：

式（12）表明：由平动引起的多普勒频率是一个常量，由于加速运动引起的微多普勒频率是随时间成正比变化。而由于振动引起的微多普勒频率是随时间成周期性变化的，变化周期与振动周期相同，变化幅度与振动幅度和振动频率成正比。由此可见先补偿掉平动和加速运动带来的多普勒频率，然后就可以通过振动引起的微多普勒来提取各个微动的各个参数。

2 雷达微动特征提取技术

雷达目标微动特征提取主要是从雷达回波信号中获取反映目标运动、结构等信息的特征量，基于特征量实现对目标微动参数估计，为目标的识别提供基础。

2.1 基于伪Winger-Ville变换的曲线参数提取

从公式（9）得到的雷达回波信号的形式可以看出，信号频率是随着时间而不断变化的，即微多普勒信号是一个非平稳时间信号。因此传统的傅里叶变换方法（Fourier Transform）求出的频率将不再能反应信号频率随时间变换的情况。因此有效的提取微多普勒需要使用高分辨的联合时间-频率分析方法。时频分析方法是提取目标微动特征的有效方法之一，也是应用最广泛的一类方法，它能够观察到信号的频率随时间变换的规律。常见的时频分析方法主要有两种：一种是线性变换，短时傅里叶变换（STFT），小波变换 （Gabor）；另一种是双线性变换，Winger-Ville分布，伪 Winger-Ville分布（PWVD），平滑伪Winger-Ville分布（SPWV）[5]。

Winger-Ville分布是时频分析方法中最早问世的，它是一种基于自相关系数的非线性时频分布，但WVD受交叉项干扰严重影响，故本文引入时域加窗的伪魏格纳分布（Pseduo，PWVD，PWVD），其表达式如下：

对其进行离散化处理，其离散化的表达式为：

典型的伪Winger-Ville变换分布如图3所示。本论文，从实际雷达布局出发，对公式（9）中的回波信号进行伪Winger-Ville变换，和图2中的理想多普勒频率图对比可知，伪Winger-Ville变换可以得到振动目标微多普勒效应的轮廓。

图2 伪winger-ville变换分布图

2.2 谱图峰值估计分析

从图2知，我们不能够精确的得到每一时刻对应的微多普勒频率，即瞬时频率无法得到。同样振动幅度也无法精确得知。而谱图峰值估计算法估计的瞬时频率是其峰值在时频平面上的投影，是对目标瞬时频率的提取，进一步表征信号的特征参数，从而达到对目标的识别。假设信号的时频变换频谱为：W（m，k），其中1≤m≤M，1≤k≤N，谱图峰值估计算法原理为：

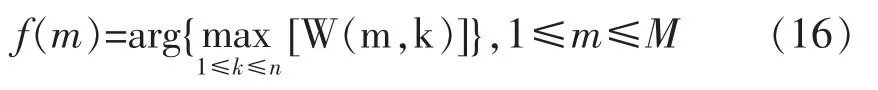
式中，arg{·}为计算在任意时间t，幅度达到最大值对应的频率值。

本论文对得到的伪Winger-Ville变换图采用谱图峰值估计法来提取目标的瞬时频率，从而确定信号谱图峰值的具体位置。因此可以得到瞬时频率，以及每一时刻对应的信号幅度。

2.3 曲线拟合工具Curve Fitting Tool

Matlab有一个功能强大的曲线拟合工具箱cftool，能够实现多种类型的线性、非线性曲线拟合。我们要得到微动特征的各个参数，可以使用cftool方法进行数据拟合。cftool曲线拟合窗口如图3所示。

图3 Curve Fitting Tool窗口

式（12）表明，可以先用cftool中的直线拟合法f（x）=p1*x+p2来得到苍蝇飞行的平动速度和加速度。综合p1，p2和式（12），可估计出：

从而补偿掉平动带来的多普勒频率和加速运动带来的微多普勒频率。之后再利用cftool中的正弦拟合法 f（x）=a1*sin（b1*x+c1），对应的求解到振翅频率fv和振动幅度Dv

综上分析，综合利用时频分析法、参数拟合法结合拟合工具来快速提取识别苍蝇的具体步骤如下：

步骤1构建基于雷达的苍蝇微动物理模型，理论上求得微动带来的雷达回波信号和微多普勒频率值，为下一步信号处理以及验证理论正确性提供数据支持；

步骤2对雷达回波信号进行时频分析，得到目标微多普勒信号的伪Winger-Ville时频分布骨架S（t，f）；

步骤3对S（t，f）采用谱图峰值估计法，求得微多普勒效应的瞬时频率；

步骤4对经过谱图峰值估计法得到的瞬时频率进行matlab线性参数拟合，利用式（16）求得苍蝇运动的速度和加速度；

步骤5利用得到的速度v0，加速度a补偿掉线性的多普勒频率，在利用matlab正弦参数拟合得到振翅频率fv和振动幅度Dv；

3 仿真实验

3.1 微动参数估计

设雷达工作在X波段，载频发射信号载频f0=10 GHz。苍蝇的振翅频率约三百五十二次，飞行速度是6～8 km/h，所以为了验证理论的正确性，本文假设振动频率fv=350 Hz，振动幅度Dv=0.06 m，平动速度v0=2 m/s，加速度a=10 m/s2，苍蝇沿着雷达视线方向（LOS）飞行和加速。对雷达接收到的回波信号进行伪Winger-Ville变换。信号采样率是fs=50 000 Hz，画图时候的时间间隔选取0.05 s。PWVD仿真结果如下图4所示，其中选择的窗函数宽度为47。从图中大致可以看出频率随时间变换的轮廓，但不能得到精确值。所以，仍需进一步处理。

对经过伪Winger-Ville的信号进行谱图峰值估计，谱图峰值检测之后得到单值的时频曲线，峰值检测后的瞬时频率与式（12）对应求得的理论多普勒频率如图5所示。

图4 回波信号伪winger-ville变换图

图5 理想多普勒频率和检测出的瞬时频率对比图

由图5可知，经过谱图峰值估计检测到的瞬时频率和理想的微多普勒频率在幅度和频率上相差很小，可以初步确定方法的正确性。但精确的数值从波形上无法用肉眼得到。对经过峰值检测后瞬时频率波形进行采样，采样率仍然是fs1=50 000 Hz，为了能用肉眼看得更清晰一些，本文时间只选取前0.02s时间内可得到10 000组数据，对采样后得到的10 000组数据进行matlab曲线线性拟合f（x）=p1*x+p2。

拟合出的斜率和截距值分别是 p1=637.8；p2=137.1，所以根据式（16）可求得

补偿掉平动和加速运动后，目标振翅带来的微多普勒频率为：

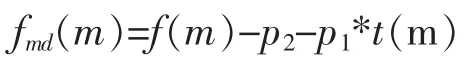
其中，f（m）是经过谱图峰值估计检测后的频率随时间变换的数据组。

经过上式修正后的苍蝇振翅带来的微多普勒频率如图6所示。

平动补偿后再利用matlab正弦拟合f（x）=a*sin（b*x+c），拟合出的数据值为：a=5648，b=2199，c=1.571

由参数b和式（14）可以得到

将振动频率代入上式即可得到：

振动频率Dv=0.066 516 m

图6 平动补偿后的时频曲线

3.2 性能分析

微振动参数的求解质和实际真实的理论值对比如表1，可知误差控制在0.0052%-10%之间，其中振动频率误差只有0.0193 Hz，由此可见能够利用微多普勒效应来准确的识别到振翅的苍蝇，这对于食品行业生产加工储藏过程中捕捉苍蝇价值重大。同时，能够检测到苍蝇飞行的速度、加速度，为进一步捕捉飞行中的苍蝇提供数据支持。从表格可以看出，振动幅度DV误差较大，原因可能是:1）振动幅度是通过先计算出振动频率 fv，代入（19）中的fv本身就有一定的误差，可能因此引入二次误差；2）在推导数学原理公式过程中做了一些近似。

4 结束语

微动目标的雷达回波相位中包含着目标微动的运动信息，而特征提取和微多普勒现象是一个新的研究方向。目前，国内外对于复合微运动带来的微多普勒效应研究较少，尤其是对于像苍蝇振翅频率约300多Hz频率的微运动研究更少。本文提出了一种利用微多普勒效应来识别苍蝇的新方法，并为捕捉苍蝇提供了数据支持。在提取微动参数过程中，综合利用了时频分析、谱图峰值估计、平动补偿、参数拟合的方法得到了微动所有参数确切的值，即振动频率、震动幅度、平动速度、加速度，误差控制在0.0052%～10%之间。

表1 微振动参数理论值和测量值

[1]JamesAustin，DawnCalibeo-Hayes.有效防治害虫，捍卫食品安全[J].食品安全导刊，2009（5）:71-72.

[2]周建波.无公害粘虫胶在害虫综合治理中的应用技术研究[D].保定：河北农业大学，2008.

[3]Chen VC，LI F，HO S S，et al.Micro-Doppler effect in radar:Phenomenon，model and simulation study [J].IEEE Transactions on Aerospace and Electronic Systems，2006，42（1）:2.

[4]Chen VC.Micro-Doppler effect of micro-motion dynamics:a review[C]//Processing of SPIE on Independent Component Analysis，Wavelets，and Neural Networks[C].Orlando，USA:SPIE Press，2003.

[5]王宝帅，杜兰，刘宏伟，等.基于经验模态分解的空中飞机目标分类[J].电子与信息学报，2012（9）:2116-2121.

[6]关永胜，左群声，刘宏伟，等.空间进动目标微动参数估计方法[J].电子与信息学报，2011（10）:2427-2432.

[7]张群，罗迎，何劲.雷达目标微多普勒效应研究概述[J].空军工程大学学报：自然科学版，2011，12（2）:22-26.

[8]LuoYing，ZhangQun，Qiu Cheng-wei，etal.Micro-Doppler effect analysis and feature extraction in ISAR imaging with stepped-frequency chirp signal[J]. IEEE transactions on Geoscience and Remote Sensing，2010，48（4）:2087-2098.

[9]肖金国，杜兰，韩勋，等.基于参数化时频分析的进动锥裙目标瞬时微多普勒频率提取方法[J].电子与信息学报，2016（1）:90-96.

[10]罗迎，张群，朱仁飞，等.多载频MIMO雷达中目标旋转部件三维微动特征提取方法 [J].电子学报，2011（9）:1975-1981.

[11]何劲，张群，罗迎，等.逆合成孔径成像激光雷达微多普勒效应分析及特征提取 [J].电子学报，2011（9）:2052-2059.

[12]曹文杰，张磊，杜兰，等.基于瞬时频率估计的进动锥体目标微多普勒频率提取方法[J].电子与信息学报，2015（5）:1091-1096.

[13]Gao Hongwei，Xie Lianggui，Wen Shuliang，et al. Micro-Doppler signature extraction from ballistic target with micro-motions[J].IEEE Transactions on Aerospace and Electronic Systems，2010，46（4）: 1969-1982.

[14]梁必帅，张群，娄昊，等.基于微动特征关联的空间非对称自旋目标雷达三维成像方法[J].电子与信息学报，2014（6）:1381-1388.

A method of recognizing flies based on radar micro-doppler effect

SHEN Fei-fei1，2，LI Li-gang1，JIA Pei-yang1，2，SONG Zhen-jian1，2
（1.National Space Science Center/Chinese Academy of Sciences，Beijing 100190，China；2.University of Chinese Academy of Sciences，Beijing 100049，China）

In order to effectivelyidentify flies，this paper proposes an effective method of using radar micro-Doppler effect to recognize flies.Firstly，according to the basic concept of the micro-Doppler effect，the radar echo model of composite motion of a fly is established，then the radar echo signal and theory Doppler frequency is derived.A method of comprehensive application of the frequency analysis（pseudo Winger-Ville transform），the peak spectrum estimation，parameterfitting，motion compensation is proposed.Finally，the motion parameters of the fly during the flight are extracted. Including:flapping frequency vibration amplitude，velocity，and the acceleration.

MicroDoppler；compositemotion；pseudo Winger-Ville transform；parameter fitting；peak spectrum estimation；motioncompensation

TN95

A

1674-6236（2017）09-0022-05

2016-07-02稿件编号：201607009

中科院创新基金（CXJJ-15S146）

沈菲菲（1992—），女，河南濮阳人，硕士研究生。研究方向：计算机仿真以及信号处理。