基于Logistic回归模型的赤足迹的性别分析

姬瑞军，汤澄清，王明月

（中国刑事警察学院 辽宁沈阳 110035）

基于Logistic回归模型的赤足迹的性别分析

姬瑞军，汤澄清，王明月

（中国刑事警察学院 辽宁沈阳 110035）

目的：犯罪现场遗留足迹的性别。方法：选取足迹长、足迹掌宽和足迹跟宽特征作为自变量，性别作为因变量，建立左、右足logistic回归模型。样本：410名男女左、右赤足迹样本（其中男性207名，女性203名），测量了足迹长、足迹掌宽和足迹跟宽等特征。结论：所获取的模型对左足赤足迹的性别预测正确率为88.8%，对右足赤足迹的性别预测正确率为90.0%，均具有较高的性别预测准确率。在一定条件下，所建立的数学模型可以为现场勘验人员对赤足迹的性别分析提供参考。

赤足迹；性别；足迹长；足迹掌宽；足迹跟宽；logistic回归

近年来，随着社会的发展，犯罪现象呈现出新的规律和特点，犯罪主体的新特点主要表现在女性犯罪的增多。在我国“文化大革命”以前，女性犯罪占犯罪总数的5%左右，20世纪70－80年代，占整个犯罪的6－7%，现在则达10－20%，数量直逼德国［1］。众所周知，犯罪必然会留下痕迹，足迹又是犯罪现场的重要痕迹之一，随着女性犯罪的比例增多，对犯罪现场遗留足迹的性别研究是非常必要的。本文结合我国足迹勘验技术，选取赤足迹的足迹长、足迹掌宽和足迹跟宽作为变量，性别作为因变量，运用统计学的方法，建立logistic线性回归模型，用量的方法对赤足迹进行性别分析。

一、材料和方法

（一）材料。

随机选取身体健康，无残疾，无足病史的207名成年男性和203名成年女性，分别收集每人左、右足清晰的静态油墨捺印足迹样本各一枚。其中，男性年龄在25±5岁，女性年龄在25±5岁。对获取的赤足迹捺印样本使用传统的足迹测量方法[2]对足迹长、足迹掌宽、足迹跟宽进行测量。其中，足迹长是赤足迹沿足迹中心线方向上的最长距离；足迹掌宽是赤足迹掌内外侧突点间的距离；足迹跟宽是赤足迹跟内、外侧突点间的距离。为了便于实验数据的处理，规定左足迹长、左足迹掌宽、左足迹跟宽、右足迹长、右足迹掌宽、右足迹跟宽分别记为LFL、LFB、LFHB、RFL、RFB、RFHB。

（二）方法。

将所获取的数据输入到SPSS 20.0软件进行统计学分析。为了获取男性和女性足迹中差异较明显的变量，使用独立样本T检验比较变量在性别间是否存在显著性差异。使用配对样本T检验比较左、右足间的数据是否存在显著性差异。对左、右足迹的足长、足掌宽和足跟宽进行两两相关性分析，从而防止变量间存在高度的共线性。最后，使用Wald统计量检验变量的显著性并建立分析性别的logistic回归模型。

（三）logistic回归模型分析性别的原理。

Logistic回归又称逻辑回归分析，用于处理因变量为定性变量的数据，常用于疾病和财务风险预测等领域。其计算原理如下：假设Y取值为0，1两个值，Y=1的概率为P（Y=1），则m个自变量分别为X1，X2，，……，Xm所对应的logistic回归模型为：或者写为：式中：β0为截距；βi为Xi对应的偏回归系数，也可理解为在控制了其他因素的条件下变量的预测能力。当P值大于0.5时，Y=1；当P值小于0.5时Y=0。基于logistic回归模型的特点，可以建立性别（定性变量）作为因变量，足迹长、足迹掌宽和足迹跟宽作为自变量用于分析性别的logistic回归模型。

二、结果和分析

表1分别给出了男性和女性关于左、右足的各项描述性统计量。由表1可知，男性的左足和右足的足迹长、足迹掌宽、足迹跟宽的均值均大于女性的相应值，这与我们日常认识男性足比女性脚大相一致。

表1 男女赤足迹左右足长、足掌宽和足跟宽的描述性统计量

（一）变量在性别间的差异性检验结果。

为了获取男性和女性足迹中差异较明显的变量，需对足迹长、足迹掌宽和足迹跟宽进行独立样本T检验。经过独立样本T检验，男性和女性的左足和右足的足迹长、足迹掌宽和足迹跟宽的P值均小于0.05（见表2），说明男性和女性的左足和右足的足迹长、足迹掌宽和足迹跟宽均存在显著性差异，此结论与文献[3][4]研究结论一致，从而可以将足迹长、足迹掌宽和足迹跟宽作为三个自变量用于构建分析性别的logistic回归模型。

表2 变量在性别间的独立样本T检验结果

（二）变量在左右足间的差异性检验结果。

为了确定变量在左、右间是否存在显著性差异，从而是否需要分别建立左、右足的logistic回归模型，需要对男性和女性的左、右足相应数据进行配对样本T检验。表3显示了男性和女性的左、右足相应变量间的配对样本T检验结果。由表3可知，在男性中，左足和右足的足迹长和足迹跟宽的P值均大于0.05，足迹掌宽的P值小于0.05，说明在男性中，左足和右足的足迹长和足迹跟宽不存在显著性差异，而足迹掌宽存在显著性差异；在女性中，左足和右足的足迹长和足迹跟宽的P值均小于0.05，足迹掌宽的P值大于0.05，说明在女性中，左足和右足的足迹长和足迹跟宽存在显著性差异，而足迹掌宽不存在显著性差异。这些变量虽然经过统计检验存在显著异性，但是P值并不大，这些差异可能是由于男性和女性在左足和右足间的足底压力分布的不同[5]，进而对足部肌肉产生不同的挤压，从而产生了略微显著的统计差异。由于这些变量在左足和右足间的显著性差异不同，所以分别建立用于分析性别的左足和右足的logistic回归模型是必要的。

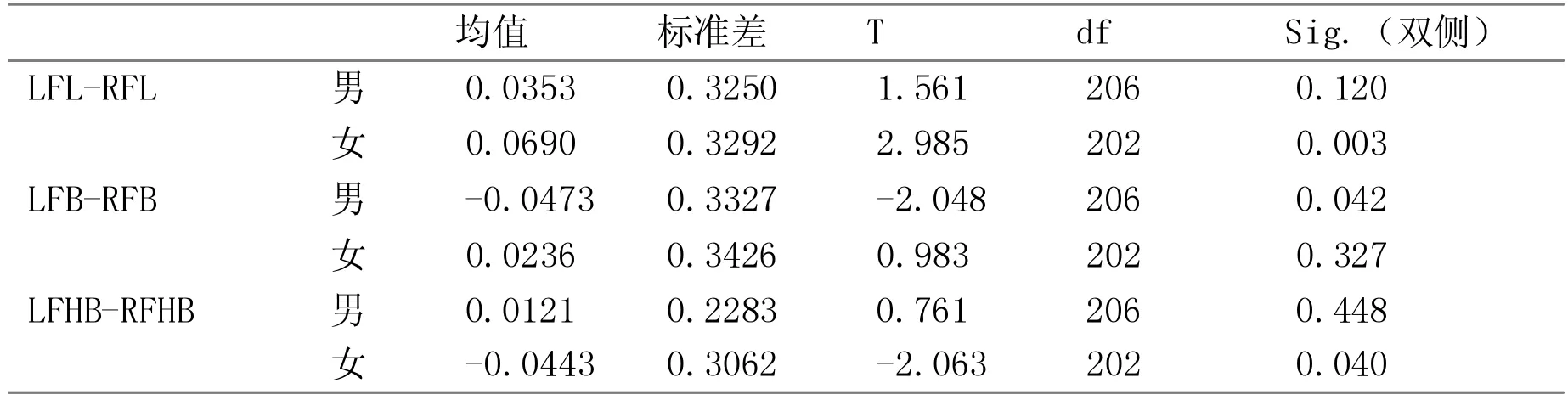
表3 变量在左右足间的配对样本T检验结果

（三）变量间共线性诊断结果。

在建立logistic回归模型前，需要考虑变量间的共线性问题。表4和表5给出了左足和右足的足迹长、足迹掌宽和足迹跟宽的相关性分析结果。由表4和表5可知，左足和右足的足迹长、足迹掌宽和足迹跟宽的Pearson相关性系数r均小于0.8，说明三变量间不存在高度的共线性，可以作为建立logistic回归模型的三个独立变量。

表4 左足变量间的相关性

在α=0.01水平（双侧）上。

表5 右足变量间的相关性

在α=0.01水平（双侧）上。

（四）logistic回归模型的建立。

将男性和女性的左、右足的足迹长、足迹掌宽和足迹跟宽输入SPSS软件建立logistic回归模型，采用向后Wald逐步剔除法确定最终模型。向后Wald逐步剔除法的计算过程是先将所有变量建立回归模型，然后计算每个变量的Wald统计量值，对于不满足显著性水平的变量逐步从回归模型中排除。经计算，SPSS软件对左、右足分别建立一个logistic回归模型（见表6，7）。

表6 左足logistic回归模型

a.在步骤1中输入的变量:LFL，LFB，LFHB；

b.在步骤2中输入的变量:LFL，LFB。

表7 右足logistic回归模型

a.在步骤1中输入的变量:RFL，RFB，RFHB；

b.在步骤2中输入的变量:RFL，RFB。

1．左足logistic回归模型。由表6可知，步骤1所建立的左足回归模型中变量LFHB的Wald检验的显著性水平等于0.638大于0.05，说明在利用回归模型对性别进行预测时，变量LFBH对性别预测的贡献较小，即变量LFHB与性别关联性较小，故将其排除获得步骤2建立的左足回归模型：

步骤2建立的回归模型中变量的Wald检验的显著性水平均小于0.05，说明在利用所建立的回归模型对性别进行预测时，变量LFL、LFB对性别预测的贡献较大，即变量LFL、LFB与性别的关联性较大，可以有效预测和解释性别。

将男性和女性左足的相应数据分别代入到以上步骤2建立的左足logistic回归模型中进行预测，当P值大于0.5时预测为女性，当P值小于0.5时预测为男性。步骤2建立的左足logistic回归模型预测结果见表8。

表8 左足步骤2回归模型的预测结果

a.切割值为0.500。

由表6可知，步骤2建立的左足logistic回归模型具有统计学意义，并且，由表8可知，步骤2建立的回归模型对男性左足赤足迹预测正确的百分比为89.9%，对女性左足赤足预测正确的百分比为87.7%，对左足赤足迹性别预测正确的总百分比为88.8%。

2.右足logistic回归模型。同理，由表7可知，步骤1所建立的右足回归模型中变量RFHB的Wald检验的显著性水平等于0.844大于0.05，说明在利用回归模型对性别进行预测时，变量RFHB对性别预测的贡献较小，即变量RFHB与性别关联性较小，故将其排除获得步骤2建立的右足回归模型：

步骤2建立的回归模型中变量的Wald检验的显著性水平均小于0.05，说明在利用所建立的回归模型对性别进行预测时，变量RFL、RFB对性别预测的贡献较大，即变量RFL、RFB与性别存在关联性较大，可以有效预测和解释性别。

将男性和女性右足的相应数据分别代入到步骤2建立的右足logistic回归模型中进行预测，当P值大于0.5时预测为女性，当P值小于0.5时预测为男性。步骤2建立的右足logistic回归模型预测结果见表9。

表9 右足步骤2回归模型的预测结果

a.切割值为0.500

由表7可知，步骤2建立的logistic回归模型具有统计学意义，并且，由表9可知步骤2所建立的回归模型对男性右足赤足迹预测正确的百分比为89.4%，对女性右足赤足迹预测正确的百分比为90.6%，对右足赤足迹性别预测正确的总百分比为90.0%。

三、结论

本文通过提取男、女赤足迹中足长、足掌宽和足跟宽，用独立样本T检验比较了男性和女性在赤足迹中的足长、足掌宽和足跟宽的统计学差异，用配对样本T检验比较了左足和右足在赤足迹中的足长、足掌宽和足跟宽的统计学差异，用Wald逐步剔除法分别建立了左、右足关于足迹长和足迹掌宽的logistic回归模型。所建立的左、右足logistic回归模型对样本进行性别预测，预测正确的百分比分别为88.8%、90.0%，均具有较高的预测准确率，说明建立的logistic回归模型拟合度较好，可以为现场勘验人员对现场赤足迹的性别分析提供参考。同时，在办案的实际工作中，现场勘验人员在运用上述模型时，也应结合足型特征和案件的其他情况进一步提高对性别分析的准确率，从而为分析犯罪嫌疑人人身特点提供更有力的依据。

[1]尚金萍.女性犯罪增多的性别视角浅析[J].山西警官高等专科学校学报，2010，(3):18-21.

[2]史力民.足迹学[M].北京:中国人民公安大学出版社，2007.

[3]汤澄清.利用足迹足型特征分析性别的研究[J].山西警官高等专科学校学报，2009，(3):78-80.

[4]Jaydip Sen,等.Sex Estimation from Foot Dimensions in an Indigenous Indian Population[J].Forensic Sic，2011，56:S148-S153.

[5]张腾丹，等.青年大学生行走步态足底区域压力特征变化的研究[J].辽宁警察学院学报，2016，1:85-91.

[6]荣泰生.SPSS与研究方法[M].大连:东北财经大学出版社，2012.

[7]郭志刚.社会统计分析方法[M].北京:中国人民大学出版社，2015.

[8]DM Fessler，等.Sexual dimorphism in foot length proportionate to stature[J].Taylor&Francis，2005，32(1):44-59.

[9]Jacqueline Domjanic,等.A Combined Morphometric Analysis of Foot Form and Its Association with Sex，Stature，and Body Mass[J].American Journal of Physical Anthropology，2015，157(4):582-291.

[10]Kewal Krishan，等.Sex Determination from Hand and Foot Dimensions in a North Indian Population[J].Forensic Sic，2011，56 (2):453-459.

[11]Naomi Hemy,等.Sex estimation using anthropometry of feet and footprints in a Western Australian population[J].Forensic SciInt，2013，231(2013):402e1-102e6.

Gender-analysis of Bare Footprints Based on Logistic Regression Model

JI Ruijun,TANG Cheng-qing,WANG Ming-yue

t:Objective:To investigate the gender of the footprints left at the crime scene.Methods:Select the footprint length,footprint width and footprint heel width as independent variables,and gender as the dependent variable,then establish the logistic regression model.Sample:Collected 410 men and women left and right bare footprint samples(male 207,female,203),and the characteristics of footprint length,footprint width and footprint are measured.Conclusion:The prediction’s accuracy of the model acquired by left bare footprints on gender was 88.8%,and the right footprints was 90.0%.Gender prediction has a higher accuracy.On certain conditions,the mathematical model can provide a reference for the crime scene examiner for gender analysis by bare footprints.

Bare footprint;Gender；Footprint Length;Footprint width；Footprint heel width;Logistic regression

D981.912

：A

：1674-5612（2017）01-0062-07

（责任编辑：吴良培）

2017-01-12

姬瑞军，（1991-），男，河南鹤壁人，中国刑事警察学院硕士生，研究方向：痕迹检验学；汤澄清，（1969-），男，辽宁沈阳人，硕士，中国刑事警察学院教授，研究方向：痕迹检验学；王明月，（1993-），男，山东滨州人，中国刑事警察学院硕士生，研究方向：痕迹检验学。