分段压裂裂缝扩展规律及其对导流能力的影响

包劲青，刘合，张广明，金娟，程威，刘建东（1. 中国石油勘探开发研究院，北京 100083；2. 中国石油天然气集团公司采油采气重点实验室，北京 100083）

分段压裂裂缝扩展规律及其对导流能力的影响

包劲青1, 2，刘合1, 2，张广明1, 2，金娟1, 2，程威1, 2，刘建东1, 2
（1. 中国石油勘探开发研究院，北京 100083；2. 中国石油天然气集团公司采油采气重点实验室，北京 100083）

基于前人的研究并充分考虑裂缝间的相互干扰以及各种摩擦效应对排量分配的影响，提出了模拟水平井分段压裂中裂缝同步扩展的全耦合有限元方法，利用该方法研究了裂缝扩展规律及其对导流能力的影响。模拟结果表明，虽然各裂缝的排量分配率均沿平均裂缝分配率上下波动，但缝间干扰导致裂缝扩展速度各不相同，部分裂缝甚至短暂地停止扩展。短裂缝内的流体净压力普遍比长裂缝高，但压力梯度更小。缝间流体净压力的差异使长裂缝在远离井口的位置发生颈缩，在井口和颈缩处长裂缝可能发生砂堵。分段压裂裂缝扩展规律将对导流能力产生不利影响：①短裂缝因支撑剂沉降较快弱化了自身的导流能力；②长裂缝因在井口发生砂堵丧失导流能力；③长裂缝在颈缩处发生砂堵降低了导流能力。图10参30

水平井；分段压裂；缝间干扰；裂缝扩展；裂缝导流能力

引用：包劲青, 刘合, 张广明, 等. 分段压裂裂缝扩展规律及其对导流能力的影响[J]. 石油勘探与开发, 2017, 44(2): 281-288.

BAO Jinqing, LIU He, ZHANG Guangming, et al. Fracture propagation laws in staged hydraulic fracturing and their effects on fracture conductivities[J]. Petroleum Exploration and Development, 2017, 44(2): 281-288.

0 引言

随着非常规油气资源开发的兴起[1]，水平井钻井技术和分段分簇的水力压裂技术在油气工业中的作用愈加重要。分段压裂中段内同步扩展的裂缝之间存在强烈的相互作用，这些相互作用导致裂缝形态各异，进而增产效果各不相同。实际生产数据分析表明，30%甚至更多的射孔簇会因为导流能力不足而没有增产效果[2]。迄今为止，由于对水平井中分段压裂的裂缝扩展规律缺乏足够的认识，业界对部分裂缝导流能力不足的机理尚不甚清楚，因而进行水平井分段压裂优化设计时缺乏可靠的依据。研究分段压裂中裂缝的扩展规律及其对裂缝导流能力的影响具有重要的工程意义。

以位移不连续法（边界元方法[3]）为基础，国内外学者在裂缝同步扩展方面做了大量的研究工作。Peirce 等[4]研究了裂缝的同步扩展，提出分段压裂中变簇距设计有利于提高裂缝群的整体导流能力。Lecampion等[5]考虑了孔眼摩阻对流量的调节作用，提出无量纲参数以判断起主导作用的排量分配机制，并讨论了在分段压裂的早期阶段不同主导机制作用下排量分配和裂缝扩展速度的规律。Lecampion等[5]的研究表明，如果射孔不能提供足够的摩阻，部分裂缝会因为分配的排量不足而停止扩展。Kresse等[6]基于改进的位移不连续方法研究裂缝的同步扩展，发现边裂缝起主导作用。Sesetty等[7]研究了先导裂缝对同步扩展裂缝的影响，指出先导裂缝引起的边界条件对裂缝形态有重要作用。胥云等[8]讨论了多裂缝应力干扰的作用范围。

近些年众多学者采用有限元方法研究水力压裂。对于单一裂缝，Hunsweck等[9]模拟了存在流体滞后区而且无滤失时裂缝的扩展；Gordeliy等[10]用扩展有限元方法研究了不同能量耗散机理和不同流体滞后区情况的裂缝扩展；Bao等[11]研究了不同能量耗散机理和不同滤失情况下裂缝的扩展，并引入刚度凝聚技术以加快模拟速度[12]。这些数值模型得到近些年提出的解析解[13-18]的验证。对于多裂缝，Dahi Taleghani[19]基于扩展有限元研究裂缝同步扩展，发现当裂缝长度大于裂缝间距时，裂缝间存在强烈的相互作用；张广明等[20]基于孔隙介质理论研究了裂缝同步扩展时最小主应力方向发生改变的条件；潘林华等[21]基于损伤力学探讨了应力干扰对同步扩展裂缝的影响。

尽管在多裂缝扩展的模拟方面已有众多的研究工作，但对于分段压裂裂缝的扩展规律和裂缝导流能力不足的根源并没有完全揭示，这方面仍需要细致深入的研究。本文在文献[11]工作的基础上，充分考虑裂缝间的相互干扰以及各种摩擦效应等情况，提出模拟水平井分段压裂中裂缝同步扩展的全耦合有限元方法。利用该方法研究水平井分段压裂中同步扩展的裂缝在扩展速度、排量分配、裂缝宽度和流体净压力等方面的规律，并分析这些扩展规律对裂缝导流能力的影响，为水平井分段压裂的优化设计提供可靠的依据。

1 物理和数学模型

水平井分段压裂的工作原理是通过段内各簇的射孔设计（见图1a），使通过射孔孔眼的流体在井筒周围经受与簇内流量正相关的摩擦阻力，在摩擦阻力对排量分配的调节作用下期望段内各簇被压开以达到增产效果。数值模拟时通常认为每一簇射孔会产生一条裂缝[4-5,19]。如图1b所示，沿水平井筒内流体流动方向，裂缝从1至N依次编号。为简化计算，本文假设裂缝扩展方向始终垂直于远场最小主应力方向。研究表明[6-7]当远场最大与最小主应力之间的差值较大时，该假设是合理的。

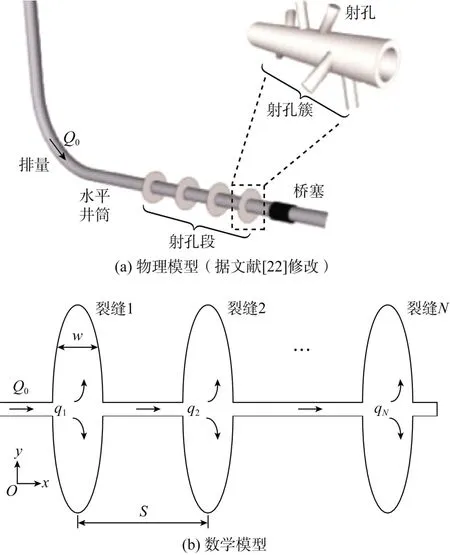
图1 水平井分段压裂物理和数学模型

影响裂缝扩展的数学方程有段内流体质量守恒方程、裂缝宽度与流体压力的关系方程、井周摩阻方程、井筒内缝间流体压降方程、缝内流体质量守恒方程、流动方程和滤失方程。忽略流体的可压缩性和井筒半径的影响，以平面应变模型为基础并以水平井延伸方向为x方向，各方程可表述如下。

如图1b所示，段内流体的质量守恒方程为：

水平井筒内，任意两相邻裂缝处的流体压力关系式为：

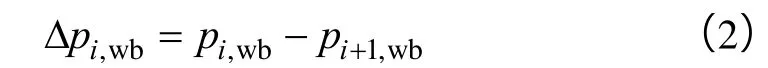
缝内任意一点流体的质量守恒方程为：

裂缝在井筒处的流量为qi/h。如果流体为牛顿流体，则（3）式中q可表示为[23]：

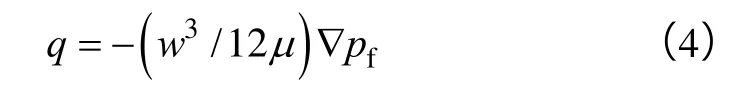
本文应用Carter滤失模型[24]，其滤失量表达式为：

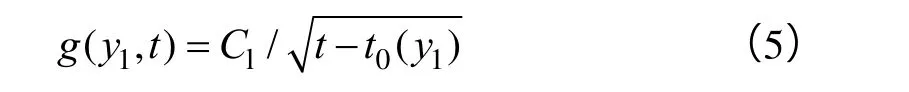
裂缝的井周摩阻方程为：

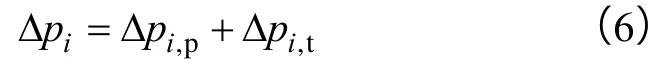
其中Δpi,p的计算公式为实验拟合公式[25]：

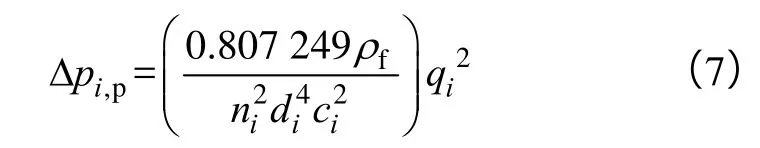
（7）式括号内的表达式为文献[5]所定义的射孔摩阻系数。

根据文献[26-27]，裂缝宽度的广义积分形式为：

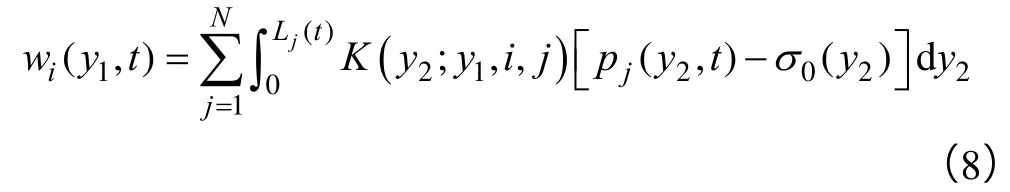
裂缝的扩展准则为：

2 有限元方法

从物理和数学模型可知，分段压裂中待求量为分配排量、裂缝宽度和裂缝内的流体压力。求解结果需要满足（1）式和（2）式的约束。岩体介质经过有限单元离散后可以得到如下方程[28]：

由（10）式，应用刚度凝聚技术[12]可得：

K是稠密矩阵，反映了裂缝宽度对流体压力的全局依赖性和裂缝间的相互作用。（11）式是（8）式的离散格式。与边界元相比，用有限元求（8）式的离散格式可以避免寻找核函数[14]。

由（3）式—（5）式可知缝内流体的有限元方程为[29]：

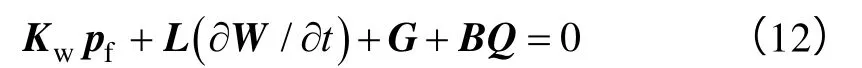
采用隐式积分，由（12）式可得：

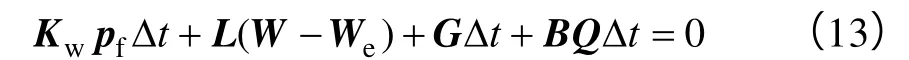
由于iq为待求量，因此耦合方程（11）和（13）因未知量大于其维数而不可解。在文献[11]工作的基础上，本文采用迭代方法求解耦合方程（11）和（13）。首先假设符合（1）式的裂缝试分配量iq并求解耦合方程（11）和（13）；然后计算水平井筒内各裂缝处的流体压力并判断它们是否近似满足下式：

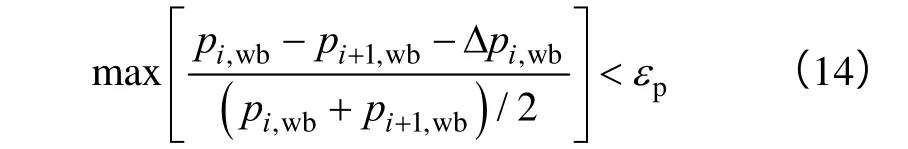
（14）式是对（2）式的近似处理。若不满足（14）式，在满足（1）式的前提下调整试分配量iq直至（14）式完全满足为止。上述迭代方法中（1）式得到完全满足，而（2）式得到了近似处理。

虽然文献[11]的方法也能模拟多裂缝的同步扩展，但需要指定排量在每条裂缝的分配量，因此不能考虑各种摩擦效应对排量分配的调节作用，进而不能模拟水平井的分段压裂。本文采用迭代方法实现了水平井分段压裂中多裂缝同步扩展的模拟。

3 方法检验

在模拟单一裂缝方面有限元方法已经得到了理论解的完全验证[11]。本文从两方面检验分段压裂模拟方法：①比较本文方法与文献[5]发现的裂缝扩展规律是否相似；②核对本文方法的模拟结果是否符合水平井分段压裂的典型特征。

本文采用平面应变模型，文献[5]采用轴对称模型。检验的平面应变模型内有 3条水平裂缝，其初始长度均为2 m，高度均为100 m。裂缝内的初始流体净压力均为0.1 MPa。和轴对称模型一样，本文模型忽略井筒摩阻和弯曲摩阻，而且不考虑滤失的影响。另外，本文模型和轴对称模型具有相同的材料参数和部分压裂设计参数，其中岩石的弹性模量为25 GPa，泊松比为0.2，裂缝间距为25 m，岩石断裂韧性为1.2 MPa·m1/2，远场最小围压为37.2 MPa，流体动力黏度为5.0×10－9MPa·s，射孔摩阻系数为1 000 MPa·s2/m6。文献[5]中排量从0迅速增加至0.159 m3/s然后保持不变，而本文模型中排量一直为0.159 m3/s，由文献[5]可知此时平均单缝分配排量能够提供足够的射孔摩阻。在裂缝扩展路径上平面应变模型有限单元的特征尺寸为1 m，在远离扩展路径处有限单元的特征尺寸为25 m。

图 2是本文（平面应变）模型和轴对称模型得到的排量分配图和裂缝半长、裂缝半径随时间变化图。由于两个模型的初始排量不同，所以本文模型起初的排量分配情形与文献[5]有较大区别（见图 2a）。另外文献[5]采用轴对称模型而本文采用平面应变模型，所以裂缝扩展速度也不同（见图2b）。当平均单缝分配排量能够提供足够的射孔摩阻时，由图2a可知，各裂缝的流量均接近于平均单缝分配排量，并随着裂缝的扩展有波动的趋势。由图2b可知，当流量接近一致而且裂缝半长或半径在裂缝间距的 2倍以内时，每个模型中各裂缝扩展速度没有非常明显的差异。尽管两个模型具有不同的初始边界条件和裂缝扩展模式，但是它们的裂缝扩展规律相同。

分段压裂的典型特征是排量在各裂缝动态分配，而且当忽略井筒摩阻时井筒内各点的流体压力应完全一致。这两个特征可以检验本文方法能否模拟分段压裂。由图2a可知本文模型中排量在各个裂缝中动态分配；由图3可知井筒内各裂缝处的流体压力极为接近。说明本文方法模拟结果符合分段压裂的典型特征。

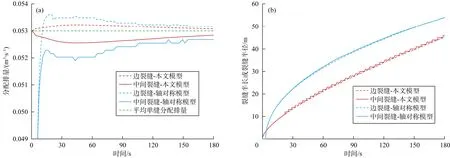
图2 裂缝流量（a）和裂缝半长或半径（b）随时间变化曲线

4 裂缝扩展规律及其影响

数值模型考虑段内分簇数目即裂缝数目N等于4、5、6等3种情况，并假设裂缝沿水平井筒对称，裂缝间距为20 m。裂缝初始条件与方法检验时模型中裂缝的初始条件相同。当有裂缝半长达到150 m时终止模拟。图4为N等于6时水平井附近的有限元网格，其坐标原点定义在裂缝3和4之间水平井筒段的中间位置上。

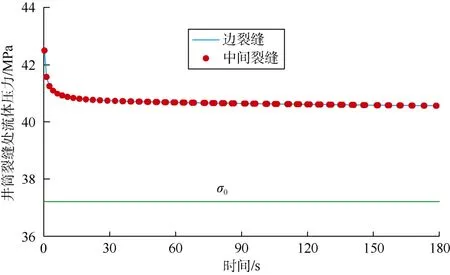
图3 本文模型中井筒各裂缝处的流体压力

图4 N等于6时井筒附近的有限元网格示意图

通常井筒摩阻远小于孔眼摩阻和弯曲摩阻，另外因弯曲摩阻和孔眼摩阻具有相同的数学形式和功能，因此模型仅考虑孔眼摩阻的影响。数值模型中岩石的弹性模量为18 GPa，泊松比为0.2，每簇射孔数目均为20，孔眼直径均为0.008 8 m，孔眼流量系数均为0.9，岩石断裂韧性为 1.5 MPa·m1/2，远场最小围压为 40 MPa，流体动力黏度为1.0×10-9MPa·s，平均单缝排量为 0.016 m3/s，裂缝高度为 100 m，滤失系数为5.0×10-6m/s1/2，流体密度为1 000 kg/m3。在裂缝扩展路径上有限单元的特征尺寸为1 m，在远离扩展路径处有限单元的特征尺寸为25 m。

4.1 排量分配

图5是排量在各裂缝的分配率。由图5可见，通过一定的射孔设计可保证排量能够顺利分配到各个裂缝，不会出现缝内流体回流或者排量停止分配到部分裂缝的现象，这与文献[5]的结论一致。此时各裂缝的排量分配率沿平均单缝分配率上下波动且波动幅度逐渐减小。由于（1）式的约束，各排量分配率会存在如图 5所示的此增彼减或此减彼增的现象。由于裂缝的位置不同，因此排量分配率的变化幅度也各不相同。

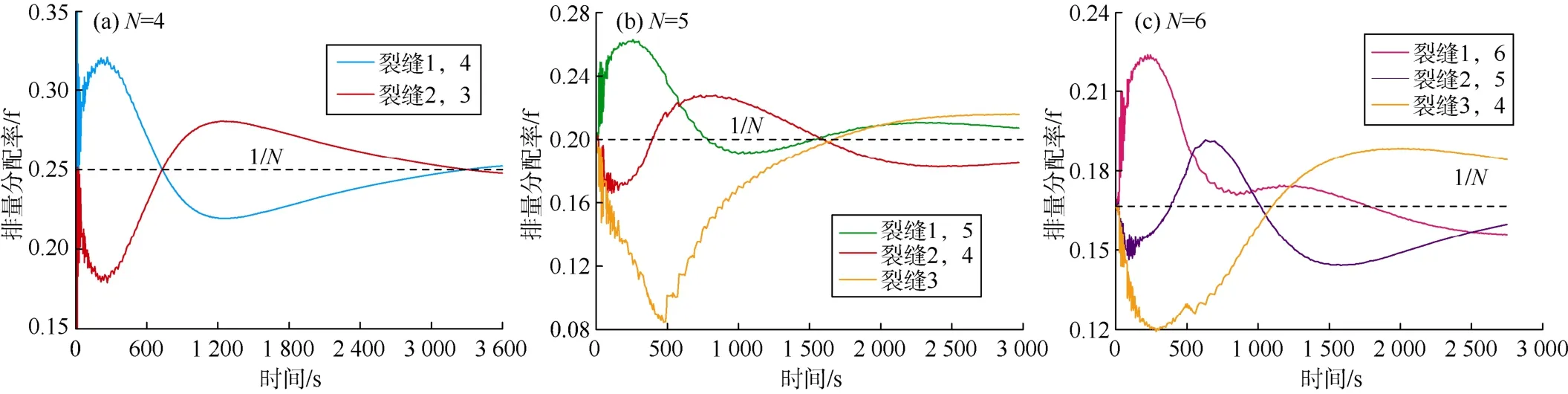
图5 排量在各裂缝的分配率

4.2 裂缝长度

图6为各裂缝半长图。由图6可见，在裂缝扩展初期由于裂缝较短它们间的相互干扰较弱，各裂缝扩展速度相近。随后由于裂缝间的相互干扰增强，裂缝扩展速度出现显著差异。尤其是N等于5和6时长度差异较大，中间裂缝最终长度远小于其他裂缝。由图6b和6c可见，受到周围裂缝的抑制作用，部分裂缝甚至短暂地停止扩展。由于排量不断分配到这些裂缝（见图5），并且其他裂缝扩展对岩体产生削弱作用，短裂缝会突破其他裂缝的抑制而继续扩展。

图6 裂缝半长分布图

4.3 裂缝宽度

图 7为近井筒处裂缝宽度图。同样在裂缝扩展初期各裂缝在近井筒处宽度相近，随后差异逐渐显著。对于N等于5和6这两种情况，压裂后不久在井筒处长裂缝一直比短裂缝窄。对于N等于4这种情况，相当长时间内在井筒处长裂缝比短裂缝窄。通常认为，当裂缝宽度小于支撑剂粒径的 3倍时就会有砂堵的风险[30]。若在压裂开始20 min后加入粒径0.212 mm（70目）的支撑剂，由图 7可见，长裂缝均有一定的砂堵风险，而且对于N等于5和6这2种情况井口砂堵风险长期存在。

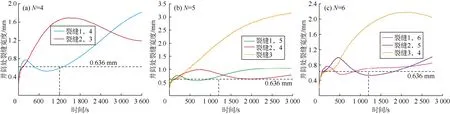
图7 近井筒处各裂缝宽度分布图

图8为2 700 s时裂缝宽度分布图。由图8可见，短裂缝普遍比长裂缝宽，另外长裂缝形态完全不同于短裂缝，而且长裂缝在远离井口的位置出现颈缩。原因在于：①长裂缝对岩体的切削作用更为强烈，因此长裂缝更容易受到短裂缝的干扰而变形；②在裂缝中间部位短裂缝内的流体净压力远高于长裂缝的流体净压力（见图9），因此长短裂缝间的净应力差异不利于长裂缝宽度的发展。两方面的因素导致长裂缝受到挤压作用而出现颈缩。若采用粒径0.212 mm（70目）的支撑剂，有些裂缝有可能会在中前部发生砂堵，而有些裂缝可能会在中后部发生砂堵（见图8）。因此颈缩现象意味着在裂缝端部以外也可能发生砂堵。实际工程中这种砂堵的负面影响包括两个方面：一是迫使裂缝往高度和宽度方向而非长度方向扩展，二是它会阻塞裂缝使其不能发挥应有的导流作用。

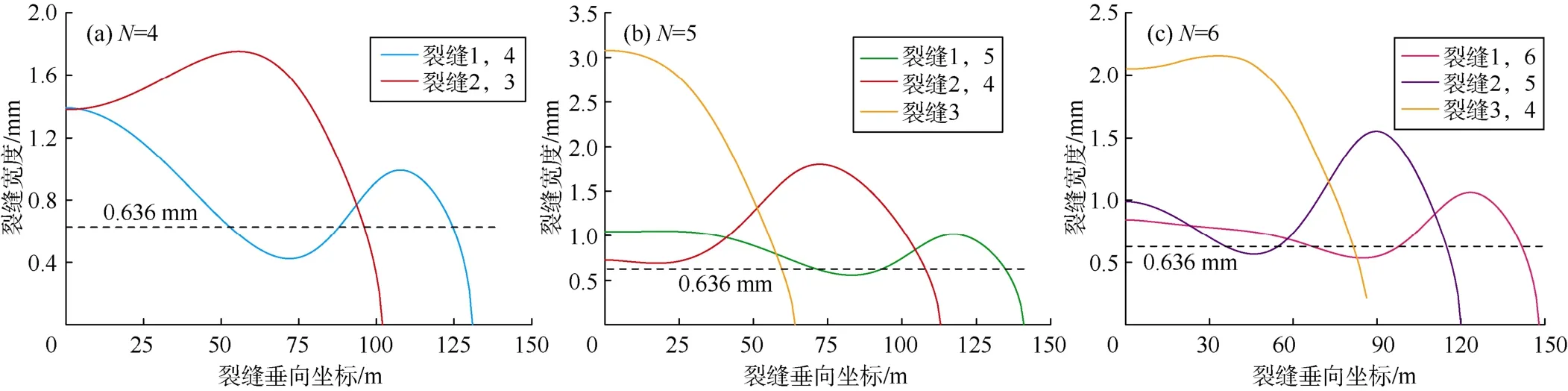
图8 2 700 s时裂缝宽度分布图

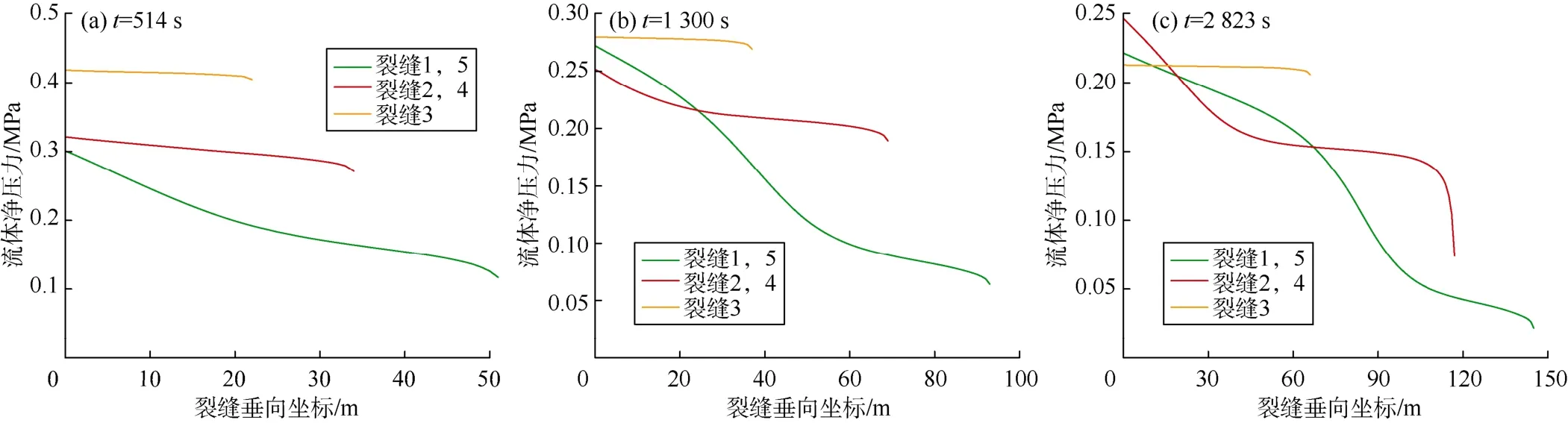
图9 N等于5时不同时刻流体净压力分布图

4.4 流体净压力

图9为N等于5时在3个不同时刻流体的净压力分布。由图 9可见，短裂缝的流体净压力大多比长裂缝高。短裂缝因宽度较大，流体流动所需要的压力梯度更小（见（4）式），因此整个压裂过程中短裂缝的净压力分布更为平缓。N等于4和6时也发现同样的现象。较小的压力梯度意味着短裂缝中支撑剂更容易发生沉降。支撑剂沉降削弱了短裂缝的导流能力，因为短裂缝的上部因缺乏支撑剂的有效支撑在注入液回流后会发生闭合，再者短裂缝的下部因支撑剂的淤积阻塞了油气流动的通道。

4.5 裂缝形态演化

由于忽略了井筒摩阻，理论上裂缝群应该具有对称性。以N等于6为例（见图4），裂缝1和裂缝6应沿 y轴相互对称，而且它们应具有相同的扩展速度和压力分布。由图5—图9可见，3种分簇情况裂缝群的对称性得到了模拟结果的印证。

图10为N等于6时裂缝1，2，3在4个不同时刻的形态。图中裂缝在x方向放大了10 000倍。由图10可见，在压裂初期由于裂缝间的相互干扰较弱，因此裂缝形态差异较小而且没有颈缩。但是随着裂缝间的相互干扰增强裂缝形态差异越来越明显，裂缝 1和 2出现颈缩，并且随着裂缝的扩展颈缩位置不断移动。由于裂缝间的推挤作用，裂缝1和2整体向外侧极为轻微地移动，并且轻微扭曲。N等于4和5时也观察到同样的现象。

用方法检验时模型的参数模拟N等于4、5、6等3种不同分簇情况的分段压裂时，同样发现裂缝排量分配率波动、长裂缝在井周宽度较窄、短裂缝净压力分布平缓以及长裂缝发生颈缩等重要现象。这说明由于裂缝间强烈的相互作用，单一裂缝模型的诸多扩展规律在分段压裂中已不适用。

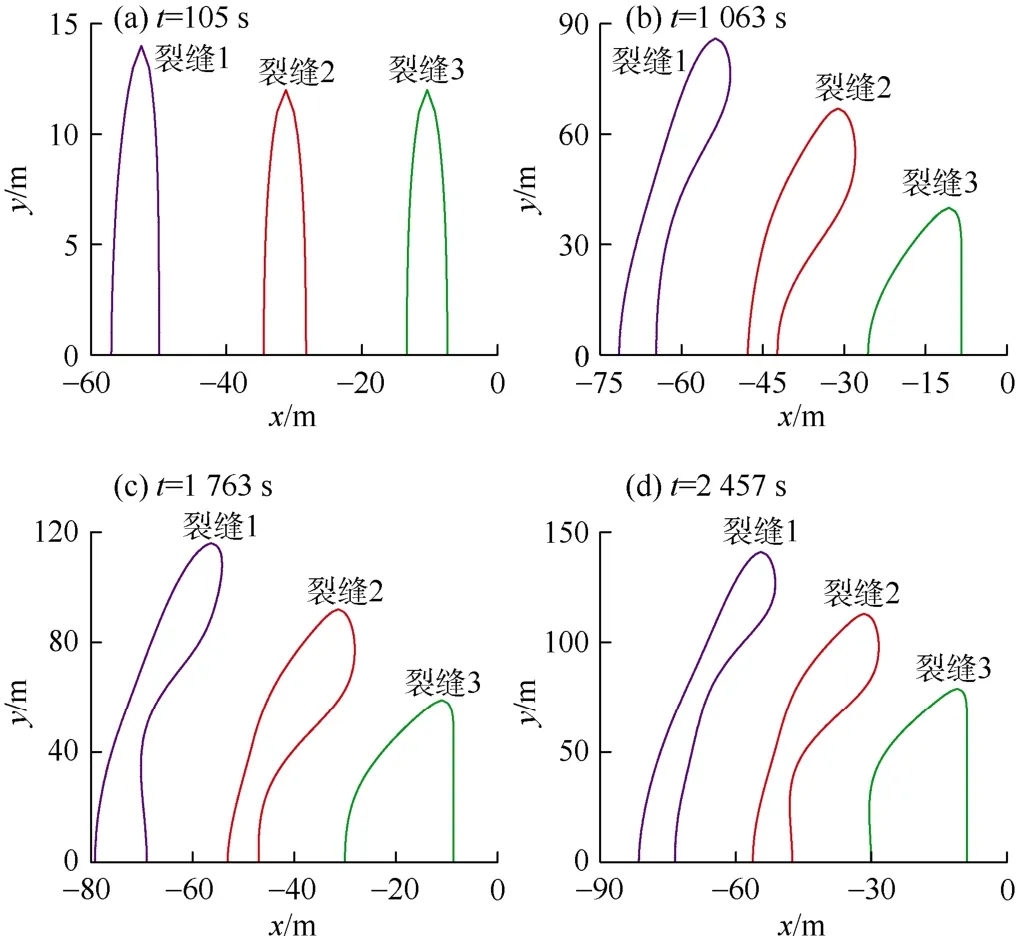
图10 N等于6时不同时刻3条裂缝的形态

分段压裂裂缝的各种扩展规律存在紧密的内在联系。裂缝之间的相互干扰作用导致它们的扩展速度各不相同。因此当裂缝的排量分配率接近一致时，部分裂缝因为长度短、滤失少必然会比其他裂缝宽。这意味着这些短裂缝内流体净压力会更高而且其分布会更平缓。

裂缝的这些扩展规律将对导流能力产生不利的影响：①短裂缝的压力分布平缓，其内支撑剂会快速沉降，导致短裂缝因上部缺乏有效的支撑、下部支撑剂发生淤积而削弱了导流能力；②长裂缝由于在近井处宽度较窄而有砂堵的风险，从而丧失导流能力；③长裂缝在扩展过程中会颈缩，从而改变裂缝的主导扩展方向并降低了裂缝的导流能力。

5 结论

在文献[11]工作的基础上，提出了分段压裂的全耦合有限元方法，方法充分考虑了裂缝间的相互作用以及各种摩擦效应等。运用该方法模拟了不同分簇数目的水平井分段压裂。研究表明，可以通过一定的射孔设计保证排量能够顺利分配到各个裂缝，但是由于裂缝间的相互作用导致以往单一裂缝的扩展规律在分段压裂中已不适用。分段压裂中会出现窄井筒裂缝宽度、平缓的压力分布和颈缩等现象。这些现象会对裂缝导流能力产生不利的影响。

符号注释：

B——将Q转换成等效节点流量的矩阵，无因次；ci——第i簇射孔的孔眼流量系数，无因次；C——远场最小围压引起的裂缝闭合量矢量，m；Cl——滤失系数，m/s1/2；di——第i簇射孔的孔眼直径，m；F1——流体压力的等效节点力组成的矢量，106N；F2——远场最小围压的等效节点力组成的矢量，106N；g——流体滤失量，m/s；g（y1，t）——t时刻流体在 y=y1处的滤失量，m/s；G——滤失量的影响矢量，m2/s；h——裂缝高度，m；K——积分核函数，m/MPa；K——W和pf的关系矩阵，m/MPa；KI——裂缝尖部应力强度因子，MPa·m1/2；KIC——岩石的断裂韧性，MPa·m1/2；Ku——岩体的刚度矩阵，106N/m；Kw——裂缝内流体的刚度矩阵，m2/(MPa·s)；L——裂缝长度矩阵，m；Lj（t）——t时刻第j条裂缝的长度，m；ni——第i簇的射孔数目；N——分簇总数目；pi,wb——水平井筒在第i条裂缝处的流体压力，MPa；pf——流体压力，MPa；pj（y2，t）——t时刻第 j条裂缝在y=y2处的流体压力，MPa；pf——流体压力矢量，MPa；q——面流量，m2/s；qi——第i条裂缝的分配排量，m3/s；Q——由qi/h（i=1，2，…，N）组成的矢量，m2/s；Q0——排量，m3/s；S——簇间距，m；t——时间，s；t0（y1）——流体前缘达到y=y1处的时间，s；U——节点位移组成的矢量，m；w——裂缝宽度，m；wi（y1，t）——第i条裂缝t时刻在y=y1处的宽度，m；W——缝宽度组成的矢量，m；We——上一平衡步裂缝宽度矢量，m；x，y——直角坐标系，m；y1，y2——y方向上的坐标，m；Δpi——第i条裂缝的井周摩阻，MPa；Δpi,p——第i条裂缝的孔眼摩阻，MPa；Δpi,t——第i条裂缝的弯曲摩阻，MPa；Δpi,wb——井筒内两相邻裂缝间由井筒摩擦引起的压力损失，MPa；Δt——计算时间步长，s；εp——流体压力容许差异因子，取 10-6，无因次；μ——流体的动力黏度，MPa·s；ρf——注入流体密度，kg/m3；σ0（y2）——远场y=y2处的最小围压，MPa。下标：i，j——裂缝编号。

[1] 邹才能, 董大忠, 王玉满, 等. 中国页岩气特征、挑战及前景（一）[J]. 石油勘探与开发, 2015, 42(6): 689-701. ZOU Caineng, DONG Dazhong, WANG Yuman, et al. Shale gas in China: Characteristics, challenges and prospects (Ⅰ)[J]. Petroleum Exploration and Development, 2015, 42(6): 689-701.

[2] MILLER C, WATERS G, RYLANDER E. Evaluation of production log data from horizontal wells drilled in organic shales[R]. SPE 144326, 2011.

[3] CROUCH S L, STARFIELD A M. Boundary element methods in solid mechanics[M]. London: Unwin Hyman, 1990.

[4] PEIRCE A, BUNGER A. Interference fracturing: Non-uniform distributions of perforation clusters that promote simultaneous growth of multiple hydraulic fractures[R]. SPE 172500, 2015.

[5] LECAMPION B, DESROCHES J. Simultaneous initiation and growth of multiple radial hydraulic fractures from a horizontal wellbore[J]. Journal of the Mechanics and Physics of Solids, 2015, 82(2): 235-258.

[6] KRESSE O, WENG X, GU H, et al. Numerical modeling of hydraulic fractures interaction in complex naturally fracturedformations[J]. Rock Mechanics and Rock Engineering, 2013, 46(3): 555-568.

[7] SESETTY V, GHASSEMI A. A numerical study of sequential and simultaneous hydraulic fracturing in single and multi-lateral horizontal wells[J]. Journal of Petroleum Science and Engineering, 2015, 132: 65-76.

[8] 胥云, 陈铭, 吴奇, 等. 水平井体积改造应力干扰计算模型及其应用[J]. 石油勘探与开发, 2016, 43(5): 780-786, 798. XU Yun, CHEN Ming, WU Qi, et al. Stress interference calculation model and its application in volume stimulation of horizontal wells[J]. Petroleum Exploration and Development, 2016, 43(5): 780-786, 798.

[9] HUNSWECK M J, SHEN X Y, ADRIAN J L. A finite element approach to the simulation of hydraulic fractures with lag[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(9): 993-1015.

[10] GORDELIY E, PEIRCE A. Coupling schemes for modeling hydraulic fracture propagation using the XFEM[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 253(1): 305-322.

[11] BAO J Q, FATHI E, AMERI S. Uniform investigation of hydraulic fracturing propagation regimes in the plane strain model[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 39(5): 507-523.

[12] BAO J Q, FATHI E, AMERI S. A coupled finite element method for the numerical simulation of hydraulic fracturing with a condensation technique[J]. Engineering Fracture Mechanics, 2014, 131(1): 269-281.

[13] ADACHI J, DETOURNAY E. Plane strain propagation of a hydraulic fracture in a permeable rock[J]. Engineering Fracture Mechanics, 2008, 75(16): 4666-4694.

[14] BUNGER A P, DETOURNAY E, GARAGASH D I. Toughnessdominated hydraulic fracture with leak-off[J]. International Journal of Fracture, 2005, 134(2): 175-190.

[15] GARAGASH D I. Plain-strain propagation of a fluid-driven fracture during injection and shut-in: Asymptotics of large toughness[J]. Engineering Fracture Mechanics, 2006, 73(4): 456-481.

[16] HU J, GARAGASH D I. Plane-strain propagation of a fluid-driven crack in a permeable rock with fracture toughness[J]. ASCE Journal of Engineering Mechanics, 2010, 136(9): 1152-1166.

[17] GARAGASH D I, DETOURNAY E. Plane-strain propagation of a fluid-driven fracture: Small toughness solution[J]. Journal of Applied Mechanics, 2005, 72(6): 916-928.

[18] GARAGASH D I. Propagation of a plane-strain hydraulic fracture with a fluid lag: Early-time solution[J]. International Journal of Solids and Structures, 2006, 43(18): 5811-5835.

[19] DAHI TALENGHTANI A. Modeling simultaneous growth of multi-branch hydraulic fracturing[R]. San Francisco: American Rock Mechanics Association, 2011.

[20] 张广明, 刘勇, 刘建东, 等. 页岩储层体积压裂的地应力变化研究[J]. 力学学报, 2015, 47(6): 965-972. ZHANG Guangming, LIU Yong, LIU Jiandong, et al. Research on the geostress change of shale reservoir volume fracture[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(6): 965-972.

[21] 潘林华, 张士诚, 程礼军, 等. 水平井“多段分簇”压裂簇间干扰的数值模拟[J]. 天然气工业, 2014, 34(1): 74-79. PAN Linhua, ZHANG Shicheng, CHENG Lijun, et al. A numerical simulation of the inter-cluster interference in multi-cluster staged fracturing for horizontal wells[J]. Natural Gas Industry, 2014, 34(1): 74-79.

[22] LECAMPION B, DESROCHES J. Simultaneous initiation of multiple transverse hydraulic fractures from a horizontal well[R]. Minneapolis: American Rock Mechanics Association, 2014.

[23] BATCHELOR G K. An introduction to fluid dynamics[M]. Cambridge: Cambridge University Press, 1967.

[24] CARTER R D. Optimum fluid characteristics for fracture extension[M]//HOWARD G, FAST C. Drilling and production practices. Tulsa: American Petroleum Institute, 1957.

[25] CRUMP J, CONWAY M. Effects of perforation-entry friction on bottomhole treating analysis[R]. SPE 15474, 1988.

[26] ECONOMIDIES M J, NOLTE K G. Reservoir stimulation[M]. 3rd ed. New York: John Wiley & Sons, 2000.

[27] ADACHI J, PEIRCE E, DESROCHES J. Computer simulation of hydraulic fractures[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(5): 739-757.

[28] BAO J Q, FATHI E, AMERI S. A unified finite element method for the simulation of hydraulic fracturing with and without fluid lag[J]. Engineering Fracture Mechanics, 2016, 162: 164-178.

[29] CARTER B J, DESROCHES J, INGRAFFEA A R, et al. Simulating fully 3D hydraulic fracturing[M]// ZAMAN M, BOOKER J, GIODA G. Modeling in geomechanics. New York: Wiley Publishers, 2000.

[30] DONTSOV E V, PEIRCE A. A Lagrangian approach to modelling proppant transport with tip screen-out in KGD hydraulic fractures[J]. Rock Mechanics and Rock Engineering, 2015, 48(6): 2541-2550.

（编辑 郭海莉）

Fracture propagation laws in staged hydraulic fracturing and their effects on fracture conductivities

BAO Jinqing1, 2, LIU He1, 2, ZHANG Guangming1, 2, JIN Juan1, 2, CHENG Wei1, 2, LIU Jiandong1, 2
(1. PetroChina Research Institute of Petroleum Exploration & Development, Beijing 100083, China; 2. Key Laboratory of Oil & Gas Production, China National Petroleum Corporation, Beijing 100083, China)

Completely taking into account the interferences between fractures as well as the friction effects on injection allocations, a fully coupled finite element method inherited from a verified one is proposed to discuss fracture propagation laws and analyze their impacts on fracture conductivities. Simulations show that although fractures have similar injection allocations that fluctuate around the allocation averaged by fractures, interferences between them lead to their different propagation rates and some fractures even stop propagating for a while. Shorter fractures generally have higher pressure and smaller pressure gradients than longer ones. The pressure differences between fractures result in long fractures having bottlenecking zones far away from the wellbore, and make them vulnerable to screen-out at the inlets and the bottlenecking zones. The effects of the propagation laws on fracture conductivities include: (1) the conductivities in short fractures are weakened by rapid proppant settlement in them; (2) long fractures may lost their conductivities due to screen-out near the wellbore; (3) the conductivities in long fractures decrease because of screen-out at the bottlenecking zones.

horizontal well; staged hydraulic fracturing; interference between fractures; fracture propagation; fracture conductivity

国家科技重大专项（2016ZX05023-001）

TE348

A

1000-0747(2017)02-0281-08

10.11698/PED.2017.02.14

包劲青（1977-），男，湖北大悟人，博士，主要从事水力压裂数值模拟方法方面的研究工作。地址：北京市海淀区学院路20号，中国石油勘探开发研究院采油工程研究所，邮政编码：100083。E-mail: JQBao@petrochina.com.cn

联系作者：刘合（1961-），男，黑龙江哈尔滨人，博士，中国石油勘探开发研究院教授级高级工程师，主要从事低渗透油气藏增产改造、机采系统提高系统效率、分层注水和井筒工程控制技术等方面的科研工作。地址：北京市海淀区学院路20号，中国石油勘探开发研究院院办，邮政编码：100083。E-mail: liuhe@petrochina.com.cn

2016-05-30

2017-01-24