MHD Flow and Heat Transfer of a Generalized Burgers’Fluid Due to an Exponential Accelerating Plate with Effects of the Second Order Slip and Viscous Dissipation∗
Yan Zhang(张艳), Hao-Jie Zhao(赵豪杰),and Yu Bai(白羽)
School of Science,Beijing University of Civil Engineering and Architecture,Beijing 100044,China
Beijing Key Laboratory of Functional Materials for Building Structure and Environment Remediation,Beijing University of Civil Engineering and Architecture,Beijing 100044,China
1 Introduction
In recent decades,the researches on the flow and heat transfer of viscoelastic fluid,which exhibit both elastic and viscous properties have received numerous attentions because its abundant applications in engineering,industrial and technology fields,such as extrusion of polymer fluids,continuous casting,exotic lubricants,foodstuffprocessing,wire and fiber coating,etc.[1−3]The fractional derivative has been found to be quite flexible in describing rheological characteristics of viscoelastic fluid.[4−6]Various fractional constitutive equations such as the generalized second grade fluid,[7−8]generalized Maxwell fluid,[9−10]generalized Oldroyd-B fluid,[11−12]and generalized Burgers’fluid[13−14]have been proposed.Compared with generalized second grade fluid,Maxwell fluid and Oldroyd-B fluid,the generalized Burgers’ fluid can better describe the performances of asphalt and asphalt concrete.Some recent works about the generalized Burgers’ fluid flow with fractional derivative method have been done.Khan et al.[15−17]obtained exact solutions for oscillating flow,accelerated flow and rotating flow of a fractional Burgers’fluid with the help of integral transforms.Ghada et al.[18]discussed the pressure gradient influence on the flow of generalized Burgers’ fluid.And a closed form solutions for the velocity and shear stress were derived in terms of Fox H-function by using the discrete Laplace transform.
Among the flows of viscoelastic fluids,the flow over an exponentially stretching sheet has many applications in industrial manufacturing processes such as production of polymer films or thin sheets.2D flow of viscoelastic fluid over an exponentially stretching sheet was carried out by Sanjayanand et al.[19]and Khan.[20]Sahoo et al.[21]discussed flow and heat transfer of a third grade fluid past an exponentially stretching sheet.Recently,Alhuthali et al.[22]and Hayat et al.[23]documented the 3D flow of viscoelastic fluid over an exponentially stretching surface.
MHD flow of a Newtonian fluid has been widely applied in energy generation and geophysical fluid dynamics.Recently,MHD flows of viscoelastic fluid have been also studied in detail.Hayat et al.[24]demonstrated MHD boundary layer flow of an upper-convected Maxwell fluid and obtained the analytical solution using homotopy analysis method(HAM).Khan et al.[25−26]discussed MHD flows of a generalized Oldroyd-B fluid and a generalized Burgers’ fluid.Furthermore,the related velocity distributions were calculated by means of Fourier transform and Laplace transform techniques for the fractional calculus.The results of the above study indicate that the magnetic field provides a force,which resists the flow since it is applied in the transverse direction.MHD flows under different situations have been dealt with in Refs.[27–30].
Beyond that,the viscoelastic fluids such as polymer solutions and suspensions,exhibit boundary slip,which is derived by a nonlinear and nonmonotonic relation between the slip velocity and the shear stress at the wall is a fascinating macroscopically physical phenomenon in hydrodynamics.In an interesting published literature,Thompson et al.[31]discovered that the velocity slip was connected with the slip length,the shear rate and the critical shear rate.Hayat et al.[32]and Shehawy et al.[33]investigated slip effects on peristaltic flows of a third order fluid and a non-Newtonian Maxwellian fluid.Recently,a new second order velocity slip model was proposed by Wu,[34]which showed the excellent agreement with the result of Fukui and Kaneko.[35]Subsequently,Zhu et al.,[36]Hayat et al.[37]and Mabood et al.[38]studied the effect of second order slip velocity on nano fluid respectively.The above investigations are mainly focused on the flow problem.
In fact,heat transfer of a viscoelastic fluid over a stretching sheet is often encountered in polymer processing engineering,steel fiber coating engineering,and foodstuff processing.Ezzat[39]investigated heat transfer of non-Newtonian fluid,in which a new formula of heat conduction equation with fractional derivative has been constructed in the context of generalized thermoelectric MHD theory.Subsequently,Zheng et al.[40]introduced the modified fractional Fourier’s law and Darcy’s law to discuss heat transfer of a generalized Maxwell fluid in a porous medium.Particularly,in analogy with the fractional momentum equation,Zheng et al.[41−43]obtained the fractional energy equation of a generalized Maxwell fluid.However,in view of the above researches,due to the high complexity of computation,no one has ever attempted to study the energy equation with the effect of viscous dissipation based on the fractional Burgers’ fluid constitutive relationship.
In the present work,we investigate MHD flow and heat transfer of a generalized Burgers’ fluid over an exponential accelerating plate with the effects of a second order velocity slip and viscous dissipation.The energy equation and momentum equation are coupled by the fractional Burgers’ fluid constitutive model.The finite difference method is an effective method to solve the fractional partial differential equations.[44−46]Numerical solutions for velocity,temperature and shear stress are obtained using the modified implicit finite difference method combined with the G1-algorithm.Moreover,the effects of relevant parameters on the velocity,temperature and shear stress fields are discussed graphically in detail.
2 Mathematical Formulation of the Problem
Unsteady flow and heat transfer of an incompressible generalized Burgers’ fluid due to an exponential accelerating plate is considered.It is assumed the fluid occupies the spacey>0.The forms of the velocity and shear stress fields are

whereuis the velocity and i is the unit vector in thexdirection,the initial condition S(y,0)=0.In addition,Sxx,Syy,Sxy,Syxare the components of shear stress and we haveSxx=Syy=0 andSxy=Syx.
According to Ref.[18],the fractional constitutive model of generalized Burgers’ fluid is given as follows

whereµ,λ1,andλ3are the dynamic viscosity,relaxation time and retardation time respectively,λ2is the material parameter,αandβare the fractional derivative parameters such that 0<α,β<1,,andare the Riemann–Liouville fractional differentiation operators,and the fractional derivative of orderp(m≤p<m+1,mis an integer)denotes as[4]
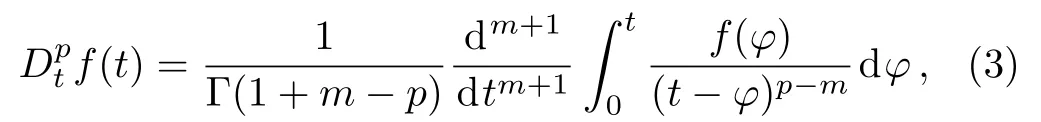
where Γ(·)is the Gamma function.
By ignoring the pressure gradient and heat source,the continuous,motion and energy equations are given by
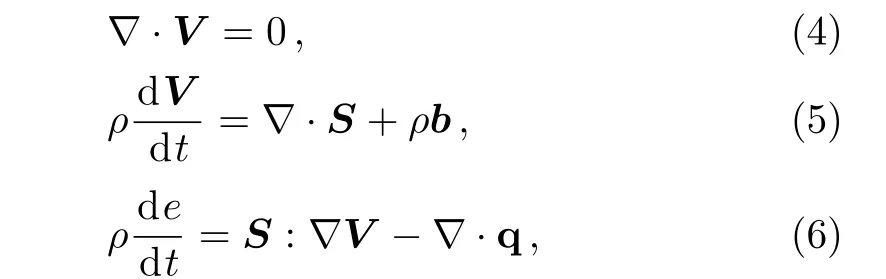
whereρ,b,e,and q denote the density of the fluid,the body force field,energy term,and heat flux respectively.
Consider a uniform magnetic fieldB0,which acts in the positivey-coordinate is introduced to the fluid.The magnetic body force can be written asσu(σis the electrical conductivity)when the assumption of low-magnetic Reynolds number.[47−48]Substituting Eq.(2)into Eq.(5),the governing equations can be written as
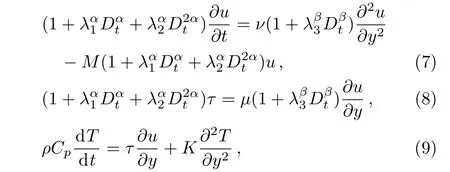
whereν=µ/ρis the kinematic viscosity,M=σ/ρis the magnetic parameter,Cpis the specific heat at constant pressure of the fluid,Tis the temperature,Kdenotes the thermal conductivity,τ=Sxyis the shear stress.
The corresponding initial and boundary conditions of motion and energy equations are


wherea,c,andu0are constants,T∞is the environment temperature,the velocity slip modelusliphas been given by Wu[34]and used also by Fang[49]and Rosca,[50]θ1(>0)is the first-order velocity slip parameter,θ2(<0)is the second-order velocity slip parameter.
Employ the non-dimensional quantities in Eqs.(7)–(15):

The dimensionless governing equations can be given as follows(for omitting the dimensionless mark “*” here)

whereη=/CpT∞is defined as boundary parameter,Mis the Hartmann number,Pr=CPµ/Kis the Prandtl number.
The initial and boundary conditions become
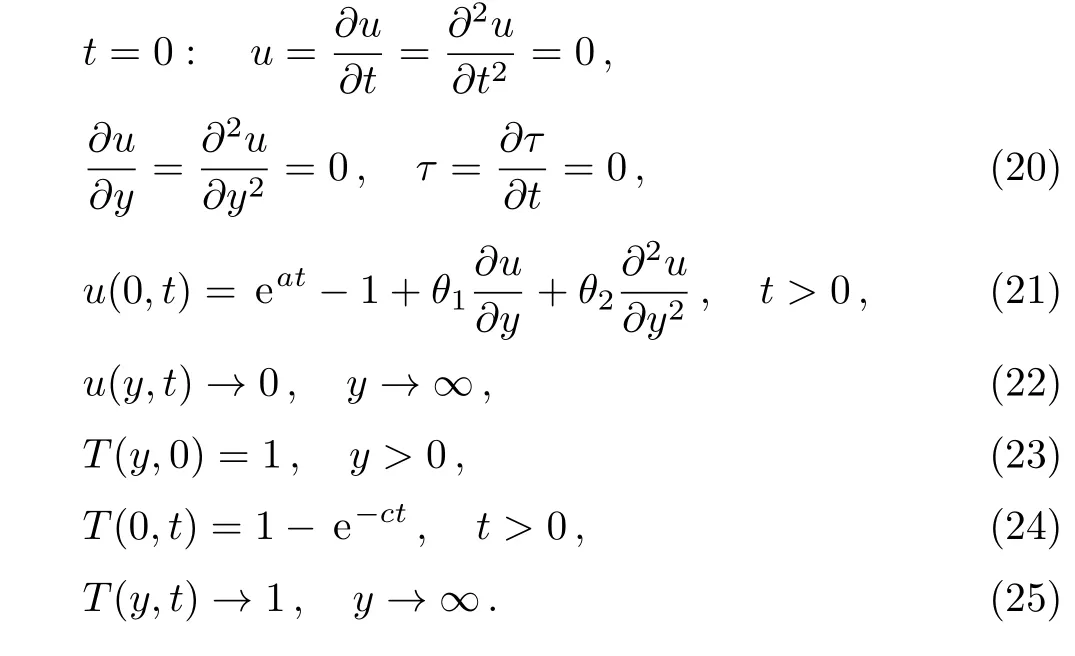
3 Numerical Calculations
Under the initial conditions,the Grünwald–Letnikov fractional derivative is equiva lent to the Riemann–Liouville fractional derivative.So we can obtain the numerical solutions with the G1 algorithm based on the standard Grünwald–Letnikov fractional derivative definition.
Definetn=nδ(n=0,1,...,N)andyi=ih(i=0,1,...,W),whereδ= Δt=t/Nis the time step,h=Δy=y/Wis the space step.Letandbe the numerical approximation tou(yi,tn)andT(yi,tn).The G1 algorithm is applied to discretize the fractional derivative of orderpas

Equation(26)is substituted into the governing equation(17),we can obtain
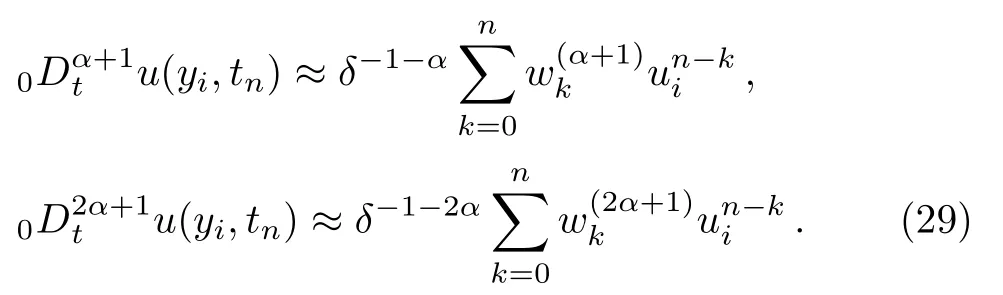
In the same way,we yield
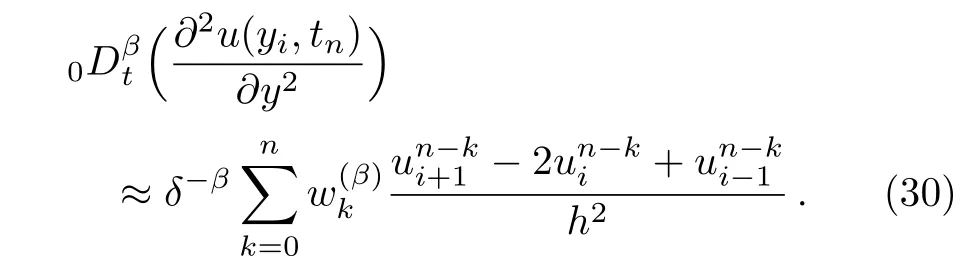
Similarly,the above method is dealt with Eqs.(17)–(19). Combining with the implicit finite difference method,we obtain the following iteration equations

Here,we construct an example with an analytic solution in order to show the convergence of the discrete schemes.Consider the following fractional equation:
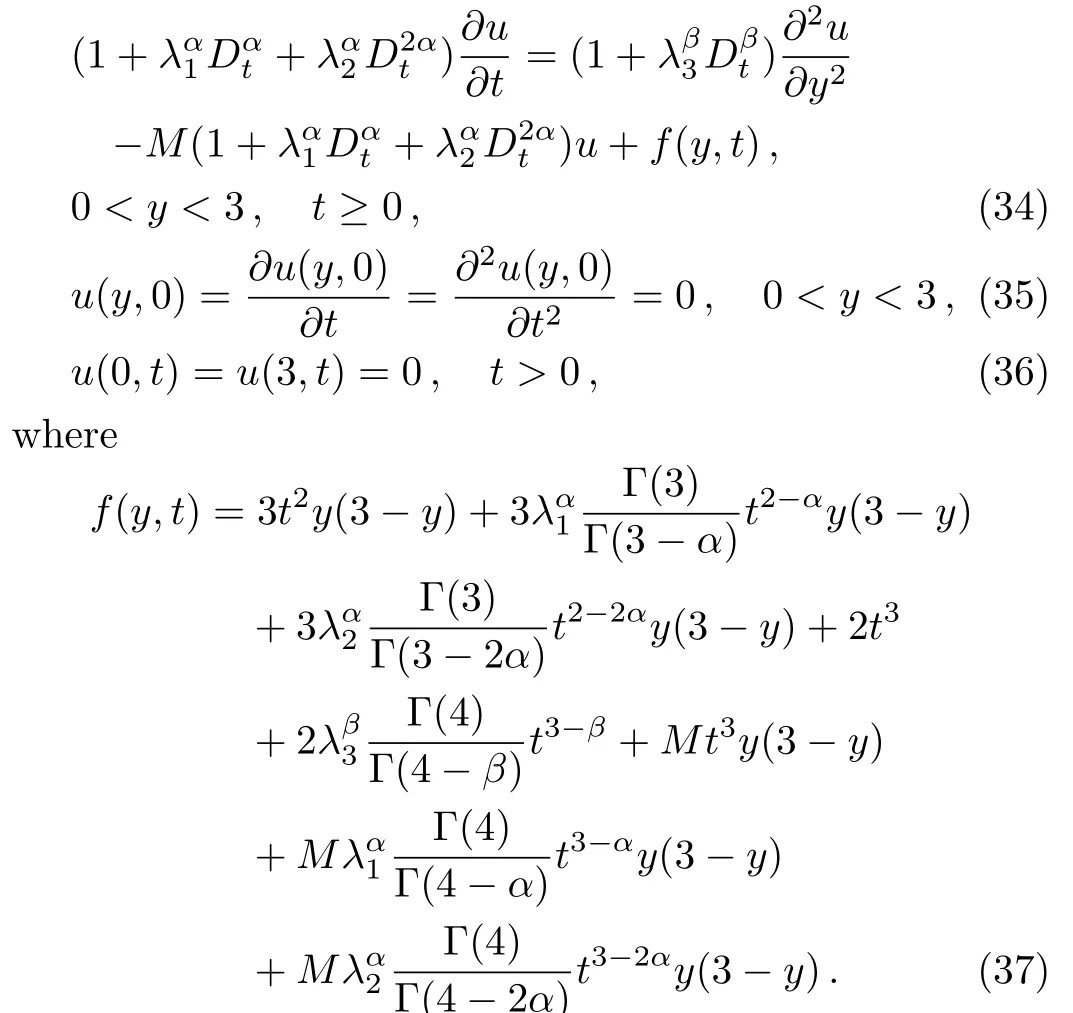
The analytical solution of Eq.(34)isu(y,t)=t3y(3−y).
The iteration equations of Eq.(34)obtained using numerical technique are as follow:

Figure 1 shows the comparison of the numerical solution with the analytical result.It can be seen that they are in good agreement each other.Simultaneously,let the maximum error MERR=shows the numerical errors between the numerical solutions and the analytical solution.It indicates that the error is reduced with the decrease of the step size.These results illustrate that the solution obtained by the finite difference scheme is convergent.

Table 1 Comparison of maximum errors(MERR).

Fig.1 Comparison of the example result of different method.
4 Results and Discussion
The numerical solutions of the velocity,temperature and shear stress are obtained by solving the numerical discrete equations(31)–(33).In order to study the characteristics of velocity,temperature and shear stress fields,the numerical results are plotted in Figs.2–12.

Fig.2 Velocity distribution for different α.
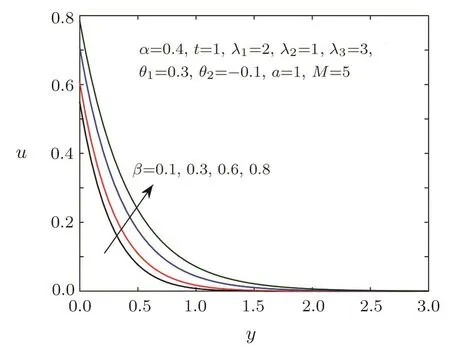
Fig.3 Velocity distribution for different β.
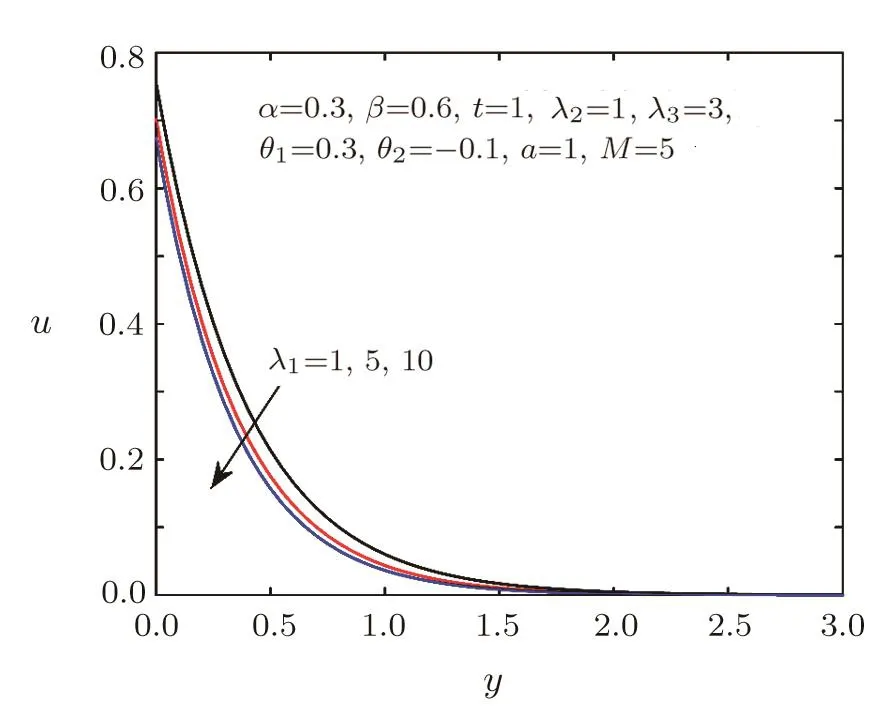
Fig.4 Velocity distribution for different λ1.
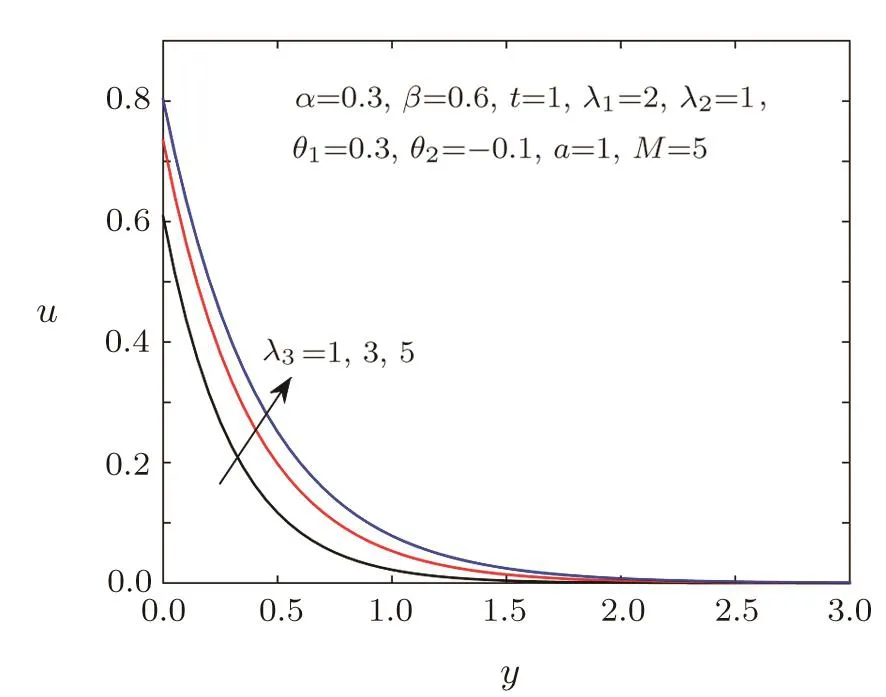
Fig.5 Velocity distribution for different λ3.
4.1 Effects on Velocity and Shear Stress Fields
Figures 2–3 show the impacts of the fractional parametersαandβon velocity field.We can find that the velocity distribution is strongly depended on the fractional parameters.Figure 2 tells us that the greaterαis,the lower velocity is,which implies that the thickness of the velocity boundary layer is thinner asαincreases.While Fig.3 displays thatβhas an opposite behavior.The effects of relaxation timeλ1and retardation timeλ3on the velocity field are presented in Figs.4–5,which can depict that viscoelastic fluid has the memory function.It is observed from Fig.4 that the velocity decreases with the increasing of relaxation timeλ1,which can be used to describe the stress relaxation characteristic of viscoelastic fluid.As shown in Fig.5,the velocity will be accelerated with the increase of retardation timeλ3,which can depict the delaying characteristic of viscoelastic fluid.Figure 6 provides the illustration for the influences of the first-order velocity slip parameterθ1and the second-order velocity slip parameterθ2on the velocity.An interesting physical phenomenon is discovered that when increasingθ1,the velocity pro file and the boundary layer thickness both decrease.However,the behavior ofθ2is opposite toθ1.Figures 7–8 show the velocity and shear stress pro files for different Hartmann numberM.The magnetic field provides a resistance named the Lorentz force causing a decrease in the velocity and shear stress.

Fig.6 Velocity distribution for different θ1and θ2.

Fig.7 Velocity distribution for different M.
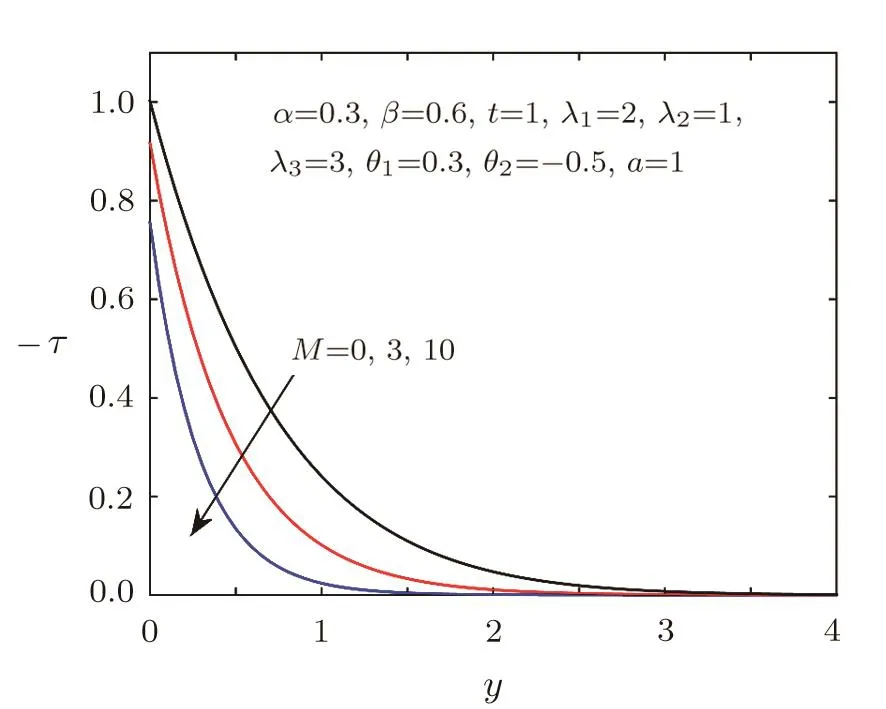
Fig.8 Shear stress distribution for different M.

Fig.9 Temperature distribution for different α.

Fig.10 Temperature distribution for different β.
4.2 Effects on Temperature Field
The effects of fractional parametersαandβ,Prandtl numberPrand boundary parameterηon the temperature are shown in Figs.9–12.From Figs.9–10,we can see that the impacts of fractional parametersαandβon the temperature are same as the velocity.Figure 11 illustrates that larger values ofPrlead to higher temperature and thinner boundary layer thicknesses.The effect ofηon the temperature is similar toPr,which is showed in Fig.12.It can be found that increasingηwill lead to the temperature rise,while has seldom effect to the boundary layer thickness.

Fig.11 Temperature distribution for different Prandtl number.
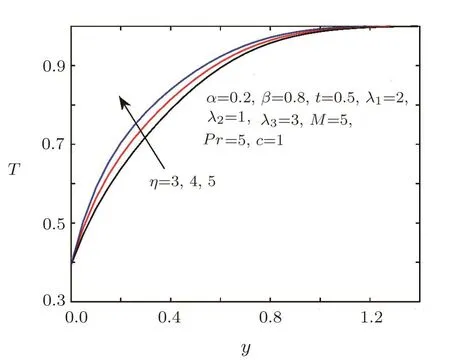
Fig.12 Temperature distribution for different η.
5 Conclusion
This paper provides a numerical analysis for MHD flow and heat transfer of an incompressible generalized Burgers’ fluid due to a slip accelerating plate.Numerical solutions are obtained by using the modified implicit finite difference method and the G1-algorithm.Validity of the proposed method is confirmed by the comparison of obtained numerical result and analytical result.The effects of fractional parameters,relaxation time,retardation time,slip parameters,Hartmann number,Prandtl number and boundary parameter on velocity,temperature and shear stress are analyzed.Obtained results indicate that the influences of the fractional parameterαon the velocity and temperature are opposite toβ.Meanwhile,the effects of relaxation time and retardation time on the velocity field are opposite each other.The influences of Prandtl number and boundary parameter on the temperature are similar.
Acknowledgments
The authors sincerely thank the editor and referees for their helpful comments and suggestions.
References
[1]L.C.Zheng,Y.Q.Liu,and X.X.Zhang,Math.Comput.Model.54(2011)780.
[2]˙I.Aslan,Commun.Theor.Phys.66(2016)315.
[3]B.Y.Shen,L.C.Zheng,and S.T.Chen,AIP Adv.5(2015)107133.
[4]I.Podlubny,Fractional Differential Equations,Academic Press,San Diego(1999).
[5]P.Roul,Commun.Theor.Phys.60(2013)269.
[6]L.C.Zheng,Y.Q.Liu,and X.X.Zhang,Nonlinear Anal.RWA 13(2012)513.
[7]M.Khan,S.Nadeem,T.Hayat,and A.M.Siddiqui,Math.Comput.Model.41(2005)629.
[8]M.Nazar,F.Corina,and A.Awan,Nonlinear Anal.RWA 11(2010)2207.
[9]C.Fetecau,M.Athar,and C.Fetecau,Comput.Math.Appl.57(2009)596.
[10]M.Jamil,A.Rauf,A.A.Zafar,and N.A.Khan,Comput.Math.Appl.62(2011)1013.
[11]M.Khan,S.H.Ali,and H.T.Qi,Nonlinear Anal.RWA 10(2009)980.
[12]L.C.Zheng,Z.L.Guo,and X.X.Zhang,Nonlinear Anal.RWA 12(2011)3499.
[13]C.F.Xue and J.X.Nie,Nonlinear Anal.RWA 9(2008)1628.
[14]S.H.Han,L.C.Zheng,and X.X.Zhang,J.Egypt.Math.Soc.24(2016)130.
[15]M.Khan,A.Anjum,C.Fetecau,and H.T.Qi,Math.Comput.Model.51(2010)682.
[16]M.Khan,S.Hyder Ali,and H.T.Qi,Nonlinear Anal.RWA 10(2009)2286.
[17]M.Khan,S.Hyder Ali,and H.T.Qi,Nonlinear Anal.RWA 10(2009)1775.
[18]H.I.Ghada and M.A.Ahmed,Int.J.Eng.Res.Appl.7(2014)19.
[19]E.Sanjayanand and S.K.Khan,Int.J.Therm.Sci.45(2006)819.
[20]S.K.Khan,Int.J.Appl.Mech.Eng.11(2006)321.
[21]B.Sahoo and S.Poncet,Int.J.Heat Mass Transf.54(2011)5010.
[22]M.S.Alhuthali,S.A.Shehzad,H.Malaikah,and T.Hayat,J.Petrol.Sci.Eng.119(2014)221.
[23]T.Hayat,I.Ullah,T.Muhammad,and A.Alsaedi,J.Mol.Liq.220(2016)1004.
[24]T.Hayat and M.Sajid,Int.J.Eng.Sci.45(2007)393.
[25]M.Khan,T.Hayat,and S.Asghar,Int.J.Eng.Sci.44(2006)333.
[26]M.Khan,R.Malik,and A.Anjum,Appl.Math.Mech.36(2015)211.
[27]M.M.Rashidi,Comput.Phys.Commun.180(2009)2210.
[28]M.M.Rashidi and E.Erfani,Comput.Fluids 40(2011)172.
[29]M.M.Rashidi,N.Vishnu Ganesh,A.K.Abdul Hakeem,and B.Ganga,J.Mol.Liq.198(2014)234.
[30]C.Fetecau,D.Vieru,C.Fetecau,and I.Pop,Eur.Phys.J.Plus 130(2015)6.
[31]P.A.Thompson and S.M.Troian,Nature(London)389(1997)360.
[32]T.Hayat,M.U.Qureshi,and N.Ali,Phys.Lett.A 372(2008)2653.
[33]E.F.El-Shehawy,N.T.El-Dabe,and I.M.El-Desoki,Acta Mech.186(2006)141.
[34]L.Wu,Appl.Phys.Lett.93(2008)253103.
[35]S.Fukui and R.Kaneko,ASME J.Tribol.112(1990)78.
[36]J.Zhu,D.Yang,L.C.Zheng,and X.X.Zhang,Appl.Math.Lett.52(2016)183.
[37]T.Hayat,M.Imtiaz,and A.Alsaedi,J.Magn.Magn.Mater.395(2015)294.
[38]F.Mabood and A.Mastroberardino,J.Taiwan Inst.Chem.Eng.57(2015)62.
[39]M.A.Ezzat,Phys.B 405(2010)4188.
[40]C.R.Li,L.C.Zheng,X.X.Zhang,and G.Chen,Comput.Fluids 125(2016)25.
[41]J.H.Zhao,L.C.Zheng,X.X.Zhang,and F.W.Liu,Int.J.Heat Mass Transf.97(2016)760.
[42]Z.Cao,J.H.Zhao,Z.Wang,F.W.Liu,and L.C.Zheng,J.Mol.Liq.222(2016)1121.
[43]J.H.Zhao,L.C.Zheng,X.X.Zhang,and F.W.Liu,Int.J.Heat Mass Transf.103(2016)203.
[44]M.L.Zheng,F.W.Liu,I.Turner,and V.Anh,SIAM J.Sci.Comput.37(2015)A701.
[45]F.H.Zeng,C.P.Li,F.W.Liu,and I.Turner,SIAM J.Sci.Comput.37(2015)A55.
[46]F.W.Liu,V.Anh,and I.Turner,J.Comput.Appl.Math.166(2004)209.
[47]S.Momani and Z.Odibat,Appl.Math.Comput.177(2006)488.
[48]T.Hayat,M.Khan,and M.Ayub,Appl.Math.Comput.151(2004)105.
[49]T.G.Fang,S.S.Yao,J.Zhang,and A.Aziz,Commun.Nonlinear Sci.Numer.Simulat.15(2010)1831.
[50]N.C.Rosca and I.Pop,Int.J.Heat Mass Transf.65(2013)102.
 Communications in Theoretical Physics2017年6期
Communications in Theoretical Physics2017年6期
- Communications in Theoretical Physics的其它文章
- A New Quantum Watermarking Based on Quantum Wavelet Transforms∗
- Effects of Variable Thermal Conductivity and Non-linear Thermal Radiation Past an Eyring Powell Nano fluid Flow with Chemical Reaction∗
- Analysis of Energy Eigenvalue in Complex Ginzburg–Landau Equation∗
- Role of Inclined Magnetic Field and Copper Nanoparticles on Peristaltic Flow of Nano fluid through Inclined Annulus:Application of the Clot Model
- MHD Stagnation Point Flow of Williamson Fluid over a Stretching Cylinder with Variable Thermal Conductivity and Homogeneous/Heterogeneous Reaction
- Rheological Analysis of CNT Suspended Nano fluid with Variable Viscosity:Numerical Solution
