Analysis of Energy Eigenvalue in Complex Ginzburg–Landau Equation∗
Ji-Hua Gao(高继华), Qi Xiao(肖骐),Ling-Ling Xie(谢玲玲),Xin-Xin Zhang(张昕昕),
and Hai-Tao Yang(杨海涛)‡
Key Laboratory of Special Functional Materials of Shenzhen,College of Materials,Shenzhen University,Shenzhen 518060,China
1 Introduction
In the recent decades,dynamics behavior of waves has been frequently studied in Reaction-Diffusion(RD)systems,and the great achievements have been made in this research field.Since the pioneering observation by Vanag and Epstein[1−2]discovering an inwardly spiral wave in a BZ-AOT experiment,the propagating direction of waves and the competition among different patterns have attracted great interests of the researchers.Brusch,Nicola,and Bär[3−5]made it clear that the regional criteria for outwardly propagating wave(OPW)and inwardly propagating wave(IPW)in the CGLE by analytical derivation.For the CGLE,the parameter domain where outwardly or inwardly propagating spiral waves emerges is well identi fied based on the definition of the phase velocity,Vph=ωk/kwhereωkandkrepresent the frequency and wave number respectively.In terms ofVph,it is positive for OPW and negative for IPW.Gong and Divid[3]found that IPW can occur only near the Hopf bifurcation in RD systems,and further evidence for their claim was provided by Brusch,Nicola,and Bär.[4−5]Before the discovery of an IPW,people considered that a necessary condition to produce an OPW is the frequency of wave is greater than bulk oscillation.Since IPWs were found in a RD experiment,Vanag and Epstein[1]concluded that a necessary condition to produce an IPW is that the frequency of wave is smaller than bulk oscillation.[6]Moreover,Shao et al.[7]selected CIMA reaction as their reaction system to investigate IPW.They found that in most cases inwardly propagating target waves dominate the system because they had a larger oscillation period(lower frequency)and suppressed inwardly propagating spiral waves with smaller periods.It is well known that the competitions between waves in a homogeneous oscillatory medium,as follows:[8−15]OPW against OPW,higher frequency dominates;OPW against IPW,OPW always dominates;IPW against IPW,lower frequency dominates.The above-mentioned rules were verified by researchers in the numerical or real experiments.From the viewpoint of nonlinear dynamics,they explained the accuracy of these rules as well.Our purpose of this work is to explore the mechanism of propagation and formation of waves,and competition of different patterns from the viewpoint of energy in the CGLE.
2 Model
We consider the CGLE,[16−18]which provides a universal description of oscillatory RDs close to the supercritical Hopf bifurcation that reads,
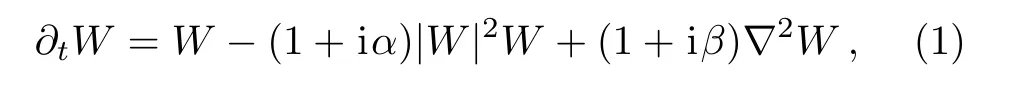
whereWis a complex spatiotemporal variable describing the amplitude of the pattern modulations.The real parametersαandβare the nonlinear frequency shift and dissipative coefficient,respectively.∇2=∂2/∂x2+∂2/∂y2is the two-dimensional Laplacian operator.
Equation(1)admits a stable spiral solution,which can be written in the polar coordinate as,

wherem=±1 is the topology charge of the single-arm spiral wave.ρ(r)andφ(r)are realfunctions satisfyingρ(r)∼φ′∼rasr→ 0;ρ(r)→φ′→kasr→ ∞.Here,the asymptotic frequencyωkand wave numberkare related via the nonlinear dispersion relationωk=ω0+(β−α)k2,whereω0=αis a bulk frequency.We use the Euler method to numerically integrate Eq.(1)in a rectangular coordinate system.No- flux conditions are imposed at the boundaries.The system consists ofL×Lgrid points.The space and time steps are Δx= Δy=0.5 and Δt=0.02,respectively.
3 Theoretical Derivation and Analysis
We use a phase-amplitude representation[19−20]in the CGLE.Substituting Eq.(2)into Eq.(1),we get,
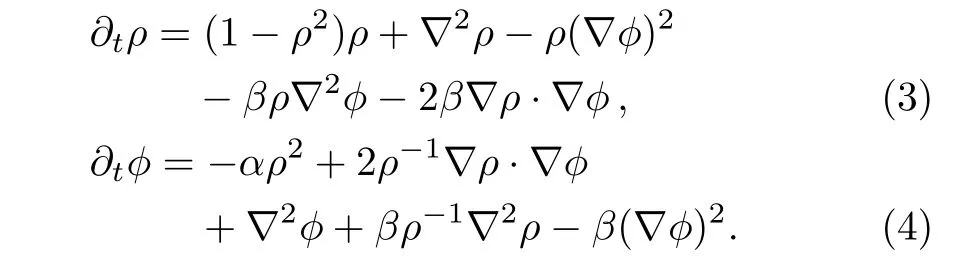
Considering in an area of non-defect turbulence,we assume thatρis stationary(∂tρ=0)and eliminatingρ2between Eq.(3)and Eq.(4)leads to,
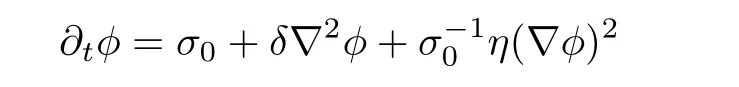

whereσ0= −α,δ=1+αβ,η=α(β−α).After applying Hopf–Cole transformationϕ=σ0η−1δ(lnQ− lnρ)to Eq.(5),the new variableQobeys the equation


Fig.1 Patterns of Re(W).System parameters are α =0.30,β = −1.34.
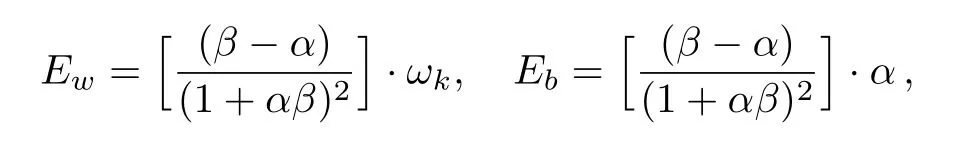
Analyzing Eq.(10),we find that the expression of energy eigenvalue consists of two sections for the CGLE system.We try to break Eq.(10)up and get corresponding to the energy eigenvalue of spiral wave and bulk oscillation. In Fig.1,we simulate the twodimensional system of Eq.(1)and obviously see two sections,spiral wave and bulk oscillation respectively,except from Fig.1(c).This is because the system is limited in 256×256 grid points.If we make the system enlarge to 512×512 grid points,you will see the two sections again att=160,as shown in Fig.1(f).Therefore,the numerical simulation result is consistent with the theoretical prediction.
In this section,we will make further analysis about the energy eigenvalue in the CGLE and acquire some interesting results,as follows:

Fig.2 Parameter space and patterns.(a)Parameter space(α,β)of the CGLE is separated by the curves ωk=0 and β − α =0 in four subdomains.(b)Pattern of IPW,system parameters are α = −0.3,β =1.4.We obtain ωk= −0.07 by Fast Fourier Transform(FFT),and Ew<0.(c)Pattern of OPW,system parameters are α = −0.1,β =1.4.We also obtain ωk=0.04 by FFT,and Ew > 0.(d)–(e)Corresponding space-time plots along the line y=128.The size of system is 256×256 grid points.
(a)We focus on the energy eigenvalue of spiral wave.For the CGLE,ktakes the same sign asβ−α.[5,21]Ew>0,for(β−α)ωk>0,namelyVph=ωk/k>0,the spiral wave propagates outwardly.Ew<0,for(β−α)ωk<0,namelyVph=ωk/k<0,the spiral wave propagates inwardly.In addition,Ew→∞,for 1+αβ→0,the spiral wave is unstable,which is corresponding to the curve of Benjamin–Feir Newell(BFN),as shown in Fig.2.This discovery associates the direction of energy transmission with wave propagation.Hence,we introduce a concept of general energy to predict the direction of wave propagation,and suppose that the direction is the same as energy transmission in the CGLE system.

Fig.3 Parameter space(α,β)of the CGLE is separated by the curves ωk=0, β − α =0 and α =0 in six subdomains,corresponding to the area of A1,B1,C1,A2,B2,C2.An OPW dominates in the area of A1,B1,A2,B2.An IPW dominates in the area of C1,C2.
(b)It is a necessary condition for generating a spiral wave that the energy eigenvalue of spiral wave is greater than bulk oscillation(Ew>Eb).Let us give more details as follows:
(i)We discuss the formation of OPW and obtainEw>0.Ifβ−α>0,thenωk>0.In view of the nonlinear dispersion relationωk=α+(β−α)k2,we getωk>α,thusEw>Eb.With this condition,we consider about two cases:(i)ωk>α>0,corresponding to the area of A1in Fig.3.It shows that this conclusion caters the previous findings[1,17]about the formation of OPW.(ii)ωk>0>α,corresponding to the area of B1in Fig.3.It is not easy to be judged which one is bigger between|ωk|and|α|.But we still know that the energy eigenvalue of spiral wave is greater than bulk oscillation,which is of our most interest.Ifβ−α<0,thenωk<0.According to the nonlinear dispersion relationωk=α+(β−α)k2,we getωk<α,andEw>Ebas well.Similarly,we consider two cases:(i)ωk<α<0,corresponding to the area of A2in Fig.3.At this time,|ωk|>|α|,this conclusion is also concord with the previous research results.(ii)ωk<0<α,corresponding to the area of B2in Fig.3.We cannot judge which one is bigger between|ωk|and|α|.Nevertheless,the energy eigenvalue of spiral wave is greater than bulk oscillation.
(ii)We consider the formation of IPW and obtainEw<0.Ifβ−α>0,thenωk<0.According to the nonlinear dispersion relationωk=α+(β−α)k2,we get 0>ωk>α,thusEw>Eb,corresponding to the area of C1in Fig.3.Hence,|ωk|<|α|,which is known that the condition for the formation of IPW.[1,10]Ifβ−α<0,thenωk>0.Based on the nonlinear dispersion relationωk=α+(β−α)k2,we get 0<ωk<α,thusEw>Eb,corresponding to the area of C2in Fig.3.This is also the condition for the formation of IPW.
(c)A wave with larger energy eigenvalue dominates when it competes with another wave with smaller energy eigenvalue in the CGLE system.Assuming that there are two waves exist in the CGLE system,are marked as“Wave-1” and “Wave-2” respectively,and “Wave-1” can defeat “Wave-2”.The frequency and energy eigenvalue of“Wave-1” isωk1andEw1;the frequency and energy eigenvalue of“Wave-2” isωk2andEw2.(i)OPW against OPW,higher frequency wins.Ifβ−α>0,thenωk1>ωk2>0,namelyEw1>Ew2>0.Ifβ−α<0,then|ωk1|>|ωk2|,ωk1<ωk2<0,namelyEw1>Ew2>0.(ii)OPW against IPW,OPW always wins.As we knowEw1>0,Ew2<0,thenEw1>Ew2.(iii)IPW against IPW,lower frequency wins.Ifβ−α>0,then|ωk1|<|ωk2|,ωk2<ωk1<0,namely 0>Ew1>Ew2.Ifβ−α<0,then 0< ωk1<ωk2,namely 0>Ew1>Ew2.

∂tW=(1 − iω)W−(1+iα)|W|2W+(1+iβ)∇2W,(11)whereωis the linear frequency parameter,and the nonlinear dispersion relationωk=ω0+(β−α)k2,whereω0=ω+αis a bulk frequency.In the CGLE,a circular heterogeneous area is introduced as follows:[17−21]

wherer=and(xc,yc)denotes the center of area with radiusr0.Our numerical simulation is under a premise condition for(β−α)Δω>0,which is a condition for creating an extended target wave.[17,19]For convenience and without losing the generality,we set|(β−α)/(1+αβ)2|=1 and obtainEw=|ωk|for OPW,Ew= −|ωk|for IPW.In Fig.4,we introduce a heterogeneous area with the center of area at(128,226)and radiusr0=16 in the CGLE system.As can be seen from Fig.4,an outward target wave and another inward spiral wave are generated(Eb<Es,Eb<Et),and the target wave ultimately dominates(Es<Et).
In the next section,we discuss the influence of local inhomogeneity with different sizes on the formation and propagation of wave.As shown in Fig.5,if we set the inhomogeneous area withr0=0,and an inwardly propagating spiral wave generates.We getEw= −|ωk|= −0.11 andEb=α=−0.20(β−α>0),thenEb<Ew<0.When we set the inhomogeneous area withr0=7∼20,a target wave generates in the system.Energy eigenvalue of target wave increases with the increasing size of inhomogeneous area and at the same time the direction of wave propagation changes from IPW to OPW.If we set the area occupying overall 256×256 system withr0=400,an outwardly propagating spiral wave generates.We getEw=|ωk|=0.15,Eb=ω+α=0.06(β−α >0),then 0<Eb<Ew.As we can be seen from Fig.5(a),energy eigenvalue of target wave is larger than inwardly propagating spiral wave forr0=0,but less than bulk oscillation forr0=400.

Fig.4 The cases of local inhomogeneity.Localized inhomogeneous area is introduced in CGLE,where the center of area at(128,226),and the radius of area is r0=16.Other parameters are α = −0.2,β =0.9,and Δω =0.26.Size of system is 256 × 256.(a)–(d)Patterns of Re(W)corresponding to t=40,t=80,t=160,t=400,respectively.(e)Corresponding space-time plot along the line y=128.(f)Energy eigenvalue of bulk oscillation,spiral wave and target wave is Eb=−0.20,Es=−0.10,and Et=0.04,respectively.
4 Discussion
Be widely known,waves represent an important means of transferring energy in the natural world.From our analysis results,we believe that the above discoveries are thought-provoking.We have discussed the mechanism for propagation and formation of waves,and competition among waves from the viewpoint of energy in the CGLE system.As the previous analysis and numerical simulations,the direction of wave propagation is the same as energy transmission.Energy eigenvalue of wave is positive,which shows that the wave propagates outwardly,namely its energy transfer from wave source to the outside.Vice versa for that the energy eigenvalue of wave is negative.We can see a target wave when a stone is thrown into the calm water of the lake.Its propagating direction is outward,and wave energy transfer from wave source to outside as well.Whether it is spiral or target wave,they both have sources which select their frequency and wavelength and control their surroundings.[5]Obviously,the energy of wave should be derived from wave source.Energy source of spiral wave is a point called topological defect,energy source of target wave is usually from an inhomogeneous area which is introduced,and energy source of bulk oscillation is itself.In addition,we bold speculate that wave energy is quantized,and its transmission is discrete.We attempt to introduce the concept of the minimal energy units(energy quantum)in the CGLE system that reads:Ew= ħ ·ωwhere ħ>0 is constant,andωrepresents frequency,ω=|ωk|for OPW;ω= −|ωk|for IPW.Therefore,a wave with larger energy quantum can generate and exist stably when it competes with another wave or bulk oscillation with smaller energy quantum in the CGLE system.

Fig.5 The influence of local inhomogeneity with different sizes.(a)Energy eigenvalue versus size of inhomogeneity.(b)–(e)Patterns of Re(W)for r0=0,r0=7,r0=16,r0=400,respectively,corresponding to the arrows in(a).(f)–(i)Corresponding space-time plots along the line y=128 of(b)–(e),where(f)and(g)show inwardly propagating wave(IPW),and(h)and(i)show outwardly propagating wave(OPW).Other parameters are α = −0.2,β =0.9,and Δω=0.26.The size of system is 256×256,and the center of inhomogeneous area is at(128,128).
5 Conclusions
In summary,our main work is to analyze and discuss the expression of energy eigenvalue in the CGLE system.We conclude that:(i)The energy eigenvalue in the CGLE system can be divided into two parts,corresponding to spiral wave and bulk oscillation.(ii)Positive energy eigenvalue represents the wave propagating outwardly,while negative energy eigenvalue represents the wave propagating inwardly.(iii)A wave with larger energy eigenvalue can generate and exist stably when it competes with another wave or bulk oscillation with smaller energy eigenvalue in the CGLE system.
Our work try to build a relationship between wave propagation and energy transmission.The introduced energy eigenvalue provides a new insight in understanding the behavior of nonlinear traveling waves and competition among waves.On one hand,we hope that this theory can apply to an experimental study with realistic back-ground,and account for dynamics behaviors of wave for wider fields.On the other hand,we hope that the energy eigenvalue,which is commonly used in the microscopic study and quantum mechanics and,to our knowledge,is firstly defined in the CGLE system to investigate the pattern propagations and competitions,provides a new road for a better understanding of our world.
References
[1]V.K.Vanag and I.R.Epstein,Science 294(2001)835.
[2]V.K.Vanag and I.R.Epstein,Phys.Rev.Lett.88(2002)088303.
[3]Y.Gong and D.J.Christini,Phys.Rev.Lett.90(2003)088302.
[4]L.Brusch,E.M.Nicola,and M.Bär,Phys.Rev.Lett.92(2004)089801.
[5]E.M.Nicola,L.Brusch,and M.Bär,J.Phys.Chem.B 108(2004)14733.
[6]R.Zhang,L.Yang,A.M.Zhabotinsky,and I.R.Epstein,Phys.Rev.E 76(2007)016201.
[7]X.Shao,Y.Wu,and J.Zhang,Phys.Rev.Lett.100(2008)198304.
[8]F.Xie and J.N.Weiss,Phys.Rev.E 75(2007)016107.
[9]X.Cui,X.Huang,and G.Hu,Phys.Rev.E 78(2008)026202.
[10]Z.Cao,H.Zhang,and G.Hu,Eur.Phys.Lett.79(2007)34002.
[11]M.Hendrey,K.Nam,P.Guzdar,and E.Ott,Phys.Rev.E 62(2000)7627.
[12]X.Cui,Y.Dong,and X.Huang,Commun.Theor.Phys.63(2015)359.
[13]B.Li,H.Ying,J.Yang,and X.Gao,Phys.Lett.A 374(2010)3752.
[14]X.J.Yuan,H.L.Wang,and Q.Ouyang,Phys.Rev.Lett.106(2011)188303.
[15]X.Cui,X.Huang,and G.Hu,Sci.Rep.6(2016)25177.
[16]F.Xie,D.Xie,and J.N.Weiss,Phys.Rev.E 74(2006)026107.
[17]Y.Kuramoto,Chemical Oscillations,Waves,and Turbulence,Springer-Verlag,Berlin(1984)
[18]I.S.Aranson and L.Kramer,Rev.Mod.Phys.74(2002)99.
[19]P.S.Hagan,SIAM J.Appl.Math.42(1982)762.
[20]M.Stich and A.S.Mikhailov,Physica D 215(2006)38.
[21]T.Li and B.Li,Chaos 23(2013)033130.
 Communications in Theoretical Physics2017年6期
Communications in Theoretical Physics2017年6期
- Communications in Theoretical Physics的其它文章
- A New Quantum Watermarking Based on Quantum Wavelet Transforms∗
- Effects of Variable Thermal Conductivity and Non-linear Thermal Radiation Past an Eyring Powell Nano fluid Flow with Chemical Reaction∗
- Role of Inclined Magnetic Field and Copper Nanoparticles on Peristaltic Flow of Nano fluid through Inclined Annulus:Application of the Clot Model
- MHD Flow and Heat Transfer of a Generalized Burgers’Fluid Due to an Exponential Accelerating Plate with Effects of the Second Order Slip and Viscous Dissipation∗
- MHD Stagnation Point Flow of Williamson Fluid over a Stretching Cylinder with Variable Thermal Conductivity and Homogeneous/Heterogeneous Reaction
- Rheological Analysis of CNT Suspended Nano fluid with Variable Viscosity:Numerical Solution
