Effects of Variable Thermal Conductivity and Non-linear Thermal Radiation Past an Eyring Powell Nano fluid Flow with Chemical Reaction∗

M.Ramzan,M.Bilal,Shamsa Kanwal,and Jae Dong Chung

1Department of Computer Science,Bahria University,Islamabad Campus,Islamabad 44000,Pakistan

2Department of Mathematics,Faculty of Computing,Capital University of Science and Technology,Islamabad 44000,Pakistan

3Department of Mathematical Sciences,Fatima Jinnah Women University,Rawalpindi,Pakistan

4Department of Mechanical Engineering,Sejong University,Seoul 143-747,Korea

It is generally an accepted fact that non-Newtonian lfuids are more industry oriented as compared to Newtonian fluids.Glue,coal water,custard,ketchup,inks,cosmetics,toothpaste and jellies are some examples of non-Newtonian fluids.Unlike Newtonian fluids,no single relation can be predicted for non-Newtonian fluids as each non-Newtonian fluid possesses varying properties of viscosity and elasticity,which makes the mathematical modeling of these fluids more complicated as compared to Newtonian fluids.Many researchers are involved in exploring the new dimensions in this area.[1−5]Each non-Newtonian fluid model holds different features to exhibit a physical phenomenon.Eyring Powell fluid model[6−8]is one such model that can be extracted from kinetic theory of gases instead of Power law model.However,at low and high sheer rates,it exhibits the Newtonian behavior rather than pseudo-plastic systems’behavior.At different polymer concentrations,Eyring Powell model is considered to be more precise and reliable in estimating the fluid time scale.[9]

In the present era of industrial revolution,Choi’s pioneering work[10]in nano fluids characterized by their ability to upsurge the thermal conductivity of base liquid,has opened the gates for followers to work in new dimensions.Choi found that heat transfer rate can be doubled by adding a small amount of nano particles.The novel characteristics of thermophoresis and Brownian motion of

1 Introduction

such fluids also make them potentially practical.Applications of nano fluids include cooling of micro chips,nanodrug delivery,and cancer therapy.Many researchers are exploring new dimensions and adding valuable contributions toward nano fluids.Some of these include exploration by Sohail and Saleem[11]that explores a time dependent f l ow on a rotating cone of Eyring Powell nano fluid under the impact of mixed convection.Waqar et al.[12]studied three-dimensional heat generation/absorption flow of an Oldroyd-B nano fluid.Khan et al.[13]focused 3D nano fluid f l ow in lateral directions over a nonlinearly stretched sheet.Jalilpour et al.[14]focused MHD stagnation point nano fluid flow in the presence of prescribed heat flux and heat generation/absorption past a porous stretching sheet.In recent literature,various dimensions have been explored in the presence of nano fluids.[15−20]

In general,four heating processes are available in the literature namely(i)prescribed surface heat flux,(ii)prescribed wall temperature,(iii)Newtonian heating,and(iv)conjugate/convective boundary conditions.In today’s modern world,demand for compact and light weight devices for technological and engineering machinery urge researchers to explore more avenues in heat transfer equipment with enhanced efficiency.Due to this increasing demand of small and light weight units,researchers have been focusing on effects on interface between axial wall conduction and thermal boundary layers in fluids that directly influence the heat exchange performances.Convec-tive boundary condition is the generalized concept of prescribed surface temperature and prescribed heat flux conditions.Convective boundary condition is derived from the amalgamation of Newton’s law of cooling and Fourier’s law of heat conduction.It can be reduced to both prescribed surface temperature and heat flux conditions by making Biot number tends to infinity and zero respectively.Many researchers are exploring new mathematical models involving convective heat condition.To mention few amongst these,the study by Ibrahim[21]who examined the magnetohydrodynamic flow of nano fluid near the stagnation point under the influence of convective boundary condition.Ibanez[22]studied MHD flow past a channel with permeable walls in attendance of convective and hydrodynamic slip boundary conditions.Mustafa et al.[23]addressed the radiative Maxwell fluid flow with impact of convective condition.Recently,a variety of alluring problems highlighting effects of convective boundary condition are discussed,see Refs.[24–27].

In above referred studies,none of these have disused combined effects of non-linear thermal radiation and variable thermal conductivity with amalgamation of chemical reaction.This has motivated us to study the problem of Eyring Powell nano fluid flow in presence of heat and mass convective boundary conditions past a continuously moving surface.No such study has been carried out till now in the literature as far as our knowledge is concerned.Series solutions have been obtained using famed Homotopy Analysis method(HAM).[28−31]Partial differential equations with high nonlinearity are changed into nonlinear ordinary differential equations using appropriate transformation.Graphs of Skin friction coefficient,local Nusselt and Sherwood numbers with mandatory conversation versus various parameters are also added.

2 Mathematical Formulation

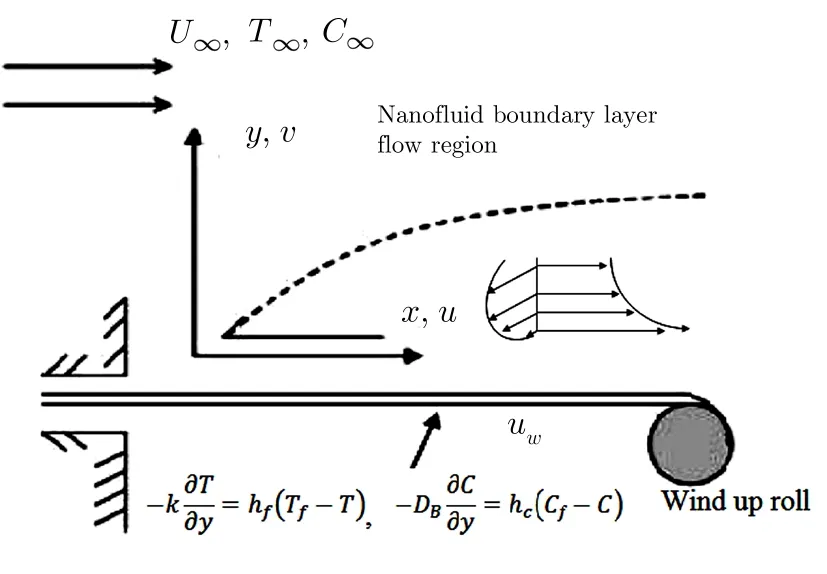
Fig.1 Flow diagram.

We assume 2D steady flow of an incompressible Eyring Powell nano fluid past a surface moving with constant velocityuw.Both constant velocityuwand uniform free stream velocityu∞have the same direction.Wall temperatureTwand free stream temperatureT∞are constant with the assumptionTw＞T∞in attendance of convective heat and mass boundary conditions(See Fig.1).

The Cauchy stress tensor in an Eyring–Powell model[6]is governed by the relation:

whereµandβ,care dynamic viscosity and material fluid constants of Eyring Powell fluid model.Considering

the continuity,momentum,energy and concentration equations yield

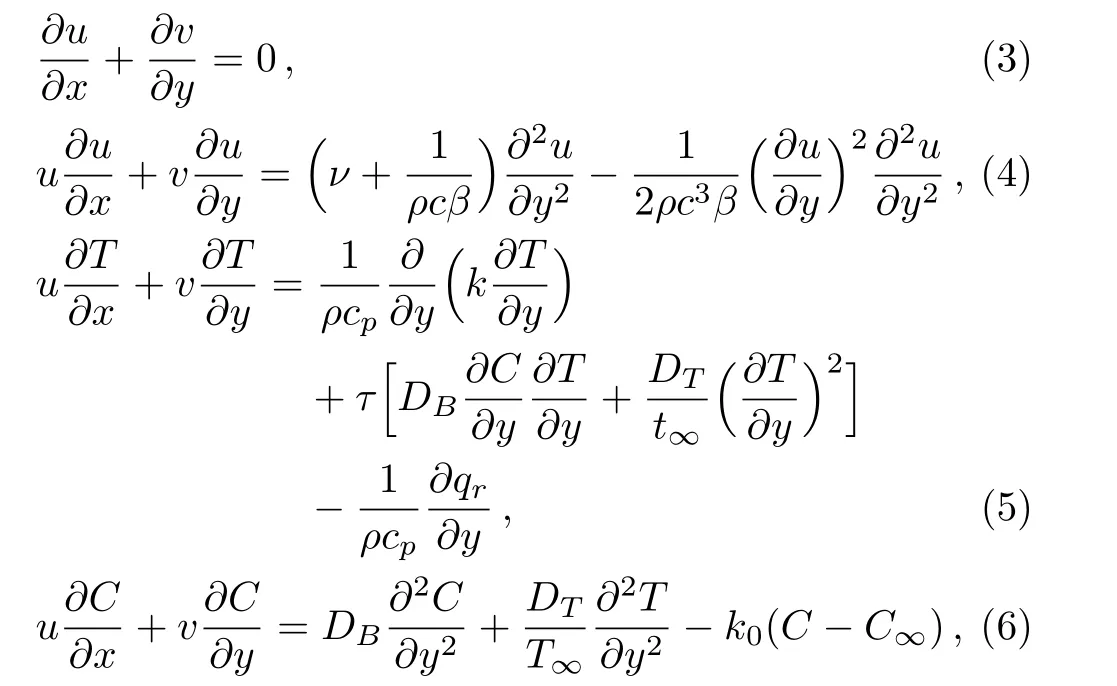
with the boundary conditions

whereuandvdenote the velocity components in thexandydirections,respectively.ν=µ/ρ,ρ,τ,DB,C,T,Tf,T∞,Cf,andC∞are the kinematic viscosity,density,ratio of effective heat capacity of nanoparticles to the heat capacity of the fluid,Brownian motion coefficient,concentration of species, fluid temperature,the convective fluid temperature below the moving sheet,ambient temperature,concentration below the moving sheet and concentration far away from the sheet,respectively.k,cp,DT,hfandhcare the thermal conductivity,specific heat at constant pressure,thermophoretic diffusion coefficient,convective heat transfer coefficient and convective mass transfer coefficient respectively.Using the transformations

Considering variable thermal conductivityk=ka(1+αθ(η))withα=(k−ka)/kaas defined in Ref.[32].The nonlinear radiative heat fluxqrvia Rosseland’s approximation is

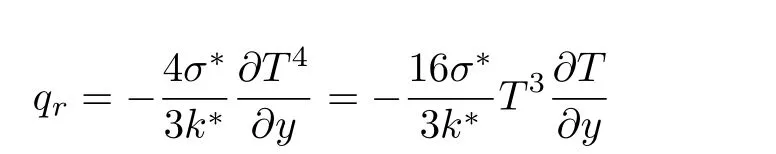
withσ∗andk∗are Stefan–Boltzmann constant and the mean absorption coefficient respectively.Equation(3)is identically satis fied while Eqs.(4)to(7)are reduced to

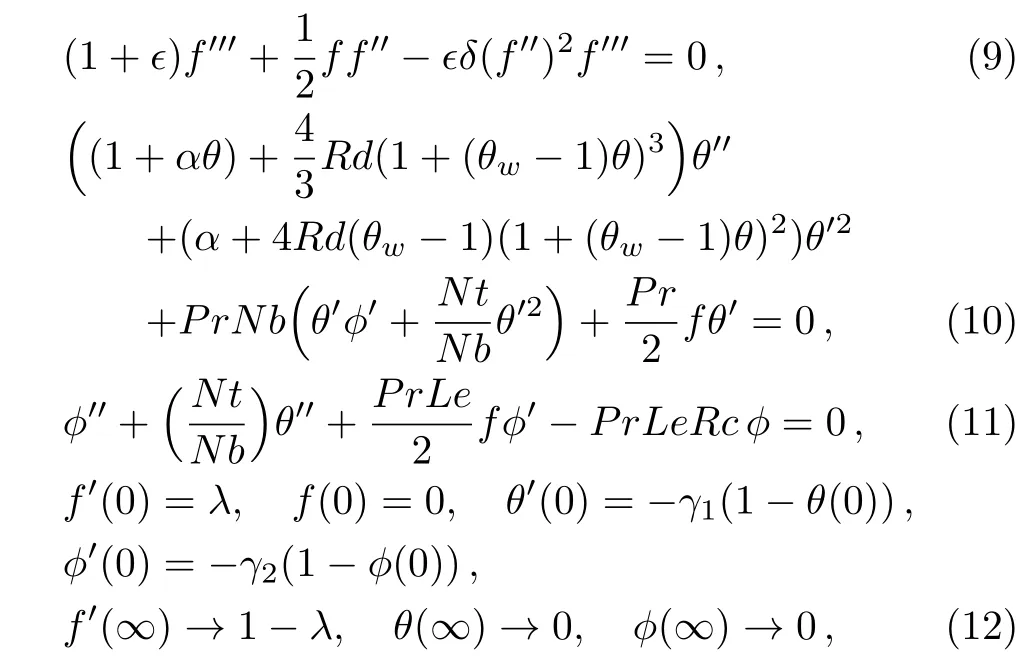
whereλ,ϵandδ,θw,α,Rd,Pr,Nt,Rc,Le,Nb,γ1andγ2are constant parameter, fluid parameters,the temperature ratio parameter,thermal conductivity parameter,thermal radiation parameter,Prandtl number,thermo phores is parameter,Chemical reaction parameter,Lewis number,Brownian motion parameter,heat transfer and mass transfer Biot numbers respectively.The values of these parameters are given below:

The caseλ=0 relates to the flow over an immobile surface because of free stream velocity.However,λ=1 points out the moving plate in the fluid.The flow of fluid and plate moving in the same direction is represented by the case 0＜λ＜1.Here,we consider the caseλ≤1.

The skin friction coefficient Cf,local Nusselt numberNux,and Sherwood numberShxcan be written as:

In non-dimensional forms Skin friction,local Nusselt and Sherwood numbers are

withRex=Ux/νis the local Reynolds number.

3 Homotopic Solutions

Liao[36]suggested Homotopy Analysis method in 1992 for the construction of series solutions of differential equations with high nonlinearity.This method has advantages over the contemporary methods because of the following reasons:

(i) This method is independent of selection of large or small parameters.

(ii) Convergence of series solution in this method is guaranteed.

(iii) Ample choice for the selection of base functions and linear operatos is available in this method.

Initial guess estimates(f0,θ0,ϕ0)required for series solutions in Homotopy analysis method are defined as:

with auxiliary linear operators(Lf,Lθ,Lϕ)given by

with ensuing characteristics

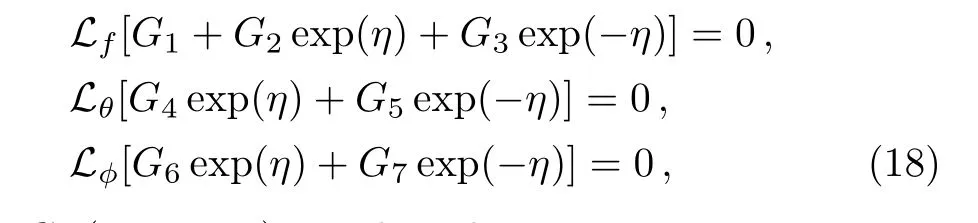
whereGi(i=1−7)are the arbitrary constants.

3.1 Zeroth-Order Problem

The problem at zeroth order is assembled as

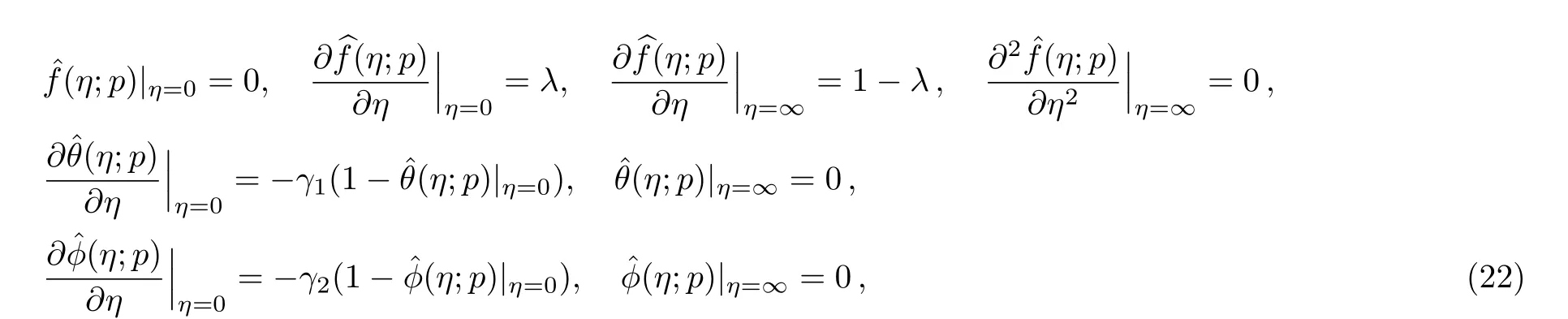
with nonlinear operators Nf,Nθ,and Nϕare given by

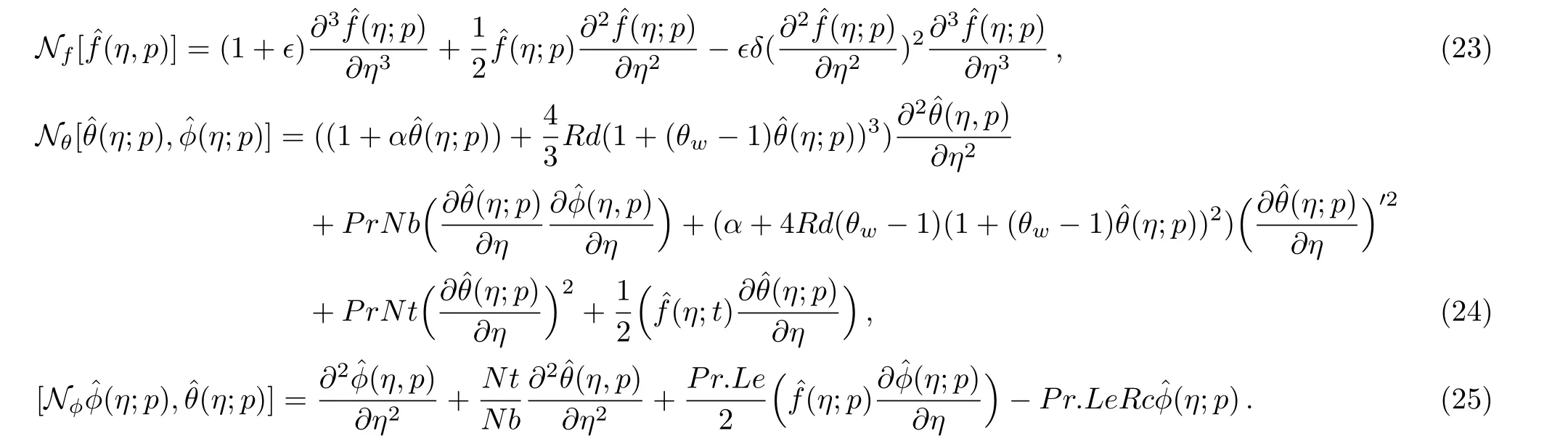
Here,non-zero auxiliary parameters are ħf, ħθ,and ħϕ,withpis an embedding parameter such thatp ϵ[0,1].Having valuesp=0 andp=1,we get

If we changepfrom 0 to 1,the values of the functionsf(η,p),θ(η,p)andϕ(η,p)will fluctuate from initial guessesf0(η),θ0(η),ϕ0(η)to the final solutionsf(η),θ(η),ϕ(η)respectively.With the help of Taylor’s series,Eqs.(26)to(28)take the form

The value of auxiliary parameters ħf,ħθ,and ħϕare selected in such a manner that the series(29)–(31)converge atp=1,i.e.,

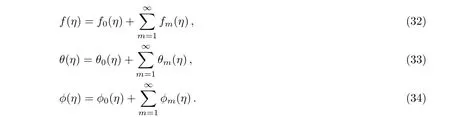
3.2 m-th Order Deformation Problems

Them-th order deformation problem is obtained by taking successive derivativesmtimes of Eqs.(19)to(22)w.r.t p,and division bym!and at the end usingp=0,we get

The general solutions in the form of special solutions

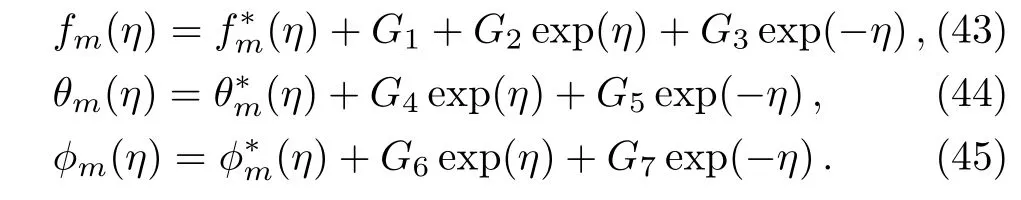
Here,constantsGi(i=1–7)through boundary conditions(38)are appended as

The problems comprise of Eqs.(35)–(41)are solved by employing Mathematica software,assumingm=1,2,3,...

4 Convergence Analysis

Series solution requires convergence region.Auxiliary parameters ħf,ħθ,and ħϕplay a key role in achieving this goal.To find this region,Fig.2 is drawn to show ħ-curves whenϵ=0.4,δ=0.4,γ1=γ2=0.1,λ=0.4,Pr=1,Nt=0.8,Nb=0.2,Rd=0.4,Rc=0.3,θw=1.3,α=0.2,andLe=1.0.The endurable ranges of the auxiliary parameters ħf,ħθand ħϕare −1.4 ≤ ħf≤ −0.3,−1.4≤ ħθ≤ −0.3,and−1.4≤ ħϕ≤ −0.3 respectively.Table 1 shows the convergence of HAM solution.It is observed that 29thorder of approximation is good enough for convergent series solution.The values obtained in the Table are consistent with the tolerable ranges in the graph.

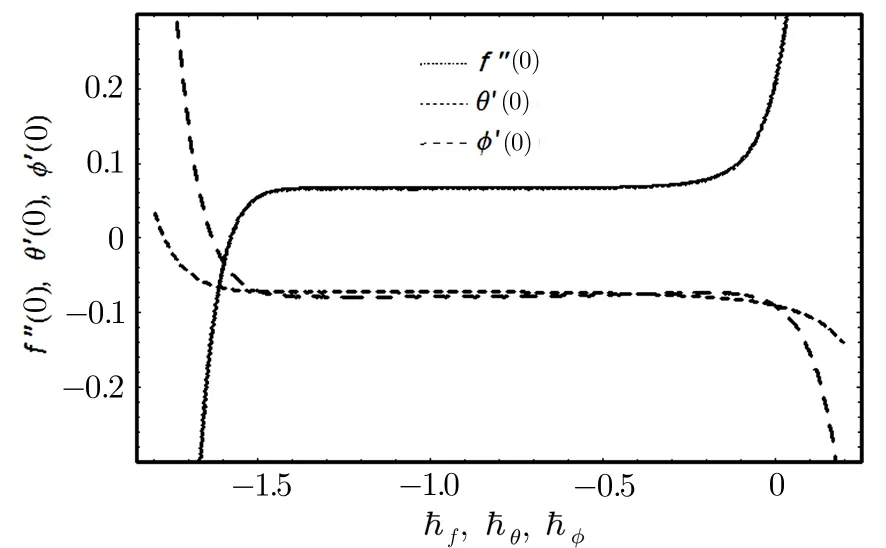
Fig.2 ħ-curves of f,θ,and ϕ.

Table 1 Series solutions’convergence for varied order of approximations when ϵ=0.4,δ=0.4,λ =0.4,Nb=0.2,Le=1.0, γ1= γ2=0.1,Nt=0.8,Pr=1.0,Rd=0.4,Rc=0.3,θw=1.3,α =0.2,ħf= −0.7, ħθ= −0.7,and ħϕ= −0.7.

5 Results and Discussion

This segment emphasis on the discussion of graphical illustrations of different emerging parameters on all dimensionless distributions.

Fig.3 Impact of ϵ on f′(η)when λ =1.0.

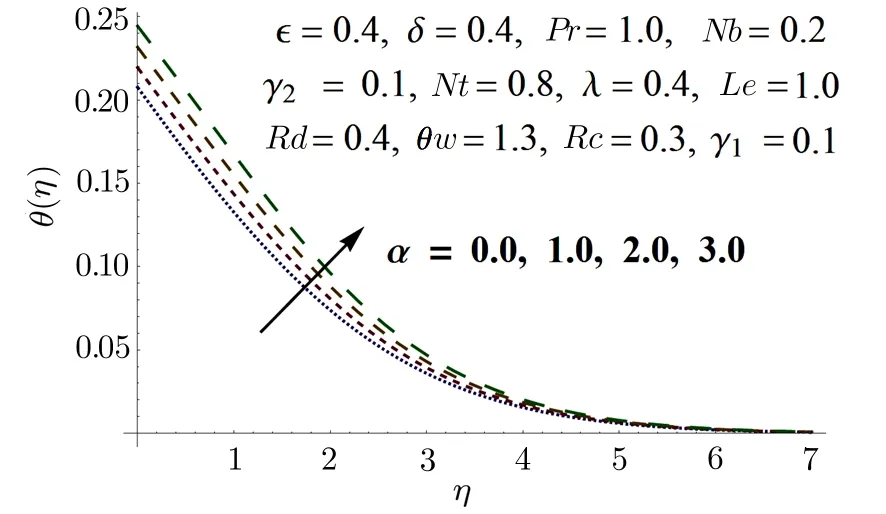
Fig.5 Impact of α on θ(η).

Fig.7 Impact of γ2on ϕ(η).

Fig.9 Impact of Nb on θ(η).

Fig.4 Impact of ϵ on f′(η)when λ =0.4.

Fig.6 Impact of γ1on θ(η).

Fig.8 Impact of Pr on θ(η).

Fig.10 Impact of Nt on θ(η).

Figures 3 and 4 illustrate the impact of fluid parameterϵon the velocity field for two separate values ofλ.It is clear from Fig.3 that velocity and momentum boundary layer thickness escalate with growing values ofϵ,whenλ=1(Sakiadis flow).[32]However,the velocity decreases with increase in value ofϵforλ=0.4.The impact of variable thermal conductivity parameterαon temperature field is displayed in Fig.5.It is clear from the figure that temperature distribution shows increasing tendency when value ofαis increased.This is because of an accepted fact that liquids with higher thermal conductivity possesses higher temperature.The effects of Biot numbersγ1andγ2with(0＜γ1,γ2＜1),on temperature and concentration distributions have been portrayed in Figs.6 and 7.Here,it is observed that temperature increases rapidly forγ1=0.1,0.2 but a low increment is witnessed forγ1=0.3,0.4.It means that for smaller values of heat transfer Biot numbersγ1,temperature profile increases rapidly but for larger values ofγ1,the temperature pro file increases slowly.Similar behavior in case of mass transfer Biot numberγ2is witnessed in Fig.7.Figure 8 is drawn to illustrate the consequence of Prandtl numberPron temperature distribution.From the definition of Prandtl numberPr=µct/k=v/α,we see that for higher Prandtl number,thermal diffusivity must have a smaller value.So,a gradual upsurge in Prandtl number results in reduction in boundary layer thickness and temperature pro file.From Fig.9,it is obvious that an increase in Brownian motion parameterNb,enhances collision of particles and thus boosts the temperature pro file and its related boundary layer thickness.Effect of thermo phoresis parameterNton temperature field is shown in Fig.10.It is observed that an upsurge in values ofNtleads to an increase in the temperature pro file and its allied boundary layer thickness.

Fig.11 Impact of Rd on θ(η).

Fig.13 Impact of ϵ and δ on CfRe−1/2x .

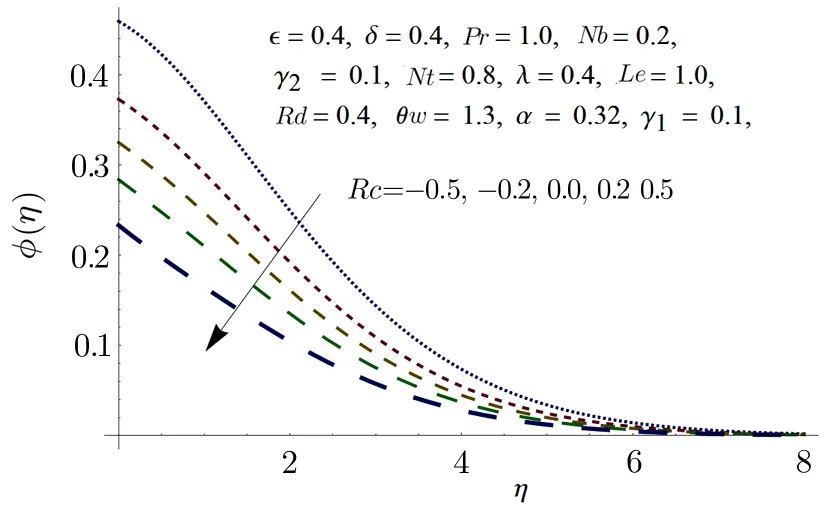
Fig.12 Impact of Rc on ϕ(η).

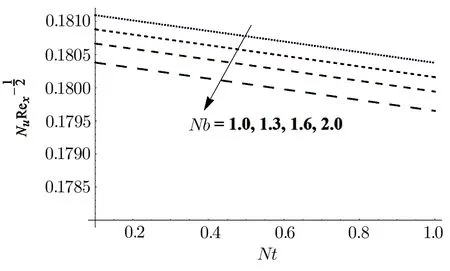
Fig.14 Impact of Nb and Nt on NuxRe−1/2x .

Fig.15 Impact of Le and Pr on ShxRe−1/2x .

From Fig.11,it is evident that temperature pro file is growing function of non-linear thermal radiation parameterRd.Actually,increasing values ofRdboosts the thermal boundary thickness.This is due to the fact that increase in thermal radiation parameter results in decrease in mean absorption coefficient,which eventually upsurges the divergence of the radiative heat flux.That is why the fluid’s temperature increases due to increase in rate of radiative heat transfer.Figure 12 is portrayed to show the effects of chemical reaction parameterRcvarying from non-destructive(Rc＜0)to destructive(Rc＞0)on concentration distribution.The solute concentration diminishes because of destructive chemical reaction;this eventually decreases the solutal boundary layer thickness by a small amount and the negative wall slope of the concentration distribution.An opposing impact is observed in case of non-destructive chemical reaction.

Figure 13 depicts the effects of fluid parametersδandϵof Skin friction coefficient.Observations show that Skin friction coefficient escalates for higher values ofϵ.However,opposite behavior is witnessed in case ofδ.The influence of thermophoresis parameterNtand Brownian motion parameterNbon Nusselt number is displayed in Fig.14.For growing values of bothNbandNt,decrease in Nusselt number is perceived.For growing values of Lewis numberLeand Prandtl numberPr,Sherwood number shows an increasing tendency.This effect is shown in Fig.15.

Table 2 Comparison of values for −θ′(0)with those of Hayat et al.[35]and Aziz[36]for different values γ1= γ2in absence of nano fluid and ϵ=0.

Table 2 depicts the comparison of existing series solutions with Hayat et al.[35]and Aziz[36]in limiting case.An outstanding agreement is found amongst the three solutions.

6 Final Remarks

Effects of convective boundary conditions on time independent boundary layer Eyring Powell nano fluid flow past a constantly moving surface in attendance of free stream velocity is discussed.Effects of non linear thermal radiation,chemical reaction,and variable thermal conductivity are also taken into account.Series solution for the said problem is obtained using Homotopy Analysis method(HAM).The prominent outcomes of this problem are:

•Temperature field is declining function ofPr.

•Temperature distribution is growing function ofNbandNt.

•Chemical reaction parameterRcis a dwindling function of concentration pro file.

•Temperature distribution shows increasing tendency when values of thermal conductivity parameterαis increased.

•Temperature distribution is growing function ofRd.

•Values of Sherwood number are increased when the values ofLeandPrare larger.

Competing Interests:

The authors declare no competing interests.

References

[1]M.Ramzan and M.Bilal,Journal of Molecular Liquids 215(2016)212.

[2]T.Hayat,M.Awais,and S.Asghar,Journal of the Egyptian Mathematical Society 21(2013)379.

[3]M.Ramzan,M.Bilal,U.Farooq,and J.D.Chung,Results in Physics 6(2016)796.

[4]M.Ramzan,M.Farooq,A.Alsaedi,and T.Hayat,The European Physical Journal Plus 128(2013)49.

[5]M.Ramzan,M.Bilal,and J.D.Chung,Journal of Molecular Liquids 223(2016)1284.

[6]R.E.Powell,and H.Eyring,Nature(London)154(1944)427.

[7]N.S.Akbar,A.Ebaid,and Z.H.Khan,Journal of Magnetism and Magnetic Materials 382(2015)355.

[8]T.Hayat,M.Waqas,S.A.Shehzad,and A.Alsaedi,Journal of Aerospace Engineering 10.1061/(ASCE)AS.1943-5525.0000674(2016)04016077.

[9]M.Patel and M.G.Timol,Applied Numerical Mathematics 59(2009)2584.

[10]S.U.S.Choi,Enhancing Thermal Conductivity of Fluids with Nanoparticles,Developments and Applications ofNon-Newtonian,American Society of Mechanical Engineers,New York(1995)99.

[11]S.Nadeem and S.Saleem,Indian Journal of Pure&Applied Physics 52(2014)725.

[12]W.A.Khan,M.Khan,and R.Malik,PLoS ONE 9(2014)e105107.

[13]J.A.Khan,M.Mustafa,T.Hayat,and A.Alsaedi,International Journal of Heat and Mass Transfer 86(2015)158.

[14]B.Jalilpour,S.Jafarmadar,D.D.Ganji,A.B.Shotorban,and H.Taghavifar,Journal of Molecular Liquids 95(2014)194.

[15]M.Ramzan,M.Bilal,J.D.Chung,and U.Farooq,Results in Physics 6(2016)1072.

[16]M.Ramzan,F.Yousaf,M.Farooq,and J.D.Chung,Commun.Theor.Phys.66(2016)133.

[17]U.Khan,N.Ahmed,S.T.Mohyud-Din,and B.B.Mohsin,Neural Computing and Applications(2016)1;DOI 10.1007/s00521-016-2187-x.

[18]M.Sheikholeslami,M.M.Rashidi,T.Hayat,and D.D.Ganji,Journal of Molecular Liquids 218(2016)393.

[19]J.A.Khan, M.Mustafa, T.Hayat, and Alsaedi,Neural Computing and Applications(2016)1;DOI:10.1007/s00521-016-2743-4.

[20]T.Hayat,T.Muhammad,A.Alsaedi,and B.Ahmad,Results in Physics 6(2016)897.

[21]W.Ibrahim,The Effect of Induced Magnetic Field and Convective Boundary Condition on MHD Stagnation Point Flow and Heat Transfer of Nano fluid Over a Stretching Sheet,Nanotechnology,IEEE Transactions on,14(2015)178.

[22]G.Ib´a˜nez,International Journal of Heat and Mass Transfer 80(2015)274.

[23]M.Mustafa,J.A.Khan,T.Hayat,and A.Alsaedi,AIP Advances 5(2015)e027106.

[24]Q.Hussain,S.Asghar,T.Hayat,and A.Alsaedi,Journal of Central South University 22(2015)392.

[25]T.Hussain,S.A.Shehzad,A.Alsaedi,T.Hayat,and M.Ramzan,Journal of Central South University 22(2015)1132.

[26]M.B.Ashraf,T.Hayat,S.A.Shehzad,and A.Alsaedi,AIP Advances 5(2015)027134.

[27]M.Ramzan,M.Farooq,T.Hayat,and J.D.Chung,Journal of Molecular Liquids 221(2016)394.

[28]M.Ramzan M,Farooq M,S.Alhothuali,H.M.Malaikah,W.Cui,and T.Hayat,International Journal of Numerical Methods for Heat&Fluid Flow 25(2015)68.

[29]S.A.Shehzad,T.Hussain,T.Hayat,M.Ramzan,and A.Alsaedi,Journal of Central South University 22(2015)360.

[30]M.Ramzan,M.Farooq,T.Hayat,A.Alsaedi,and J.Cao,Journal of Central South University 22(2015)707.

[31]M.Ramzan,PLoS ONE 10(2015)e0124699.

[32]H.Zargartalebi,M.Ghalambaz,A.Noghrehabadi,and A.Chamkha,Advanced Powder Technology 26(2015)819.

[33]S.J.Liao,Beyond Perturbation,Chapman&Hall/CRC Press,Boca,Raton(2003).

[34]B.C.Sakiadis,AIChE J.7(1961)221.

[35]T.Hayat,Z.Iqbal,M.Qasim,and S.Obaidat,International Journal of Heat and Mass Transfer 55(2012)181.

[36]A.Aziz,Commun.Nonlinear Science and Numerical Simulation 14(2009)1064.