New Patterns of the Two-Dimensional Rogue Waves:(2+1)-Dimensional Maccari System∗

Gai-Hua Wang(王改华),Li-Hong Wang(王立洪),Ji-Guang Rao(饶继光),and Jing-Song He(贺劲松),†

1Department of Mathematics,Ningbo University,Ningbo 315211,China

2School of Mechanical Engineering&Mechanics,Ningbo University,Ningbo 315211,China

3School of Mathematical Sciences,University of Science and Technology of China,Hefei 230026,China

1 Introduction

Rogue waves(RWs)in the ocean are catastrophic natural phenomena with a long history and fascinating mariner stories,[1]which are also called as freak waves,monster waves,killer waves,extreme waves and abnormal waves.Recently,a growing consensus is that both oceanic and optical rogue waves[2−3]appear as a result of modulation instability of monochromatic nonlinear waves.The well known prototype of the RW in(1+1)-dimensional equation is the first-order RW solution of the NLS,which is also called Peregrine solution.[4]This fundamental solution has one large peak with three-times height of the asymptotical background surrounded by two deep hollows.There are many elegant patterns of the higher-order RWs constructed from the “brick”-the first order RW,which demonstrate the triangular,circular,triplet,pentagram,heptagram,claw-line,[5−8]etc. These rogue waves are localized in both space and time.Specifically,it arises from the background at very early stage of the evolution,then reaches the main peak(or maximum of amplitude)of the fundamental pattern or the area of strong interaction of other patterns mentioned in above,and eventually retreats back to the same background again.So rogue wave is often said that“appear from nowhere and disappear without a trace”.[9]The vivid feature of the firstorder rogue wave can be summarized as follows:[10](i)(quasi-)rational solution(or equivalently rational modulus of solution);(ii)localized doubly in both time and space;and(iii)large amplitude(the peak has a height at least three times of background)allocated with one hole in each side.In addition to the NLS equation,[11−16]rogue waves have also been found in other wave equations,such as the Hirota equation,[17−18]the complex modified Korteweg–de Vries(mKdV)equation,[19]the derivative NLS equations,[20−26]the Sasa-Satsuma equation,[27−28]the two-component NLS equations,[29−31]the threecomponent NLS equations,[32−33]“AB” system[34]and other equations.[10,35−39]These results show that RWs may be generic phenomena in nonlinear systems.

There are two propelling forces to study the RWs in two-dimensional-spatial and one-dimensional((2+1)-dimensional)temporal systems.The first is to explore the existence of the rogue waves in higher-dimensional space in order to extend the degree of the universality of the phenomena from the mathematical view. The second is originated from a realistic demand to establish the dynamical models with two spatial variables because of the two-dimensional nature of ocean RWs.Indeed,there are several(2+1)-dimensional equations such as the Davey–Ste warts on(DS)equation,[40−41]Yajima–Oikawa systems,[42]Fokas system,[43]which have rogue waves expressed by more complicated rational solutions.Above results show that the first-order RW in a(2+1)-dimensional equation is a line RW in(x,y)-plane,which is also used as“brick” to construct the higher-order RWs.The line pro file with two valleys of this fundamental(2+1)-dimensional RW generates gradually from a background,and then reaches the maximum around the timet=0,and finally decreases back into the background again.By comparing with the rich patterns[5−8]of the higher-order(1+1)-dimensional RWs,there just few patterns for the higher-order(2+1)-dimensional RWs,which is due to the complexity of the later,and the extreme difference between the interaction of their two “bricks”(i.e.,peak and line).However,recognizing new patterns of the(2+1)-dimensional RWs is useful to provide early warning of the ocean RWs.Thus,the(2+1)-dimensional RWs deserve further deep study with more efforts based on different methods.

In this paper,we focus on the new patterns of the RWs for the two-dimensional Maccari system,[44]that is

whereu≡u(x,y,t)andv≡v(x,y,t)represent a complex scalar field and a real scalar field,respectively.When“y=x”,it is similar[45](see its Eq.(6.6))to Zakharov equation[46]by a simple substitution,which is a model to describe the interaction between Langmuir(dispersive)and ion acoustic(approximately nondispersive)waves in a plasma.This fact provides a possible physical background of the two-dimensional Maccari system.Moreover,the nonlinear phenomena described by the Maccari system perhaps has connection with nonlinear waves of some models possessing modulated nonlinearities[47−48]and many methods can solve the nonlinear equations,such as Refs.[49–50].The Maccari system is derived by Maccari for the first time from the Kadomtsev–Petviashvili equation using asymptotically exact reduction method based on Fourier expansion and spatiotemporal re-scaling,and it is an integrable system because its Lax pair is obtained by applying the reduction technique to the Lax pair of the KP equation.[44]There are several kinds of solutions including periodic wave solutions and solitons for the Maccari system solved by several methods.[51−56]However,to the best of our knowledge,its lumps and rogue waves expressed by rational forms are still undisplayed in literatures.Therefore,the main purpose of the paper is to look for new patterns of the rogue waves from rational solutions of the Maccari system using the bilinear method.

The plan in the paper is as follows:In Sec.2,an explicit formula of the rational solution is expressed by determinants using the bilinear method,which is used to discuss the lumps and rogue waves.In Sec.3,the twelve new patterns of the rogue waves are given from the different combinations of the first-order line-rogue waves.In Sec.4,the summary and discussion on the main results are provided.

2 An Explicit Rational Solution in the Determinant Form

In this section,we shall construct an explicit formula of the rational solution for the Maccari system by bilinear method.To this end,set following variable transformation

wherefis a real function andgis a complex function,then Eq.(1)is transformed into two bilinear equations

Here“∗”denotes the complex conjugation,Dis a Hirota’s bilinear differential operator.[57]Note thatλis a constant of integration with respect toxand should be a function ofyandt,settingλ= −1 for the simpli fication of calculation in context.To avoid the confusion,we should stress that Maccari has introduced another twodimensional equation,[58−60]which is different from the Maccari system in this paper.

In order to get rational solutions ofuandvin the Maccari system,the first step is to obtainfandgin the polynomial forms by solving the bilinear forms in Eq.(3).Similar to the construction[61]of the rational solutions for the nonlinear Schrödinger equation,we have following theorem.

Theorem 1Two polynomial solutionsfandgof bilinear equations(3)are expressed byN×Ndeterminants,

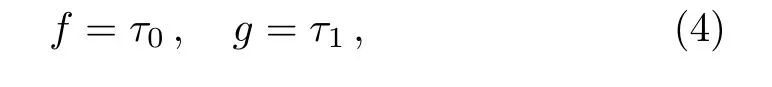
where

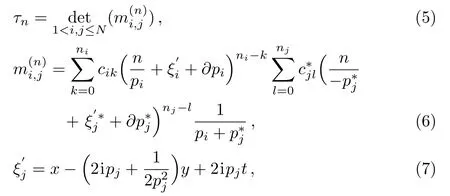
andpi,cik,cjlare arbitrary complex constants,butniandnjare two arbitrary non-negative integers.

The proof of the theorem is given in Appendix.Substitutingfandggiven by theorem 1 back into Eq.(2),it yields an explicit formula of the rational solutions for the Maccari system.By a scaling offandg,setci0=1 in solutions of the next section without loss of generality.From now on,pjRdenotes the real part ofpj,andpjIdenotes the imaginary part ofpjfor the convenience.

3 New Patterns of the Rogue Wave for Maccari System

In this section,twelve new patterns of the rogue waves will be given from the fundamental rational solutions ofN=1 and multi-rational solutions ofN≥2 based on Theorem 1 and Eq.(2).

3.1 The First-Order Rational Solution

SetN=1 andni=nj=n1=1,then theorem 1 providesfandgin bellow:

Here=x−(2ip1+1/)y+2ip1t,c10=1,parametersp1andc11are two arbitrary complex constants.

Settingp1=p1R+ip1I,c11=c11R+ic11Iand simplifying the expressions offandg,then

Taking abovefandginto Eq.(2),thenuandvare two first-order rational solutions of the Maccari system,and given explicitly by

These solutions are classified two categories:lump and line-rogue wave.

(i)Lump solutions.Whenb2/=0,one can see thatuandvare constants along the trajectory[x(t),y(t)]where

and(u,v)→ (1,0)as(x,y)→ (∞,∞)at arbitrarily given time.So,lump solutions can not disappear along time

evolution but propagate with a significant amplitude on the constant background.

In general,patterns on(x,y)-plane around the momentt=0 are very clear and remarkable,for above rational solutionsuandv.In order to discuss the different patterns,it is useful to calculate the all possible critical points of|u|2att=0.By a simple calculation,there are five possible critical points,i.e.,

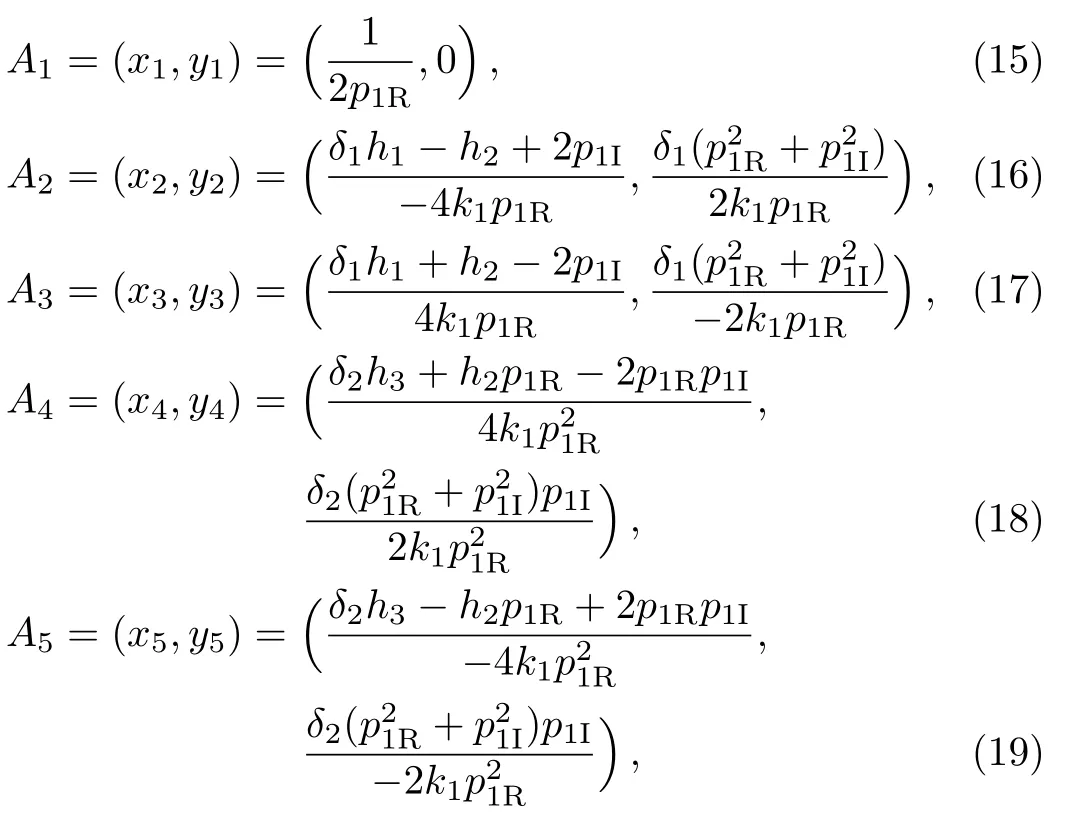
which are solved by∂|u|2(0,x,y)/∂x=∂|u|2(0,x,y)/∂y=0.Here

Further,three kinds of second-order derivative of|u|2are:H1=∂2|u|2/∂x2,H2=∂2|u|2/∂y2,H3=∂2|u|2/∂x∂yandH=H1H2−.A tedious calculation infers

Here

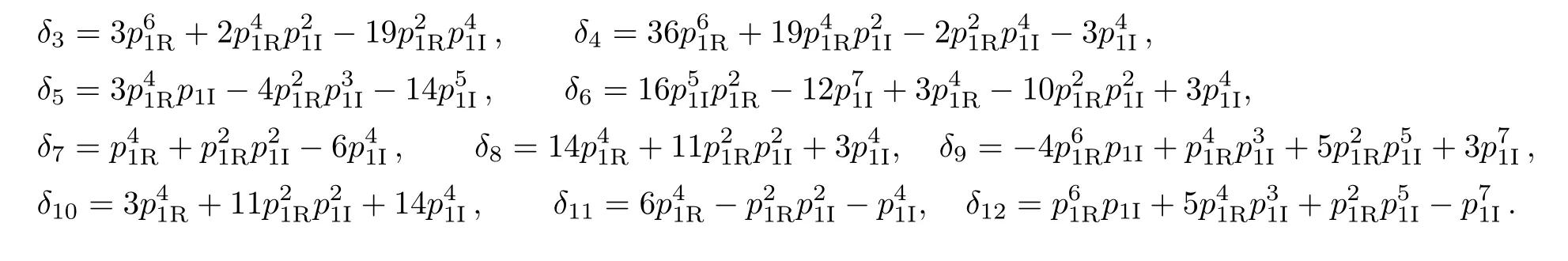
According toAi(1≤i≤5),H1andH,the lump solutionsuin Eqs.(12)can be classified into three patterns.

(a)Bright lump.When 0≤≤(1/3)|u|has one local maximum(pointA1)and two local minimum points(pointA4andA5);

(b)Bi-model lump.When(1/3)＜＜,|u|has two local maximums points(pointA2andA3)and two local minimum points(pointA4andA5);

(c)Dark lump.When≥,|u|has two local maximums(pointA2andA3)and one local minimum point(pointA1).These extreme points are con firmed in the pro files of single-lump plotted in Fig.1 of|u|given by Eq.(12).

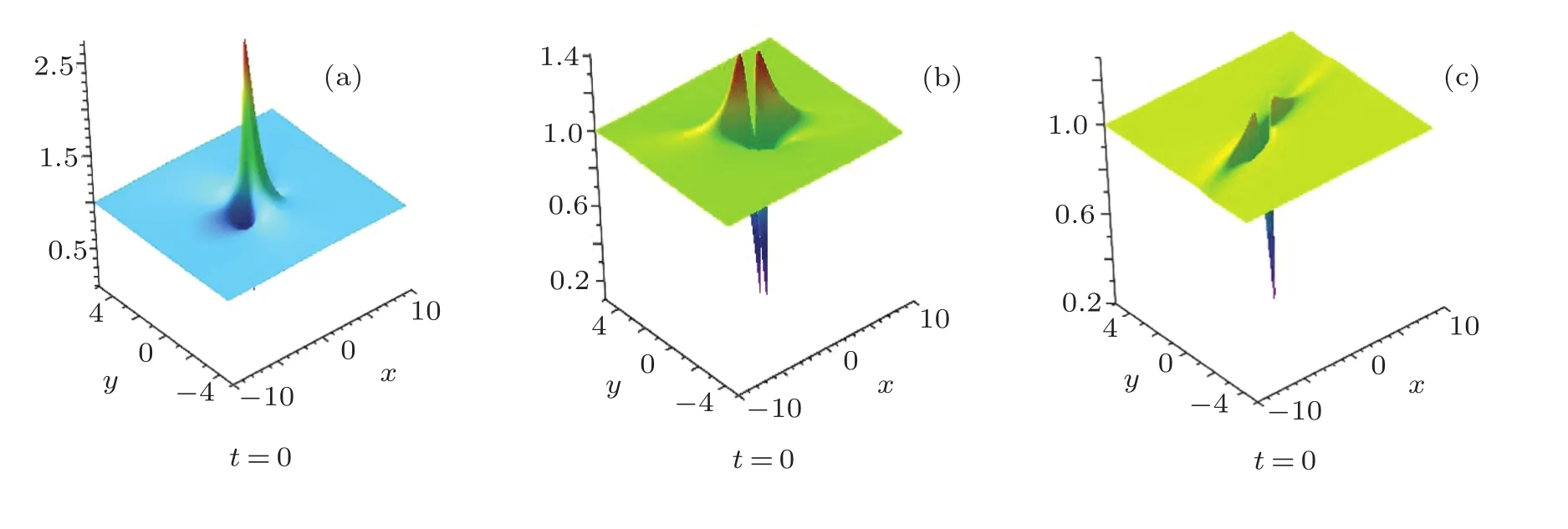
Fig.1 Three patterns of a single-lump|u|in Eq.(12)at t=0 with different parameters.(a)A bright lump with p1R=1,p1I=1/4;(b)A bi-modal lump with p1R=1,p1I=1;(c)A dark lump with p1R=−1,p1I=−2.

(ii)Rogue wave solution

It is well-known that the rogue wave solution is a special case of the rational solution under certain constraint conditions.Setb2=0,namely

then rational solutionuin Eq.(12)is a line-rogue wave.It arises from the constant background with a line pro file at early stage,then reaches a peak(or valley)aroundt=0,and finally retreats back to the same background.This shows that the large amplitude in the pro file of the line-rogue wave exists a short period of time,which is different from a moving line-soliton on(x,y)-plane for two-dimensional integrable equations.The validity of the evolution of the line-rogue wave is demonstrated in Fig.2.

The line rogue wave can be classified into three patterns according to the distribution of the critical lines.The rogue wave solution|u|2in Eq.(12)underb2=0 has possible five critical lines,which are calculated from∂|u|2/∂y=∂|u|2/∂t=0 and expressed by

Here

Fig.3 A line-rogue wave|u|in Eq.(12)with p1R=1/2,p1I=1/2,which is vanished when t=0.This pattern is very particular by comparing with common line-rogue wave which reaches usually a large amplitude at t=0.When|t|≥20,this wave disappears into the background.

Three patterns of line-rogue wave are listed by bright line-rogue wave,intermediate state line-rogue wave and dark line-rogue wave,which are plotted in three rows of Fig.2,respectively.

(i)The bright line-rogue wave in the first row.It attains its maximum lineL1with height 3,which is three times the height of background,and minimum 0 at two linesL4andL5.This is a common line-rogue wave in the two-dimensional equations possessing one maximum line and two minimum lines in two sides.[40−42]This wave disappears into the background when|t|≥180.

(ii)The intermediate state line-rogue wave in the second row.It has one maximum line(L2orL3)and one minimum line(L4orL5)fort/=0.However,it becomes a bright line-rogue wave att=0 with one maximum lineL1and two minimum lines.Under the choices of parameters in this row,its maximum reaches 1.9183 atL2fort＜0 andL3fort＞0,the minimum is 0 atL4andL5fort/=0.The one local maximum is 1.9128 atL1fort=0 and this wave is vanished into the background when|t|≥20.Note that intermediate state line-rogue wave is given firstly in the Yajima–Oikawa systems.[42]

(iii)The dark line-rogue wave in the third row.It has one maximum line(L2orL3)and one minimum line(L4orL5)fort/=0,as the intermediate state line-rogue wave.However,it becomes a downward wave att=0 with two maximum lines and one deep minimum line,which is different from the latter.Under the choices of parameters in this row,it attains maximum 1.2819 atL2andL3,the minimum attitude 0 atL4andL5fort/=0.Meanwhile,the minimum is 0.5656 atL1fort=0.This wave disappears into the background when|t|≥20.

According to above analysis,the difference between the bright and intermediate state RWS is the number of the line of extreme values whent/=0.However,the valley of the dark rogue wave is much deeper than the intermediate state RW.In particular,whent=0,both of them have three lines of the extreme values,the former has a significant downward amplitude,but the latter has a dominant upward amplitude.The dark line-rogue wave in the third row of Fig.2 of Ref.[42]has one minimum line and two maximum lines.Thus the dark line-rogue wave in our paper is a new pattern.

Further,the pattern of|u|withp1R=1/2,p1I=1/2 in Fig.3 is new,although it has one maximum line and one minimum line whent/=0 as the second and third rows in Fig.2 because it is vanished whent=0.

3.2 Multi-rogue Wave Solutions with N=2

In the above subsection,we have studied the fundamental rational solution ofu,i.e.,the first-order solution,which is the simplest case.SettingN≥2,n1=n2=···=nN=1 in theorem 1 and the constraint conditions:

then Eq. (2)generates one kind of special nonfundamental rational solution,which is called multirogue.[40]Here Im represents the imaginary part of a function and(pj)is defined by

andpjis an arbitrary complex constant.

In order to get the simplest multi-rogue wave,settingN=2 in Theorem 1,thenfandgcan be written out as

and(34)into Eq.(2),thenuandvare two two-rogue waves.For this case,two solutionsuandvapproach to the constant background uniformly in the entire(x,y)-plane whent→±∞.In the intermediate time,there will occur two line-rogue waves,which arise from the constant background,interact with each other,and disappear into the background again.

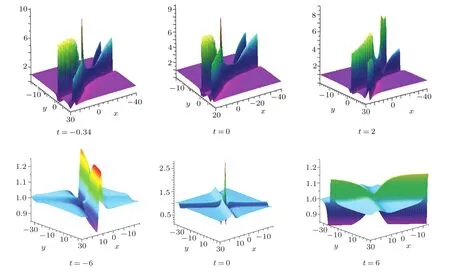
Fig.4 The evolution of two patterns for the two-rouge wave|u|.The first row is plotted for a bright-intermediate rogue wave|u|with p1I=1/500,p2I=1/20.The second row is plotted for an intermediate-intermediate rogue wave|u|with p1I=1/4,p2I=1/2.

To illustrate the evolution of the two-rogue wave clearly,two patterns are displayed in Fig.4.This figure shows remarkably in the intermediate time that an X-shape signature appears in the(x,y)-plane,which is generated by the strong interaction of the two line-rogue waves.One of them is oriented along they-direction and the other is oriented along thex-direction.Furthermore,Fig.4 also demonstrates that one two-rogue wave disappears indeed without a trace for sufficient large time,i.e.|t|＞150 in the first row and|t|＞30 in the second row.The first row is a bright-intermediate state rogue wave which consists of one bright line-rogue wave oriented along thex-direction and one intermediate state line-rogue wave oriented along they-direction.When|t|is small,the intermediate state line-rogue wave still always have a maximum line and a valley similar to the evolution in the second row of Fig.2.The pattern given by the first row has been discovered for Yajima–Oikawa systems[42](see the third row of Fig.3 in this reference).The second row is an intermediate-intermediate state rogue wave consisting of two intermediate state line-rogue waves.It clearly displays that two fundamental line-rogue waves arise from the constant background and finally decrease back again into the same background for large timet.When|t|≤6,there exists two remarkable amplitudes of the wave.In particulart=0,its amplitude acquires the maximum,which is larger than the maximum of a single line-rogue wave because of the strong interaction of two line-rogue waves.At last,it is interesting to see from Fig.4 that the orientation of every line-rogue wave in two-rogue wave is preserved very well during the evolution with time,which shows visually the independence of two line-rogue waves.

It is natural to explore more patterns in the two-rogue wave generated by the different combinations of the three fundamental line-rogue wave in Fig.2.Four patterns are plotted in Fig.5 with the help ofuin Eq.(2),fandgin Eqs.(33),(34),and the constraint in Eq.(31).These patterns of the two-rogue wave are bright-dark,bright-bright,intermediate-dark,and dark-dark,in Fig.5 from(a)to(d)in order.To save the space,we just provide the pro files of them att=0.There are three new patterns in(a),(c),and(d),because all of them have one new dark-line rogue wave in Fig.2.

3.3 Multi-Rational Rogue Wave Solutions with N=3

In this subsection,three-rogue wave is generated fromuin Eq.(2),fandgin Eq.(4)withN=3,and the constraint in Eq.(31).Six new patterns of three-rogue waves are plotted in Fig.6 according to this way.They are more complicated combinations of three fundamental line-rogue waves given by Fig.2.The parameters of them in order are:(a)p1I=1/200,p2I=1/500,p3I=4/7;(b)p1I=1/200,p2I=3/4,p3I=4/7;(c)p1I=1/200,p2I=1/3,p3I=2/3;(d)p1I=1/4,p2I=1/3,p3I=3/4;(e)p1I=4/7,p2I=3/4,p3I=2/3;(f)p1I=4/7,p2I=3/4,p3I=1/3.

Fig.5 Four patterns of the two-rouge wave|u|.(a)The bright-dark rogue wave with p1I=1/640,p2I=3/4;(b)The bright-bright rogue wave with p1I=1/500,p2I=1/200;(c)The intermediate-dark rogue wave with p1I=1/2,p2I=3/4;(d)The dark-dark rogue wave with p1I=2/3,p2I=4/7.

Fig.6 Six new patterns of three-rogue wave for|u|at t=0.(a)The bright-bright-dark rogue wave;(b)The bright-dark-dark rogue wave;(c)The bright-intermediate-dark rogue wave;(d)The intermediate-inter mediate dark rogue wave;(e)The dark-dark-dark rogue wave;(f)The intermediate-dark-dark rogue wave.

4 Summary and Discussions

We have derived an exact explicit formula of the rational solutionuandvin Eqs.(2)and(4)for the Maccari system by the bilinear method.The rational solution includes one kind of lump solution and one kind of rogue wave.Furthermore,we have discussed extreme pointsAi(i=1,2,···,5)of the first-order lumps and the extreme linesLi(i=1,2,···,5)of the first-order rogue waves.We have found twelve new patterns,see the third row of Fig.2,Fig.3,the second row of Fig.4,Figs.5(a),5(c),and 5(d).Fig.6,of the(2+1)-dimensional rogue wave.The conditionb2=0 in the first-order rational solution and Eq.(31)in the higher-order rational solution are crucial to generate the first-order rogue wave and the multi-rogue waves.

In general,the higher-order rational solution of a twodimensional equation can generate higher-rogue wave besides the multi-rogue wave.[40−43,60]Note that the condition to generate higher-rogue waves in Refs.[40–43,60]does not work out the expected higher-rogue waves of the Maccari system.We shall continue the study on this problem in the future.

Appendix

In this appendix,we provide a simple proof of Theorem 1 by the bilinear transformation method based on the results of Ref.[61].

Lemma 1The bilinear equations

admit determinant solution

Hereξi=pix1+x2+(1/pi)x−1,pi,cikare complex constants.AiandBjare differential operators of orderniandnjwith respect topiand.niandnjare non-negative integers.

This Lemma can be proved by the same method as for Lemma 3.1 in Ref.[61],thus its proof is omitted here.Settingτ(0)=f,τ(1)=g,τ(−1)=g∗,and taking the independent and dependent variables as

meanwhile imposing the complex conjugate conditions

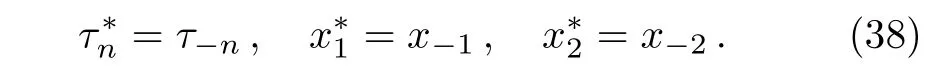
then Eq.(35)is transformed into the bilinear Eq.(3).Therefore,according to Lemma 1 and Eq.(37),we get formula(4).This ends the proof of Theorem 1.

Acknowledgment

We thank the members of our group at Ningbo University for the useful suggestions and discussions on the draft of this paper.

References

[1]P.C.Liu,Geo fizika,24(2007)57.

[2]C.Kharif,E.Pelinovsky,and A.Slunyaev,Rogue Waves in the Ocean,Springer,Beilin(2009).

[3]D.R.Solli,C.Ropers,P.Koonath,and B.Jalali,Nature(London)450(2007)1054.

[4]D.H.Peregrine,J.Austral.Math.Soc.Ser.B 25(1983)16.

[5]D.J.Kedziora,A.Ankiewicz,and N.Akhmediev,Phys.Rev.E 85(2012)066601.

[6]J.S.He,H.R.Zhang,L.H.Wang,K.Porsezian,and A.S.Fokas,Phys.Rev.E 87(2013)052914.

[7]D.J.Kedziora,A.Ankiewicz,and N.Akhmediev,Phys.Rev.E 88(2013)013207.

[8]L.M.Ling and L.C.Zhao,Phys.Rev.E 88(2013)043201.

[9]N.Akhmediev,A.Ankiewicz,and M.Taki,Phys.Lett.A 373(2009)675.

[10]D.Q.Qiu,Y.S.Zhang,K.Porsezian,and J.S.He,Proc.R.Soc.A 471(2015)20150236.

[11]N.Akhmediev,A.Ankiewicz,and J.M.Soto-Crespo,Phys.Rev.E 80(2009)026601.

[12]P.Dubard,P.Gaillard,C.Klein,and V.B.Matveev,Eur.Phys.J.Spec.Top 185(2010)247.

[13]P.Dubard and V.B.Matveev,Nat.Hazards&Earth Syst.Sci.11(2011)667.

[14]P.Gaillard,J.Phys.A:Math.Theor.44(2011)4109.

[15]D.J.Kedziora,A.Ankiewicz,and N.Akhmediev,Phys.Rev.E 84(2011)056611.

[16]B.L.Guo,L.M.Ling,and Q.P.Liu,Phys.Rev.E 85(2012)026607.

[17]A.Ankiewicz,J.M.Soto-Crespo,and N.Akhmediev,Phys.Rev.E 81(2010)046602.

[18]Y.S.Tao and J.S.He,Phys.Rev.E 85(2012)026601.

[19]J.S.He,L.H.Wang,L.J.Li,K.Porsezian,and R.Erd´elyi,Phys.Rev.E 89(2014)062917.

[20]S.W.Xu,J.S.He,and L.H.Wang,J.Phys.A:Math.Theor.44(2011)305203.

[21]S.W.Xu,J.S.He,and L.H.Wang,EPL 97(2012)29903.

[22]B.L.Guo,L.M.Ling,and Q.P.Liu,Stud.Appl.Math.130(2012)317.

[23]H.N.Chan,K.W.Chow,D.J.Kedziora,R.H.Grimshaw,and E.Ding,Phys.Rev.E 89(2014)032914.

[24]L.J.Guo,Y.S.Zhang,S.W.Xu,Z.W.Wu,and J.S.He,Phys.Scr.89(2014)035501.

[25]Y.S.Zhang,L.J.Guo,J.S.He,and Z.X.Zhou,Lett.Math.Phys.105(2015)853.

[26]Y.S.Zhang,L.J.Guo,A.Chabchoub,and J.S.He,Commun.Nonlinear Sci.Numer.Simul.19(2014)1706.

[27]U.Bandelow and N.Akhmediev,Phys.Rev.E 86(2012)026606.

[28]S.H.Chen,Phys.Rev.E 88(2013)023202.

[29]B.L.Guo and L.M.Ling,Chin.Phys.Lett.28(2011)110202.

[30]F.Baronio,A.Degasperis,M.Conforti,and S.Wabnitz,Phys.Rev.Lett.109(2012)044102.

[31]B.G.Zhai,W.G.Zhang,X.L.Wang,and H.Q.Zhang,Nonlinear Anal.Real World Appl.14(2013)14.

[32]L.C.Zhao and J.Liu,Phys.Rev.E 87(2013)013201.

[33]Z.Y.Qin and G.Mu,Phys.Rev.E 86(2012)036601.

[34]C.F.Wu,R.H.J.Grimshaw,K.W.Chow,and H.N.Chan,Chaos 25(2015)103113.

[35]F.Baronio,M.Conforti,A.Degasperis,and S.Lombardo,Phys.Rev.Lett.111(2013)114101.

[36]A.Ankiewicz,Y.Wang,S.Wabnitz,and N.Akhmediev,Phys.Rev.E 89(2014)012907.

[37]X.Wang and Y.Chen,Chin.Phys.B 23(2014)070203.

[38]F.Baronio,S.H.Chen,P.Grelu,S.Wabnitz,and M.Conforti,Phys.Rev.A 91(2015)033804.

[39]A.Degasperis,S.Wabnitz,and A.B.Aceves,Phys.Lett.A 379(2015)1067.

[40]Y.Ohta and J.K.Yang,Phys.Rev.E 86(2012)036604.

[41]Y.Ohta and J.K.Yang,J.Phys.A:Math.Theor.46(2013)105202.

[42]J.C.Chen,Y.Chen,B.F.Feng,and K.I.Maruno,Phys.Lett.A 379(2015)1510.

[43]J.G.Rao,L.H.Wang,Y.Zhang,and J.S.He,Commun.Theor.Phys.64(2015)605.

[44]A.Maccari,J.Math.Phys.37(1996)6207.

[45]J.Bourgain,Duke Math.J.76(1994)175.

[46]V.E.Zakharov,JETP 35(1972)908.

[47]S.L.Xu and M.R.Beli,J.Opt.Soc.Am.B 30(2013)2715.

[48]S.L.Xu,J.X.Cheng,M.R.Beli,Z.L.Hu,and Y.Zhao,Opt.Express 24(2016)10066.

[49]Z.Z.Zhang,Turkish J.Phys.32(2008)235.

[50]X.J.Miao and Z.Y.Zhang,Commun.Nonlinear Sci.Numer.Simul.16(2011)4259.

[51]K.Porsezian,J.Math.Phys.38(1997)4675.

[52]S.Zhang,Phys.Lett.A 371(2007)65.

[53]D.Rostamy,F.Zabihi,K.Karimi,and S.Khalehoghli,Appl.Math.2(2011)258.

[54]A.M.Wazwaz,Phys.Scr.85(2012)65011.

[55]H.Kumar and F.Chand,J.Theor.Appl.Phys.8(2014)114.

[56]S.T.Demiray,Y.Pandir,and H.Bulut,Ocean Eng.103(2015)153.

[57]R.Hirota,The Direct Method in Soliton Theory,Cambridge University Press,Cambridge(2004).

[58]A.Maccari,J.Math.Phys.38(1997)4151.

[59]W.H.Huang,Y.L.Liu,and Z.Y.Ma,Commun.Theor.Phys.47(2007)397.

[60]F.Yuan,J.G.Rao,K.Porsezian,D.Mihalache,and J.S.He,Rom.J.Phys.61(2016)378.

[61]Y.Ohta and J.K.Yang,Proc.R.Soc.A 468(2012)1716.