基于滑模控制的大型变速风机的最大风能捕获研究

曾令全，王美琪，张佳琦，冯天舒

(东北电力大学 电气工程学院，吉林 吉林 132012)



基于滑模控制的大型变速风机的最大风能捕获研究

曾令全，王美琪，张佳琦，冯天舒

(东北电力大学 电气工程学院，吉林 吉林 132012)

为了解决当风力发电机参数辨识错误或有扰动误差时，最大风能捕获策略出现的风能利用率下降问题，根据已知的风力发电机特性和滑模变结构系统理论，提出了在低于额定风速条件下，变速风力发电机的非线性反馈控制方案。通过使用带有风速估计的滑模控制器，利用转速值进行最大风能捕获。构建系统模型进行仿真并与传统控制策略进行分析比较，结果证实了文中控制策略的正确性和有效性。

滑模控制；变速风力发电机；最大风能捕获；非线性控制

由于人口膨胀和全球一体化加速发展，能源消耗快速增长[1]。作为一种极具潜力的清洁能源，风力发电近年来受到普遍重视[2]，随着世界能源紧缺问题的突出，可再生能源发电的需求也相应增加，风电系统的运行效率越来越受到关注[3]。

变速风力发电机的运行可分为三个区域[4]：

区域I：低于切入风速。

区域II：在切入风速和额定风速之间。

区域III：在额定风速和切出风速之间。

本文主要针对区域II进行研究。对于低风速下的最大风能捕获，学者们做了大量研究[5]。尽管一些传统方法已经得到成功的应用[6]。但由于风速的不确定性、随机性以及风力发电机的非线性、多变量、大惯性等特点，传统的线性控制策略难以准确跟踪变化的风速并且严格跟踪最优转速又会提高系统的转矩波动，增加传动系统的机械载荷。传统方法并未考虑控制器的非线性以及风能与风力发电机的动态特性[7]。

当前，风力发电机的非线性控制一直受到学术界的关注，如滑模变结构控制[8]。这种方法能够抑制参数不确定性、外部干扰和未建模动态，并且具有有限时间可达性的特点[9]。本文通过对风力发电机特性及最大风能捕获的原理分析，提出了基于准连续滑模控制方法的控制策略，设计了一个基于超扭曲算法[10]和牛顿-拉夫逊算法的风速估计方法，根据滑模控制算法，使用一阶滑模控制器解决假设所有状态均可测量条件下的功率优化问题，并应用准连续二阶滑模控制器降低抖振对发电机转矩的影响。最大限度地提高风能捕获能力并减少风力发电机的机械应力，有效改进了传统的控制策略。

1 风力发电机模型及最大风能捕获原理

风力发电机模型包含气动特性、风力机机械特性以及发电机动态特性[11]。

1.1 气动特性

风力发电机捕获的风能可以表示为[12]：

(1)

式中：v(t)为风速；为空气密度；R为叶片半径；Cp为风能利用系数，是取决于叶片桨距角β以及叶尖速比的非线性函数，其关系曲线如图1所示。叶尖速比与叶尖圆周速度与风速之比：

(2)

其中：ωr为转子转速。

Pa=Taωr，

(3)

式中：Ta为取决于叶尖速比的非线性气动扭矩。

(4)

图1 风能利用系数曲线

1.2 机械特性

风力机将风能转换为机械能，并通过传动系统将所得能量传递给发电机，其运动方程描述如下[9]：

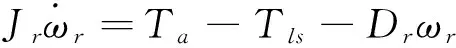
(5)

式中：Jr和Dr分别为风力机的转动惯量、阻尼系数；Tls为低速轴转矩。

发电机将吸收的机械能转变为电能形式输出，发电机受高速轴和电磁转矩的共同作用，其运动方程为：

(6)

式中：Jg和Dg分别为发电机的转动惯量、阻尼系数；ωg为发电机转速；Ths为高速轴转矩；Te为电磁转矩。

联立式(5)、式(6)，可得变速风力发电机两质量动力学模型如下：

(7)

式中：ωls为低速轴转速；ωr为转子角偏差；θls为变速箱角偏差；Dls为低速轴阻尼；Kls为低速轴刚度；δ为主轴误差。假定传动齿轮及低速轴为绝对刚性，则有：

(8)

式中：ng为齿轮箱传动比，Tls为低速轴转矩。

若ωr=ωls，可将风力发电机视作一个简单的刚体模型。联立公式(7)、公式(8)，可以得到其运动方程如下：

(9)

1.3 最大风能捕获原理

根据贝兹理论，由公式(1)可知，在风速v一定的情况下，风力机获得的机械功率的大小将只取决于风能转换系数Cp。在低风速下，β保持最佳值βmax不变，此时最大风能转换系数Cpmax(opt，βopt)只取决于最佳叶尖速比λopt。

由公式(2)可得最佳叶尖速比：

(10)

最大风能利用系数：

CP(λopt，βopt)=CPmax.

(11)

为了保证风力发电机捕获最大风能，桨距角β固定在βmax，而ωropt的值应随风速的变化而改变，确定相应的ωropt使气动功率保持在最大值。

(12)

为检验所提出控制器的性能，与参考文献[13]中的三种控制器进行了比较，三种控制策略控制方程如下：

间接速度控制(ISC)：

(13)

非线性静态反馈控制(NSSFC)：

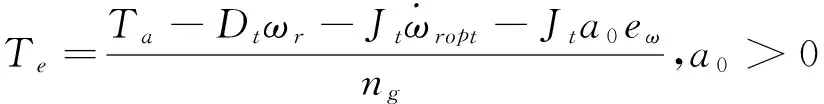
(14)

其中，eω=ωropt-ωr是转子转速误差。

非线性动态反馈控制(NDSFC)：

(15)

2 基于滑模控制的最佳转矩法

基于以上理论分析，结合一阶和二阶滑模控制策略，提出了带有风速估计的滑模控制器。控制策略框图，如图2所示。

图2 最佳转矩法控制策略

2.1 风速预测

(16)

风速估计结果见图3、图4所示。图3为实际风速曲线，图4为相应的估计风速曲线。可见，风速估计值接近实际风速，风速估计器实现了较好的风速估计。存在的误差主要由未建模动态、Cp曲线误差、动态效应导致的幂函数变化及牛顿-拉夫逊算法的收敛速度导致。基于有效估计风速，根据风轮转速与叶尖速比的关系，可以得到最佳转子速度：

. (17)

2.2 一阶滑模控制器

根据最大风能捕获原理及公式(9)、公式(10)，选择控制系统状态变量为x=[ωrTa]，控制输出变量u=Te。一阶滑模控制器(FOSMC)，选取转子转速误差作为滑模变量：

(18)

将公式(18)对时间求导，联立等式(9)，可得一阶滑模控制器控制方程如下：

(19)

(20)

2.4 二阶滑模控制器

为实现风力发电机气动功率提取效率最大化，进一步设计了二阶滑模控制器(SOSMC)。由二阶动力学方程：

(21)

将滑模变量及其二阶导数代入公式(21)，可以得到：

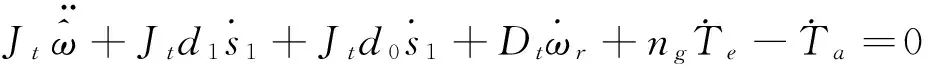
(22)

将公式(20)代入公式(22)，整理可得二阶滑模控制器控制方程如下：

(23)

上述控制需用到s1的时间导数λ1，通过一个由一阶实时微分器组成滑模微分器估计得到，其形式如下：

(24)

式中：z0和z1分别为s1和λ1的实时估计值。

2.3 稳定性分析

滑模控制律应满足李雅普诺夫稳定条件，考虑李雅普诺夫函数：

(25)

系统稳定时，李雅普诺夫函数应满足：

(26)

(27)

3 紊流风下的仿真

基于上述理论分析，应用MATLAB/Simulink搭建水平轴风力发电机的动力学模型[15-17]，对控制器的稳态性能进行了相关仿真分析，并通过dSPACE半物理仿真平台对控制器控制的动态性能进行了验证。

3.1 仿真参数

风速可视为由一个快速变化的紊流风速与缓慢变化的均匀风速的叠加值。

测量点处风速v的模型为：

v=vm+vt，

(28)

式中：vm为平均风速，vm=7.5 m/s；vt为紊流风速。湍流强度为18%，仿真时间为600 s。

为控制器选取参数如下：a0=0.115，b0=0.000 5，b1=0.040 2，a1=4.746×104，α1=389.094 7，d0=0.000 5，d1=0.040 2，α2=19.454 7，Kopt=5.381 3×103。

初始条件如下：Te(0)=1 408.591 9 Nm，q=100，ωr(0)=33.7042 rad/s，ωg(0)=1 454.841 7 rad/s。

3.2 仿真结果

所设计的控制器主要用于提高最大风能捕获效率并减小发电机转矩波动，避免风力发电机机械应力的增加，基于MATLAB/Simulink的仿真结果如下所示。

图5 转子转速曲线

通过图5至图8对比分析各控制器的控制性能，可以分析得到，在一般情况下，ISC控制器的控制性能最低。转子转速和发电机转速如图5和图6所示。仿真结果显示，一阶滑模控制(SOSMC)和非线性动态反馈控制(NDSFC)更接近最佳转子速度，并且避免了短时间紊流成分的干扰。由于间接速度控制(ISC)和非线性静态反馈控制(NSSFC)不能控制干扰输入，相对其它控制器，其追踪风速的效果较差，因此加大了风能捕获中的风能损失。

图6 风力发电机转速曲线

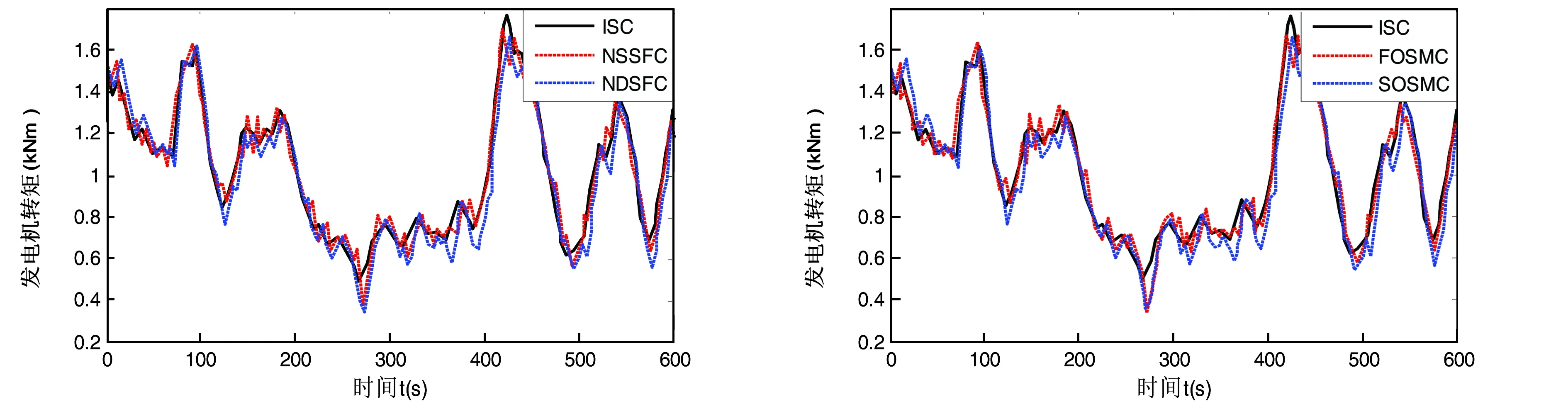
图7 风力发电机输出转矩曲线

观察风力发电机输出转矩曲线(见图7)可知，相比于其他控制器，一阶滑模控制器(FOSMC)获得的输出转矩更大。观察图8可知，通过一阶滑模控制(FOSMC)获得的功率要高于通过非线性静态反馈控制(NSSFC)得到的功率，但是要低于非线性动态反馈控制(NDSFC)；而二阶滑模控制(SOSMC)在能量转换方面明显优于非线性动态反馈控制(NDSFC)。

图8 风力发电机输出有功功率曲线

3.2 实验结果

基于dSPACE半物理仿真平台，对上述控制器控制性能进行了验证。评价控制器性能的指标为：空气动力学效率ηaero和电能效率ηelec，发电机电磁转矩Te标准差及最大值，以及低速轴转矩Tls标准差及最大值。空气动力学效率及电能效率定义如下[18]：

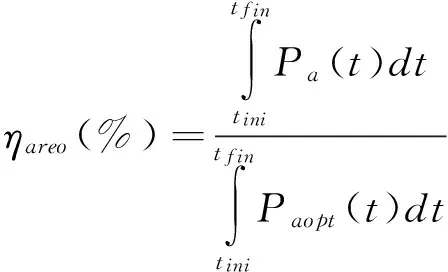
(29)

其中：Paopt=0.5ρπR2CPmaxv3是相应于风速的最优气动功率；Pe=Teωg。控制器的性能参数详见表3。

基于dSPACE半物理仿真平台测试结果，观察表3，如前分析所述，间接速度控制(ISC)的各项性能指标最低，控制性能最差。间接速度控制(ISC)和非线性静态反馈控制(NSSFC)因不能抵制干扰输入导致追踪风速性能较差。然而相比于其他控制器，采用二阶滑模控制(SOSMC)进行控制，其空气动力学效率ηaero及电能效率ηelec均为最大值，并且max(Te)和std(Te)均为最低值表明该控制策略具有更好的动态特性，其max(Tls)及std(Tls)值也为最小，表明低速轴机械应力较低。

表3 控制器实验参数列表

4 结 论

本文主要解决基于风速估计的变速风力发电机的发电控制问题。提出了一种带有风速估计器的滑模控制策略，进行最大风能捕获，同时减少机械载荷。通过Matlab/Simulink对控制策略进行了仿真研究，结果表明，与传统控制策略相比，该控制策略能够更好地控制风力机转速以准确跟踪风速变化，保持最佳叶尖速比，保证了更好的风能捕获效率，并在实现最大风能捕获的同时，降低了发电机的电磁转矩波动幅度，实现了提高效率同时降低载荷的多目标优化控制目的，能够合理的平衡转换效率、机械压力及扰动抑制三者之间的关系。基于dSPACE半物理仿真平台的系统模型验证表明了该策略的可行性。

[1] 迟永宁，刘燕华，王伟胜，等.风电接入对电力系统的影响[J].电网技术，2007，31(3)：77-81.

[2] 李践飞，张敬南，简杰.双馈风力发电系统最大风能捕获控制研究[J].船电技术，2014，34(4)：1-4.

[3] 张淼，陈治平，陈思哲，等.孤岛双馈风力发电机组最大风能捕获策略[J].特微电机，2015，43(1)：46-49.

[4] 耿华，杨耕，周伟松.考虑风机动态的最大风能捕获策略[J].电力自动化设备，2009，29(10)：107-111.

[5] 张文娟，高勇，杨媛.基于风力机参数辨识的最大风能捕获[J].电网技术，2009，33(17)：152-156.

[6] 刘立群，王志新，张华强，等.分布式风力发电系统MPPT控制[J].电力自动化设备，2011，31(8)：6-10.

[7] 张志，王清灵，朱一凡，等.变速恒频双馈风力发电系统最大风能捕获控制[J].电机与控制应用，2010，37(3)：18-21.

[8] 徐红，刘东乐.基于观测器的风力发电系统滑模变结构控制[J].电力系统及其自动化学报，2013，25(2)：20-24.

[9] 赵亮，韩华玲，陈宁，等.基于模糊滑模控制的风电机组最大风能追踪策略[J].电力自动化设备，2012，32(12)：74-79.

[10] C.Evangelista，P.Puleston，F.Valenciaga，et.Lyapunov-designed super-twisting sliding mode control for wind energy conversion optimization[J].IEEE Trans Ind Electron，2013，60(2)：538-545.

[11] 刘先正，王兴成，温家良，等.风力发电机组动力学建模与分析[J].电力系统自动化，2015，39(5)：15-19.

[12] 李东东，陈陈.风力发电机组动态模型研究[J].中国电机工程学报，2005，25(3)：115-119.

[13] B.Boukhezza，H.Siguerdidjane.Nonlinear control of variable speed wind turbines without wind speed measurement[C].44th IEEE Conference on Decision and Control，and European Control Conference(CDC-ECC＇05)，Serbia，Spain，2005.

[14] B.Boukhezzar，H.Siguerdidjane.Comparison between linear and nonlinearcontrol strategies for variable speed wind turbines[J].Control Engineering Practice，2010，18(12)：1357-1368.

[15] 严干贵，李鸿博，崔杨，等.基于等效风速的风电场等值建模[J].东北电力大学学报，2011，31(3)：13-19.

[16] 张帆，李国庆，张宇阳，等.双馈感应风电机组建模控制仿真[J].东北电力大学学报，2011，31(4)：80-85.

[17] 祝贺，许大田，赵浩然，等.双馈风电机组PWM变换器的控制策略及其参数优化[J].东北电力大学学报，2014，34(5)：20-26.

[18] 刘金琨.滑模变结构控制MATLAB仿真[M].北京：清华大学出版社，2005：141-143.

Maximum Power Point Tracking of Large Scale Variable Speed Wind Turbine Based on Sliding Mode Control

Zeng Lingquan，Wang Meiqi，Zhang Jiaqi，Feng Tianshu

(Electrical Engineering College，Northeast Electric Power University，Jilin Jilin 132012)

To solve the problem that the maximum wind energy capture based wind energy utilization rate decreases due to the error in parameter identification of wind turbine or wind speed fluctuation，According to the known characteristics of wind turbines and variable structure control theory，under the condition of below rated wind speed，put forward a nonlinear feedback control scheme for variable speed wind turbines without wind speed measurements.The best torque method of the maximum wind energy capture are proposed for better performance，using sliding mode controller with wind speed estimation，making use of the rotate speed value for maximum power tracking，and there is no need for wind speed measured or estimated.Finally，the system model was built and simulation results were compared with those of the known method，which showed the correctness and effectiveness of the proposed control strategy.

Sliding mode control；Variable speed wind generator；Maximum power point tracking；Nonlinear control

2016-10-28

曾令全(1964-)，男，教授，主要研究方向:新能源发电及电力系统电能质量的分析与控制.

1005-2992(2017)02-0031-08

TM614

A

电子邮箱： 394407408@qq.com(曾令全)；wangmeiqimq@163.com(王美琪)；735969179@qq.com(张佳琦)；738832890@qq.com(冯天舒)