励磁调差系数对改善系统暂态电压稳定性的作用
李晓明,黄大为,张鹏宇
(1.国网天津武清供电有限公司,天津 301700;2.东北电力大学 电气工程学院,吉林 吉林 132012;国网吉林省电力有限公司,吉林 长春 130000)
励磁调差系数对改善系统暂态电压稳定性的作用
李晓明1,黄大为2,张鹏宇3
(1.国网天津武清供电有限公司,天津 301700;2.东北电力大学 电气工程学院,吉林 吉林 132012;国网吉林省电力有限公司,吉林 长春 130000)
针对电力系统动态无功支撑能力不足导致的暂态电压稳定问题,研究了发电机励磁调差系数优化对改善机组动态无功响应,提高系统暂态电压稳定性的作用。首先介绍了励磁调差系数的概念,然后分析了调差系数设置对机组自身稳定性的影响,并提出了调差系数的建议调整范围。对广东电网典型方式的算例分析结果表明,广东电网内的发电机组励磁调差系数优化后,能够有效提高故障后系统电压的恢复能力。
励磁系统;调差系数;暂态电压稳定;动态无功
发电机作为电力系统重要的动态无功电源,在系统故障电压跌落的情况下能够快速输出动态无功,为系统受端电压跌落提供动态支撑。发电机的无功功率是由励磁系统控制,因此,励磁系统的控制参数对机组的无功功率控制至关重要。
励磁系统调差系数是描述同步发电机无功电压外特性的参数,其值大小不但对发电机电压和无功功率具有重要影响,也间接影响到电网电压水平[1-3]。为了改善系统的电压水平,有必要对励磁系统调差系数进行合理整定。
根据发电机励磁系统技术要求的国家标准,励磁系统应保证同步发电机无功电流补偿率(无功电流调差率)的整定范围不小于±15%[4-6]。对发电机励磁系统调差系数的整定以保证发电厂内发电机安全运行且
并列运行的发电机间无功功率合理分配为目标,并未考虑发电机励磁系统调差系数对电网电压的支撑作用[7-8]。目前国内的省级电力公司大多未将发电机励磁调差系数纳入管理,以广东为例,省内的发电机励磁系统调差系数整定值基本采用出厂默认设定,并未充分发挥发电机的无功调节能力。
无功补偿容量不足和配备不合理是我国电网建设和运行中长期存在的问题,特别是可调节的无功容量不足,快速响应的无功调节设备更少[9-10]。发电机是系统最大的无功源,如何通过优化内部励磁参数,改善故障情况下机组的动态无功特性,尽可能地为系统提供动态无功支撑,对提高系统暂态电压稳定性有重要的意义。
本文深入分析了励磁调差系数对改善系统暂态电压稳定性的作用,通过全面的仿真分析,研究调差系数的调整范围,提出广东电网励磁参数优化推荐方案,并分析了推荐方案对系统安全稳定的影响。仿真分析结果证明了本文所提策略的有效性。
1 励磁调差系数
为使并列运行的各发电机组按其容量向系统提供无功功率,实现无功功率在各机组间稳定合理的分配,在励磁控制器中,一般都设有改变发电机电压调节特性斜率的环节,即调差系数。
调差系数δ是用来表征发电机电压调节特性(Uf=f(IQ),IQ:无功电流)曲线的斜率。调差系数的物理意义为同步发电机在功率因数等于零的情况下,无功电流从零变化到额定值时,发电机端电压变化的标么值。它通常用下式表示:

图1 调差特性曲线
(1)
式中:ΔU/UN为电压变化相对值;ΔIQ/IN为无功电流变化相对值。
习惯上规定,向下倾斜的特性曲线(即电压随无功负荷增加而下降)的调差系数为正,称为正调差,这可以理解为:当无功电流增大时,自动励磁控制器感受到的电压上升(虚假上升),于是控制器降低励磁电流,驱使发电机电压下降;反之,向上倾斜的特性曲线的调差系数为负,称为负调差,可以理解为:当无功电流增大时,自动励磁控制器感受到的电压下降(虚假下降),于是控制器增大励磁电流,驱使发电机电压上升。特性曲线,如图1所示。实际应用中,由于无功电流不易测量,所以通常直接用无功功率代替无功电流。
发电机电压调节器都设有调差装置,就是在电压测量回路中取机端电压Vt与定子电流在电抗上的压降的相量和的绝对值作为控制信号。
调差系数在北美也被称为无功电流补偿(Reactive Current Compensation-RCC),其中定子电流换成无功电流,如果两台机在机端直接并联,为使无功功率能在两台机之间稳定分配,电流信号取正,则测量所得的控制信号Vc,总是比实际机端电压要高,在稳态的情况下,信号电压要与参考电压Vref平衡(接近相等),则机端电压就一定要比参考电压Vref要低,例如Vref=1.0,则机端电压一定低于1.0,且定子电流越大,电压越低,即电压外特性是下斜的,北美称之为下斜特性(Droop),我国称之为正调差。如果定子电流取负号,则机端电压随着定子电流的增大是上升的,即电压外特性是上升的,我国称之为负调差,北美称之为线路电压降补偿(LineDroopCompensation-LDC)。
采用负调差,补偿部分升压变的电抗对改善系统电压控制是有明显作用的,而且不需新增任何投资,但是过去并没有得到普遍应用,原因是对于负调差对系统电压的控制及系统稳定性的作用认识及经验不足,图2所示的系统来比较并联电容及发电机对系统无功功率补偿方面的不同特性。
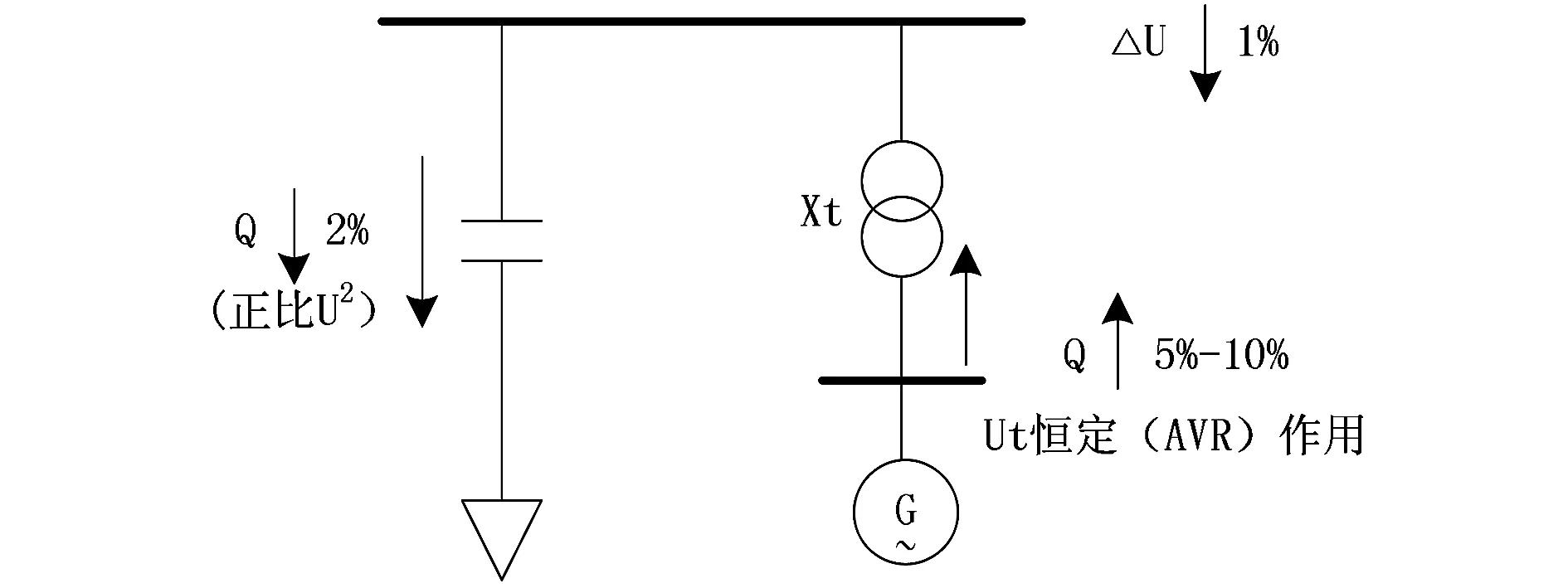
图2 无功功率补偿的不同特征

2 调差系数设置及限制条件
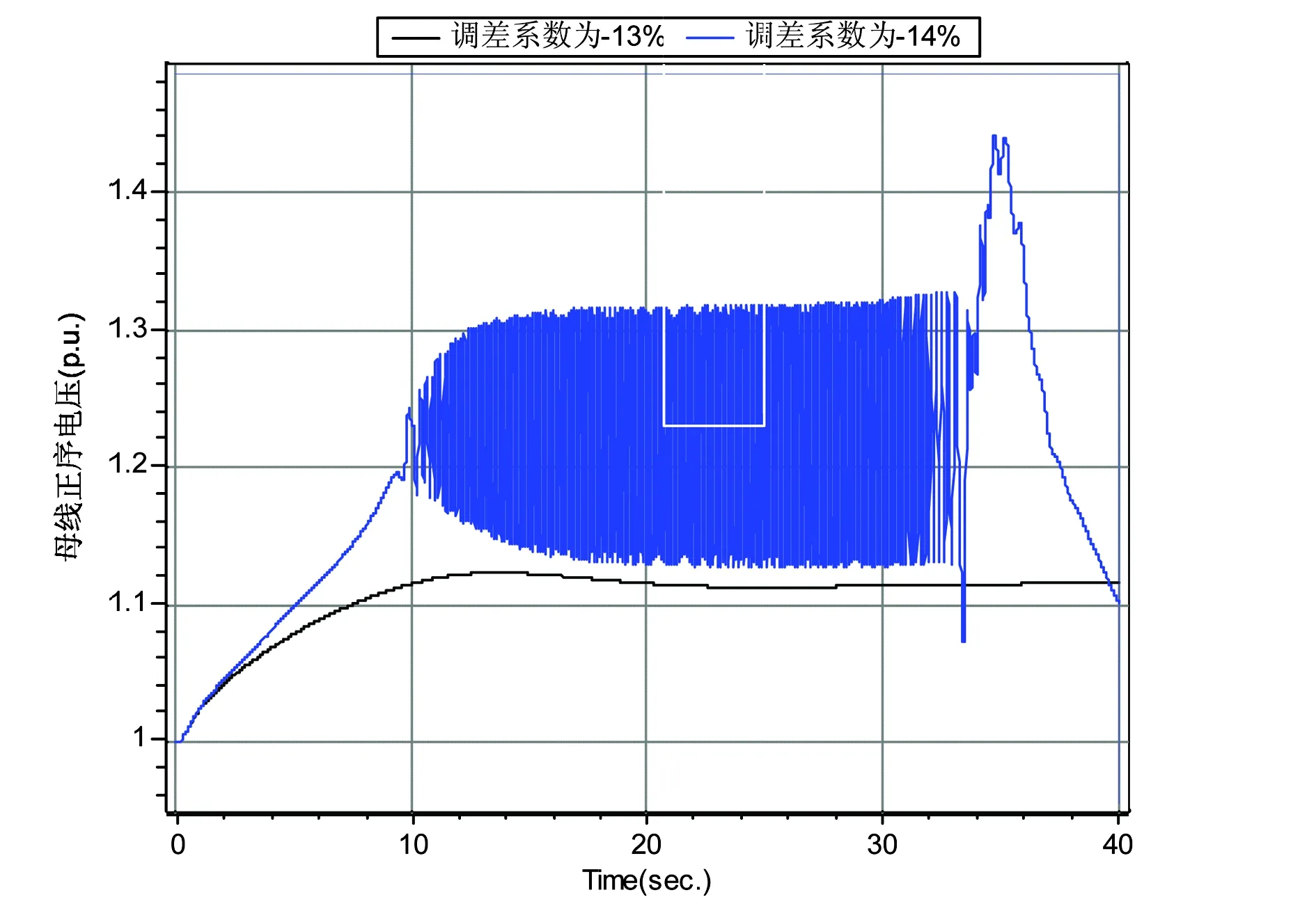
图3 广东某电厂#1机负载2%阶跃,机端母线电压
调差系数δ是表征机组无功调节特性的物理量。机组无功输出是由励磁系统提供和调节的,改变励磁调差系数会相应的改变机组端电压和无功输出,其中无功变化较大,因此对励磁调差系数进行设置时,应充分考虑机端电压和机组无功输出的安全范围,避免越限。在一个复杂电力系统中如何确定发电机的负荷补偿系数一直没有提出有效的设计方法,在实际电力系统运行中也没有指导负荷补偿系数的确定依据[11]。在国外成功应用的先例中也是大致地限定在某较合理的补偿范围内[12-13]。有文献报道[14],美国西部电力系统中波特莱区的负荷,由于向它送电的9个发电厂采用负调差补偿了50%升压变电抗,在一次故障后避免了电压崩溃,其效果等同装置460 MVA、500 kV的可切换电容器。
一般文献建议补偿升压变电抗的50%~80%,ABB推荐一机一主变组成的发电单元的总阻抗在3%~8%比较合适,即“调差+主变电抗”的值在3%~8%之间。
图3是广东某电厂#1机(机组容量600 MW)负载2%阶跃时的仿真结果,由图可见,当机组调差系数设置为-14%时,阶跃扰动下机组将不能维持稳定运行,因此该机组调差系数不宜超过-13%。
广东电网机组升压变的漏抗基本在13%~15%区间范围内,为研究调差系数设置的最大可调范围,对不同机组进行仿真分析。大量仿真计算的结果表明,负调差对机组升压变阻抗的补偿度过高会降低机组自身稳定特性,为保证稳定性,建议广东机组的调差补偿度不超过70%。
3 调差系数对系统暂态电压稳定的影响
采用广东电网2013年某典型方式数据,50%电动机+50%恒阻抗负荷模型,故障类型为北郊站三相短路500 kV单相中开关拒动,调整广东地区的发电机励磁调差系数,调节范围从0~-10%,计算调差系数对系统电压恢复能力的提升效果。北郊站三相短路单相中开关拒动故障下鹿鸣站母线正序电压如图4所示,仿真结果表明,广东电网全网机组调差系数对故障后母线电压恢复时间有明显的作用,母线电压的恢复时间随着调差系数的绝对值增大而缩短。

图4 北郊站三相短路单相中开关拒动故障下鹿鸣站母线正序电压
2013年某典型方式下,考虑广东电网采用50%感应电动机+50%恒阻抗负荷模型时,按补偿机组升压变漏抗70%的原则,调整机组的调差系数,通过仿真计算,分析机组调差系数对存在暂态电压失稳问题的站点电压恢复的影响,仿真结果如图5和图6所示。

表1 广东电网机组调差系数对电压恢复影响

图5 莞城站三永中开关拒动故障下大朗站母线正序电压图6 北郊站三相短路单相中开关拒动故障下鹿鸣站母线正序电压
2013年某典型方式下,考虑广东电网采用50%感应电动机+50%恒阻抗负荷模型时,莞城、北郊站点发生三相短路单相中开关拒动故障下广东电网存在暂态电压失稳问题:
(1)莞城-宝安线路莞城侧三相短路单相中开关拒动会导致大朗站存在暂态电压失稳问题,广东电网机组调差系数优化设置前,大朗等站点电压低于0.75 pu的持续时间为102周波,在250周波时达到稳态值;广东电网机组调差系数优化设置后,大朗等站点电压低于0.75 pu的持续时间缩短为81周波,在150周波时达到稳态值,缩短100周波。
(2)北郊-花都线路北郊侧三相短路单相中开关拒动会导致鹿鸣站存在暂态电压失稳问题,广东电网机组调差系数优化设置前,鹿鸣等站点电压低于0.75 pu的持续时间为105周波,在400周波时达到稳态值;广东电网机组调差系数优化设置后,鹿鸣等站点电压低于0.75 pu的持续时间缩短为82周波,在175周波时达到稳态值,缩短225周波。
4 结 论
负调差对升压变的补偿度越大,机组的动态无功输出能力越强,对系统电压恢复的支撑效果越好;但补偿度过大会影响机组的自身的稳定和厂内机组间的无功分配,因此,补偿度不宜超过70%。对全网机组的励磁调差系数进行优化,研究负调差对电网电压的支撑效果。仿真结果表明:广东电网机组的调差系数优化后,对系统的电压支撑效果明显。
[1] 邱军,梁才浩.电厂的电压无功控制策略和实现方式[J].电力系统及其自动化学报,2004,16(2):69-72.
[2] 李志恒,付红军,孙建华,等.电厂侧自动电压控制系统电压控制策略的改进[J].电力系统自动化,2011,35(9):96-99.
[3] J.B.Davies,L.E.Midford.High side voltage control at manitoba hydro [C].Proceedings of 2000 IEEE Power Engineering Society Summer Meeting:16-20 July,2000,Seattle,Washington,USA.
[4] 中国电器工业协会,全国旋转电机标委会发电机分技术委员会.同步电机励磁系统大、中型同步发电机励磁系统技术要求[S].北京:中国标准出版社,GB/T 7409.3—2007.
[5] 刘迎迎,孙毅,李昕,等.电力系统电压稳定方法综述[J].东北电力大学学报,2013,33(5):43-47.
[6] 郑琳,田晨阳.电力系统电压稳定机理探究[J].东北电力大学学报,2015,35(4):1-3.
[7] 安军,穆钢,郑太一,等.改善电网电压水平的发电机励磁系统调差系数优化策略[J].电力系统自动化,2013,37(23):97-101.
[8] 王明星,穆钢,安军,等.电力系统多时段多目标的发电机励磁系统调差系数优化整定[J].电网技术,2013,37(11):3178-3183.
[9] 任丕德,刘发友,周胜军.动态无功补偿技术的应用现状[J].电网技术,2004,28(23):81-83.
[10] 曾艳,徐柏榆,陈晓科.广东电网电压无功运行管理现状分析及建议[J].广东电力,2010,23(11):50-55.
[11] 孙元章,贾宇,程林,等.发电机励磁控制中负荷补偿系数的优化[J].中国电机工程学报,2006,26(23):20-24.
[12] 刘取.电力系统稳定性及发电机励磁控制[M].北京:中国电力出版社,2007.
[13] Dmitry Kosterev.Design installation and initial operating experience with line drop compensation at john day powerhouse[J].IEEE Transaction on Power System,2001,16(2):261-265.
[14] C.W.Taylor.Line drop compensation,high side voltage,secondary voltage control-why not control a generator like a static VAr compensator[C].Proceeding of IEEE Power Engineering Society Summer Meeting:16-20 July,2000,Seattle,Washington,USA.
The Effect of Difference Coefficient of Generator Excitation System on Power System Transient Voltage Stability
Li Xiaoming1,Huang Dawei2,Zhang Pengyu3
(1.State Grid Tianjin Wuqing Power Supply Co.,ltd.,Wuqing Tianjin,301700;2.Electrical Engineering College,Northeast Electric Power University,Jilin Jilin 132012;3.State Grid Jilin Electric Power Co.,ltd.,Changchun Jilin,130000)
Lack of dynamic reactive power compensation result in power system transient voltage instability.To improve the transient voltage stability,this paper presents an optimization strategy for setting the excitation system difference coefficient of the generator.The concept of the excitation system difference coefficient is introduced.Then the impacts of difference coefficients of generator excitation system on generator stability are analyzed and adjustment range is proposed.The calculation results of Guangdong province system show that the transient voltage stability level is enhanced effectively after optimize the excitation system difference coefficient.
Generator excitation system;Difference coefficient;Transient voltage stability;Dynamic reactive power
2016-07-23
国家自然科学基金(51307019);吉林省科技支撑项目(20140101210JC)
李晓明(1989-),男,硕士,助理工程师,主要研究方向:电力系统稳定运行与控制.
1005-2992(2017)02-0009-05
TP29
A
电子邮箱: 18692656020@163.com(李晓明);hdw76@163.com(黄大为);89705999@qq.com(张鹏宇)

