滨海湿地稀疏采样重构高光谱图像分类精度评价

孙钦佩，马 毅,张 杰*

（1.山东科技大学，山东 青岛 266590；2.国家海洋局第一海洋研究所，山东 青岛 266061）

滨海湿地稀疏采样重构高光谱图像分类精度评价

孙钦佩1,2，马 毅1,2,张 杰1,2*

（1.山东科技大学，山东 青岛 266590；2.国家海洋局第一海洋研究所，山东 青岛 266061）

高光谱遥感影像维数高、数据量大、波段之间的相关性强，分类时易出现"Hughes"现象，因此在分类过程中如何有效减小数据处理过程中的计算量，又保证原始数据重要的地物信息不丢失具有重要的意义。压缩感知理论可通过远低于耐奎斯特的采样率和少量观测数据实现信号的精确重构，具有对硬件读写要求低、图像恢复效果好等优势。通过利用基于小波变换的压缩感知算法对黄河口地区的高光谱影像进行图像重构，然后分别采用SVM算法、最大似然法以及神经网络分类法对重构后的影像进行分类，并对分类结果的精度分别从空域和小波域、不同的测量值等维度进行了分析和比较。结果表明：（1）压缩感知理论重构后的影像保留了原始影像的基本信息，保证了分类精度；（2）SVM算法的分类精度最好，空域和小波域的分类精度基本一致；（3）分类精度随测量值的增加先逐渐提高，然后趋于稳定。

高光谱影像；稀疏采样；压缩感知；图像分类

滨海湿地是陆地生态系统和海洋生态系统的交错过渡地带，主要包括滩涂湿地、浅海湿地、岛屿湿地等。滨海湿地拥有众多野生动植物资源，并且具有强大的生态净化作用，是重要的生态系统，因此对湿地及湿地中的丰富物种的研究及保护具有重要的意义。

高光谱遥感影像将传统的图像维和光谱维信息融为一体，实现了“图谱合一”，在对目标的空间特征成像的同时，每个空间像元覆盖了几十乃至几百个窄波段连续的光谱，提供了地面单元精细的光谱特征。通过对图像和光谱数据进行处理，可以获得大量隐含的特征信息，用于地物的识别、分类等。分类是遥感影像数据处理中关键内容之一，通过分类可以获得诸多精细的高光谱信息。但是高光谱数据在提供丰富信息的同时，由于不同波段，特别是相邻长波段之间往往具有较强的相关性，导致信息冗余，对数据的存储和传输提出了更高的要求；此外，直接利用所有的波段信息进行分类时，亦有可能会使分类精度降低。如何既能有效地降低高光谱图像处理过程中的复杂度又可以保证分类的精度，对高光谱数据处理具有重要的意义。因此，有必要对图像分类后的精度进行评价。

1996 年，Olshausen[1]等指出自然图像本身存在稀疏性，并揭示了图像数据的稀疏本质，目前已经有很多学者成功地将稀疏表示理论应用到了图像分类中。Siddiqui[2]等提出稀疏主成分分析方法，将稀疏表示方法应用于高光谱图像分类；Yi Chen[3-4]等将稀疏表示用于高光谱遥感图像的分类和目标检测中，并与支持向量机（Support vector machine，SVM）等方法进行了对比分析；何同弟[5]等提出了自适应的稀疏表示方法来进行高光谱遥感图像分类；宋相法[6]等结合稀疏表示和光谱信息，利用随机森林法对高光谱遥感图像进行了分类。但由于基于规则信号进行重建缺乏泛化性能，为了克服这种局限性，杜培军[7]等提出一种通过字典重建和带有全变差的稀疏表示模型规则化的判别分类器学习方法，并取得了较好的分类效果。以上方法均利用稀疏理论产生的特征进行分类。2006年，D.Donoho和E. eandesJ.Romberg[8-10]等在稀疏理论的基础上提出了压缩感知(Compressed Sensing，CS)理论框架，将稀疏理论发展到一个新的高度[11]，到目前为止压缩感知理论已经成功应用到摄影、医学、人脸识别、地球物理和遥感等领域[12-16]。在高光谱影像分类方面，其分类算法通常分为监督分类和非监督分类，代表性的监督分类方法主要有支持向量机法、最大似然法、神经网络法和最小距离法等；非监督分类法主要有ISODATA法和K均值聚类方法等。以上这些分类方法直接对图像进行分类处理，计算量较大。压缩感知理论，以远低于耐奎斯特的采样率进行采样，通过少量观测数据即可精确重构原始信号，是一种对存储和传输要求低、图像恢复效果好的图像重构算法。通过压缩感知算法对图像进行稀疏采样重构，既可以降低图像处理的复杂度，又保留了图像的基本信息，对高光谱数据处理具有重要的意义。

本文通过对一景地物类型丰富的滨海湿地PROBA CHRIS高光谱遥感图像进行处理，采用基于小波变换的压缩感知算法进行图像重构，然后分别利用SVM法、最大似然法以及神经网络分类方法对重构后的影像进行分类，并对分类后的结果精度分别从空域和小波域、不同的测量值等维度进行了分析和比较。

1 数据与方法

1.1 数据

（1）CHRIS影像黄河口数据。 CHRIS是ESA搭载于小卫星PROBA上的传感器，全称为紧凑式高分辨率成像光谱仪，具有5种成像模式（见表1），可获取0°，+36°，-36°，+55°和-55°等5种角度的高光谱图像。本文应用的实验数据选自2012年6月CHRIS利用工作模式2获取的黄河口滨海湿地的0°图像（图1），其光谱范围为406～1 035 nm，光谱分辨率为1.25～11.00 nm，地面分辨率17 m。CHRIS图像覆盖的区域位于黄河入海口新老河道交界处。该区域湿地地物丰富，包含有天然湿地和人工湿地，其中包括芦苇、翅碱蓬、柽柳和滩涂等天然湿地和养殖水面、水库等人工湿地。

图1 研究区影像示意图

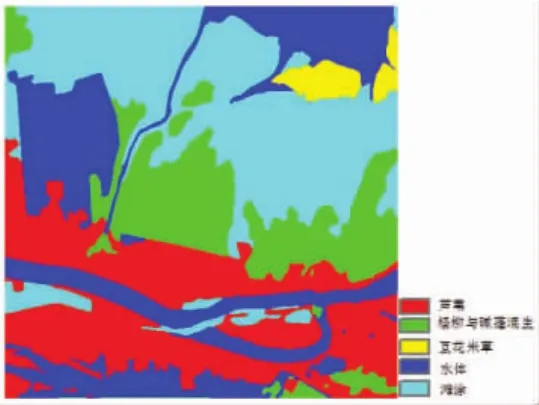
图2 实验验证数据

表1 CHRIS卫星遥感影像详细参数

（2）验证数据。 实验所采用的验证数据是根据所获取的影像数据和现场踏勘的资料，然后经人工解译而成。研究区域总共划分为5个类别，其中深蓝色区域表示水体，浅蓝色区域表示滩涂与裸地，红色区域表示芦苇，绿色区域表示碱蓬柽柳混生，黄色区域表示互花米草，如图2所示。

1.2 方法

1.2.1 压缩感知算法 经典的香农采样定理认为，为了不失真地恢复模拟信号，采样频率应不小于模拟信号频谱中高频率的2倍，因此，数据中存在较大程度冗余。Donoho[8]等提出的压缩感知方法充分运用了大部分信号可以稀疏表示这一先验信息，利用随机投影在远低于奈奎斯特频率的采样频率下，对压缩数据进行了直接采集，突破了香农采样定理的瓶颈，使得在第一频域内高分辨率信号的采集成为可能。压缩感知理论指出，如果信号在某一变换域内是k稀疏的，那么可以设计一个与表达基不相关的非满秩矩阵（测量矩阵）来对信号进行测量，该测量值的长度远小于原始信号的长度，然后利用测量值，通过求解一个凸最优化问题来实现原始信号的重构。常用的稀疏基有正交基、正弦基、余弦基、傅里叶基以及小波基等，本文采用的是小波基。

假设图X可用小波基Ψ=[Ψ1,Ψ2…,Ψm]的线性组合表示，即：

当图像X在小波基ψ上仅有k＜＜n个非零系数αk时，称ψ为X的表达基。将图像X通过Hadamard测量矩阵Φ[φ1,φ2,…，φm]投影到Y，即：

将式（1）代入式（2），则有：

由于α是k稀疏的，且k＜＜n，则可以利用稀疏分解算法，在表达基ψ和测量矩阵Φ不相关的情形下，通过式（3）就可求解得到稀疏系数α。利用小波压缩感知进行图像重构的过程包括：通过测量矩阵Φ计算测量投影值Y，应用式（3）求解稀疏系数α，将稀疏系数α代入式（1）就可重构图像X¯。

1.2.2 遥感图像分类算法 常见的高光谱分类方法主要有SVM法、最大似然法、决策树方法、神经网络法和最小距离法等。本文主要采用SVM法、最大似然法、以及神经网络分类法对图像进行分类。

（1）支持向量机法(SVM)。支持向量机(Support Vector Machine,SVM)是针对两类问题的判别分类器，以结构风险最小化为基础(Vapnik,1998)，其目的是在特征空间中寻找拥有最大分类间隔的线性判别准则[17]。通过使用一个非线性映射p，将样本空间映射到一个高维特征空间中使其线性可分。在特征空间中建构最优分割超平面，转化为一个凸二次规划问题的求解，使其间隔最大化，使得学习器得到全局最优化。SVM作为一种最新的也是最有效的统计学习方法，因其适用高维特征以及小样本不确定性问题，是一种极具潜力的高光谱分类方法[18]。

（2）最大似然法（MLC）。最大似然分类法根据最大似然比贝叶斯判决准则法，采用统计方法对感兴趣区域进行计算，建立非线性判别函数集，假设分布函数为正态分布。将待分类图像中的每个像元代入各个类别的分类函数，将函数返回值最大的类别作为该像元的归属类别，从而达到分类的效果。

在遥感影像的分类中，最大似然法假设影像多波段数据的分布为多维正态分布，以此来构造判别分类函数。其基本思想是：每一个波段的每一类像元数据均形成一个正态分布，因此该类多波段数据便构成自身的一个多维正态分布，不同种类训练样本构造出各类的多维正态分布模型，即概率密度函数或概率分布函数，对于未知类别的数据向量，通过贝叶斯公式计算其属于各个类别的概率大小，根据概率的大小对像元进行分类。

（3）神经网络法。神经网络是一种模仿动物神经网络行为特征进行分布式并行信息处理的数学模型，通过模拟动物神经元的行为和神经系统的组织结构，构建仿真网络系统，借助于调整内部大量节点之间相互连接的关系，从而达到信息处理的目的。神经网络的基本单元是神经元，把多个神经元按一定的层次结构连接起来，便可得到神经网络。神经网络的学习过程，本质上是根据训练数据来调整神经元之间的连接权值以及每个功能神经元的阈值。

1.2.3 对比试验设计 (1)将测量值设置为200，测量在空域执行，将重构后图像分别采用SVM方法、最大似然法以及神经分类的方法，结果与参考样方进行视觉分析和定量分析。分别从总体分类精度、Kappa系数等方面进行比较分析；(2)将采样数分别设置为300，400，500，600和700，然后按以上几方面进行比较；(3)测量在小波域执行，实验操作同上；然后将在空域执行和小波域执行的3种方法分类结果分别进行比较。

2 结果与分析

从图3可见，随着测量值M的增加，重构后的影像越来越清晰，当M值取600时，重构后的影像基本与原始影像一致。未经压缩的原始影像分别采用SVM方法、最大似然法以及神经法分类后的结果如图4所示，其中采用SVM分类方法的总体精度为83.07%，Kappa系数为0.78；最大似然法分类的总体精度为81.84%，Kappa系数为0.76；神经网络法分类的总体精度为 79.36%，Kappa系数为0.73。

图3 不同测量值重构影像

图4 原始影像不同算法分类结果

表2 不同测量值下3种算法分别在空域和小波域分类结果总体精度

2.1 不同分类算法的分类精度比较与分析

当测量值M取200的时，分别采用上述3种方法在空域上进行分类后的结果如图5所示；显然，与原始影像分类结果相比，测量值为200时的分类结果有较多混合斑块，部分地物没有明显的区分出来。此时SVM分类方法的总体精度为79.80%，Kappa系数为0.73；最大似然法分类的总体精度为76.82%，Kappa系数为0.70；神经网络法分类的总体精度为76.27%，Kappa系数为0.69。改变测量值M的取值，同时在空域和小波域执行后的结果分别如图6所示。

图5 测量值M=200时不同算法分类结果

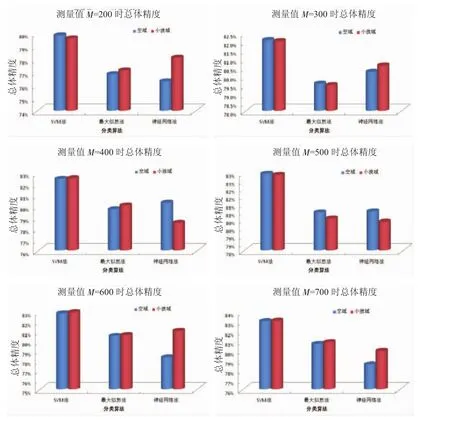
图6 不同算法分类精度

从图6可见，3种分类方法中，无论测量值M取值为多少，SVM法分类效果最佳，总体精度最高，最大似然法次之。其中，SVM法和最大似然法在空域和小波域的执行结果基本一致，而神经网络方法的精度在空域和小波域的精度相差起伏较大。

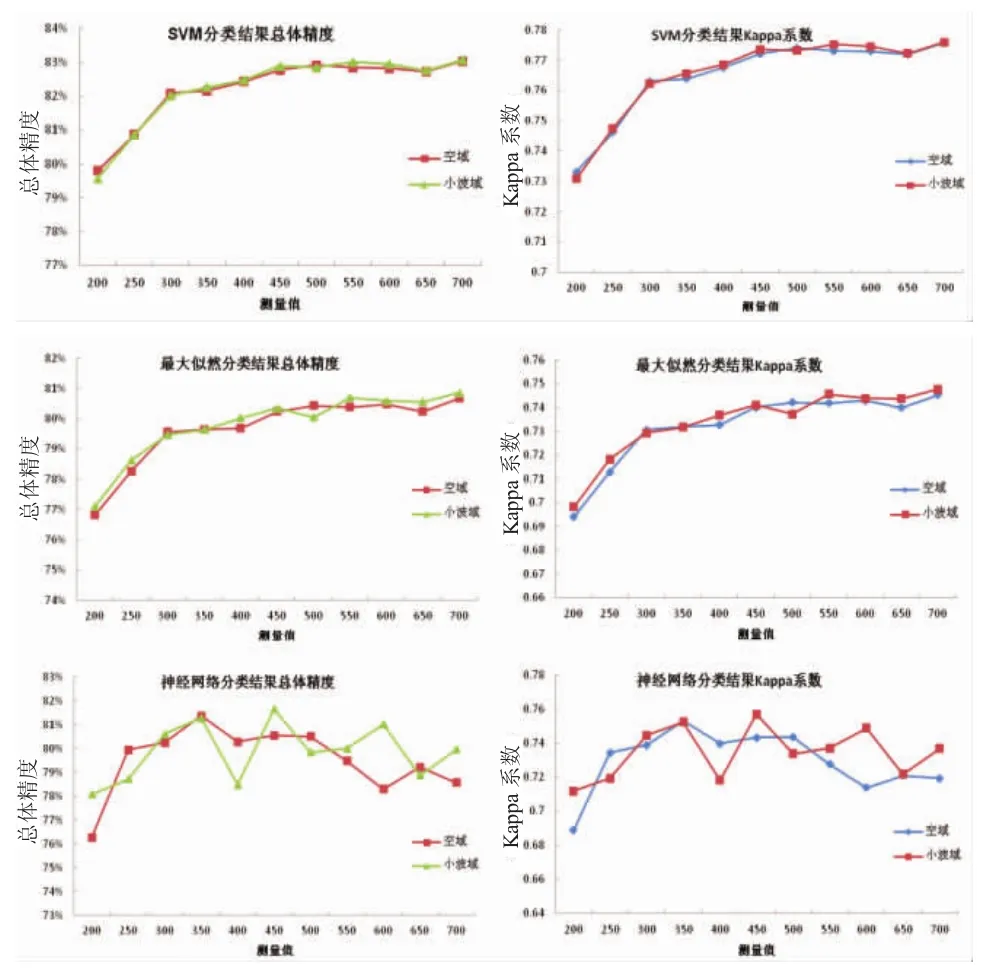
图7 不同测量值的分类精度

2.2 不同测量值的分类精度比较与分析

从图7可见，当测量值取值较小时，3种方法分类结果的总体精度较低，随着测量值的增加，SVM方法以及最大似然法的分类精度也随之增加；虽然空域和小波域的执行结果相差较小，但小波域的分类精度相对较高，其中SVM方法在小波域比空域的平均分类精度提高约0.02%，最大似然法在小波域比空域的平均分类精度提高约0.14%。神经网络法的分类精度随测量值的变化较大，但同样在小波域的分类精度较高，其平均精度比在空域的精度提高约0.35%，当测量值M取值350时，其分类精度约81.37%，相对于未经压缩的原始影像的分类结果，精度提高约2%。

2.3 不同执行域的分类精度比较与分析

从图8可见，SVM方法在小波域和空域的分类精度均为最高；最大似然法的精度变化趋势与SVM法一致，随着测量值M的增加，分类精度呈增长趋势，但当测量值增加到500时，两种方法的分类精度达到一个峰值（其中，SVM方法在空域分类精度为 82.92%，与原始影像的分类精度相差0.16%），此后，分类精度基本呈平稳趋势，而当测量值取700时，分类精度再次达到一个峰值，SVM方法在小波域的分类精度达到83.07%，比原始影像的分类精度降低约0.0065%，最大似然法在小波域的分类精度为80.86%，比原始影像的分类精度降低约0.98%。神经网络方法的分类精度变化起伏较大，其精度最高时为当测量值取350时在空域分类结果，精度为81.37%，相对于原始影像分类精度，提高约2%；当测量值为450时，小波域的分类结果的分类精度为81.65%，相对于原始影像分类结果，提高约2.3%。

图8 不同执行域的分类精度

3 结论与讨论

本文通过采用基于小波变换的压缩感知算法对黄河口地区的高光谱影像进行了图像重构，然后分别利用SVM法、最大似然法以及神经网络分类方法对重构后的影像进行分类，并对分类后的结果精度分别从空域和小波域、不同的测量值等维度进行了分析和比较。得出以下结论：

（1）重构后的影像保留了原始影像的基本信息，保证了分类精度；

（2）无论是在空域还是小波域，SVM法的分类精度均为最佳，最大似然法次之，且算法相对稳定；

（3）空域和小波域的执行结果基本一致，故可认为执行域对重构的结果影响微小；

（4）SVM法和最大似然法分类精度均随测量值的增加，先逐渐提高，然后趋于稳定，而神经网络法分类精度随观测值变化起伏较大。

总体概括来说，压缩重构后的高光谱影像既减少了处理过程中的复杂度，又保证了分类精度，这对高光谱影像的处理和研究具有重要的意义。

由于测量矩阵选取测量值时具有一定随机性，实验中，同一测量值重构后的影像分类精度略有不同，但对整体结果影响较小。如何选择最佳观测值，使得分类精度最高仍需进一步探讨。

[1]Olshausen B A,Field D J.Emergence ofsimple-cell receptive field properties by learning a sparse code for natural images[J].Nature, 1996,381(6583):607-609.

[2]Siddiqui S,Robila S,Peng J,et al.C for Hyperspectral Data Classification[C]//IEEE International Geoscience&Remote Sensing Symposium,IGARSS2008,July8-11,2008,Boston,Massachusetts,USA,Proceedings.2008:577-580.

[3]Chen Y,Nasrabadi N M,Tran T D.Sparse representation for target detection in hyperspectral[J].IEEE Journal of Selected Topics in Signal Processing,2011,5(3):629-640.

[4]Chen Y,Nasrabadi N M,Tran T D.Classification for hyperspectral imagery based on sparse representation[C]//The Workshop on Hyperspectral Image&Signal Processing:Evolution in Remote Sensing.2010:1-4.

[5]何同弟,李见为.基于自适应稀疏表示的高光谱遥感图像分类[J].系统工程与电子技术,2013,5(9):1994－1998.

[6]宋相法,焦李成.基于稀疏表示及光谱信息的高光谱遥感图像分类[J].电子与信息学报,2011,34(2):268－272.

[7]Du P,Xue Z,Li J,et al.Learning discriminative sparse representations for hyperspectral image classification[J].IEEE Journal of Selected Topics in Signal Processing,2015,9(6):1-1.

[8]E.Candès,J.Romberg and T.Tao.Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information.IEEE Transactions on Information Theory,2006,52(2):489-509.

[9]E Candès，T Tao.Near optimal signal recovery from random projections:Universal encoding strategies?[J].IEEE Transactions on Information Theory,2006,52(12):5406-5425.

[10]DDonoho.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.

[11]李树涛,等.压缩传感综述[J].自动化学报,2009,35(11):1369-1377.

[12]Duarte MF,et a1.Single pixel imaging via compressive sampling[building simpler，smaller，and less-expensive digital cameras][J]. IEEE Signal ProcessingMagazine,2008,25(2):83-91.

[13]LustigM,et a1.Compressed sensingMRI[J].IEEE Signal ProcessingMagazine,2008,25(2):72-82.

[14]Wright J,et a1.Robust face recognition via sparse representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009,31(2):210-227.

[15]Hennenfent G,Herrmann F J.Simply denoise:wavefield reconstruction via jittered undersampling[J].Geophysics,2008,73(3): 19-28.

[16]Baraniuk R Steeghs P C.Compressive radar imaging.[C]//2007 IEEE Radar Conference,Boston,128-133.

[17]Vapnik VN．Statistical LearningTheory[M].NewYork：Wiley,1998

[18]杜培军,林卉,孙敦新.基于支持向量机的高光谱遥感分类进展[J].测绘通报,2006(12):37-40.

Evaluation of the Classification Accuracy of Coastal Wetland Hyperspectral Image Reconstructed from Sparse Sampling

SUN Qin-pei1,2,MA Yi1,2,ZHANG Jie1,2
1.Shandong University of Science and Technology,Qingdao 266590,Shandong Province,China; 2.First Institute of Oceanography,State Oceanic Administration,Qingdao 266061,Shandong Province,China

As is known to all that the hyperspectral remote sensing images have the characteristics of high dimensionality,data volume,as well as strong correlation between bands,so it tends to appear the"Hughes" phenomenon in the process of classification.Therefore,it is of great significance to effectively reduce the data processing computation in the process of classification while keeping the important feature information of the original data.The compressed sensing theory,well known as its low sampling rate,presents sampling at a rate much lower than the Nyquist sampling rate,and the signals can be accurately reconstructed with a small amount of observation data.It is a kind of image reconstruction algorithm with low requirements for storage and transmission and better effect on image restoration.In this paper,the hyperspectral image of the Yellow River Estuary Area is reconstructed based on the Wavelet transform compression algorithm,and then the reconstructed image is classified by the methods of support vector machine (SVM),maximum likelihood and neural network. Finally,the classification results are compared and analyzed by different dimensions,including the airspace and wavelet domain,as well as different measured values.Results show that the reconstructed image has kept the basic information of the original image,ensuring the classification accuracy;the SVM algorithm has the best classification accuracy which is essentially the same in the airspace and wavelet domain;the accuracy firstly increases and then remains stable with the increase of measured value.

hyperspectral image;sparse sampling;compressed sensing;image classification

P237

A

1003-2029（2017）02-0077-06

10.3969/j.issn.1003-2029.2017.02.013

2016-09-07

GF海岸带遥感监测与应用示范资助项目

孙钦佩（1991-），女，硕士研究生，主要从事遥感图像处理研究。E-mail：sunqinpei163@163.com

张杰（1963-），男，研究员，主要从事海洋遥感与信息系统研究。E-mail：zhangjie@fio.org.cn