基于遗传算法的碟型水下滑翔机结构优化

甄春博，刘兆瑞，王天霖，英 扬，于鹏垚

（1.大连海事大学 交通运输装备与海洋工程学院，辽宁 大连 116026；2.大连理工大学 运载工程与力学学部船舶工程学院，辽宁 大连 116024）

基于遗传算法的碟型水下滑翔机结构优化

甄春博1，刘兆瑞2，王天霖1，英 扬1，于鹏垚1

（1.大连海事大学 交通运输装备与海洋工程学院，辽宁 大连 116026；2.大连理工大学 运载工程与力学学部船舶工程学院，辽宁 大连 116024）

以结构质量和应力作为目标函数，结构变形为约束条件，设计碟型水下滑翔机结构优化流程，采用单参数和多参数敏感度分析方法完成关键结构参数的筛选。采用拉丁超立方试验设计方法完成了对设计空间的采样布点工作，利用样本点数据创建了滑翔机结构优化的Kriging代理模型，并对Kriging代理模型进行了联合训练，使模型的拟合达到非常高的可用精度。采用NSGA-2第二代非支配排序多目标遗传算法对滑翔机进行了结构优化求解，得到了优化的Pareto前沿面最优解。优化结果显示，结构质量和应力较优化前分别降低5.57%和14.91%，文中所提方法在滑翔机结构优化设计中具有可行性。

水下滑翔机；结构优化；敏感度分析；Kriging代理模型；非支配排序多目标遗传算法

圆碟形水下滑翔机是一种新型水下滑翔机，具有极佳的操纵性能和机动性能，在军事监测，科学研究等方面有着广泛的应用。其耐压壳结构承受工作水深压力，并为研究人员及其他设备提供安全的工作环境。同时它也是潜水器浮力的主要提供者，并且在很大程度上影响了深潜器的水动力性能[1]。因此，对耐压壳结构的优化设计显得尤为重要。

圆碟形水下滑翔机耐压壳结构的优化设计过程中，质量、应力、变形都是需要考虑的因素，是一个多目标优化设计过程。遗传算法在整个设计空间的寻优能力很强，效率良好，适应性强，较好的鲁棒性，广泛的运用于各种线性或者非线性结构，适合有约束及无约束模型[2]。基于优化思想的遗传算法具有非常灵活的延展性，面对实际工程结构中遇到的各式各样的优化问题，人们可以对遗传算法进行改进从而适应特定模型的优化，在工程结构优化领域逐渐得到广泛的应用[3-4]。在遗传算法中，NSGA-2采用简洁明晰的非优超排序机制,使算法具有逼近Pareto最优前沿的能力,采用排挤机制保证得到的Pareto最优解具有良好的散布特性，因而可获得较为理想的优化结果。

本文针对圆碟型水下滑翔机结构，采用敏感度分析方法确定优化参数，并采用代理模型及NSGA-2第二代非支配排序多目标遗传算法对滑翔机进行了结构优化分析。

1 水下滑翔机结构特点

本文水下滑翔机工作水深为100 m，外形采用水动力性能优异的流线型剖面。其结构特点如图1所示。

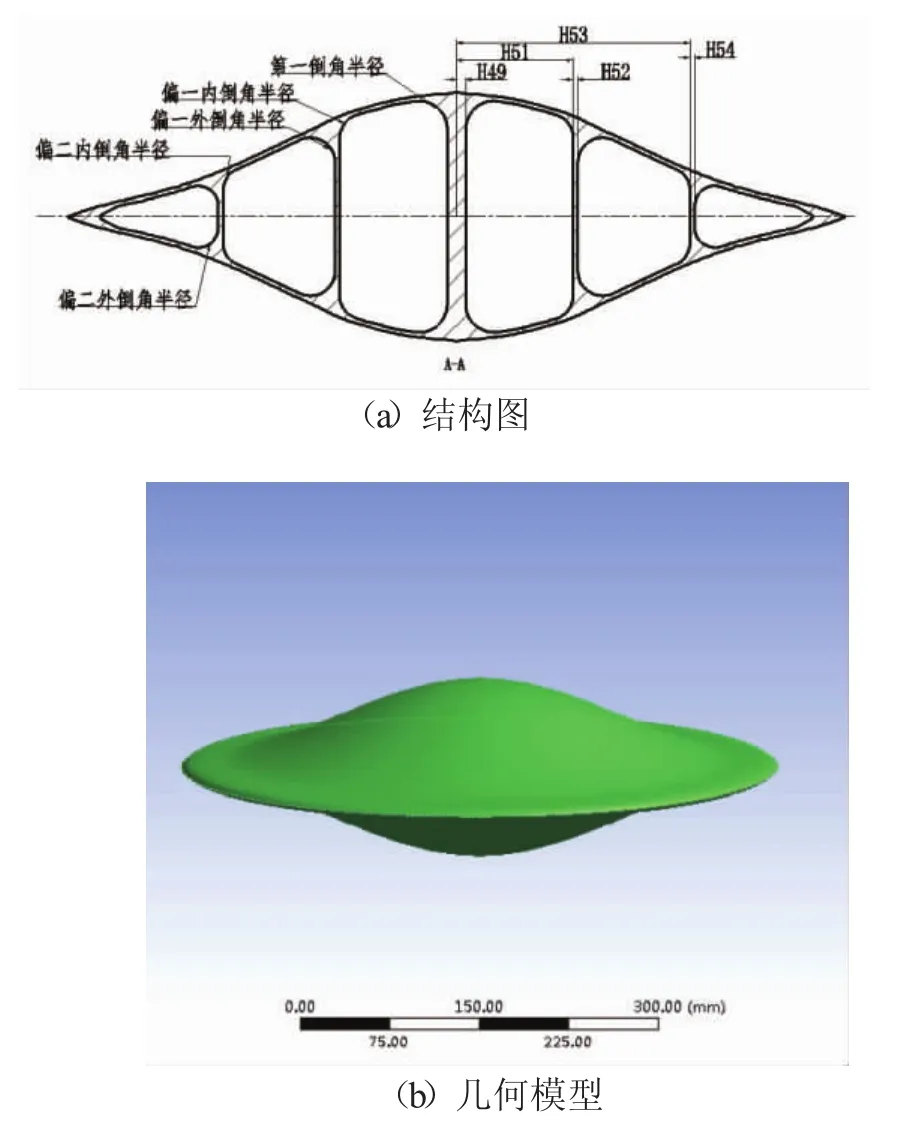
图1 滑翔机结构模型

根据有限元分析结果，选取滑翔机中心柱体半径H49，偏一圆筒内壁距离中心的距离H51，偏一圆筒的壁厚H52，偏二圆筒的内壁距离中心的距离H53，第一倒角半径（中心圆柱体倒角半径），偏一内倒角半径，偏一外倒角半径，偏二内倒角半径，偏二外倒角半径等9个主要影响结构性能的设计参数作为结构优化设计的主要参数。

2 结构优化流程

质量、应力、变形是决定滑翔机结构性能的重要指标。质量决定了滑翔机的浮力水平，影响滑翔机携带设备的多少，而且由质量引起的惯性对滑翔机的运动灵活性产生重大影响;最大等效应力决定结构的失效，影响结构的工作水深;最大变形与结构的体积相关，影响结构的浮力水平。本文以质量，应力为目标函数，结构变形为约束条件，进行结构的多目标优化设计。基本优化流程如图2所示。

图2 优化流程图

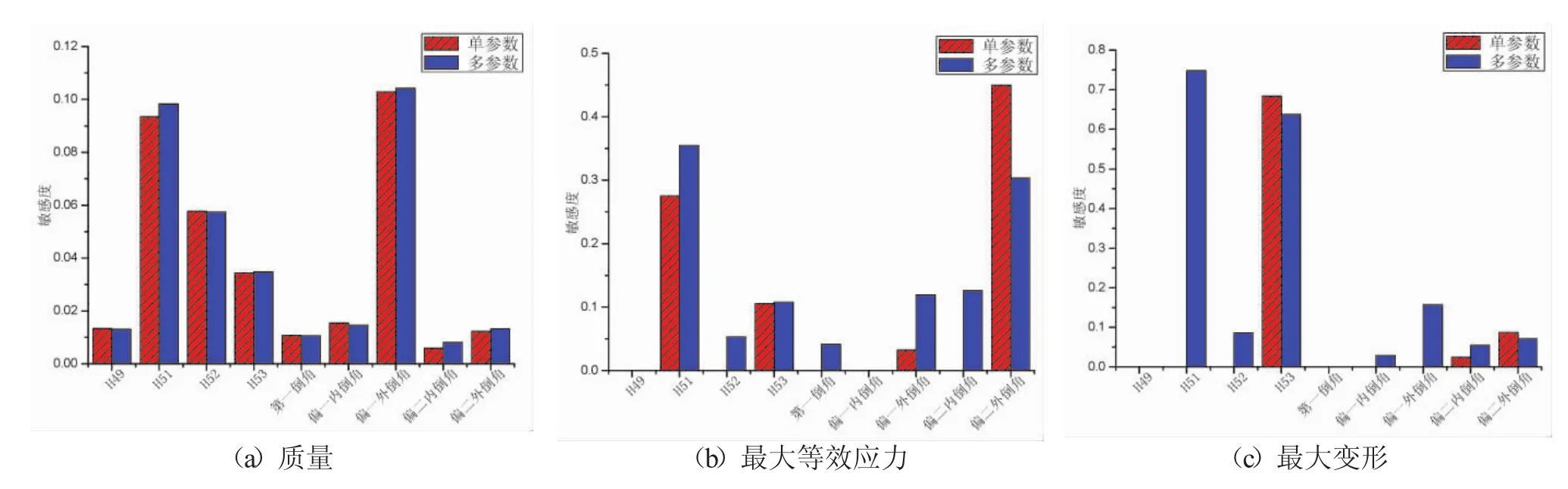
图3 结构参数敏感度结果

3 滑翔机结构参数敏感度分析

为了对水下滑翔机的结构参数进行优化设计，在优化初期应该掌握水下滑翔机的主要结构参数对其在工作时性能的影响。质量，应力，变形是决定滑翔机结构性能的重要指标，敏感性分析的主要响应参数为结构质量，工作水深处结构承受的最大等效应力及结构的最大变形量。采用单参数敏感度分析和多参数敏感度分析方法，找出对质量、应力、变形等结构性能指标影响较大的主要参数。

根据滑翔机的关键结构参数对输出参数的响应散点，在ansys中采用Spearman秩相关分析模式进行单参数和多参数敏感度分析，结果如图3所示。

通过对图3结构单参数与多参数敏感度对比柱状图分析可知，对于质量，单参数敏感度与多参数敏感度分析结果极其相近，说明结构参数对质量的响应大小受其他参数变化的影响很小；偏一外倒角，偏二内倒角，偏二外倒角这3个结构参数对结构最大等效应力的单参数敏感度分析与多参数敏感度分析结构差别较大，说明这3个结构参数对结构最大等效应力的响应受结构参数之间的耦合作用显著；同理，H51，偏一外倒角对结构最大变形的响应受结构参数之间的耦合作用较大。

H51，H52，H53，偏一外倒角对结构质量的变化起到主导作用；H51，H53，偏二外倒角是影响结构最大等效应力的最主要因素；H53，偏二外倒角对最大变形起到主导地位。因此通过敏感度分析最终确定结构优化设计的6个参数分别为：H51，H52，H53，偏一外倒角、偏二内倒角、偏二外倒角。

4 滑翔机优化代理模型创建

结构优化时涉及的参数较多，计算机进行计算仿真所消耗的时间较多，计算工作量变得非常巨大，结构优化设计实现起来也存在相当大的难度。因此本文采用代理模型方法来减少计算仿真耗时。Kriging模型对存在非线性的数学模型有很强的适应性与拟合效果，可以解决各项同性及各项异性的问题，本文以该模型方法，利用试验设计获得的设计空间样本点数据创建滑翔机优化代理模型。

用拉丁超立方采样得到的样本点创建Kriging代理模型；然后用ansys响应面自动优化与人工优化联合对Kriging代理模型进行训练[5-7]；最后在设计空间进行10次采样，检测代理模型精度。

4.1 代理模型联合训练

首先用ansys响应面自动细化程序，对Kriging代理模型进行细化，该程序工作原理为：预测误差是一个连续可微的函数，为了找到最佳的候选细化点，细化程序在全部的设计空间内评估Kriging代理模型的预测相对误差，如果新预测点的预测相对误差超过了设定的最大预测相对误差允许值，那么该预测点就成为新的细化点，自动细化程序基于梯度算法不停地迭代，设计空间定位，锁定新的细化点，直到预测点的预测相对误差低于设定的最大相对误差允许值，代理模型拟合达到一定精度，程序收敛。设定程序最大预测相对误差为5%，预测相对误差收敛曲线如图4所示。

图4 预测相对误差收敛曲线

然后利用代理模型人工细化功能对Kriging代理模型进行训练，在设计空间随机选取100个设计点，进行有限元计算，计算结果与Kriging代理模型进行无量纲化操作之后显示在同一坐标系中，选取与代理模型拟合差别较大的设计点作为细化点，进行代理模型的训练更新。

图5 设计点与Kriging代理模型无量纲关系图

4.2 代理模型拟合精度检验

利用ansys在设计空间随机选取10个设计点，进行有限元计算,将这10个点的计算数据与Kriging代理模型上该坐标处的拟合数据进行分析对比，用来检验Kriging代理模型的拟合精度。结果如图5所示。可以看出：采样点与拟合点的数值差别极其微小，在误差允许的范围内，经过训练后的Kriging代理模型达到了非常高的拟合精度，可以代替实际的滑翔机系统响应来进行后续的优化工作。

4.3 代理模型响应面结果

在上述Kriging代理模型确定的基础上，得到质量，应力，变形的响应面结果。图6给出了H52-偏二内倒角响应面结果。

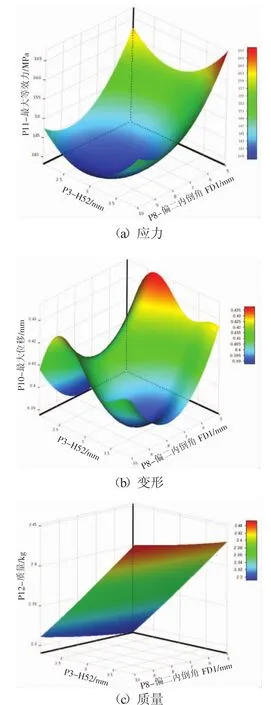
图6 H52-偏二内倒角响应面结果

5 基于NSGA-2的滑翔机结构优化

在上述创建的滑翔机性能代理模型基础上，以质量、等效应力为寻优目标，以结构变形为约束条件，运用NSGA-2多目标遗传算法对滑翔机进行优化设计，目标寻优。

5.1 非支配排序遗传算法

（1）产生种群数量为N的初始种群P0，对个体进行非支配排序，为每个个体确定适应度值，具有相同等级的个体放在一起，2级次之，1级最高，按照规则，将全部个体分配完毕。（2）按照非支配等级高低对初始种群P0进行选择，交叉，变异操作产生种群数量为N的子种群Q0；（3）在每代中，把父代种群Pt和子代种群Qt合并成具有2N个个体的新种群Rt，然后对Rt进行迅速非支配排序，并选择非支配等级高的N个个体直接进入下一代，得到父代种群Pt+1；（4）对新父代种群进行选择，交叉，变异，产生个体数量为N的新子代种群Qt+1，程序运行到t+1代。如此循环，直到进化代数满足收敛条件为止。在多目标优化时，采用非支配解（Pareto）得到优化问题的最优解[8-9]。流程图如图7所示。

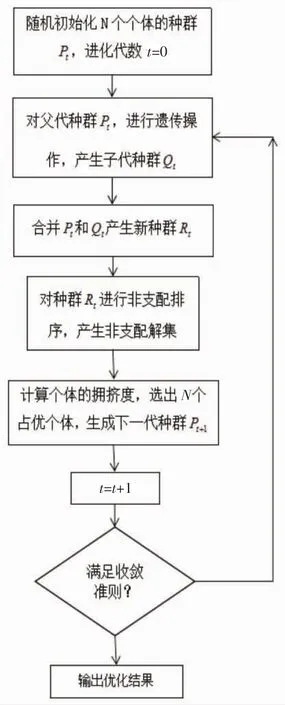
图7 NSGA-2非支配排序遗传算法流程图

5.2 优化结果

以质量最小、等效应力最小且上限为150 MPa为寻优目标，以结构最大变形为0.000 5 m为约束条件进行结构优化设计。优化初始种群数为100，每次迭代种群数为100，最大迭代次数为20，基因突变概率0.01，基因交叉概率0.98，最大容许Pareto百分比为70%，收敛稳定率2%。

在优化到第十代群体，评估完第974个个体时，程序收敛优化结束。图8给出了H52优化时间历程。图9给出了质量-应力pareto前沿面结果。

图8 H52优化时间历程

图9 质量-应力pareto前沿面

滑翔机结构质量与最大等效应力是两个互相牵制的优化目标。每一次的迭代优化都会将这两个目标非支配解（Pareto）前沿面向更优的方向推进，使质量与最大等效应力尽量有同时到达最小值的可能。Pareto前沿面上的解都是多目标优化的非劣解，都是多目标优化所得的最优解，具有相同的地位。优化结束以后程序自动从Pareto前沿面上挑选了一个设计序列作为滑翔机结构优化的最终解，如表1所示。

表1 滑翔机结构优化后参数

通过表1滑翔机优化前初始设计与代理模型优化后实际有限元分析结果对比，可以发现，滑翔机优化后比优化前结构质量减少了5.57%，最大等效应力减少了 14.91%，结构最大变形减少了38.43%。说明了基于代理模型利用非支配排序多目标遗传算法，对滑翔机进行结构优化取得了巨大的优化成效，表明了本文优化方法与优化流程的可行性。

为检验利用代理模型进行优化所得预测结果的精度，按照优化后的结构参数，在ansys workbench进行有限元求解，其结果如图10和表2所示。

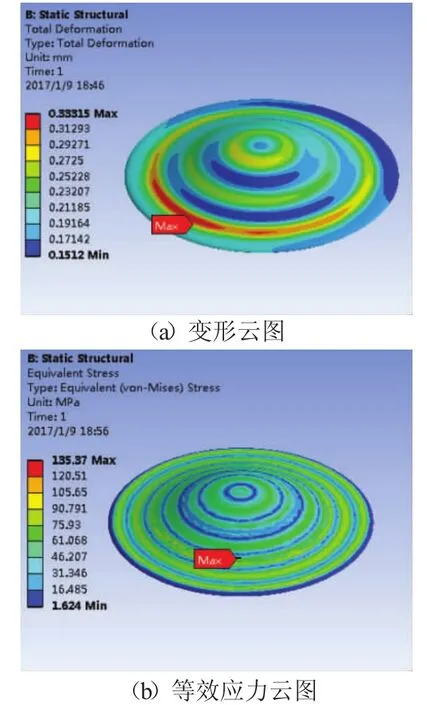
图10 结构优化后结果

通过对代理模型优化后预测结果与有限元分析结果对比表明，代理模型对质量，最大等效应力，最大变形的优化预测结果误差都在5%以内，说明了代理模型优化结果的真实可靠性，也从侧面表明了代理模型对真实响应拟合达到了非常高的精度。

表2 精度对比结果

6 结论

本文提出了一套集计算机仿真、样本试验设计方法、代理模型技术、多目标遗传优化算法于一体的水下滑翔机结构设计优化方案。经过对初始设计与最终设计结果的对比分析，优化后的滑翔机各方面性能均得到了巨大的提升。体现了本文优化思路的可行性，同时也可为其他工程结构的优化工作提供参考。

[1]Jenkins Scott A,Humphreys Douglas E,Sherman Jeff,et al.Underwater Glider SystemStudy[R].Scripps ofOceanographyUC Diego, 2003:7-10.

[2]罗志凡,荣见华,杜海珍.基于遗传算法和梯度算法的一种结构优化混合方法[J].计算机工程与应用学报,2003,38(8):71-73.

[3]易伟建,刘霞.遗传演化结构优化算法[J].工程力学,2004，21(3):66-71.

[4]唐文艳,顾元宪.遗传算法在结构优化中的研究进展[J].力学进展,2002,32(1):26-40.

[5]严云.基于ANSYS参数化设计语言的结构优化设计[J].华东交通大学学报,2004,21(4):52-554.

[6]隋允康,张立新,杜家政.基于响应面方法的朽架截面敏度分析和优化[J].力学季刊，2006,27(1):96-102.

[7]陈国栋.基于代理模型的多目标优化方法及其在车身设计中的应用[D].长沙：湖南大学，2012.

[8]Xu Ruifei,SongWenping,Han Zhonghua.Application ofImproved Kriging-Model-Based Optimization Method in Airfoil Aerodynamic Design[J].Journal ofNorthwestern Polytechnical University，2010,28(4):503-507.

[9]王晓鹏.遗传算法及其在气动优化设计中的应用研究[D].西安：西北工业大学，2000.

Structural Optimization of the Round Dish-Shaped Underwater Gliders Based on the Genetic Algorithm

ZHEN Chun-bo1,LIU Zhao-rui2,WANG Tian-lin1，YING Yang1，YU Peng-yao1
1.College of Traffic Equipment and Ocean Engineering,Dalian Maritime University,Dalian 116026,Liaoning Province,China; 2.School of Naval Architecture,Faculty of Vehicle Engineering and Mechanics,Dalian University of Technology,Dalian 116024, Liaoning Province,China

Considering the structural mass and stress as the objective function,and structural deformation as constraint condition,the structural optimization design of the dish-shaped underwater glider is studied,with the analysis method of single parameter and multi-parameter sensitivity used to select the key structural parameters. The sample points in the design space are selected by using the experimental design method of Latin Hypercube Sampling.Then,the Kriging agent model of the glider structural optimization is established by using the sample point data.After the joint training of the Kriging agent model,the fitting of the model has obtained very high precision.Finally,the second generation of non-dominated sorting genetic algorithm (NSGA-2)is adopted to solve glider optimization problem,and the Pareto front surface optimal solution is obtained.The optimization results show that the structural mass and stress is reduced by 5.57%and 14.91%,respectively.The proposed method is feasible in the structural optimization design of underwater gliders.

underwater glider;structural optimization;sensitivity analysis;Kriging agent model;second generation of non-dominated sorting genetic algorithm

U661.4

A

1003-2029（2017）02-0010-06

10.3969/j.issn.1003-2029.2017.02.002

2017-01-15

国家重点研发计划重点专项资助项目（2016YFC0301500）；国家自然科学基金资助项目（51379025,51609031）；海洋工程国家重点实验室开放基金资助项目（1513）；中央高校基本科研业务费专项资金资助项目（3132016346）；辽宁省博士启动基金资助项目（201601070）

甄春博（1982-），男，博士，讲师，主要研究方向为船舶与海洋结构优化。E-mail：zhenchunbo@163.com

王天霖（1977-），男，博士，教授，主要研究方向为船舶与海洋结构强度分析。E-mail：Tianlin-Wang@163.com