谐波传动短筒柔轮齿形参数优化设计
彭盼道 吴上生 杨琪
(1.华南理工大学机械与汽车工程学院 2.东莞瑞柯电子科技股份有限公司)
谐波传动短筒柔轮齿形参数优化设计
彭盼道1吴上生1杨琪2
(1.华南理工大学机械与汽车工程学院 2.东莞瑞柯电子科技股份有限公司)
以公切线式双圆弧齿廓作为短筒柔轮的齿形,基于ANSYS Workbench14.0有限元软件试验平台,建立波发生器作用下的柔轮有限元接触模型,并应用有限元方法求解柔轮所受应力;采用正交试验方法设计齿形参数不同水平组合的试验方案并进行有限元仿真试验;运用极差分析法对正交试验结果进行分析。仿真与分析结果表明:齿形参数的不同水平组合得到的柔轮最大应力存在较大差别,可以通过对齿形参数进行优化设计降低柔轮应力;齿厚比对柔轮最大应力敏感度最大,是最关键因素。
谐波传动;齿形参数;有限元分析;正交试验
0 引言
20世纪50年代末,谐波齿轮传动问世,与行星齿轮、圆柱齿轮、摆线针齿轮传动相比,谐波齿轮传动具有体积小、回差小、传动精度高、重量轻和传动效率高等优点[1],在机器人领域得到广泛应用。由于机器人领域对谐波齿轮传动的要求越来越高,短筒谐波齿轮传动装置轴向尺寸的减小,使得柔轮倾角增大,柔轮所受应力急剧上升[2]。以往的研究大都集中在通过优化柔轮结构参数降低柔轮应力[3-5],而对柔轮齿形参数的优化设计研究较少。
本文以公切线式双圆弧齿形作为柔轮齿形,建立波发生器作用下的柔轮有限元接触模型,基于有限元分析和正交试验对柔轮齿形参数进行优化设计,以达到降低柔轮应力,提高柔轮疲劳强度的目标。
1 柔轮有限元模型
1.1 柔轮与波发生器设计
以模数为0.3115 mm,柔轮齿数为160个,刚轮齿数为162个,单级传动比为80的短筒谐波减速器为例,对柔轮齿形进行重新设计,公切线式双圆弧齿形如图1所示。齿形参数参照文献[6]推荐值初步选取:齿厚比λ为1.4,凸齿廓ρa半径为0.45 mm,凹齿廓ρf半径为0.45 mm,公切线倾角γ为6°,齿根圆rg半径为0.3 mm。柔轮结构参数按原型机选取。

图1 柔轮双圆弧齿形
波发生器选用余弦凸轮波发生器,该波发生器具有设计简单、计算量小和加工成熟等优点,目前已作为主流波发生器使用。该波发生器由柔性薄壁轴承和余弦凸轮组成。考虑到本文重点分析柔轮应力,因此不对薄壁轴承建模,由余弦凸轮外轮廓向外做等距延伸代替。余弦凸轮外轮廓线极坐标方程为
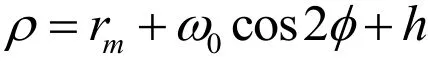
其中,rm为薄壁轴承内径;ω0为柔轮径向变形量;h为薄壁轴承厚度。
1.2 柔轮有限元模型的建立与结果分析
采用Pro/E软件对柔轮和波发生器建立三维模型,然后将其导入ANSYS Workbench14.0有限元分析软件。柔轮材料选用普遍使用的30CrMnSiA,弹性模量为196 GPa,泊松比为0.3;波发生器材料选用45钢。由于两种材料的弹性模量相差不大,因此将柔轮与波发生器的装配模型视作一个“柔体-柔体”的“面-面”接触模型。考虑柔轮内孔与波发生器外轮廓的摩擦,设置摩擦因数为0.08[7],并采用增广拉格朗日法对模型进行求解。因为该接触模型是一个大变形非线性问题[4],所以开启大变形分析和弱弹簧选项,柔轮与输出轴采用螺栓连接,并在柔轮凸缘底面施加固定约束,划分网格后生成的柔轮有限元模型如图2所示。

图2 柔轮有限元模型
对上述有限元模型求解,得到柔轮的等效应力云图如图3所示。由图3可知,柔轮最大应力位于长轴附近齿圈后端靠近筒体处,齿根处存在明显的应力集中现象,这与文献[8-9]的试验与理论分析一致,表明了有限元模型的准确性。

图3 柔轮应力云图
2 柔轮齿形参数优化设计
2.1 正交试验设计
正交试验设计是利用“正交表”进行合理安排、科学分析各试验因素的有效数理统计方法[10]。它在试验因素的全部水平组合中,挑选部分有代表性的水平组合进行试验。通过对试验结果分析,了解全面试验情况,找出最优水平组合。
本次试验以有限元分析中的柔轮所受最大应力作为评价指标,分析齿厚比λ、公切线倾角γ、凸齿廓半径ρa、凹齿廓半径ρf和齿根圆半径rg的大小变化对柔轮最大应力的影响规律。以上齿形参数的取值范围主要根据参考文献[6]选取,以等差数列形式给出每个齿形参数的4个水平,所以因素水平表采用五因素四水平,如表1所示。
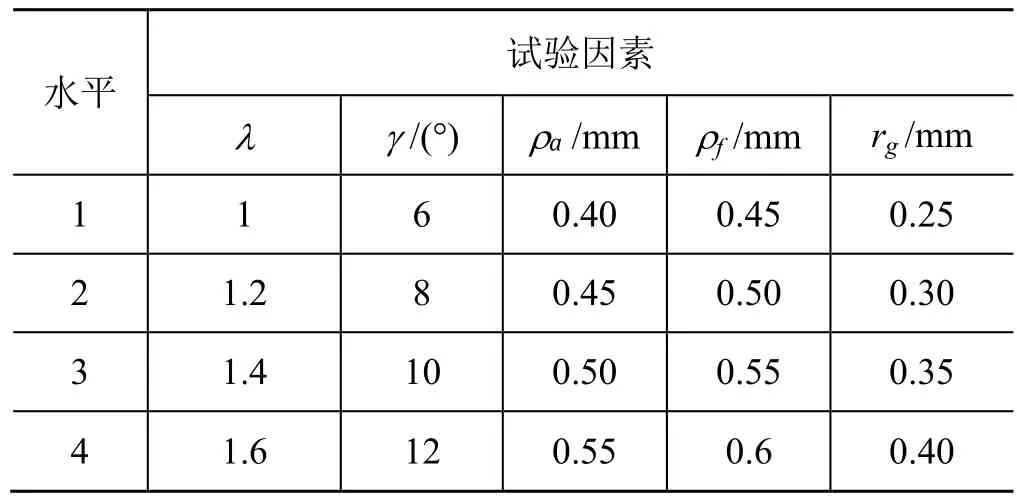
表1 五因素四水平表
根据表1,本文选用L16(45)型正交表,用正交表安排试验共有16组,相比将每个齿形参数的各水平全部参与组合产生1024次试验,正交试验大大减少了试验次数。
2.2 结果分析
根据正交表规定的试验方案确定每组方案的各齿形参数数值,用Pro/E软件建立每组试验的三维模型,然后将模型导入ANSYS Workbench14.0仿真平台,分别对每组试验进行有限元分析,得出每组试验柔轮所受最大应力值,试验方案和试验结果如表2所示。
由表2可知,不同试验方案的结果存在较大差异。试验中最优水平组合是第15组试验,其柔轮最大应力值比第4组试验的结果小123.03 MPa。由此可知,柔轮齿形优化设计对降低柔轮应力,提高柔轮寿命具有重要意义。
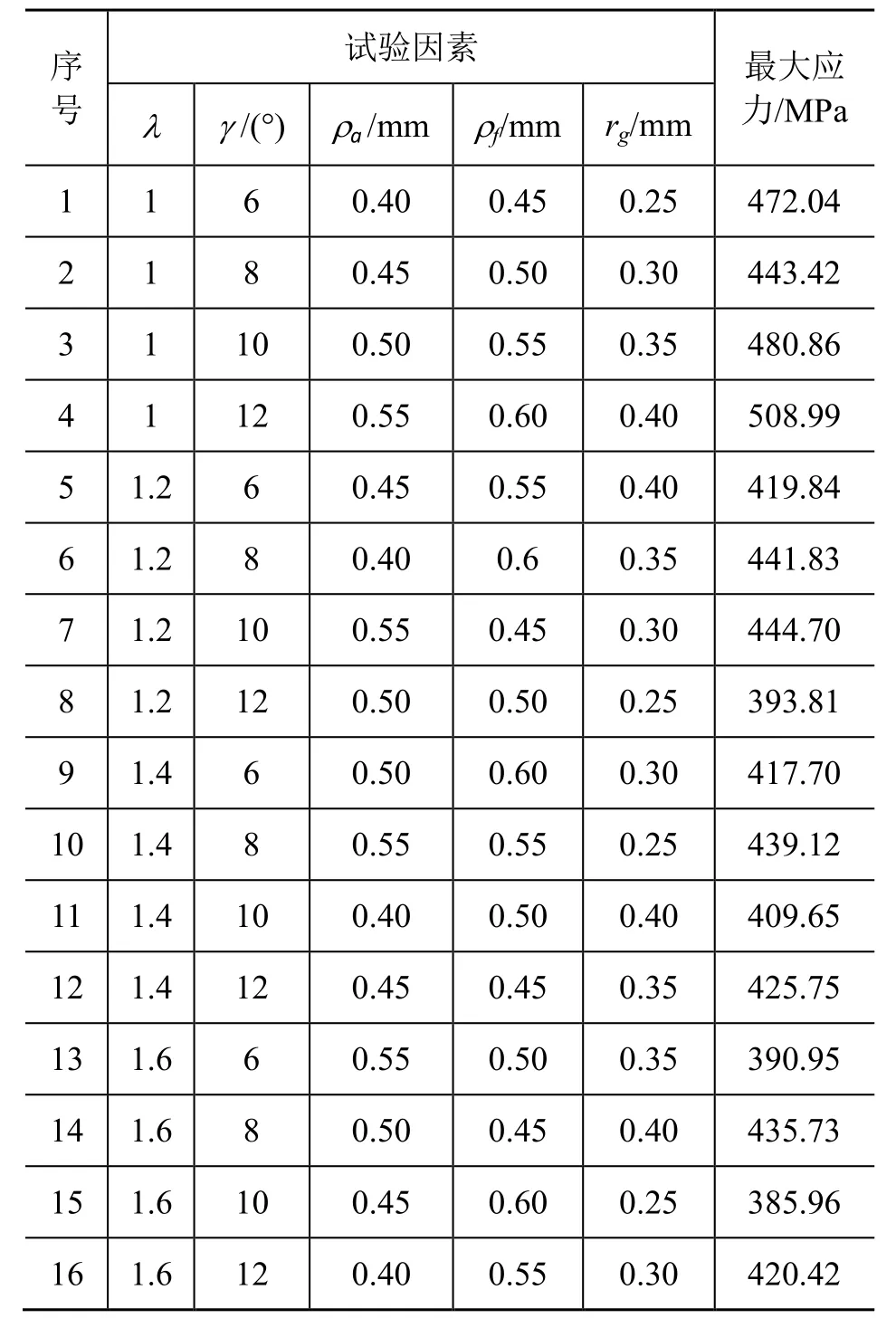
表2 试验方案与结果
为得到理论最优水平组合和各因素对柔轮最大应力敏感度大小,采用极差分析法对以上正交试验结果进行分析。极差分析结果如表3所示,为各水平结果求和的平均值,R为极差。
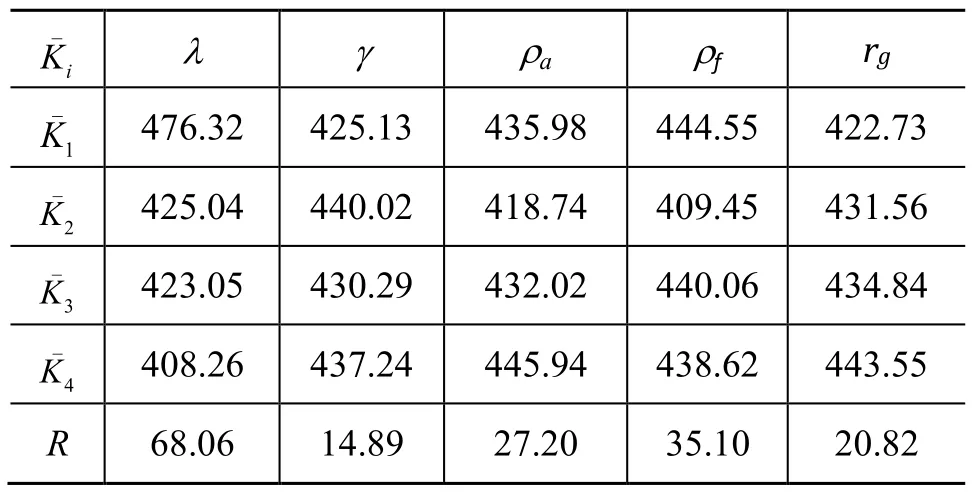
表3 极差分析结果
由各因素的极差R可知,齿厚比λ对柔轮最大应力的敏感度最大,是最关键因素;公切线倾角γ对柔轮最大应力的敏感度最小,为次要因素。因素的敏感度由大到小依次为齿厚比λ、凹齿廓半径ρf、凸齿廓半径ρa、齿根圆半径rg、公切线倾角γ。在以后的齿形优化设计过程中,可选取敏感度较大的因素作为优化设计变量,忽略敏感度较小的因素,以提高优化设计效率。
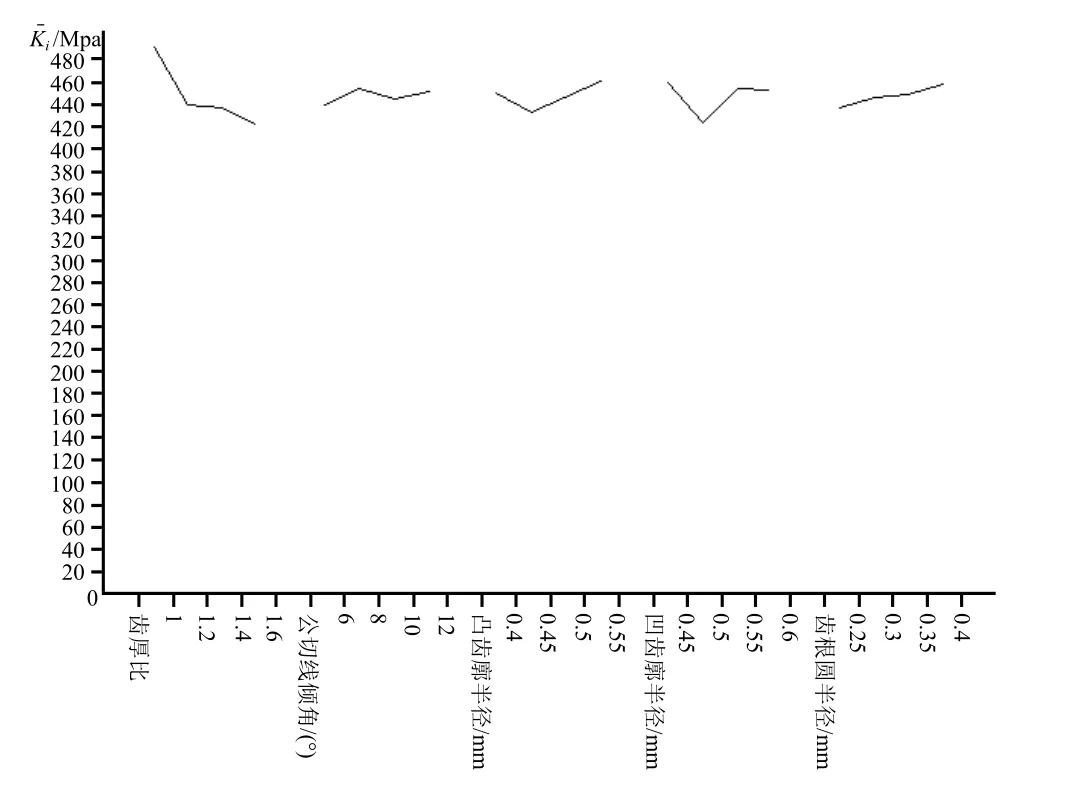
图4 趋势图
为直观显示柔轮最大应力随各因素水平变化的趋势,以各因素的水平作为横坐标,柔轮最大应力作为纵坐标,趋势图如图4所示。由图4可看出,各因素水平因子的变化引起柔轮最大应力上升、下降的幅度差异很大。随着齿厚比的增大,柔轮最大应力急剧减小后趋于平缓减小,因此设计齿厚比较大的柔轮齿形对降低柔轮应力具有显著效果。齿根圆半径的增大使柔轮应力缓慢增大,其他3个因素水平的增大对柔轮最大应力变化有升有降,需要做更多水平的试验以确定影响规律。
3 结论
柔轮最大应力位于长轴附近齿圈后端靠近筒体处,齿根处存在明显的应力集中现象,是柔轮产生疲劳破坏的主要原因。
齿形参数的不同水平组合产生的柔轮最大应力存在较大差别,可以通过优化齿形参数降低柔轮应力。
齿厚比对柔轮最大应力敏感度最大,是最关键因素,因此在工程设计中应设计齿槽较宽的双圆弧齿廓短筒柔轮。
[1] 范又功,曹炳和.谐波齿轮传动技术手册[M].北京:国防工业出版社,1995:1-2.
[2] 吴伟国,于鹏飞,侯月阳.短筒柔轮谐波齿轮传动新设计新工艺与实验[J].哈尔滨工业大学学报,2014,46(1):40-46.
[3] 董惠敏,李德举,齐书学.基于正交试验和有限元分析的谐波传动柔轮杯体结构优化[J].机械传动,2013,37(1):34-38.
[4] 高海波,李志刚,邓宗全.基于ANSYS的杯形柔轮结构参数对柔轮应力的敏感度分析[J].机械工程学报,2010,46(5):1-7.
[5] 王新,周璇,李成群.谐波减速器柔轮结构优化设计[J].机械设计与制造,2013(11):67-69.
[6] 辛洪兵.具有双圆弧齿廓的谐波齿轮传动:中国, 200610112755.6[P].2008-03-05.
[7] 于鹏飞.机器人用短筒柔轮谐波减速器研制与性能测试[D].哈尔滨:哈尔滨工业大学,2012:16-18.
[8] 沈允文,叶庆泰.谐波齿轮传动的理论与设计[M].北京:机械工业出版社,1985:181-182.
[9] 辛洪兵.柔轮齿圈应力的有限元分析[J].机械科学与技术, 2003,22(4):558-559.
[10] 李志西,杜双奎.试验优化设计与统计分析[M].北京:科学出版社,2010:143.
Tooth Profile Parameters Optimization Design of the Short Flexspline in Harmonic Drive
Peng Pandao1Wu Shangsheng1Yang Qi2
(1.School of Mechanical and Automotive Engineering, South China University of Technology 2.Dongguan Richtek Electronics Co., Ltd.)
Double-arc tooth profile with common tangent is used as the tooth profile of the short flexspline, based on ANSYS Workbench14.0 finite element software test platform, the contact model of the flexspline under the action of wave generator is established, utilizing the finite element method solve the stress of flexspline, the experiment scheme of different level combination of tooth profile parameters was designed by orthogonal test and the finite element simulation experiment is carried out, the results of orthogonal test were analyzed by the range analysis method. Simulation and analysis results show that: The maximum stress of the flexspline is different in different level combinations of the tooth profile parameters, it is possible to reduce the stress of the flexspline by optimizing the design of tooth profile parameters; The ratio of tooth thickness is maximum to sensitivity of flexspline maximum stress and is the most critical factor.
Harmonic Drive; Tooth Profile Parameters; Finite Element Analysis; Orthogonal Test
彭盼道,男,1991年生,硕士生,主要研究方向:机械设计及理论。E-mail: pengpandao@163.com
吴上生,男,1963年生,博士,教授,主要研究方向:精密机械设计与制造。E-mail: shshwu@scut.edu.cn

