基于轨迹规划的飞机发动机数字化安装技术研究

盛贤君,王 杰,姜 涛,刘睿智

（1. 大连理工大学电气工程学院,大连 116024；2. 大连理工大学信息与通信工程学院,大连116024)

航空发动机作为为飞机提供动力、推动航空器前进的装置,是飞机性能、可靠性和成本的决定性因素[1]。由于发动机存在重量大、体积大、外形结构复杂和安装间隙狭小等问题,所以使得飞机发动机的安装工作比较困难。

飞机大部件的数字化装配技术在欧美等发达国家发展较早，他们开发了先进的计算机虚拟装配[2]、可视化装配路径规划[3]和柔性数字化装配[4]等技术，已向由自动化装配工装、模块化加工单元和数字化定位等组成的自动化装配系统发展[5]。国内飞机装配中人工装配仍然占据主要地位， 与国外相比有较大的差距[6]，而且西方发达国家长期以来一直对我国进行技术封锁，我国航空发动机的安装普遍采用简单的机械和液压装置进行人工的手动安装方法[7]，很难克服上述困难。因此，有必要研究一种自动化的飞机发动机数字化安装技术。

由于发动机不是一个标准的圆柱体，而且飞机短舱内有一定的障碍物，所以发动机轨迹规划的优劣直接决定着其是否能够安装成功，数字化安装的核心问题就是发动机的轨迹规划。本文对安装系统的调姿平台进行了运动学分析，阐述了基于位置的视觉伺服控制原理，对标准的发动机安装轨迹进行齐次坐标变换，得到发动机安装的离线轨迹规划。在发动机安装过程中，根据发动机位姿测量算法得到的偏差，实时修正轨迹，进行在线的轨迹规划。自动安装过程中，通过逆向运动学分析，将轨迹点转化为各轴电机的目标位置，控制各坐标轴联动完成发动机在笛卡尔空间的移动。作为一种特殊的移动机器人，该数字化安装系统具有灵活性好、自动化程度高等特点。

1 数控调姿平台的运动学分析

1.1 数字化安装系统的机械结构

为了满足发动机安装过程所需的机动性和多姿态等性能要求，设计了带有电动装置和液压装置的五轴联动数字化安装系统。其机械结构如图1所示。

数控调姿平台的位姿由平移机构、升降俯仰机构和转台机构的联动来决定。两个平移机构实现X与Y轴方向的移动，升降俯仰机构实现Z轴方向的移动与B轴的旋转运动，转台机构实现C轴的旋转运动。飞机发动机通过夹具固定在数控调姿平台上，发动机的姿态即为数控调姿平台的姿态。

1.2 发动机调姿平台的运动学分析

为了能够精确地控制发动机按照规划的轨迹运动，需要对数控调姿平台进行运动学分析。由于调姿平台需要满足承重大、调姿灵活等要求，升降俯仰机构设计为双“人”字形结构，其侧视结构如图2所示。通过两个滑块B1和B2的左右移动使左、右长支链改变倾角，上方动平台的两个支点（转动副）可以分别垂直上下移动，实现调姿平台的Z轴移动以及B轴转动。升降俯仰机构下方的定平台固定在平移机构2内部，其随平移机构2的移动沿着X轴方向运动。

动平台两支点A1、A2的间距为S，左、右两长支链长度均为2L，左、右两短支链长度均为L，并且短支链一端通过转动副连接在长支链的中点处。两个滑块通过两个伺服电机控制，分别在OB1XB1、OB2XB2坐标轴上移动。两电机回零时，两滑块所在的位置分别为OB1、OB2，此时A1、A2处于它们垂直移动范围的最低点（即定义为Z轴的原点）。左、右短支链在定平台的支点（转动副）与OB1、OB2的距离均为B0。

通过各结构的几何关系得到升降俯仰机构的运动学正解：

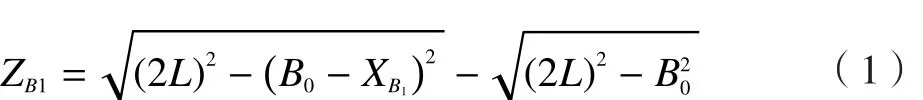
图1 数字化安装系统的机械结构Fig.1 Mechanical structure of digital installation system

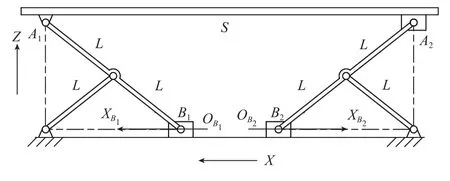
图2 升降俯仰机构侧视结构图Fig.2 Side structure of lift and tilt mechanism

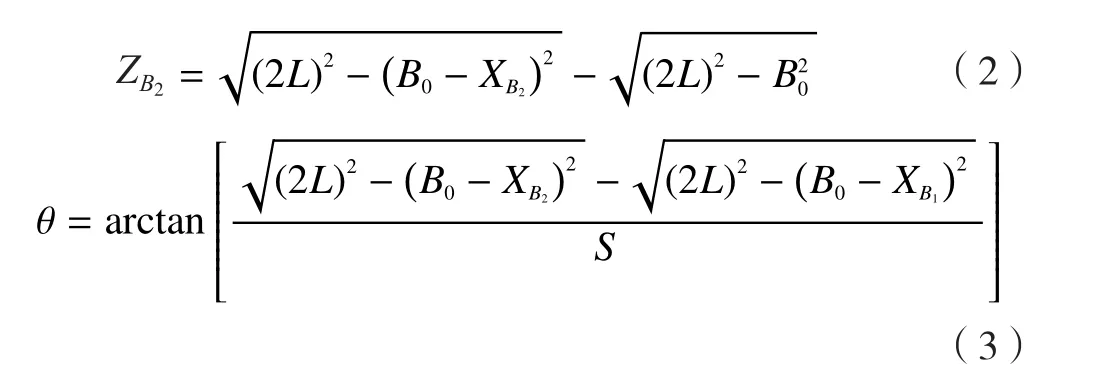
其中，ZB1、ZB2分别是当两滑块坐标为XB1、XB2时的支点A1与A2的Z轴坐标；θ为此时调姿平台在B轴方向的旋转角度。

若已知支点A1与A2的Z轴坐标ZB1、ZB2或者调姿平台的转角θ，那么可以得到运动学的逆解：

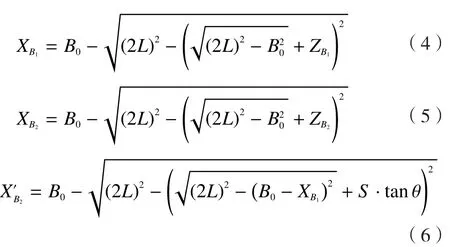
其中，X'B2为调整滑块B2使调姿平台在B轴的转角为θ时B2滑块的坐标，这一过程滑块B1不动。

从上述公式可以看出，尽管升降俯仰机构的左右支链在结构上是对称的，但由于滑块的平移与支点的升降是非线性关系，就使得对Z轴和B轴进行增量式控制时，要考虑调姿平台当前Z轴和B轴的位置，即要实现下一时刻的位姿，需根据前一时刻的位姿来计算控制量。调姿平台在X、Y和C轴上的运动分别通过平移机构和转台机构来完成，它们的运动距离或转角与各自的电机编码器脉冲都呈线性关系。

2 发动机安装的离线轨迹规划

要寻求由起点到终点的无碰撞路径，需要同时考虑发动机位置和姿态的变化。尽管发动机和飞机短舱的尺寸都可以由设计图纸得到，发动机在短舱内的标准安装路径可通过计算机辅助分析而得出，但是由于不能保证安装系统与飞机短舱的位置相对正，所以应根据安装系统的初始位置对标准安装路径进行坐标变换，生成系统实际控制的发动机轨迹。

假设安装系统、飞机短舱和摄像机的位置俯视图如图3所示。坐标系A为安装系统所控制的各轴所建立的坐标系，原点为各轴回零时数控调姿平台的位置。坐标系B建立在飞机短舱上，其OBXB轴与短舱轴心重合，OBYB轴与水平面平行。坐标系C定义在摄像机上，其为摄像机的光心坐标系。B与C各自3个坐标轴分别平行，且OBXB与OCXC在同一直线上。为了便于摄像机识别，发动机前端固定一个圆形标靶。根据发动机尺寸，将标准安装路径转化为标靶中心的轨迹并离散化，其包括了在B坐标系中的位置信息BP和姿态信息RB，即：

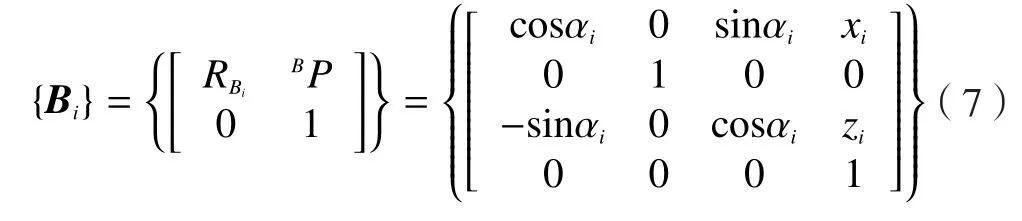
其中，αi为标靶在B坐标系中B轴方向的转角；（xi，0，zi）为标靶中心在B坐标系的位置坐标。发动机的位姿即等同于标靶的位姿。为了获取短舱相对于安装系统的位置，应对发动机的初始位置进行校准，通过调整安装系统的调姿平台，当摄像机测量出发动机前端中心点与B坐标系原点重合并且发动机对正短舱口时，安装系统的各轴坐标值为B坐标系在A中的位姿，也就是坐标系B与A的变换矩阵：

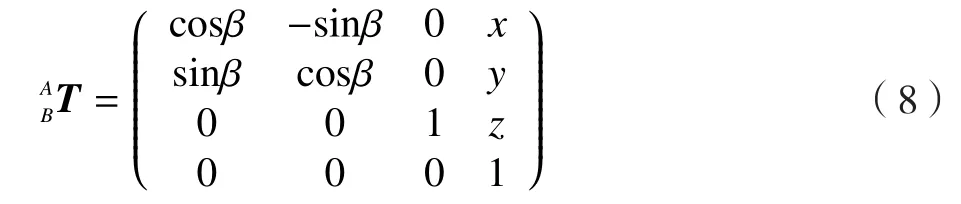
其中，β为此时CA轴坐标值；(x，y，z)为此时XA、YA和ZA轴坐标值。通过对{Bi}齐次坐标变换得到坐标系A中发动机的轨迹：

{Ai}为发动机在A坐标系下的轨迹点，即安装系统所需控制的离线轨迹。

根据运动学逆解，将离线轨迹转变为各伺服电机所需的脉冲控制量，对各轴进行插补运动控制，便能实现发动机在离线轨迹规划下的安装。

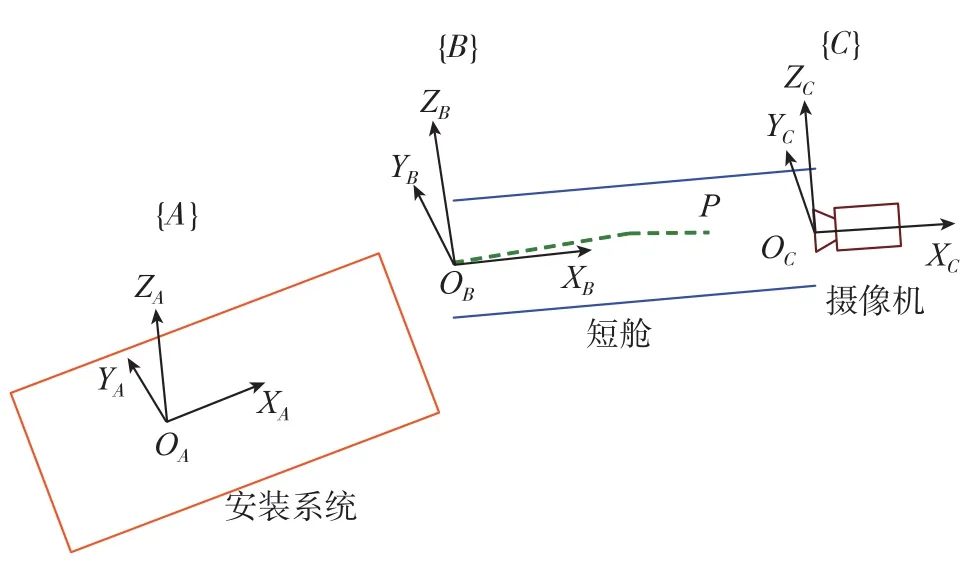
图3 安装系统、飞机短舱和摄像机的位置俯视图Fig.3 Platform of system, nacelle and camera

3 发动机安装的在线轨迹规划

离线轨迹规划的精确性取决于校准时发动机与短舱的对正程度，校准后发动机便沿着校准时的方向运动。由于校准时发动机与摄像机的距离较远，有效图像信息比例较少，会影响测量的准确度。而发动机安装轨迹的长度大约为3000mm，这就使得即使0.1°的校准偏差也会对发动机的最终位置带来约5mm的偏差，很难达到理想的安装效果，故应对离线轨迹进行修正。本文采用了基于位置的视觉伺服控制，通过摄像机测量发动机前端标靶的偏差，在发动机安装过程中对离线轨迹进行实时修正，进而消除校准偏差带来的影响。

3.1 基于位置的视觉伺服控制

基于位置的视觉伺服控制是根据摄像机测量的目标位置，控制目标的运动以达到调整目标位姿的目的[8]。本文运用单目摄像机，构建Eye-to-Hand系统，控制原理如图4所示。系统由3个闭环构成，外环为图像空间的位置环，各个坐标轴采用位置环和速度环控制，其内环为速度环，外环为位置环。视觉测量由图像采集、特征提取、像素矩阵复原和发动机位姿计算等部分构成。在发动机按照离线轨迹安装的过程中，校准偏差反馈不断对离线轨迹进行修正，得到发动机将要运动的新轨迹。

3.2 发动机位姿的测量

电荷耦合器件（Charge Coupled Device， CCD）作为摄像机的感光元件，在每个小的像点都会产生与光强成比例的电荷量，按照一定顺序读取各像素点聚集的电荷量就可以构成图像的像素表示[9]。电荷信息转换成数字信号，生成各像素的灰度信息。由于本文中的标靶具有旋转对称的特点，将其图像进行径向展开变换，使旋转对称纹理转换成平移对称纹理，而变换后的图像灰度矩阵具有低秩的特点。

为了操作简单、移动灵活，安装系统采用单目摄像机。摄像机放置于短舱末端，摄像机的光轴与短舱的中心轴在同一直线上，如图4所示。根据摄像机的成像平面坐标系、图像坐标系以及光心坐标系之间的关系模型，得到光心坐标系中的点与摄像机中对应像点之间的坐标转换关系：

图4 基于位置的视觉伺服控制Fig.4 Visual servo control based on position

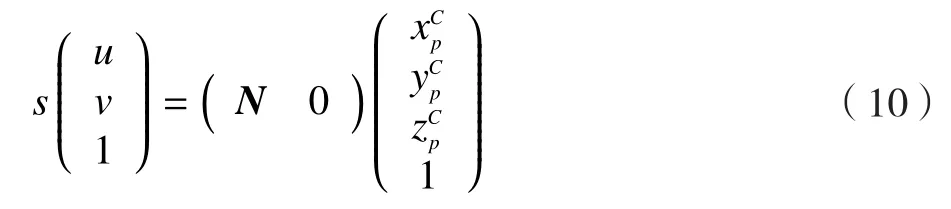
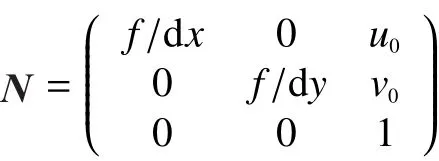
通常摄像机拍摄的图像是倾斜的，而且是受到噪声干扰的，本文中标靶的图像纹理可以表示为：

其中，I为倾斜图像矩阵；τ由相机的内部和外部参数组成，包括焦距f、光心坐标系与世界坐标系关系的旋转矩阵和位置矩阵，τ使I变换为理想对正图像；F{.}为径向展开变换；为理想正对图像的径向展开变换矩阵，其为低秩的；稀疏矩阵E为噪声带来的误差矩阵。

是低秩的，E是稀疏的，求相机参数可以转换成低秩矩阵复原问题，将式（11）作为约束方程，可以表示为以下优化关系式：

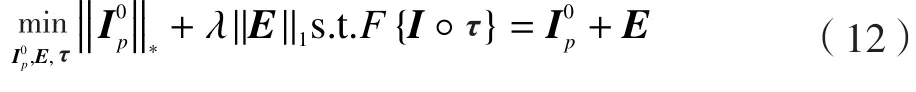
其中，λ>0，用以折中低秩部分与稀疏误差部分。此优化关系反映的问题是，纹理矩阵的秩达到最小并且误差矩阵尽量稀疏时，求取I0p、E和τ的值。将约束方程线性化，利用增广拉格朗日乘子法[10]进行迭代求解式（12），得到包含相机的内、外部参数的变换矩阵τ。根据公式（10），得到任一时刻标靶中心在光心坐标系中的坐标。如果将世界坐标系的X轴建立在标靶中心轴上，那么所求τ中的光心坐标系和世界坐标系的旋转矩阵就表示了标靶相对短舱的角度偏转量。

3.3 离线轨迹的修正

若发动机按照离线轨迹自动移动，依照图像灰度匹配的快速算法[11]，实时对摄像机得到的图像进行处理，并计算发动机的位置和姿态相对于短舱的偏差ε，当ε大于一定的阈值时，将得到的位姿偏差矩阵εT补偿到离线轨迹中，得到修正后的轨迹，再按照修正后的轨迹进行安装，如果再出现偏差大于阈值的情况，则再次对轨迹进行修正。第n次修正的轨迹可以表示为：

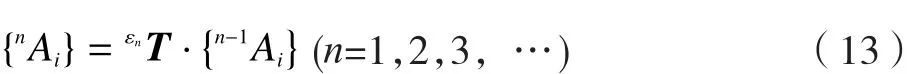
其中，εnT为第n次修正量；{0Ai}为没有修正过的离线轨迹，直到发动机达到最终的安装位置，在线轨迹规划结束。

4 发动机安装试验

根据所设计的系统控制原理，搭建了基于双CPU的开放式数字化安装系统。在上位机的VS2008和Matlab中实现离线轨迹规划和发动机的实时位置测量，对下位机中的运动控制卡编写程序，实现发动机在在线轨迹规划下的自动安装。根据发动机和短舱的实际尺寸，构建出二者的等效模型，进行模拟装配试验，如图5所示。

应用本文提出的轨迹规划方法，对发动机进行模拟安装。由于上位机对位姿偏差的计算需要一定的时间，故自动安装过程应有周期性的短暂中断，使下位机能够得到计算结果并进行轨迹修正。

整个自动安装过程，记录下安装系统各轴坐标值，最终安装系统在Y轴和Z轴方向的轨迹如图6、7所示。其中红色点序列为离线的轨迹规划，蓝色点序列为在线轨迹规划，绿色点序列为发动机实时位置偏差。可以看出，当发动机的位置偏差大于一定阈值时，系统会对Y轴或Z轴方向进行轨迹修正。在线修正后的轨迹作为发动机的实际安装路径，如图8所示。

经过多次模拟安装试验，证实了轨迹规划下安装发动机的可行性。同样应用上述数字化安装系统在某飞机上进行了发动机安装试验，相比传统安装方法在精度和效率等方面都有了明显的改进。

图5 发动机模拟安装试验Fig.5 Analog experiment of engine installation

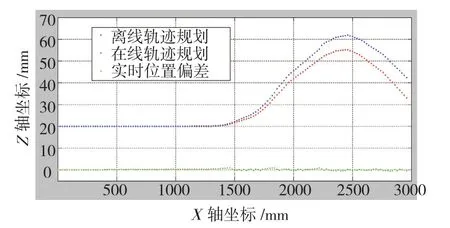
图6 轨迹规划在X-Z平面上的映射Fig.6 Planned trajectory mapping upon X-Z

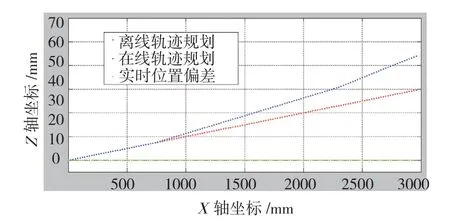
图7 规划轨迹在X-Y平面上的映射Fig.7 Planned trajectory mapping upon X-Y

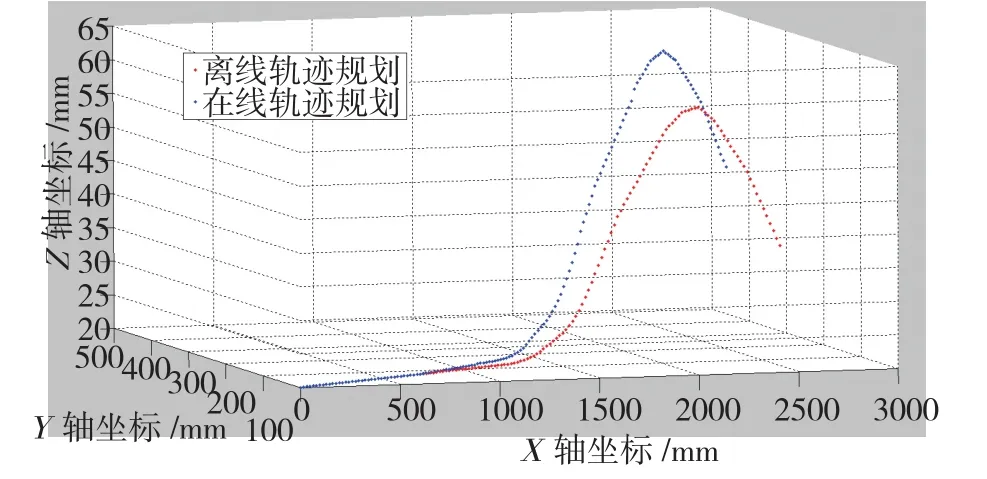
图8 发动机安装的轨迹Fig.8 Trajectory of engine installation

5 结论

针对飞机发动机传统安装方法的效率低、精度差等问题，本文提出了基于视觉的发动机数字化安装系统设计方案。对系统的数控调姿平台进行了运动学分析，给出了飞机发动机安装的离线轨迹和在线轨迹的规划方法，其中离线轨迹是自动安装的基础，但由于校准过程带来的偏差，发动机很难按照离线轨迹完成安装，这就需要实时对离线轨迹进行在线修正，将在线规划的轨迹作为发动机的安装路径。通过数字化安装系统对两种轨迹规划方法进行了验证，实现了飞机发动机的自动化安装。试验结果表明，这种新型的数字化安装技术能够稳定、高效地完成飞机发动机的安装工作，与传统方法相比，提高了安装精度、缩短了工作周期、减小了人力成本，具有一定的应用前景。

[1] 陈予恕,张华彪. 航空发动机整机动力学研究进展与展望[J].航空学报, 2011, 32(8): 1371-1391.

CHEN Yushu, ZHANG Huabiao. Review and prospect on the research of dynamics of complete aero-engine systems[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(8): 1371-1391.

[2] MING C L，ELMARAGHY H A ，NEE A Y C, et al. CAD model based virtual assembly simulation, planning and training[J]. CIRP Annals-Manufacturing Technology, 2013, 62(2): 799-822.

[3] HASSAN S, YOON J. Haptic assisted aircraft optimal assembly path planning scheme based on swarming and artificial potential field approach[J]. Advances in Engineering Software, 2014, 69(3): 18-25.

[4] MUELANER J E, MARTIN O C, MAROPOULOS P G. Achieving low cost and high quality aero structure assembly through integrated digital metrology systems[J]. Procedia CIRP, 2013, 7(5): 688-693.

[5] 郭洪杰. 大型飞机柔性装配技术[J]. 航空制造技术, 2010(5):52-54.

GUO Hongjie. Flexible assembly technology for large commercial aircraft[J]. Aeronautical Manufacturing Technology, 2010(5): 52-54.

[6] 许国康. 大型飞机自动化装配技术[J]. 航空学报, 2008,29(3): 734-740.

XU Guokang. Automatic assembly technology for large aircraft[J].Acta Aeronautica et Astronautica Sinica, 2008, 29(3): 734-740.

[7] 雷海峰. 航空发动机数控安装架车的设计及结构分析[D].大连:大连理工大学, 2013.

LEI Haifeng. Aero-engine NC installation vehicle design and structure analysis[D]. Dalian: Dalian University of Technology, 2013.

[8] 邱联奎. 基于机械手的视觉伺服控制及其应用研究[D]. 合肥:中国科学技术大学, 2006.

QIU Liankui. Research on robot manipulator visual servo control and applications[D]. Hefei: University of Science and Technology of China,2006.

[9] 谭民,徐德,侯增广,等. 先进机器人控制[M]. 北京:高等教育出版社, 2007.

TAN Min, XU De, HOU Zengguang, et al. Advanced robot control[M].Beijing: Higher Education Press, 2007.

[10] 阚超. 基于Moreau包络函数的复合优化增广拉格朗日对偶及算法[D]. 哈尔滨:哈尔滨工业大学, 2014.

KAN Chao. Augmented lagrangian dual and algorithm for composite optimization based on the Moreau envelope[D]. Harbin: Harbin Institute of Technology, 2014.

[11] 刘锦峰. 图像模版匹配快速算法研究[D]. 长沙:中南大学,2007.

LIU Jinfeng. Study on fast image template matching algorithm[D].Changsha: Central South University, 2007.