基于Mathematica的宝塔菜收获机二阶平面铲倾角的优化设计

李金川，郑毅敏，尚 欣，慕 松，史鑫鹏

(1.宁夏大学机械工程学院， 宁夏 银川 750021；2.宁夏大学大学生就业创业指导服务中心， 宁夏 银川 750021)

基于Mathematica的宝塔菜收获机二阶平面铲倾角的优化设计

李金川1，郑毅敏2，尚 欣1，慕 松1，史鑫鹏1

(1.宁夏大学机械工程学院， 宁夏 银川 750021；2.宁夏大学大学生就业创业指导服务中心， 宁夏 银川 750021)

为了进一步提高宝塔菜收获机二阶平面铲的碎土能力，基于Mathematica对宝塔菜收获机二阶平面铲倾角进行了优化设计。设计中建立了二阶平面铲多目标优化模型，在该模型中，引入了土壤破碎模型及挖掘铲阻力模型，借助虚拟倾角的概念，运用Mathematica软件对其进行求解，得到了一个一阶铲面倾角为20.44°，二阶铲面倾角为43.64°，一阶铲面高度为0.12 m，虚拟铲面倾角为30.53°的理论上铲面受力最小、土壤有效剪切力最大的挖掘铲模型，并从理论角度和软件仿真角度对优化前后二阶铲进行分析对比，发现优化后的挖掘铲较现有二阶铲的铲面长度、受到的挖掘阻力、最大变形量、所受最大应力及应变均减小，达到了优化效果。该模型为高碎土能力挖掘铲的设计提供了理论支持和改进方向。

宝塔菜收获机；二阶平面铲；倾角；多目标优化设计；应变分析

宝塔菜属唇形科多年生宿根植物，地下根茎呈现螺旋状塔形。其肉质脆嫩，易与土壤粘连，在机械收获过程中，很容易损伤果实表皮。在宝塔菜收获过程中，挖掘铲的结构型式和几何参数对挖掘阻力的大小影响很大。目前国内外设计的固定式挖掘铲，按照铲面形状分为三角平面铲、二阶平面铲、曲面铲、栅条铲等[1-2]。

目前国内外对宝塔菜收获机的研究很少，市场上暂无投入生产的收获机械，而其他根茎类作物(如马铃薯、花生等)收获机的挖掘铲大多数为三角平面铲，出土量多时易产生大土块，发生壅土现象，从而使机具动力消耗急剧增大。而基于宝塔菜自身特点，三角平面铲达不到充分碎土的效果。曲面铲虽然有较好的碎土能力，但造价较高，设计过程较为繁琐[3]。栅条铲适用于大型根茎类作物收获[4]。而二阶平面铲在三角平面铲的基础上增加了一个倾角，使土壤发生二次剪切，提高了碎土能力；在制造成本方面，二阶铲采用压力加工，折弯模的制造成本比用于制造曲面铲的模具成本低。

综合考虑入土性能、碎土能力及制造成本等方面因素，在宝塔菜联合收获机的设计中，挖掘铲选用了二阶平面铲，该二阶铲是在倾角为30°的平面铲上增加了一个较小的倾角平面，在样机试验过程中，挖掘铲的碎土性能并未得到明显改善。

为了进一步提高二阶平面铲的碎土能力，本文引入土壤破碎模型及挖掘铲力学模型，建立了多目标函数，对二阶平面铲的一阶倾角、二阶倾角和一阶倾角高度进行了优化设计，并将优化结果与现有二阶平面铲的结构进行了分析对比。设计过程中，直接对二阶平面铲倾角进行优化设计难度较大，因此借助了平面铲虚拟倾角的概念[5]。

1 引入力学模型

1.1 土壤破碎模型

以虚拟倾角为δ的三角平面铲为研究对象，参考已有的土壤破碎模型[6]，即

T′=Q-T

T=τb(H-h′)/sinβ

式中，T′为有效剪切力(N)；T为剪力(N)；b为铲面宽度(m)；τ为剪切面上的剪应力，可用τ=C+σtanφ计算，其中，C为土壤内聚力因数，σ为正应力，φ为内摩擦角(正应力在这里为0)；H为铲的工作深度(m)；β剪切面与水平面的夹角；Q为压紧力(N)；L为铲的平移距离(m)；h′为挖掘铲行进L距离后土壤上升高度；q为压缩单位体积的土壤作用力(N·m-3)；δ为铲面倾角；φ为土壤与铲面的外摩擦角。

1.2 挖掘铲力学模型

以三角平面铲为研究对象，参考已有的挖掘铲—牵引阻力模型[7]，即

其中，力学模型中其他参数公式如下：

土壤沿铲尾伸出的距离：

式中，γ为土壤容重(kg·m-3)；L1为土壤沿铲尖伸出的距离(m)；L2为土壤沿铲尾伸出的距离(m)；L0为铲面总长度(m)；d1为土壤厚度(m)；d为挖掘深度(m)；h为铲面高度(m)；v0为挖掘铲的工作速度。

各参数名称、类型及大小如表1所示。

2 二阶铲铲面倾角的优化设计

2.1 二阶铲截面形状设计

根据图1中虚拟平面铲铲面倾角、虚拟平面铲铲面长度与一阶铲面倾角、二阶铲面倾角和一阶铲面高度的几何关系，建立数学模型：

图1 二阶铲截面参数示意图

Fig.1DiagramofSecond-ordershovelsection

(1)

其中，

(2)

推导出虚拟倾角与一阶铲面倾角、二阶铲面倾角和一阶铲面高度的关系：

表1 初始计算参数

(3)

式中，δ为虚拟铲面倾角；α1为一阶曲面铲铲面倾角；α2为二阶曲面铲铲面倾角；h为铲面高度或提升高度，h=0.3 m；h1为一阶铲面高度；L0为虚拟平面铲铲面长度。

2.2.1 优化数学模型 在工作深度一定的条件下，对虚拟平面铲进行优化设计，应选择设计变量为铲面倾角δ，即：

X=[x1]=[δ]

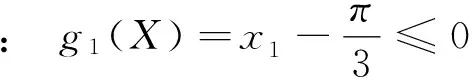
选择两个力学模型为目标函数，即：

(1) 虚拟铲面阻力最小的目标函数：

令f1(X)=F，则有：

(2) 土壤有效剪切力的负数最小的目标函数：

令f2(X)=-T，则有：

minf2(X)=-[1/2Lh′bq-τb(H-h′)/sinβ]

2.2.2 数学模型的求解 采用统一目标法中的线性加权和法进行优化。线性加权和法是将多目标函数构成一个综合目标函数，把一个要最小化的函数F(x)规定为有关性质的结合。在算法的运算中，各个分目标函数的重要程度不同，因此需要综合考虑其影响。通常根据多目标优化问题式中各个目标函数的重要程度，对应地选择一组权系数[8]。其多目标优化的评价函数为：

2.4.2 术后随访 TURBT术后应规律随访，膀胱镜检为NMIBC患者随访的金标准，检查过程中发现异常均应取活检。推荐术后3个月时行第1次膀胱镜检，高危患者前2年每3个月1次，第3年开始每6个月1次，第5年开始每年1次直至终身。低危患者如第1次镜检阴性，可于术后1年行第2次镜检，之后每年1次直至第5年。中危患者介于两者之间。随访过程中一旦出现复发，治疗后的随访方案按上述方案重新开始。

式中，Wi(i=1,2,…,l)为权系数，且Wi≥0；fi(X)(i=1,2,…,l)为分目标函数；D为约束可行域。

运用Mathematica软件中NMinimize函数(约束最优化中数值非线性全局最优化函数)数值化求解单目标函数的最优值。NMinimize中有多种优化方法，包括直接搜索法、差分进化法、模拟退火算法、随机搜索法等。NMinimize根据问题的类型选择优化方法，如果有整数变量，或者如果目标函数的头部不是一个数值函数的话，则采用差分进化算法，对于其他非线性类型的问题，则采用直接搜索法，但是如果直接搜索法运行不佳的话，就会切换到差分进化算法[9]。

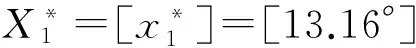
图2 设计变量与目标函数1的关系

Fig.2 Relationship between design variables

and objective function 1

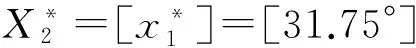
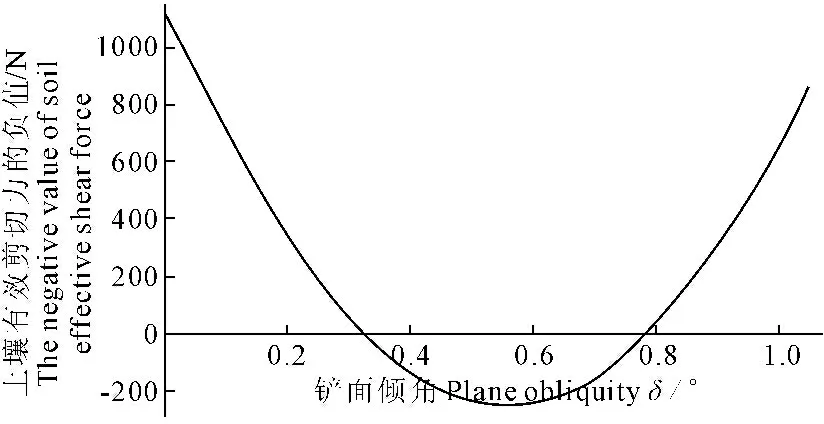
图3 设计变量与目标函数2的关系

Fig.3 Relationship between design variables and objective function 2

所以，求得权系数：

则，多目标优化的评价函数为：

再次利用Mathematica软件对综合目标函数进行优化计算，得到自变量的最优值：

设计变量与评价函数之间的关系如图4。

优化出虚拟倾角为30.53°，该角度可作为后续二阶平面铲倾角优化的约束条件。

2.3 二阶铲面倾角的多目标优化设计

平面铲的铲面倾角和铲面长度直接影响铲面的碎土性能，为了能够得到最佳的铲面倾角和铲面长度，就需要保证在提高碎土性能的前提下对其进行优化设计。

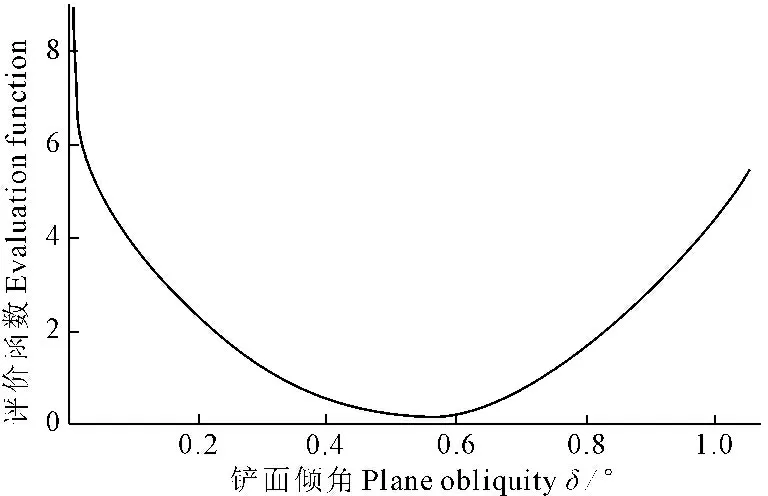
图4 设计变量与评价函数的关系

Fig.4Relationshipbetweendesignvariablesandevaluationfunction

引入2.1节中的式(1)～式(3)，将虚拟倾角替换成与一阶倾角、二阶倾角、一阶铲面高度相关的表达式，来完成对铲面倾角的优化设计。

2.3.1 优化数学模型 在工作深度一定的条件下，对二阶平面铲进行优化设计，应选择设计变量为一阶铲面倾角α1、二阶铲面倾角α2和一阶铲面高度h1，即：

X=[x1，x2，x3]T=[α1，α2，h1]T

根据图1可知，一阶倾角α1必须小于虚拟倾角δ，二阶倾角必须大于虚拟倾角δ，一阶铲面高度h1必须小于铲面高度(提升高度)h，则约束条件为：

g1(X)=x1-30.53°≤0

g2(X)=x2-30.53°≥0

g3(X)=x3-0.3≤0

目标函数的选择与2.2节中虚拟倾角优化设计相同，即虚拟铲面阻力最小的目标函数、土壤有效剪切力的负数最小的目标函数。

2.3.2 数学模型的求解 选用线性加权和法，评价函数同第2节，求得权系数后，再运用Mathematica软件中NMinimize函数来数值化求解。

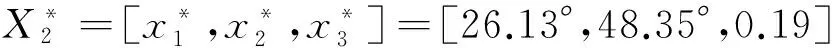
所以，求得权系数：

则，多目标优化的评价函数为：

再次利用Mathematica软件对综合目标函数进行优化计算，得到自变量的最优值：

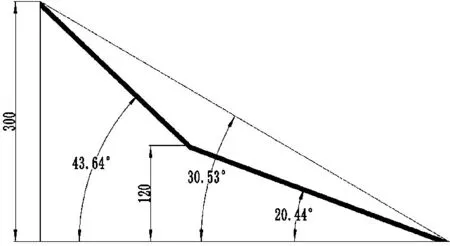
图5 二阶平面铲截面参数

Fig.5Sectionalparametersofsecond-orderflatshovel

最终优化得到一阶铲面倾角α1=20.44°，二阶铲面倾角α2=43.64°，一阶铲面高度h1=0.12 m，虚拟铲面倾角δ=30.53°，如图5。

3 优化前后对比分析

3.1 优化前后铲面结构对比

由于挖掘深度的要求，改进前后不变的参数为铲面高度(提升高度)，均为300 mm，改进前、后的二阶铲截面几何参数如表2。

运用SolidWorks对优化前后的挖掘铲三维建模，两三维模型对比如图6。

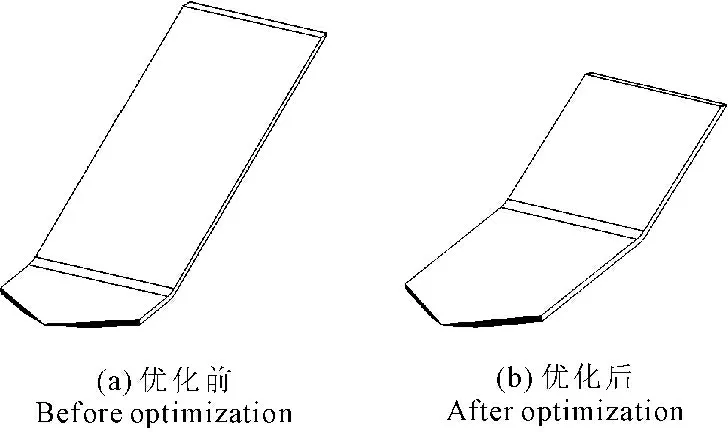
图6 优化前后三维模型对比

Fig.6 The 3D model contrast before and after optimization

通过优化设计，二阶铲的铲面长度明显减少，铲面虚拟倾角也更接近于根茎类收获机挖掘铲的一般倾角(30°)[10]。

3.2 优化前后虚拟铲面受力结果对比

优化前后，直接改变的参数为铲面倾角，间接改变的参数有铲面面积，在对比优化前后的挖掘阻力、法向载荷及铲面所受摩擦力时，需要改变铲面倾角和铲面面积的大小，根据挖掘铲力学模型来数值求解[7]。优化前后虚拟倾角平面铲的铲面受力对比如表3所示。

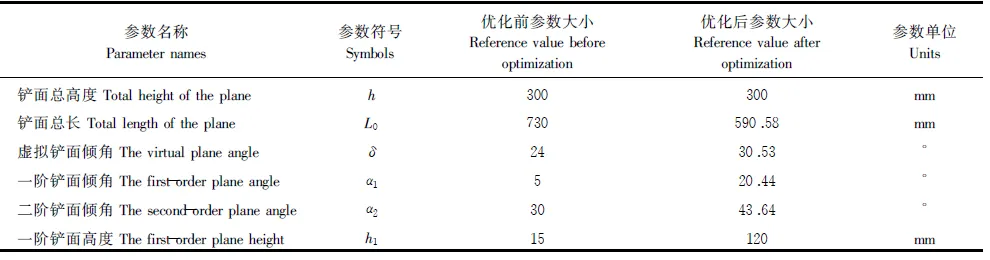
表2 优化前后二阶铲截面几何参数对比表

表3 优化前后虚拟铲面受力结果对比

根据对比分析，优化后的挖掘铲较现有铲所受到的挖掘阻力(或机具牵引力)明显减小，达到了优化效果。

3.3 静力学分析

运用ANSYS软件对优化前后的挖掘铲进行有限元静力学分析。铲面受力包括土壤作用的法向载荷、土壤对挖掘铲作用的摩擦力及因土壤粘性产生的附着力。因为优化前后各个铲面倾角的大小、铲面面积均不同，所以需要根据两参数分别求出各铲面的受力。各铲面受力情况如表4所示。

表4 优化前后各铲面受力情况

将三维模型其导入ANSYS软件中，单元类型选择Solid185，弹性模量为2.06×1011N·m-1，泊松比为0.3，然后进行网格划分、添加边界条件及施加载荷。在宝塔菜收获机中，采用组合铲，每个单铲的两侧固定于机架上，所以边界条件限制两侧面的自由度。载荷按照表4的数据施加，法向载荷为压强(Pa)，摩擦力和附着力为节点力(N)。添加节点力时，需要将摩擦力和附着力的合力分解到X、Y方向上，并通过输入“*GET，aaa，NODE，0，COUNT”命令计算出该面上的节点个数，选择整个面的节点，加载平均节点力。

在输出应力及应变云图时，分别选择“von Mises stress”及“von Mises elastic strain”，von Mises是一种屈服准则，屈服准则的值通常叫作等效应力，它遵循材料力学第四强度理论(形状改变比能理论)。优化前后的应力及应变云图结果如图7～8所示。

优化后的二阶铲受力后的变形量、所受最大应力及应变均减小，分析结果见表5。

图7 优化前后铲面应力云图对比

Fig.7 The stress nephogram contrast of two shovels

图8 优化前后铲面应变云图对比

Fig.8 The strain nephogram contrast of two shovels

表5 有限元分析结果对比

4 结 论

1) 通过在二阶平面铲多目标优化模型中引入了土壤破碎模型及挖掘铲阻力模型，借助虚拟倾角的概念，运用Mathematica软件对其进行求解得到了一个一阶铲面倾角为20.44°，二阶铲面倾角为43.64°，一阶铲面高度为0.12 m，虚拟铲面倾角为30.53°的理论上铲面受力最小、土壤有效剪切力最大的挖掘铲模型。

2) 从理论角度和软件仿真角度对优化前后二阶铲进行了分析对比，发现优化后的挖掘铲较现有二阶铲的铲面长度、受到的挖掘阻力、最大变形量、所受最大应力及应变均减小，达到了优化效果。该模型为高碎土能力挖掘铲的设计提供了理论支持和改进方向。

[1] 杨然兵，李国莹，尚书旗，等.机械化挖掘收获部件发展现状与展望[J].农机化研究，2008，(9)：5-9.

[2] 胡志超，彭宝良，尹文庆，等.多功能根茎类作物联合收获机设计与实验[J].农业机械学报，2008，39(8)：58-61.

[3] 罗彤娥，吴建民，孙 伟，等.2种马铃薯挖掘铲的对比分析[J].甘肃农业大学学报，2011，46(3)：121-125.

[4] Yang Ranbing, Shang Shuqi. Design and test of multifunctional curved-surface shovel in digging harvest[J]. Transactions of the Chinese Society of Agricultural Engineering，2012，(S2)：47-52.

[5] 关意昭，张周强，黄范辉，等.木薯收获机二阶曲面铲的有限元静力学分析[J].农机化研究，2012，(10)：42-49.

[6] 吉尔WR，范德伯奇GE.耕作和牵引土壤动力学[M].耕作和牵引土壤动力学翻译组，译.北京：中国农业机械出版社，1983:102-160.

[7] 邓伟刚，孙 宏，王春光.马铃薯挖掘铲工作阻力计算与分析[J].农机化研究，2014，(10):71-74.

[8] 孙靖民，梁迎春.机械优化设计[M].北京：机械工业出版社，2006.

[9] 徐安农.科学计算引论：基于Mathematica的数值分析[M].北京：机械工业出版社，2010.

[10] 李宝筏.农业机械学[M].北京：中国农业出版社，2003.

Optimization of the angle of artichoke harvester's second-order flat shovel based on mathematica

LI Jin-chuan1, ZHENG Yi-min2, SHANG Xin1, MU Song1, SHI Xin-peng1

(1.CollegeofMechanicalEngineering,NingxiaUniversity,Yinchuan,Ningxia750021,China；2.ServiceCenterofCareerandEmploymentGuidance,NingxiaUniversity,Yinchuan,Ningxia750021,China)

In order to further improve Chinese artichoke harvester’s second-order flat shovel, a multi-objective optimization model of second-order flat shovel was established. A soil breaking model and a resistance model of digging shovel were introduced in this model. With the help of the concept of virtual angle and Mathematica, the model was established with the first-order plane angle being 20.44°, the second-order plane angle being 43.64°, the first-order plane height being 0.12 m, and the virtual plane angle being 30.53°. This theoretically digging shovel model had the minimum force and the maximal effective soil shear. Comparison and analysis of the two second-order shovel from the perspective of theory and software simulation were made. The results showed that the shovel length, digging resistance, the maximum deformation, and stain of optimized digging shovel were decreasing, which indicated this optimal design was satisfactory. This optimal model provided a theoretical support and enlightenment for the design of digging shovel with high soil-breaking ability.

artichoke harvester；second order flat shovel；angle；multi-objective optimal design；strain analysis

1000-7601(2017)02-0282-07

10.7606/j.issn.1000-7601.2017.02.45

2015-12-26基金项目：宁夏回族自治区科技支撑计划项目“宝塔菜联合收获机的研制”(413-0224)

李金川(1992—)，男，山东夏津人，硕士研究生，主要研究方向为智能农业装备。 E-mail:ljcnxu@163.com。

郑毅敏(1964—)，男，浙江黄岩人，教授，主要从事农业机械化研究。 E-mail:XJKZym@nXu.edu.cn。

S225.7+9

A